Трансцендентное уравнение это простыми словами

Видео:Математика для всех. Алексей Савватеев. Лекция 6.9. Алгебраические и трансцендентные числаСкачать

Постановка задачи. Основные определения из алгебры нелинейных и трансцендентных уравнений.

Уравнение, не сводящееся к алгебраическому уравнению с помощью алгебраических преобразований, называется трансцендентным уравнением.

Простейшими трансцендентными уравнениями являются показательные, логарифмические и тригонометрические уравнения.

Под алгебраическими преобразованиями уравнения F=0 понимают следующие преобразования:

1) прибавление к обеим частям уравнения одного и того же алгебраического выражения;

2) умножение обеих частей уравнения на одно и то же алгебраическое выражение;

3) возведение обеих частей уравнения в рациональную степень.

Алгебраическим уравнением называется уравнение вида

где Р_n – многочлен n-ой степени от одной или нескольких переменных.

Трансцендентная функция– функция, не являющаяся алгебраической функцией.

Трансцендентное уравнение – уравнение, содержащее неизвестное в аргументе некоторой трансцендентной функции, например: .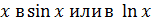

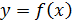
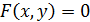
Алгебраическая функция – : 1. Функция от одного переменного , удовлетворяющая алгебраическому уравнению , где F – полином от двух переменных.

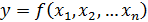
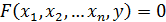
2.Функция от n переменных , удовлетворяющая алгебраическому уравнению , где F – неприводимый полином от n+1 переменных.

Рассмотрим нелинейное уравнение одной независимой переменной x,

f(x)=0, x 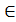[a,b], (1)

где f(x) – любая нелинейная или трансцендентная функция, например, .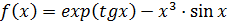

Нахождение корней уравнения (1) производится в два этапа:

1. Отделение корней – это нахождение таких интервалов по аргументу x, внутри каждого из которых существует только один корень уравнения (1).

2. Уточнение корней заключается в применении некоторого итерационного метода, в результате которого корень уравнения (1) может быть получен с любой наперед заданной точностью ε.

Видео:Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Уравнения. Системы уравнений

Цель лекции: познакомиться с основными возможностями, принципами и средствами Mathematica для решения алгебраических и дифференциальных уравнений, систем уравнений.

8.0. Введение

Доступ к множеству оригинальных алгоритмов при помощи встроенных функций, широчайшие возможности символьного и графического представления результатов делают Mathematica эффективным инструментом аналитического и численного решения уравнений. В данной лекции мы познакомимся с основными функциями Mathematica, применяемыми для нахождения решений алгебраических, трансцендентных и дифференциальных уравнений, а также систем уравнений. В этом нам помогут книги Е. М. Воробьёва [1] и А.Н. Прокопени [5].

8.1. Нахождение символьных решений алгебраических и трансцендентных уравнений

Наиболее часто используемая функция для решений уравнений — Solve . Она позволяет находить решения полиномиальных уравнений вплоть до чётвёртого порядка, некоторых полиномиальных уравнений высших порядков, а также неполиномииальных уравнений (А. Н. Прокопеня и А. В. Чичурин [5, с. 28]). В простейшем случае для решения одного уравнения lhs==rhs ( lhs и rhs — левая и правая части уравнения, соответственно) с одной неизвестной var функция задаётся в виде Solve[lhs==rhs,var] (пример In[1] на рис. 8.1). Корни уравнения выдаются в виде вложенного списка правил замены в виде подстановок (см. Out[1] )

Для того чтобы решить при помощи этой функции систему уравнений, нужно задать оба обязательных аргумента в виде списков уравнений и переменных, т. е., записать функцию как Solve[,] . Уравнения также можно отделять друг от друга логическим оператором && (логическим умножением).

В примере In[2] на рис. 8.1 мы решили систему уравнений. Обратим внимание на то, в каком виде мы получаем корни системы. В Out[2] мы получаем вложенный список , элементами которого являются одномерные списки. Каждый одномерный список в качестве элементов содержит пару корней системы уравнений.

Для того чтобы была возможность в дальнейшем производить манипуляции с корнями уравнения или системы уравнений, следует от вложенного списка правил преобразований перейти к одномерному списку корней уравнения или системы уравнений. Делается это при помощи уже известного нам оператора » /. «. Так в примере In[3] на рис. 8.1 мы присвоили выражению xroots список корней системы уравнений в In[2] для переменной x .

Обратиться к конкретному корню уравнения или системы уравнений теперь можно, пользуясь навыками работы со списками. Так в примере In[4] на рис. 8.1 мы вывели на экран первое правило подстановки из списка, полученного в результате решения уравнения In[2] , а в In[5] — второй в списке набор корней этого же уравнения с учётом преобразования In[3] .

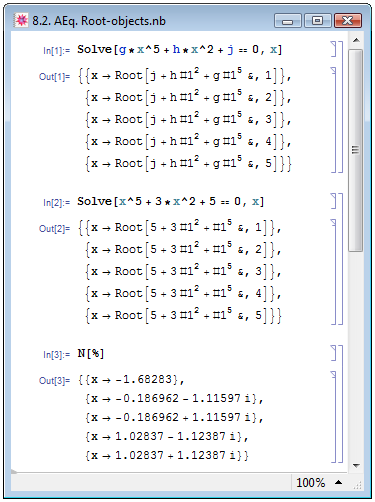
Если Mathematica не может представить решение полиномиального уравнения в аналитическом виде, например, в случае, если полином в уравнении имеет степень выше четвёртой, то корни таких уравнений представляются программой при помощи Root -объектов (А. Н. Прокопеня и А. В. Чичурин [5, с. 29]). Такой объект в виде Root[f,k] представляет точное значении корня с номером k полиномиального уравнения f[x]==0 . Пример полученных в таком виде решений — Out[1] на рис. 8.2.

В примере In[1] на рис. 8.2 мы находили решение уравнения, заданного в общем виде. Если все коэффициенты уравнения имеют численные значения (как в примере In[2] ), то получить численные значения корней не составляет труда при помощи функции N — пример In[3] .

В предыдущих примерах обсуждались возможности функции Solve применительно к алгебраическим уравнениям. В примере In[1] на рис. 8.3 мы попробовали решить с её помощью трансцендентное уравнение 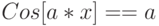относительно переменной x . Понятие трансцендентного уравнения в Mathematica ничем не отличается от его понятия в математике: Трансцендентное уравнение — уравнение, не являющееся алгебраическим. Обычно это уравнения, содержащие показательные, логарифмические, тригонометрические, обратные тригонометрические и др. функции.

Как мы видим в Out[1] на рис. 8.3, для нашего трансцендентного уравнения Mathematica также сумела найти корень. Мы знаем, что на самом деле такое уравнение имеет бесконечное число корней, отличающихся на . Знает это и Mathematica: поэтому она выдаёт сообщение о том, что помимо найденного ей могут существовать и другие корни уравнения.

Однако в ряде случаев Mathematica оказывается бессильной найти корни трансцендентного уравнения в символьном виде. Тогда она выдаёт сообщение, в котором честно признаётся в своём бессилии и рекомендует попробовать решить уравнение неалгебраическими (численными) методами (см. пример In[2] на рис. 8.3).

Видео:РЕШАЕМ ДИОФАНТОВОЕ УРАВНЕНИЕ | ПРОСТЫМИ СЛОВАМИСкачать

Что такое Трансцендентность

Видео:Трансцендентные числа [1] // Алексей БеловСкачать

Значение трансцендентности

Трансцендентность (от лат. transcendens – превосходящий, выходящий за пределы) — это всё то, что выходит за пределы познания мира через органы чувств; предмет метафизического и религиозного учения.

Антонимы слова трансцендентный — эмпирический, познаваемый, опытный. Синонимы слова трансцендентный — непознаваемый, запредельный.

Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

Различия между трансцендентальный и трансцендентный

Трансцендентальное — по мнению философа Иммануила Канта, это касается предшествующих форм изучения (до опыта), не относится к предмету или содержанию познания. Например: время, пространство, причинность.

Трансцендентным, по мнению Канта, было всё то, что выходило за грань познания опытом.

Например, в системе Канта трансцендентными называются «вещи в себе» (или «вещь сама по себе»). Так Иммануил Кант обозначал вещи непознаваемыми — они существуют сами по себе, независимо от того, чем они являются для нас.

Трансцендентальным Кант называет всё то, что относится к априорным условиям опыта, вдобавок те знания, которые могут выйти из этого опыта.

В своих трудах Кант называет трансцендентальным всякое познание, которое появляется больше из изучения видов познания предметов, чем самих предметов. И это познание возможно лишь до опыта.

Трансцендентально — всё то, что является частью опыта и делает возможным его эмпирическое познание. Трансцендентно — всё то, что выходит за рамки опыта.

Трансцендентальное — это как противоположность трансцендентному.

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Трансцендентные и имманентные причины и действия

В схоластике (средневековая христианская философия, которая стремилась обосновать религиозные догматы) различали имманентные и трансцендентные причины и действия. Имманентные случаются в самих объектах, трансцендентные существуют за гранью их реального бытия.

Трансцендентность и имманентность Бога

На первый взгляд трансцендентность и имманентность противоречат друг другу. Однако, если вдуматься в оба понятия и идею Бога, можно понять смысл этого выражения.

Трансцендентное — это то, что находится за пределами восприятия, независимо от Вселенной. И если сравнивать, это совершенно от нас отличается. В противовес этому существует понятие «имманентный Бог» — это тот, который существует внутри нас, внутри Вселенной и т. д. Что означает, что Он является частью нашего существования.

Видео:Трансцендентные числа. Пояснение.Скачать

Что такое трансценденция?

Трансценденция — это философский термин, который означает «переступать через сущее»; это основная структура субъективности. Трансценденция превосходит всё, что означает, что она не имеет сущности.

Видео:06.05.2021. Решения трансцендентных уравнений в элементарных функциях.Скачать

Трансцендентное состояние

В медитации существует такое понятие как «Трансцендентное состояние». Это когда сознание выходит за рамки нормальных трёх состояний сознания, которые известны нам в обычной жизни (бодрствование, сон со снами, крепкий сон).

Эти считаются уровнями возбуждённого состояния, и когда человек их трансцендирует, его разум переходит стесняющие его границы. Таким образом он проникает на более углублённые, безмятежные и мощные ступени познания.

Видео:Классический способ решения Диофантовых уравнений ➜ Решите уравнение в целых числах ➜ 13x-7y=6Скачать

Трансцендентность в математике

Это понятие также существует в математике.

Трансцендентное уравнение

Уравнения, которые не попадают в категорию алгебраических уравнений называются трансцендентными уравнениями. Это уравнение, где есть трансцендентные функции. Например: tan x – e× = 0.

Трансцендентная функция

Это элементарная функция (аналитическая), которая не является алгебраической функцией. Например, функция sin(x).

Трансцендентное число

Это (возможно, комплексное) число, которое не является корнем любого целочисленного полинома. Это означает, что это число не является алгебраическим (ни в какой степени).

Любое трансцендентное число также является иррациональным (т. к. рациональное число — это алгебраическое число в первой степени, а этого быть не может).

Примеры трансцендентных чисел включают π (Пи) и e (число Эйлера).

Узнайте также, что такое Экспонента и Число Пи.

🌟 Видео

Число e - 2,718. Объяснение математического смысла.Скачать

Как распознать талантливого математикаСкачать

Как решать Диофантовы уравнения ➜ Решите уравнение в целых числах 4x+5y=6Скачать

Математика. Линейные диофантовы уравнения с двумя неизвестными. Центр онлайн-обучения «Фоксфорд»Скачать

Урок 455. Уравнение ШрёдингераСкачать

Химические уравнения // Как Составлять Уравнения Реакций // Химия 9 классСкачать

РЕАКЦИИ ИОННОГО ОБМЕНА, ИОННОЕ УРАВНЕНИЕ - Урок Химия 9 класс / Подготовка к ЕГЭ по ХимииСкачать

Как расставлять коэффициенты в уравнении реакции? Химия с нуля 7-8 класс | TutorOnlineСкачать

Как решать Диофантовы уравнения ★ 9x+13y=-1 ★ Решите уравнение в целых числахСкачать

Уравнение из МФТИ Эпичный косякСкачать