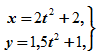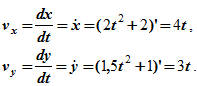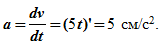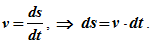Траектория точки по двум уравнениям онлайн (2 видео)

Содержание

Траектория движения
Определение и основные понятия траектории движения
Уравнение траектории движения
Обратимость движения
Параметры траектории движения
Примеры задач с решением
iSopromat.ru
Задача
Решение
Расчет траектории
Расчет скорости
Расчет ускорения
Определение пути
Уравнение прямой по двум точкам
🔥 Видео

Видео:Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

Траектория движения

Видео:Кинематика точки Задание К1Скачать

Определение и основные понятия траектории движения

Во многих задачах интерес представлю не только перемещения материальных точек в пространстве, но и траектории их движения.

Линию, которую описывает частица при своем движении, называется траекторией движения.

В зависимости от формы траектории механическое движение можно разделить на:

прямолинейное движение, траекторией движения точки в этом случае является прямая линия;
и криволинейное перемещение (траектория — кривая линия).

Форма траектории зависит от выбора системы отсчета. В разных системах отсчета траектории могут быть представлены разными линиями, могут быть прямыми и кривыми.

При движении точки с постоянным ускорением, которое описывает уравнение:

Видео:Траектория и уравнения движения точки. Задача 1Скачать

Уравнение траектории движения

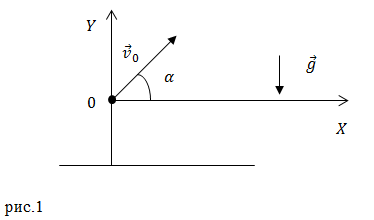
Рассмотрим свободное движение тела около поверхности Земли. Начало координат разместим в точке бросания тела (рис.1). Оси координат направим так, как изображено на рис.1.

Тогда уравнение движения тела (1) в проекциях на координатные оси декартовой системы координат принимает вид системы из двух уравнений:

Для того чтобы получить уравнение траектории движения тела ($y=y(x)$) следует исключить время движения тела из уравнений (2) и (3). Выразим из уравнения (2) $t$ и подставим его в выражение (3), получим:

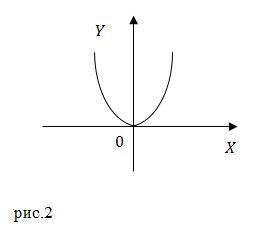
Выражение (4) это уравнение параболы, проходящей через начало координат. Ее верви направлены вниз, так как коэффициент при $x^2$ меньше нуля.

Вершина этой параболы находится в точке с координатами:

Найти координаты вершины траектории можно при помощи известных правил исследования функций на экстремум. Так, положение максимума функции $y(x)$ определяют, приравнивая к нулю первую производную ($frac$) от нее по $x$.

Видео:Уравнение прямой по двум точкамСкачать

Обратимость движения

Из представления о траектории можно конкретизировать смысл обратимости механического движения.

Пусть частица движется в силовом поле таком, что ее ускорение в любой точке обладает определенной величиной, не зависящей от скорости. Как будет двигаться эта частица, если, в какой то точке ее траектории направление скорости заменить противоположным? С точки зрения математики это эквивалентно замене $t $ на $-t$ для всех уравнений. Уравнение траектории время не содержит, получается, что частица будет перемещаться «вспять» по той же самой траектории. При этом отрезки времени между любыми точками траектории будут одинаковы при прямом и обратном движении. Всякой точке траектории ставится в соответствие определенное значение величины скорости независимо от направления движения по данной траектории. Данные свойства наглядны в колебательных движениях маятника.

Все сказанное выше справедливо тогда, когда можно пренебречь любым сопротивлением движению. Обратимость движения существует, когда выполняется закон сохранения механической энергии.

Видео:К1 Определение скорости и ускорения точки по заданным уравнениям ее движенияСкачать

Параметры траектории движения

Положение точек системы отсчета можно определять при помощи разных способов. В соответствии с этими способами описывают и движение точки или тела:

Координатная форма описания движения. Выбирается система координат, в ней положение точки характеризуют тремя координатами (в трехмерном пространстве). Это могут быть координаты $x_1=x,x_2=y,x_3=z$, в декартовой системе координат. $x_1=rho ,x_2=varphi ,x_3= z$ в цилиндрической системе и т.д. При перемещении точки координаты являются функциями времени. Описать движение точки — это значит указать эти функции: [x_1=x_1left(tright);; x_2=x_2left(tright);; x_3=x_3left(tright)left(6right).]
При описании движения в векторной форме положение материальной точки задает радиус-вектор ($overline$) по отношению к точке, которую принимают начальной. В этом случае вводят точку (тело) отсчета. При перемещении точки вектор $overline$ постоянно изменяется. Конец этого вектора описывает траекторию. Движение задает выражение: [overline=overlineleft(tright)left(7right).]
Третьим способом описания движения является описание с помощью параметров траектории.

Путь — это скалярная величина, равная длине траектории.

Если траектория задана, то задачу описания движения сводят к определению закона движения вдоль нее. При этом выбирается начальная точка траектории. Любая другая точка характеризуется расстоянием $s$ по траектории от начальной точки. В таком случае движение описывают выражением:

Пусть по окружности радиуса R равномерно перемещается точка. Закон движения точки по окружности в рассматриваемом методе запишем как:

где $s$ — путь точки по траектории; $t$ — время движения; $A$ — коэффициент пропорциональности. Известными являются окружность и точка начала движения. Отсчет положительных величин $s$ совпадает с направлением перемещения точки по траектории.

Знание траектории движения тела во многих случаях существенно упрощает процесс описания движения тела.

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Примеры задач с решением

Задание: Точка движется в плоскости XOY из начала координат со скоростью $overline=Aoverline+Bxoverline , $где $overline$, $overline$ — орты осей X и Y; $A$,B — постоянные величины. Запишите уравнение траектории движения точки ($y(x)$). Изобразите траекторию. textit

Решение: Рассмотрим уравнение изменения скорости частицы:

Из этого уравнения следует, что:

Для получения уравнения траектории следует решить дифференциальное уравнение (1.3):

Мы получили уравнение параболы, ветви которой направлены вверх. Эта парабола проходит через начало координат. Минимум этой функции находится в точке с координатами:

Задание: Движение материальной точки в плоскости описывает система уравнений: $left< begin x=At. \ y=At(1+Bt) end right.$, где $A$ и $B$ — положительные постоянные. Запишите уравнение траектории точки.

Решение: Рассмотрим систему уравнений, которая задана в условии задачи:

Исключим время из уравнений системы. Для этого из первого уравнения системы выразим время, получим:

Подставим вместо $t$ правую (2.2) часть во второе уравнение системы (2.1), имеем:

Видео:Кинематика точкиСкачать

iSopromat.ru

Пример решения задачи по определению траектории равноускоренного движения точки, заданного уравнениями, скорости и ускорения в некоторые моменты времени, координаты начального положения точки, а также путь, пройденный точкой за время t.

Видео:Способы описания движения. Траектория. Путь. ПеремещениеСкачать

Задача

где x и y – в см, а t – в с. Определить траекторию движения точки, скорость и ускорение в моменты времени t₀=0 с, t₁=1 с и t₂=5 с, а также путь, пройденный точкой за 5 с.

Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Решение

Расчет траектории

Определяем траекторию точки. Умножаем первое заданное уравнение на 3, второе – на (-4), а затем складываем их левые и правые части:

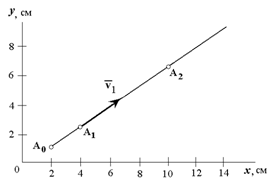
Получилось уравнение первой степени – уравнение прямой линии, значит движение точки – прямолинейное (рисунок 1.5).

Для того, чтобы определить координаты начального положения точки A₀, подставим в заданные уравнения значения t₀=0; из первого уравнения получим x₀=2 см, из второго y₀=1 см. При любом другом значении t координаты x и y движущейся точки только возрастают, поэтому траекторией точки служит полупрямая 3x-4y=2 с началом в точке A₀ (2; 1).

Расчет скорости

Расчет ускорения

Определяем ускорение точки. Его проекции на оси координат:

Проекции ускорения не зависят от времени движения,

т.е. движение точки равноускоренное, векторы скорости и ускорения совпадают с траекторией точки и направлены вдоль нее.

С другой стороны, поскольку движение точки прямолинейное, то модуль ускорения можно определить путем непосредственного дифференцирования уравнения скорости:

Определение пути

Определяем путь, пройденный точкой за первые 5с движения. Выразим путь как функцию времени:

Проинтегрируем последнее выражение:

Если t=t₀=0, то C=s₀; в данном случае s₀=0, поэтому s=2,5t 2 . Находим, что за 5с точка проходит расстояние

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Уравнение прямой по двум точкам

Данный онлайн калькулятор находит формулы параметрического уравнения прямой и уравнения прямой с угловым коэффициентом по координатам двух точек, принадлежащих прямой.

На этой странице вы найдете два калькулятора, которые строят уравнение прямой по координатам двух точек, принадлежащих этой прямой.

Первый калькулятор находит уравнение прямой с угловым коэффициентом, то есть уравнение в форме . Также он строит график и отдельно выводит угловой коэффициент и значение y в месте пересечения прямой с осью ординат.

Второй калькулятор находит параметрические уравнения прямой, то есть систему уравнений вида . Он также строит график и отдельно выводит направляющий вектор.

Формулы расчета можно найти под калькуляторами.