Токовый диполь уравнение дипольного момента (7 видео)

3.2. Электрический диполь

Чтобы понять механизм поведения диэлектриков в поле на микроскопическом уровне, нам надо сначала объяснить, как может электрически нейтральная система реагировать на внешнее электрическое поле. Простейший случай — полное отсутствие зарядов — нас не интересует. Мы знаем наверняка, что в диэлектрике имеются электрические заряды — в составе атомов, молекул, ионов кристаллической решетки и т. д. Поэтому мы рассмотрим следующую по простоте конструкции электронейтральную систему — два равных по величине и противоположных по знаку точечных заряда +q и –q, находящихся на расстоянии l друг от друга. Такая система называется электрическим диполем.

Электрический диполь — это система, состоящая из двух точечных равных по величине и противоположных по знаку зарядов, находящихся на расстоянии l друг от друга (рис. 3.6).

Рис. 3.6. Электрический диполь

Линии напряженности электрического поля и эквипотенциальные поверхности электрического диполя выглядят следующим образом (рис. 3.7, 3.8, 3.9)

Рис. 3.7. Линии напряженности электрического поля электрического диполя

Рис. 3.8. Эквипотенциальные поверхности электрического диполя

Рис. 3.9. Линии напряженности электрического поля и эквипотенциальные поверхности

Основной характеристикой диполя является электрический дипольный момент. Введем вектор l, направленный от отрицательного заряда (–q) к положительному (+q), тогда вектор р, называемый электрическим моментом диполя или просто дипольным моментом, определяется как

Рассмотрим поведение «жесткого» диполя — то есть расстояние которого не меняется — во внешнем поле Е (рис. 3.10).

Рис. 3.10. Силы, действующие на электрический диполь, помещенный во внешнее поле

Пусть направление дипольного момента составляет с вектором Е угол . На положительный заряд диполя действует сила, совпадающая по направлению с Е и равная F₁ = +qE, а на отрицательный — противоположно направленная и равная F₂ = –qE. Вращающий момент этой пары сил равен

Так как ql = р, то М = рЕ sin или в векторных обозначениях

(Напомним, что символ

означает векторное произведение векторов а и b.) Таким образом, при неизменном дипольном моменте молекулы () механический момент, действующий на нее, пропорционален напряженности Е внешнего электрического поля и зависит от угла между векторами р и E.

Под действием момента сил М диполь поворачивается, при этом совершается работа

которая идет на увеличение его потенциальной энергии. Отсюда получаем потенциальную энергию диполя в электрическом поле

если положить const = 0.

Из рисунка видно, что внешнее электрическое поле стремится повернуть диполь таким образом, чтобы вектор его электрического момента р совпал по направлению с вектором Е. В этом случае , а, следовательно, и М = 0. С другой стороны, при потенциальная энергия диполя во внешнем поле принимает минимальное значение , что соответствует положению устойчивого равновесия. При отклонении диполя от этого положения снова возникает механический момент, который возвращает диполь в первоначальное положение. Другое положение равновесия, когда дипольный момент направлен против поля является неустойчивым. Потенциальная энергия в этом случае принимает максимальное значение и при небольших отклонениях от такого положения возникающие силы не возвращают диполь назад, а еще больше отклоняют его.

На рис. 3.11 показан опыт, иллюстрирующий возникновение момента электрических сил, действующих на диэлектрик в электрическом поле. На удлиненный диэлектрический образец, расположенный под некоторым углом к силовым линиям электростатического поля, действует момент сил, стремящийся развернуть этот образец вдоль поля. Диэлектрическая палочка, подвешенная за середину внутри плоского конденсатора, разворачивается перпендикулярно его пластинам после подачи на них высокого напряжения от электростатической машины. Появление вращающего момента обусловлено взаимодействием поляризовавшейся палочки с электрическим полем конденсатора.

Рис. 3.11. Момент электрических сил, действующих на диэлектрик в электрическом поле

В случае неоднородного поля на рассматриваемый диполь будет действовать еще и равнодействующая сила F_paвн, стремящаяся его сдвинуть. Мы рассмотрим здесь частный случай. Направим ось х вдоль поля Е. Пусть диполь под действием поля уже повернулся вдоль силовой линии, так что отрицательный заряд находится в точке с координатой x, а положительный заряд расположен в точке с координатой х + l. Представим себе, что величина напряженности поля зависит от координаты х. Тогда равнодействующая сила F_paвн равна

Такой же результат может быть получен из общего соотношения

где энергия П определена в (3.8). Если Е увеличивается с ростом x, то

и проекция равнодействующей силы положительна. Это значит, что она стремиться втянуть диполь в область, где напряженность поля больше. Этим объясняется известный эффект, когда нейтральные кусочки бумаги притягиваются к наэлектризованной расческе. В плоском конденсаторе с однородным полем они остались бы неподвижными.

Рассмотрим несколько опытов, иллюстрирующих возникновение силы, действующей на диэлектрик, помещенный в неоднородное электрическое поле.

На рис. 3.12 показано втягивание диэлектрика в пространство между обкладками плоского конденсатора. В неоднородном электростатическом поле на диэлектрик действуют силы, втягивающие его в область более сильного поля.

Рис. 3.12. Втягивание жидкого диэлектрика в плоский конденсатор

Это демонстрируется при помощи прозрачного сосуда, в который помещен плоский конденсатор, и налито некоторое количество жидкого диэлектрика — керосина (рис.3.13). Конденсатор присоединен к высоковольтному источнику питания — электростатической машине. При ее работе на нижнем краю конденсатора, в области неоднородного поля, на керосин действует сила, втягивающая его в пространство между пластинами. Поэтому уровень керосина внутри конденсатора устанавливается выше, чем снаружи. После выключения поля уровень керосина между пластинами падает до его уровня в сосуде.

Рис. 3.13. Втягивание керосина в пространство между обкладками плоского конденсатора

В реальных веществах нечасто встречаются диполи, образованные только двумя зарядами. Обычно мы имеем дело с более сложными системами. Но понятие электрического дипольного момента применимо и к системам со многими зарядами. В этом случае дипольный момент определяется как

где , — величина заряда с номером i и радиус-вектор, определяющий его местоположение, соответственно. В случае двух зарядов мы приходим к прежнему выражению

Пусть наша система зарядов электрически нейтральна. В ней есть положительные заряды, величины которых и местоположения мы обозначим индексом «+». Индексом «–» мы снабдим абсолютные величины отрицательных зарядов и их радиус-векторы. Тогда выражение (3.10) может быть записано в виде

В (3.11) в первом слагаемом суммирование ведется по всем положительным зарядам, а во втором — по всем отрицательным зарядам системы.

Электрическая нейтральность системы означает равенство полного положительного заряда и суммы абсолютных величин всех отрицательных зарядов

Введем теперь понятие «центр зарядов» — положительных R + и отрицательных R –

Выражения (3.13) аналогичны формулам для центра масс в механике, и потому мы назвали их центрами положительных и отрицательных зарядов, соответственно. С этими обозначениями и с учетом соотношения (3.12) мы записываем электрический дипольный момент (3.11) системы зарядов в виде

где l-вектор, проведенный из центра отрицательных зарядов в центр положительных зарядов. Смысл нашего упражнения заключается в демонстрации, что любую электрически нейтральную систему зарядов можно представить как некий эквивалентный диполь.

Дополнительная информация

Видео:Диполь. Просто дипольСкачать

Токовый диполь. Эквивалентный электрический генератор.

В электропроводящей среде диполь не сохраняется, т.к. свободные заряды среды, притягиваясь к противоположно заряженным полюсам диполя, либо экранируют его, либо нейтрализуют.

Т.к. электрическое поле, образующееся в организме, не исчезает в процессе жизнедеятельности, то необходима иная модель диполя. Можно представить его как электрический генератор с э.д.с. . Если использовать его в цепи (рис. 9.12), то для этой цепи закон Ома записывается как . Создавая модель диполя как источника электрического поля, мы должны исключить внешнее сопротивление, т.е. исключить влияние среды. Примем , к клеммам источника присоединим диполь (рис.9.13)

Т.е. клеммы источника питания можно рассматривать как полюса диполя, который в проводящей среде будет сохраняться до тех пор, пока функционирует источник тока.

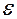
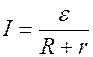
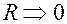
Отрицательный полюс назовем истоком тока, положительный – стоком тока. Такую модель диполя называют токовым диполем.

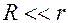
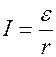
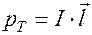
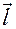
Для токового диполя и . Дипольный момент токового диполя , где — плечо диполя, по модулю этот вектор равен расстоянию между стоком и истоком тока.

Суперпозицию токовых диполей будем называть эквивалентным электрическим генератором.

Контрольные вопросы

•Электрический диполь, его характеристики. Потенциал и разность потенциалов.

•Электрический диполь, его характеристики. Электрическое поле диполя. •Напряженность поля диполя.•Диполь в однородном и неоднородном электрическом поле. •Понятие о дипольном электрическом генераторе (токовый диполь).

Дата добавления: 2015-04-19 ; просмотров: 2786 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Дипольный момент (видео 26) | Химические связи и структура молекул | ХимияСкачать

Лабораторная работа № 4.2

ИЗУЧЕНИЕ ЭЛЕКТРИЧЕСКОГО ПОЛЯ ТОКОВОГО ДИПОЛЯ

Мотивационная характеристика темы. Одной из основных задач электрокардиографии является вычисление распределения трансмембранного потенциала клеток сердечных мышц по потенциалам, измеренным вне сердца. Биофизический подход к выяснению связи между биопотенциалами сердца и их внешним проявлением заключается в моделировании источников этих биопотенциалов. В первом приближении моделировать электрическую активность сердца возможно если использовать дипольный эквивалентный электрический генератор.

Цель лабораторной работы:

Изучить топографию поля электрического диполя, ознакомиться с физическими основами дипольной теории электрической активности сердца Эйтховена.

Знать

Уметь

1.Определение напряженности и потенциала электрического поля. Единицы измерения. 2.Графическое изображение электрического поля. 3.Токовый диполь и его особенности. 4.Каково взаимное расположение силовых линий и эквипотенциальных плоскостей электрического поля.

1.Экспериментально строить эквипотенциальные поверхности электростатического поля. 2.Измерять разность потенциалов между произвольными точками среды, помещенной в электрическое поле.. 2.По разности потенциалов между вершинами треугольника Эйтховена строить положение дипольного момента токового диполя.

1. А.Н.Ремизов. Медицинская и биологическая физика. М.,1999, Гл.14.

2.А.Н.Ремизов. Медицинская и биологическая физика. М.,1987, Гл.14.

3.И.А.Эссаулова и др. Руководство к лабораторным работам по медицинской и биологической физике. М., 1987, Лб.20.

Контрольные вопросы для определения

Исходного уровня знаний

1.Основные характеристики электрического поля. Количественное их определение и единицы измерения.

2.Электрический диполь. Поле электрического диполя. Графическое изображение электрического поля в пространстве.

3.Как меняются параметры электрического поля, если диполь равномерно вращается в пространстве.

4.Порядок выполнения учебных задач лабораторной работы.

Информационный блок

Электрическим диполем (диполем) называют систему, состоящую из двух равных, но противоположных по знаку точечных электрических зарядов, расположенных на некотором расстоянии друг от друга (плечо диполя.

Токовый диполь уравнение дипольного момента

Рис.1

Основной характеристикой диполя является его электрический, или дипольный, момент — вектор, равный произведению заряда на плечо диполя, направленный от отрицательного заряда к положительному.

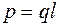
где q – величина одного из двух равных по знаку точечных зарядов, расположенных на расстоянии l друг от друга (рис.1); р — вектор, направленный от отрицательного заряда к положительному.

Единицей измерения дипольного момента является кулон-метр.

Рассмотрим некоторую точку А, удаленную от зарядов диполя на расстоянии r₁. (рис.2). Потенциал в точке А равен:

где e — относительная диэлектрическая проницаемость среды;

e₀ — электрическая постоянная. Предположим, что l 2 , r — r₁ » l cos a, откуда

( 1 )

Пусть диполь находится в точке 0, расстояние между его зарядами мало (рис.3). Запишем, пользуясь формулой, разность потенциалов в двух точках А и В равноотстоящих от диполя:

( 2 )

так как êОС ê ïï çАВç, то

откуда cos a_B — cos a_A =

Cледовательно, ( 3 )

Из полученного выражения видно, что разность потенциалов в двух точках поля диполя (при данном e и r )зависит от синуса половины угла, под которым видны эти точки от диполя, и зависит от проекции электрического момента диполя на прямую, соединяющую точки.

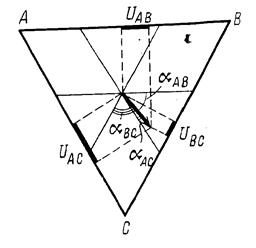Если диполь находится в центре равностороннего треугольника (рис.4), то b_ас = b_вс = b_ав и соотношения между напряжениями на сторонах этого треугольника могут быть получены как соотношения проекций вектора р на стороны треугольника:

где а — угол между диполем и соответствующей стороной треугольника ,

Так как р является постоянной величиной ,то выражение можно переписать в виде

Зная напряжение U_AB , U_AC и U_BC, можно определить, как ориентирован диполь относительно сторон треугольника . Из рис.4 видно, что

Из соотношения ( 5 ) следует, что

где k — коэффициент пропорциональности, зависящий от свойств среды, дипольного момента и размеров треугольника. Используя соотношения ( 20.6) и проделав тригонометрические преобразования, получим

( 7 )

В вакууме или в идеальном диэлектрике электрический диполь может сохраняться сколько угодно долго. В проводящей среде под действием электрического поля диполя возникает движение свободных зарядов и диполь либо экранируется, либо нейтралируется. При подключении к диполю источника постоянного напряжения диполь в слобопроводящей среде будет сохранятся, несмотря на наличие тока. Такая двухполюсная система называется дипольным электрическим генератором или токовым диполем.

Между дипольным электрическим генератором и электрическим диполем имеется аналогия, основанная на общей аналогии электрического поля в проводящей среде с электростатическим полем, которая сводится к следующему:

а) линии тока в проводящей среде совпадают с линиями напряженности электростатического поля при одинаковой форме электродов;

б) зависимости между соответствующими характеристиками полей в обоих случаях описываются аналогичными уравнениями.

Подобно электрическому моменту диполя вводится дипольный момент токового диполя:

где l — расстояние между электродами; I — сила тока.

Потенциал поля токового диполя в безграничной среде выражается формулой, аналогичной ( 1 ):

где g — удельная электрическая проницаемость.

Для токового диполя справедливы выражения (4) и (5). В электрическом отношении сердце можно рассматривать как токовый диполь. За время сердечного цикла изменяется положение диполя в пространстве и дипольный момент. В соответствии с теорией Эйтховена сердце — диполь — расположено в центре равностороннего треугольника, вершины которого условно можно считать находящимися в правой руке, левой руке и левой ноге. В соответствии с формулой (20.4) измерение разности потенциалов между вершинами этого треугольника позволяет определить соотношение между проекциями дипольного момента сердца на стороны треугольника. Теория Эйтховена лежит в основе электрокардиографии.

Описание установки

Установка представляет собой две плоские ванны, заполненные недистиллированной водой (проводящая среда).

Одна ванна открыта, и на дно ее положена измерительная сетка. Напряжение от источника постоянного тока подается на небольшие металлические шарики-электроды, помещенные в ванну. Эта система представляет собой токовый диполь. Шарики укреплены на тонких стержнях и могут перемещаться в двух взаимно перпендикулярных направлениях. Измерения разности потенциалов производится вольтметром, снабженным специальными щупами по схеме рис.5а .

Вторая ванна закрыта непрозрачной крышкой, диполь закреплен в ней неподвижно в центре равностороннего треугольника в положении не известном для экспериментатора. Клеммы для подачи напряжения на диполь и для измерения разности потенциалов между вершинами треугольника расположены на крышке ванны. Измерения проводятся по схеме рис.5б.

Приборы и принадлежности:вольтметр со щупами , диполь , ванна с водой , миллиметровая сетка .

Задание 1. Построить эквипотенциальные линии поля токового диполя.

а) поместите электроды в открытой ванне на расстоянии 4-6 см. друг от друга;

б) подайте напряжение на электроды;

в) подсоедините один электрод к вольтметру;

г) щуп, соединенный со вторым полюсом вольтметра, поместите в точку, расположенную на середине расстояния между электродами, и измерьте разность потенциалов;

д) передвигая щуп, найдите точки, имеющие такой же потенциал, и, определив их координаты по измерительной сетке, нанесите эти точки на миллиметровую бумагу. Соединив полученные точки, получите на рисунке линию равного потенциала (эквипотенциальную линию);

е) постройте еще четыре эквипотенциальные линии других значений потенциала по две с каждой стороны от центральной. Укажите на схеме числовое значение потенциала каждой эквипотенциальной линии;

ж) отметьте на рисунке положение полюсов диполя и проведите линии напряженности от положительного заряда к отрицательному перпендикулярно эквипотенциальным линиям.

Задание 2. Определить разность потенциалов на сторонах равностороннего треугольника.

а) поместите электроды диполя в центре равностороннего треугольника АВС, нарисованного на измерительной сетке, вдоль линии, параллельной одной из его сторон, на расстоянии 4-6 см друг от друга;

б) измерьте разности потенциалов U_AB, U_BC_, U_AC между вершинами треугольника;

в) определите косинусы углов a_АВ, a_ВС, a_АС между диполем и соответствующими сторонами треугольника. Приведите чертеж.

г) результаты измерений занесите в таблицу 1.;

Расположение электродоа

U_AB _B

U_BC _B

U_AC B

cos a_AB

cos a_BC

cos a_AC

д) проверьте, выполняется ли соотношение ( 5 );

е) расположите электроды диполя вдоль одной из высот треугольника АВС и повторите измерения п. Б) — д). Приведите чертеж.

Задание 3. Определить положение токового диполя в непрозрачной среде.

а) подайте напряжение от источника тока на диполь, помещенный в закрытой ванне;

б) измерьте разности потенциалов U_AC и U_BC между вершинами треугольника ;

в) вычислите угол между плечом диполя и стороной АВ треугольника по формуле (7);

г) результаты измерений и вычислений занесите в таблицу 2.

U_AC B

U_BC B

tg a_AB

a_AB_, град

Сделайте вывод в котором объясните вид эквипотенциальных линий в жидкости. Как определить разность потенциалов между произвольными точками среды. Как определить положение токового диполя в среде, пользуясь треугольником Эйтховена.

Вопросы для контроля результатов усвоения

1.Что такое токовый диполь и как рассчитать его дипольный момент?

2.Дать определение напряженности и потенциала электростатического поля.

3.Что определяет закон Кулона?

4.Чему равна разность потенциалов между двумя произвольными точками одной и той же эквипотенциальной поверхности?

5.Как ведет себя свободный диполь в однородном и неоднородном электрическом поле?

6.Основные положения теории Эйтховена.

7.Почему для определения положения диполя в пространстве используют равносторонний треугольник?

8.Как связана разность потенциалов между вершинами равностороннего треугольника с дипольным моментом.