Ток смещения физический смысл уравнений максвелла (8 видео)

Содержание

Ток смещения физический смысл уравнений максвелла
§25. Ток смещения и система уравнений Максвелла
Ток смещения
Физическое содержание тока смещения
Готовые работы на аналогичную тему
Ток смещения в диэлектрике
Полный ток
💥 Видео

Видео:Билеты №32, 33 "Уравнения Максвелла"Скачать

Ток смещения физический смысл уравнений максвелла

Теперь Тесла понимал, почему его переменные заряды высокой частоты из первых опытов никогда не выказывали таких мощных проявлений. Именно прерывистость, яростный импульсный разряд, придавал этому неожиданному «газообразному» компоненту возможность свободно перемещаться. Импульсы, однонаправленные импульсы, были единственной причиной, с помощью которой мог быть высвобожден этот потенциал. Синусоидальные колебания в этом отношении были абсолютно бесполезны.

Секреты свободной энергии холодного электричества. Глава 2. Розеттский камень

Видео:ЧК_МИФ: 4.1.1.ДФ_1 Физический смысл уравнений МаксвеллаСкачать

§25. Ток смещения и система уравнений Максвелла

Мы установили, что изменяющееся магнитное поле порождает изменяющееся электрическое поле, которое в свою очередь порождает изменяющееся магнитное поле и т. д. В результате образуются сцепленные между собой электрическое и магнитное поля, составляющие электромагнитную волну. Она “отрывается” от зарядов и токов, которые ее породили. Способ существования электромагнитной волны делает невозможным ее неподвижность в пространстве и постоянство напряженности во времени.

Постоянный ток не протекает в цепи с конденсатором, а в случае переменного напряжения в цепи ток протекает через конденсатор. Для постоянного тока конденсатор – разрыв в цепи, а для переменного этого разрыва нет. Поэтому необходимо заключить, что между обкладками конденсатора происходит некоторый процесс, который как бы замыкает ток проводимости. Этот процесс между обкладками конденсатора был назван током смещения. Напряженность поля между обкладками конденсатора . Из граничного условия для вектора следует, что диэлектрическое смещение между обкладками , а сила тока в цепи равна . Тогда

, (25.1)

А значит процессом, замыкающим ток проводимости в цепи, является изменение электрического смещения во времени. Плотность тока

. (25.2)

Существование тока смещения было постулировано Максвеллом в 1864 г. и затем экспериментально подтверждено другими учеными.

Почему скорость изменения вектора смещения называется плотностью тока? Само по себе математическое равенство величины , характеризующей процесс между обкладками конденсатора, т. е. равенство двух величин, относящихся к разным областям пространства и имеющим различную физическую природу, не содержит в себе, вообще говоря, какого-то физического закона. Поэтому называть ”током” можно только формально. Для того чтобы придать этому названию физический смысл, необходимо доказать, что обладает наиболее характерными свойствами тока, хотя и не представляет движения электрических зарядов, подобного току проводимости. Главным свойством тока проводимости является его способность порождать магнитное поле. Поэтому решающим является вопрос о том, порождает ли ток смещения магнитное поле так же, как его порождают ток проводимости, или, более точно, порождает ли величина (25.2) такое же магнитное поле, как равная ей объемная плотность тока проводимости? Максвелл дал утвердительный ответ на этот вопрос. Однако наиболее ярким подтверждением порождения магнитного поля током смещения является существование электромагнитных волн. Если бы ток смещения не создавал магнитного поля, то не могли бы существовать электромагнитные волны.

Уравнение Максвелла с током смещения.

Порождение магнитного поля токами проводимости описывается уравнением

(25.3)

Учитывая порождение поля током смещения, необходимо обобщить это уравнение в виде

(25.4)

Тогда, принимая во внимание (25.2), окончательно получаем уравнение

, (25.5)

Являющееся одним из уравнений Максвелла.

Система уравнений Максвелла.

Полученная в результате обобщения экспериментальных данных, эта система имеет вид:

, (25.6)

Эти уравнения называются полевыми и справедливы при описании всех макроскопических электромагнитных явлений. Учет свойств среды достигается уравнениями

, (25.7)

Называемыми обычно Материальными уравнениями среды. Среды линейны, если и нелинейны если . Материальные уравнения, как правило, имеют вид функционалов.

Рассмотрим физический смысл уравнений.

Уравнение I выражает закон, по которому магнитное поле порождается токами проводимости и смещения, являющимися двумя возможными источниками магнитного поля. Уравнение II выражает закон электромагнитной индукции и указывает на изменяющееся магнитное поле как на один из возможных источников, порождающих электрическое поле. Вторым источником электрического поля являются электрические заряды (уравнение IV). Уравнение III говорит о том, что в природе нет магнитных зарядов.

Полнота и совместность системы. Единственность решения.

В случае линейной среды можно исключить из полевых уравнений (25.6) величины в результате чего они становятся уравнениями относительно векторов и , т. е. относительно шести неизвестных (у каждого вектора по 3 проекции). С другой стороны число скалярных уравнений в (25.6) равно восьми. Получается, что система состоит из 8 уравнений для 6 неизвестных. Однако в действительности система не переполнена. Это обусловлено тем, что уравнения I и IV, а также II и III имеют одинаковые дифференциальные следствия и поэтому связаны между собой.

Чтобы в этом убедиться возьмем от уравнения II и производную по времени от уравнения III. Получим:

Т. е. получили одинаковые дифференциальные следствия. Аналогично возьмем от уравнения I:

С из уравнения непрерывности следует, что . Тогда

или . Из IV следует, что

Наличие двух дифференциальных связей и делает систему уравнений Максвелла совместной. Более подробный анализ показывает, что система является полной, а ее решение однозначно при заданных начальных и граничных условиях.

Доказательство единственности решения в общих чертах сводится к следующему. Если имеется два различных решения, то их разность вследствие линейности системы тоже является решением, но при нулевых зарядах и токах и нулевых начальных и граничных условиях. Отсюда, пользуясь выражением для энергии электромагнитного поля и законом сохранения энергии заключаем, что разность решений тождественно равна нулю, т. е. решения одинаковы. Тем самым единственность решения уравнений Максвелла доказана.

Видео:О чем говорят уравнения Максвелла? Видео 1/2Скачать

Ток смещения

Вы будете перенаправлены на Автор24

Видео:3 14 Уравнения МаксвеллаСкачать

Физическое содержание тока смещения

Мы знаем, что постоянный ток в цепи с конденсатором не течет, переменный — протекает. Сила квазистационарного тока во всех элементах цепи, если они соединяются последовательно, одинакова. В конденсаторе, обкладки которого разделяет диэлектрик, ток проводимости, вызванный перемещением электронов, идти не может. Значит, если ток переменный (присутствует переменное электрическое поле), происходит некоторый процесс, который замыкает ток проводимости без переноса заряда между обкладками конденсатора. Этот процесс называют током смещения.

Любое переменное магнитное поле порождает вихревое электрическое поле. Исследуя разные электромагнитные процессы, Максвелл сделал вывод о том, что существует обратное явление: изменение электрического поля вызывает появление вихревого магнитного поля. Это одно из основных утверждений в теории Максвелла.

Так как магнитное поле — обязательный признак любого тока, Максвелл назвал переменное электрическое поле током смещения. Ток смещения следует отличать от тока проводимости, который вызван движением заряженных частиц (электронов и ионов). Токи смещения появляются только в том случае, если электрическое смещение ($overrightarrow$) переменно. Объемная плотность тока смещения определяется как:

Именно вследствие этого физическое содержание предположения Максвелла о токах смещения сводится к утверждению о том, что переменные электрические поля — источники переменных магнитных полей.

Следует заметить, что плотность тока смещения определена производной вектора $overrightarrow$, а не самим вектором.

Готовые работы на аналогичную тему

Видео:Билет №31 "Ток смещения"Скачать

Ток смещения в диэлектрике

По определению вектора электрической индукции ($overrightarrow$):

где $_0$ — электрическая постоянная, $overrightarrow$ — вектор напряженность, $overrightarrow

$ — вектор поляризации. Следовательно, ток смещения можно записать как:

где величина $frac<partial overrightarrow

>$ — плотность тока поляризации. Токи поляризации — токи, которые вызваны движением связанных зарядов, которые принципиально не отличаются от свободных зарядов. Поэтому нет ни чего странного, что токи поляризации порождают магнитное поле. Принципиальная новизна содержится в утверждении, что вторая часть тока смещения ($_0frac<partial overrightarrow>$), не связанная с движением зарядов, также порождает магнитное поле. Получается, что в вакууме, любое изменение электрического поля по времени вызывает магнитное поле.

Однако, надо заметить, что сам термин «ток смещения» для диэлектриков имеет какое-то обоснование, так как в них действительно происходит смещение зарядов в атомах и молекулах. Но этот термин применяется и к вакууму, где зарядов нет, значит, нет их смещения.

Видео:Физика. Лекция 8. Уравнения Максвелла и электромагнитные волны.Скачать

Полный ток

В том случае, если в проводнике течет переменный ток, то внутри него имеется переменное электрическое поле. Значит, в проводнике существует ток проводимости ($j$) и ток смещения. Магнитное поле проводника определено суммой вышеназванных токов, то есть полным током ($overrightarrow$):

В зависимости от электропроводности вещества, частоты переменного тока, слагаемые в выражении (4), играют разную роль. В веществах с хорошей проводимостью (например, металлах) и при низких частотах переменного тока плотность тока смещения невелика, тогда как ток проводимости существенен. В таком случае, током смещения пренебрегают, в сравнении с током проводимости. В веществах с высоким сопротивлением (изоляторах) и при больших частотах тока ведущую роль играет ток смещения.

Оба слагаемых в выражении (4) могут иметь одинаковые знаки и противоположные. Следовательно, полный ток может быть и больше и меньше тока проводимости, может даже быть равен нулю.

Значит, в общем случае переменных токов магнитное поле определяется полным током. Если контур разомкнут, то на концах проводника обрывается только ток проводимости. В диэлектрике между концами проводника присутствует ток смещения, который замыкает ток проводимости. Получается, что если под электрическим током понимать полный ток, то в природе все токи замкнуты.

Задание: Плоский конденсатор заряжен и отключен от источника заряда. Он медленно разряжается объемными токами проводимости, которые появляются между обкладками, так как присутствует небольшая электрическая проводимость. Чему равна напряжённость магнитного поля внутри конденсатора? Считать, что краевых эффектов в конденсаторе нет.

Решение:

Допустим, что поверхностная плотность заряда на обкладках равна $sigma и-sigma .$ В таком случае, модуль вектора электрического смещения ($D$) для плоского конденсатора равен:

Ток смещения можно найти как:

Подставив вместо $D$ правую часть выражения (1.1), имеем:

В соответствии с законом сохранения заряда, можно записать, что:

Полный ток равен:

Для нашего плоского конденсатора, учитывая полученные выражения (1.3), (1.4), имеем:

Ответ: Магнитное поле в конденсаторе равно нулю.

Задание: Допустим, что неограниченную однородную проводящую среду поместили в металлический шар, имеющий заряд $Q$. В этой среде возникнут электрические токи, которые потекут в радиальных направлениях. Покажите, что данная ситуация требует введения тока смещения при описании возникающих полей.

Решение:

Электрические токи, которые текут от (или к ) шару, возбуждают магнитное поле. Определим направление вектора магнитной индукции этого магнитного поля.

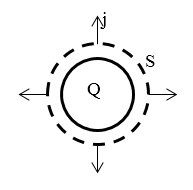
Вектор $overrightarrow$ не имеет радиальной составляющей. Система обдает сферической симметрией. Если бы радиальная составляющая вектора индукции имелась, то она была бы одинаковой для всех точек сферы $S$ (рис.1), концентрической с поверхностью шара, имела направление от центра шара или к его центру. В обоих случаях поток вектора индукции через сферу $S$ был бы не равен нулю, что противоречит уравнению из системы Максвелла:

Значит, вектор индукции магнитного поля должен быть перпендикулярен к радиусу, который проведен из центра шара к рассматриваемой точке. Это также невозможно, так как все направления, перпендикулярные к радиусу, равноправны. Единственная возможность, которая не противоречит симметрии шара, заключается в том, что векторы $overrightarrow и overrightarrow$ всюду равны нулю. Следовательно, равна нулю плотность тока проводимости $overrightarrow, $ что противоречит уравнению:

Для устранения полученного противоречия следует предположить, что магнитные поля порождаются не только токами проводимости. Добавим к току проводимости ток смещения ($I_$), который в нашем случае будет уничтожать возбуждаемое магнитное поле. Его величина определяется из условия:

Ток проводимости, который течет от заряженного шара можно выразить как:

Из выражения (2.3) следует, что:

В соответствии с законом Кулона заряженного проводящего шара, имеем:

[Q=4pi r^2D left(2.6right).]

Найдем производную по времени от заряда, получим:

Плотность тока смещения при этом будет равна:

Полученное выражение совпадает с определением плотности тока смещения.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 02 03 2021