Дата добавления: 2015-06-12 ; просмотров: 5321 ; Нарушение авторских прав
Самое простое уравнение — это линейное уравнение с одной переменной х вида:
Обобщением таких уравнений является линейное уравнение с несколькими переменными х1, х2, . хn вида:
Многие задачи сводятся к решению конечного множества уравнений вида (2), то есть системы линейных уравнений. В общем виде система n линейных уравнений с n переменными x1, x2. xn записывается как совокупность числовых равенств:
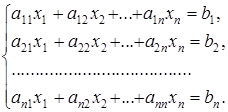
Коэффициенты aij системы для их упорядочения снабжаются двумя индексами, причем индекс i соответствует номеру строки, а j —номеру столбца (i = 1, 2. n; j = 1, 2. n). Тогда свободный член запишется в виде bi(i = 1, 2. n), а переменная— хj (j = 1, 2. n). Будем далее считать, что упорядоченные наборы чисел aij, xj и bi берутся из множества действительных чисел R. Решением системы (3) n уравнений с n переменными называют упорядоченную совокупность n чисел c1, c2, . cn 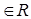
В частном случае, при n = 2 и n = 3 получаем хорошо знакомые системы двух линейных уравнений с двумя переменными:
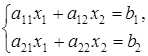
и трех линейных уравнений с тремя переменными:
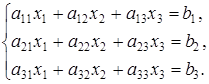
Решением системы (4) является упорядоченная пара чисел (c1, c2), а решением системы (5) — упорядоченная тройка чисел (с1, c2, c3).
Известно, что исследование и нахождение решения для систем (4) и (5) не представляют особых трудностей. Но задачи практического содержания сводятся к исследованию и решению систем линейных уравнений, содержащих десятки, сотни и даже тысячи переменных. Число элементарных операций при решении линейных систем с n переменными пропорционально примерно n 3 , поэтому решение таких задач стало возможным только с появлением быстродействующих ЭВМ.
Не останавливаясь на вопросах исследования систем линейных уравнений, в дальнейшем будем предполагать, что система имеет единственное решение. Поэтому основной задачей этой главы и будет изучение универсальных вычислительных алгоритмов, используемых для нахождения единственного решения системы линейных уравнений, когда число переменных совпадает с числом уравнений.
Методы решения систем линейных уравнений можно разделить на две группы: точные и итерационные (приближенные) методы.
Точными являются такие методы, которые позволяют получить решение системы после выполнения конечного числа арифметических операций над коэффициентами системы и их свободными членами. Причем решение получится точным только тогда, когда коэффициенты и правые части системы (3) известны точно и все арифметические действия над ними выполняются без округлений. Из точных методов рассмотрим метод Гаусса и правило Крамера. Однако на практике даже этими методами не всегда удается получить точное решение, ибо в ЭВМ точные коэффициенты представляются приближенно с некоторой погрешностью, а в процессе вычислений необходимо проводить округление чисел.
Итерационными являются методы, позволяющие получать решение системы с заданной точностью путем сходящихся бесконечных процессов. Из приближенных методов рассмотрим ниже метод итераций.
4.1 Алгоритм метода Гаусса
Пусть дана система n линейных уравнений с n переменными:
Коэффициенты аij при переменных будем рассматривать как элементы двумерного массива A (N, N), а свободные члены bi— как элементы одномерного массива В (N). Решение xi(i = 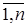
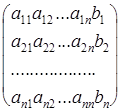
Предписываемые методом Гаусса преобразования будем выполнять над элементами расширенной матрицы. Опишем формально алгоритм решения линейной системы методом Гаусса без выбора главного элемента.
1. Элементы первой строки расширенной матрицы (А | В)делим на а11. Полученную после такого деления первую строку умножаем последовательно на ak1(k = 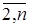
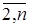
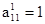

2. Элементы второй строки расширенной матрицы делим на 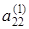
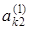
3. Продолжаем этот процесс исключения переменных (получения нулей) до тех пор, пока подобная процедура не будет проделана с (n — 1)-й строкой матрицы. После этого получим матрицу:

4. Элементы n-й строки делим на 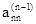

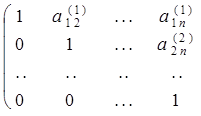
На этом закончился прямой ход метода Гаусса.
5. Выполняем обратный ход метода Гаусса: в (п—1)-ю строку последней матрицы подставляем значение хn и находим значение xn-1, затем последовательно находим xn-2, xn-3, . , x2, x1 по формулам:
Этот алгоритм является экономичным в смысле использования памяти, так как все промежуточные и окончательные значения элементов в процессе преобразования матриц последовательно хранятся в тех же ячейках памяти, что и массивы А и В. Очередные значения диагональных элементов 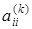
Значения переменных xn, xn-1, . x1 присваиваются элементам массива свободных членов В.
Метод Гаусса с выбором главного элементазаключается в том,что при прямом ходе производится выбор наибольшего по модулю (главного) элемента и перестановка строк или столбцов. Последнее исключает деление на 0, если матрица коэффициентов содержит нулевые элементы, и повышает точность вычислений при наличии ошибок округления. Обычно для программ, ведущих вычисления с числами с плавающей точкой, достаточен выбор Aii ¹ 0.
Метод вращения является разновидностью метода Гаусса. Он обладает повышенной устойчивостью к “провалам” промежуточных вычислений. Этот метод обеспечивает приведение исходной системы к системе с верхней треугольной матрицей (см. литературу).
4.2 Правило Крамера
Правило Крамера рассмотрим на примере двух линейных уравнений с двумя переменными:
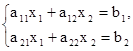
хотя оно применимо и для решения системы n линейных уравнений с n переменными, но с увеличением n требует большого объема вычислительной работы.
Умножим первое уравнение системы (17) на коэффициент а22, а второе — на — a12 и полученные уравнения сложим. Тогда имеем:
Если a11a22 — a21a12 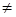
Аналогично, умножая первое уравнение системы (17) на —a21, второе — на а11 и складывая их, получаем:
Введем обозначения: a11a22 — a21a12 = 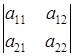
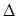
b1a22 — b2a12 =
a11b2 — a21b1 =
Следовательно, 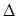
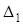
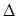
B = 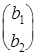
Определитель 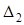
Определитель 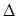
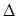
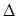
Если главный определитель 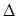
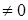
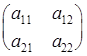
Таким образом, если главный определитель системы уравнений (17) 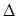
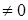
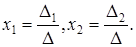
Формулы (18) называются формулами Крамера.
Нахождение решения линейной системы (17) по формулам (18) называется правилом Крамера, который одним из первых пришел к понятию определителя и доказал сформулированное выше предложение.
Справедливы также следующие два предложения:
1. Если главный определитель системы (17) 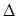
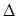
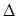
2. Если все три определителя 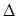
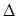
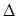
Легко дать геометрическое истолкование этим предложениям. Поскольку каждому уравнению системы (17) в плоскости соответствует некоторая прямая, то система (17) имеет единственное решение, если прямые имеют одну общую точку; не имеет решений, если прямые параллельны; и имеет бесконечное множество решений, если прямые сливаются.
Правило Крамера решения системы n линейных уравнений с n переменными имеет определенное теоретическое значение; практически им уже при n = 4 не пользуются. Установлено, что число операций умножения и деления, которые необходимо выполнить при решении линейной системы алгебраических уравнений порядка n по формулам Крамера, равно:
N(n)= (n 2 — 1)n! + n,
а по схеме единственного деления метода Гаусса:
N(n) = 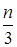
Для сравнения объема вычислительной работы по этим двум алгоритмам подсчитаем количество операций:
по Крамеру по Гауссу
при n = 5 2885 65
при n =10 360*10 6 430
Поэтому все современные ЭВМ имеют стандартные подпрограммы, реализующие различные модификации метода Гаусса.
4.3 Метод итераций и метод Зейделя
Метод итераций позволяет получить последовательность приближенных значений, сходящуюся к точному решению системы линейных уравнений. В отличие от метода Гаусса, метод итераций не требует контроля промежуточных вычислений, так как отдельные ошибки на каком-либо шаге итерации не искажают окончательных результатов, хотя и удлиняет процесс счета. Иначе говоря, метод итераций решения систем линейных уравнений является самоисправляющимся. Кроме того, метод итераций легко запрограммировать для ЭВМ. Пусть имеем систему
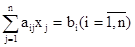
Предположим, что определитель системы отличен от нуля и что диагональные коэффициенты
Выразим из первого уравнения x1, из второго x2, и т. д. Тогда получим эквивалентную систему:
где 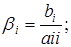
Полученную систему запишем так:
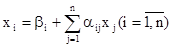
и назовем ее системой нормального вида.
Будем решать ее методом последовательных приближений. За нулевое приближение возьмем, например, столбец свободных членов
Подставив в правую часть системы (20) значения 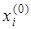
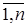
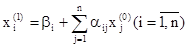
Затем аналогично второе: 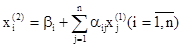
Таким образом, зная k-e приближение, (k + 1)-е приближение вычисляют по формуле 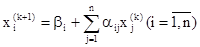
Если последовательность приближений ( 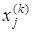
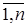
то 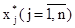
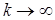
Описанный метод последовательных приближений называется методом итераций. Рабочие формулы метода итераций имеют вид:
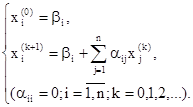
гарантирует теорема о достаточном признаке сходимости процесса итераций.
Достаточным условием сходимости итерационных методов является условие
При методе Зейделя итерационный процесс подобен описанному для метода простых итераций, однако уточненные значения Хi j+1 сразу подставляются в последующие уравнения. Формула итерационного процесса имеет вид:
- Точные и приближенные методы решения систем линейных уравнений. Метод итераций
- Методы решения систем линейных алгебраических уравнений (СЛАУ) с примерами
- Методы решения систем линейных алгебраических уравнений (СЛАУ)
- Метод Крамера
- Матричный способ решения СЛАУ
- Метод Гаусса
- Ранг матрицы. Теорема Кронекера-Капелли
- Следствия из теоремы Кронекера — Капелли
- 🎦 Видео
Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Точные и приближенные методы решения систем линейных уравнений. Метод итераций
Численный метод решения задачи называется точным, если при точном выполнении всех требуемых действий мы получаем точное решение системы. При этом имеется в виду, что все коэффициенты, данные и параметры задачи представляют собой точные значения. Заметим, что методы Гаусса и Жордана — Гаусса, основанные на процессе исключения неизвестных, являются точными.
Если же в результате точного выполнения всех требуемых действий и точном значении всех входящих в условие задачи данных, коэффициентов и параметров получается приближенный результат, то метод называется приближенным. Все рассмотренные в гл. 2 численные методы нахождения корней уравнения являются приближенными.
В случае применения приближенного метода, помимо погрешностей данных, коэффициентов и параметров задачи и погрешностей округления в промежуточных действиях, на окончательный результат всегда влияет и погрешность самого метода.
К числу приближенных методов относится и метод итераций, применимый и к решению систем линейных уравнений. Несмотря на то что данный метод является приближенным, он обладает такими качествами, которые делают его весьма выгодным с вычислительной точки зрения.
Далее кратко рассмотрим метод итераций (к слову, он гораздо проще реализуется в среде Microsoft Excel, чем метод Жордана — Гаусса). Сущность метода изложим на примере системы трех линейных уравнений с тремя неизвестными.
Пусть дана система трех линейных уравнений с тремя неизвестными. Для применения метода итераций приведем систему к виду
Систему вида (3.14) будем называть системой нормального вида. Пусть (х0; j0; z0) есть некоторое грубо приближенное решение системы. Назовем эту совокупность чисел начальным приближением. Если какое-либо грубое приближение неизвестно, то за него можно взять вообще произвольную совокупность значений неизвестных и принять его за начальное приближение. Часто за начальное приближение берут совокупность свободных членов: (Dp, Dp, D3). Подставим числа х0, у0, 2 о в правые части системы (3.14). В левых частях системы (3.14) получаем некоторые значения переменных х, у, z. Обозначим иххьуь zx и назовем первым приближением. Подставив числа х1; уг, zx в правые части системы (3.14), получим второе приближение: х2, y2, z2. Этот процесс можно осуществлять неограниченно. При некоторых условиях, налагаемых на коэффициенты Аь В ь Ci,A2,. С3, к-е приближение хк, ук, zk при возрастании к будет становиться сколь угодно близким к истинному решению системы (х; у*; z»).
Мы говорим в этом случае, что итерационный процесс сходится. Значит, проведя процесс достаточно большое число раз, мы получим приближенное решение системы.
Заметим, что систему (3.14) и аналогичные системы п линейных уравнений с п неизвестными можно записать в матричном виде. Обозначим
Тогда систему (3.14) и аналогичные ей системы п линейных уравнений с п неизвестными можно записать так:
Сформулируем теперь достаточные условия сходимости итерационного процесса.
Достаточные условия сходимости итерационного процесса:
- 1. Сумма модулей элементов каждой строки матрицы А (сумма модулей коэффициентов каждого уравнения системы (3.14)) меньше единицы.
- 2. Сумма квадратов всех элементов каждой строки матрицы А (сумма квадратов коэффициентов каждого уравнения системы (3.14)) меньше единицы.
Найдите решение системы линейных алгебраических уравнений
методом итераций с точностью до 10 -7 .
Найдем сумму модулей коэффициентов при неизвестных в каждом уравнении.
В первом уравнении: 0,12 + 0,18 + 0,08 = 0,38.
Во втором уравнении: 0,15 + 0,06 + 0,11 = 0,32.
В третьем уравнении: 0,04 + 0,10 + 0,09 = 0,23.
Для каждого из уравнений эта сумма меньше единицы, значит, итерационный процесс сходится, и мы можем получить приближенное решение системы методом итераций. Откроем файл «Численные методы линейной алгебры» (Microsoft Excel). Переименуем лист 3 в лист «Метод итераций». Объединим ячейки А1—F1 и поместим туда надпись Начальное приближение. Объединим ячейки Gl—II и поместим туда надпись Матрица системы. В ячейку Л поместим надпись Свободные члены. В ячейки диапазона G2—14 поместим матрицу Л системы, а в ячейки диапазона J2—J4 — свободные члены системы. В ячейку А2 поместим х0=, в ячейку С2 поместим у0=, в ячейку F2 поместим z0=. В ячейки В2, D2 и F2 поместим начальные приближения решения, равные свободным членам системы: -0,64; 0,26; 1,34 соответственно.
Теперь в ячейку АЗ поместим х1=, в ячейку СЗ поместим у1=, в ячейку F3 поместим zl=. В ячейку ВЗ поместим формулу =$G$2*B2+$H$2*D2+$I$2*F2+$J$2 , в ячейку D3 поместим формулу
=$G$3*B2+$H$3*D2+$I$3*F2+$J$31, а в ячейку F3 — формулу
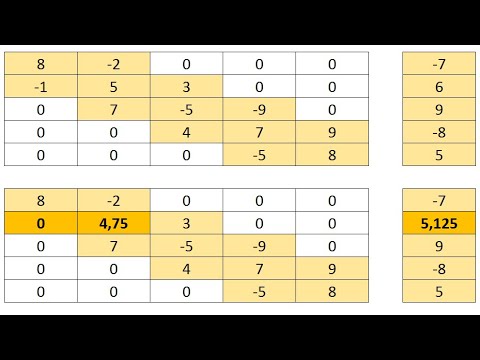
Рис. ЗА. Решение систем линейных уравнений методом итераций
| =$G$4*B2+$H$4*D2+$I$4*F2+$J$4 1. Скопируем ячейки диапазона A3—F3 и последовательно вставляем их вниз до тех пор, пока два соседних значения в каждом из столбцов не станут равными. Эти значения и будут нужными приближениями. Исправляем нумерацию индексов в нужных ячейках столбцов А, С и Е и получаем значения (рис. 3.4):
Округляя полученные значения до семи знаков после запятой, получаем приближенное решение задачи: х
Видео:Базисные решения систем линейных уравнений (03)Скачать

Методы решения систем линейных алгебраических уравнений (СЛАУ) с примерами
Содержание:
Видео:Решение системы уравнений методом ГауссаСкачать

Методы решения систем линейных алгебраических уравнений (СЛАУ)
Метод Крамера
Определение: Системой линейных алгебраических уравнений (СЛАУ) называется выражение
Определение: Определитель, составленный из коэффициентов при неизвестных, называется главным определителем системы
Крамер предложил следующий метод решения СЛАУ: умножим главный определитель на 
Второй столбец умножим на 



Согласно записи СЛАУ первый столбец получившегося определителя представляет собой столбец свободных коэффициентов, т.е.
Определение: Определитель 
Поступая аналогично тому, как описано выше, найдем все вспомогательные определители СЛАУ:
31. Для того чтобы найти вспомогательный определитель i, надо в главном определителе СЛАУ заменить столбец i на столбец свободных коэффициентов.
Определение: Полученные выше соотношения называются формулами Крамера. Используя формулы Крамера, находят неизвестные величины 
- если главный определитель системы отличен от нуля (
), то система имеет единственное решение;
- если главный определитель системы равен нулю (
), а хотя бы один из вспомогательных определителей отличен от нуля (
или
, или, . или
), то система не имеет решений (деление на нуль запрещено);
- если все определители системы равны нулю (
), то система имеет бесчисленное множество решений.
Пример:
Решить СЛАУ методом Крамера
Решение:
Прежде всего, обращаем внимание на то, что в последнем уравнении переменные записаны в неправильном порядке, в этом случае говорят, что СЛАУ записана в ненормализованном виде. Нормализуем СЛАУ, для чего запишем неизвестные в последнем уравнении системы в правильном порядке, чтобы одноименные неизвестные были записаны друг под другом
Найдем главный определитель СЛАУ (раскрываем по первой строке)
Так как главный определитель системы отличен от нуля, то СЛАУ имеет единственное решение. Найдем три вспомогательных определителя
Воспользуемся формулами Крамера
Замечание: После нахождения решения СЛАУ надо обязательно провести проверку, для чего найденные числовые значения неизвестных подставляется в нормализованную систему линейных алгебраических уравнений.
Выполним проверку 
Матричный способ решения СЛАУ
Для решения СЛАУ матричным способом введем в рассмотрение матрицу, составленную из коэффициентов при неизвестных 

Тогда СЛАУ можно записать в матричном виде 





Пример:
Решить СЛАУ матричным способом
Решение:
Введем в рассмотрение следующие матрицы
Найдем матрицу 
Пример:
Решение:
Найдем алгебраические дополнения всех элементов 


Отсюда находим, что х = 1; y = l; z = l.
Метод Гаусса
Метод Гаусса или метод исключения неизвестных состоит в том, чтобы за счет элементарных преобразований привести СЛАУ к треугольному виду. Покажем использование расширенной матрицы, составленной из коэффициентов при неизвестных и расширенной за счет столбца свободных коэффициентов, для приведения СЛАУ к треугольному виду на примере системы, рассматриваемой в этой лекции. Расширенная матрица для СЛАУ имеет вид:
Замечание: В методе Гаусса желательно, чтобы первая строка расширенной матрицы начиналась с единицы.
Обменяем в расширенной матрице первую и вторую строки местами, получим 

Умножим элементы первой строки на (—1) и прибавим к соответствующим элементам третьей строки 

Из первого уравнения находим, что х = 1.
Вывод: Из вышеизложенного материала следует, что вне зависимости от
способа решения СЛАУ всегда должен получаться один и тот же ответ.
Замечание: После нахождения решения СЛАУ надо обязательно выполнить проверку, то есть подставить полученные значения неизвестных в заданную СЛАУ и убедиться в тождественности левой части всех равенств системы соответствующим правым частям. Отметим, что задание СЛАУ всегда верно, то есть, если проверка показывает нарушение оговоренной тождественности, то надо искать ошибку в проведенных вычислениях.
Ранг матрицы. Теорема Кронекера-Капелли
Определение: Рангом матрицы 
Если 
При вычислении ранга необходимо начинать вычислять миноры 2 порядка, затем миноры 3 порядка и так далее, пока не будут найдены миноры, обращающиеся в нуль. Если все миноры порядка p равны нулю, то и все миноры, порядок которых больше p, равны нулю.
Пример:
Найти ранг матрицы
Решение:
Очевидно, что среди миноров второго порядка есть миноры отличные от нуля, например, 


Теорема Кронекера-Капелли (критерий совместности СЛАУ). Для совместности системы линейных алгебраических уравнений (СЛАУ) необходимо и достаточно, чтобы ранг расширенной матрицы совпадал с рангом основной матрицы, составленной из коэффициентов при неизвестных величинах.
Видео:2.2 Итерационные методы решения СЛАУ (Якоби, Зейделя, релаксации)Скачать

Следствия из теоремы Кронекера — Капелли
Следствие: Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение (то есть она определенная).
Следствие: Если ранг матрицы совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений (т.е. она неопределенная).
В случае неопределенной системы решения ищут следующим образом: выбираются главные неизвестные, число которых равно рангу, а остальные неизвестные считаются свободными; далее главные неизвестные выражаются через свободные и получают множество решений, зависящих от свободных неизвестных. Это множество решений называется общим решением системы. Придавая свободным неизвестным различные произвольные значения, получим бесчисленное множество решений, каждое из которых называется частным решением системы.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Скалярное произведение и его свойства
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Матричный метод
- Экстремум функции
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
🎦 Видео
Решение систем линейных уравнений, урок 5/5. Итерационные методыСкачать

Решение систем линейных алгебраических уравнений методом Крамера.Скачать

2.1 Точные методы решения СЛАУ (Крамера, Гаусса, Жордана, прогонки)Скачать
Математика без Ху!ни. Метод Гаусса.Скачать

Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать

Матричный метод решения систем уравненийСкачать

Лекция 5, Итерационные методы решения систем линейных уравненийСкачать

Графическое решение систем уравнений: точные и приближённые ответы | Алгебра IСкачать

Метод простой итерации Пример РешенияСкачать

Метод Зейделя Пример РешенияСкачать

Метод Гаусса решения систем линейных уравненийСкачать

Общее, частное, базисное решение системы линейных уравнений Метод ГауссаСкачать

Решение системы линейных уравнений методом ГауссаСкачать

Метод Ньютона (метод касательных) Пример РешенияСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Быстрое решение системы линейных уравнений в Excel.Скачать

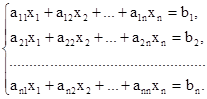
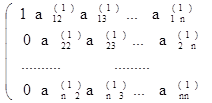
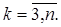
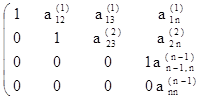
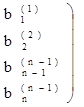
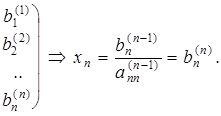
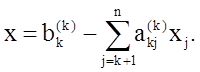
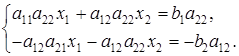
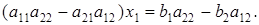
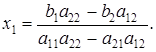
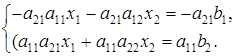
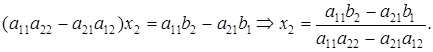
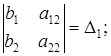
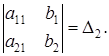
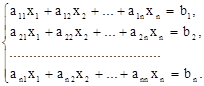
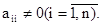
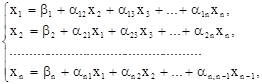

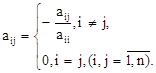
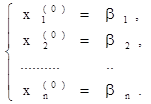
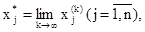
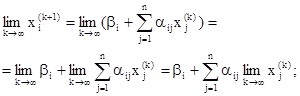
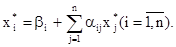
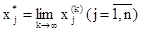
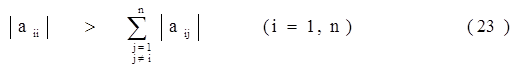












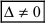 ), то система имеет единственное решение;
), то система имеет единственное решение;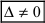 ), а хотя бы один из вспомогательных определителей отличен от нуля (
), а хотя бы один из вспомогательных определителей отличен от нуля ( 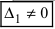 или
или 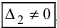 , или, . или
, или, . или 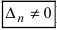 ), то система не имеет решений (деление на нуль запрещено);
), то система не имеет решений (деление на нуль запрещено);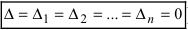 ), то система имеет бесчисленное множество решений.
), то система имеет бесчисленное множество решений.












