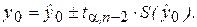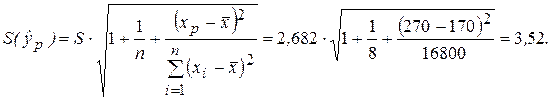Точность прогноза по уравнению регрессии (6 видео)

Прогнозирование с применением уравнения регрессии

Уравнения регрессии применимо и для прогнозирования возможных ожидаемых значений результативного признака. При этом следует учесть, что перенос закономерности связи, измеренной в варьирующей совокупности, в статике на динамику не является, строго говоря, корректным и требует проверки условий допустимости такого переноса (экстраполяции), что выходит за рамки статистики и может быть сделано только специалистом, хорошо знающим объект (систему) и возможности его развития в будущем.

Ограничением прогнозирования на основании регрессионного уравнения, тем более парного, служит условие стабильности или по крайней мере малой изменчивости других факторов и условий изучаемого процесса, не связанных с ними. Если резко изменится “внешняя среда” протекающего процесса, прежнее уравнение регрессии результативного признака на факторный потеряет свое значение. В сильно засушливый год доза удобрений может не оказать влияния на урожайность сельскохозяйственной культуры, так как последнюю лимитирует недостаточная влагообеспеченность.

_{Прогнозируемое значение} _{переменной} _У _{получается при подстановке в уравнение регрессии ожидаемой величины фактора} _Х_:

Следует соблюдать одно ограничение: нельзя подставлять значения факторного признака, значительно отличающиеся от входящих в базисную информацию, по которой вычислено уравнение регрессии. При качественно иных уровнях фактора, если они даже возможны в принципе, были бы другими параметры уравнения. Можно рекомендовать при определении значений факторов не выходить за пределы трети размаха вариации, как за минимальное, так и за максимальное значение признака-фактора, имевшееся в исходной информации.

Прогноз, полученный подстановкой в уравнение регрессии ожидаемого значения фактора, называют точечным прогнозом. Вероятность точной реализации такого прогноза крайне мала. Необходимо сопроводить его расчетом значения средней ошибки прогноза или доверительного интервала прогноза с достаточно большой вероятностью (надежностью).

_{Доверительные интервалы зависят от следующих параметров:}

_{– отклонение} _{от своего среднего значения} _;

_{В частности для прогноза будущие значения} _{с вероятностью}

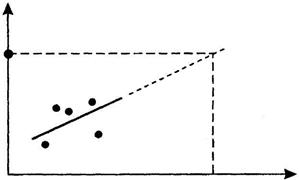
_{Расположение границ доверительного интервала показывает, что прогноз значений зависимой переменной по уравнению регрессии хорош только в случае, если значение фактора Х не выходит за пределы выборки. Иными словами, экстраполяция по уравнению регрессии может привести к значительным погрешностям.}

Видео:Парная регрессия: линейная зависимостьСкачать

Прогнозирование в регрессионных моделях

Одной из центральных задач эконометрики, имеющей большое практическое значение, является прогнозирование значений зависимой переменной при определенных значениях объясняющих (факторных) переменных с использованием построенной регрессионной модели.

В общем случае прогнозирование представляет собой задачу оценки зависимой переменной Y для некоторого набора объясняющих переменных, не входящих в область наблюдаемых статистических данных.

Точечное прогнозирование наиболее наглядно представляется в случае парной линейной регрессии, где возможна графическая экстраполяция (продолжение) линии модели до Х = х_р (рис. 2.3). Если наблюдаемые данные имеют временную структуру (временные ряды), то графическая экстраполяция показывает состояние системы в будущем.

Основным аспектом проблемы прогнозирования является точность прогноза, которая определяется с помощью интервальных оценок зависимой переменной для линейной регрессии.

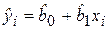
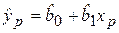
Прогнозирование среднего значения. Пусть построена парная регрессионная модель , на основе которой необходимо предсказать условное математическое ожидание M_x(Y) при Х = х_р. В данном случае значение будет являться выборочной оценкой M_x(Y).

С помощью интервальных оценок, построенных с заданной надежностью (1 – α), для конкретного значения х_р мы можем оценить величину отклонения модельного среднего значения (групповой средней) 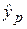от соответствующего математического ожидания.

Для построения доверительного интервала рассчитаем оценку дисперсии .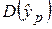

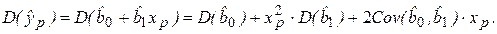
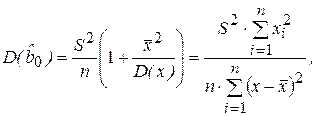
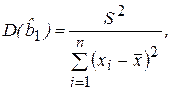
(2.32)

(2.33)

(2.34)

(2.35)

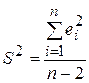
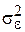
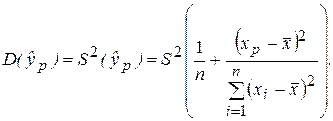
где является несмещенной оценкой теоретической дисперсии случайных отклонений , получим:

(2.36)

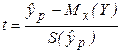
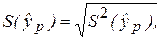
Из положений регрессионного анализа следует, что СВ имеет t-распределение (статистику) Стьюдента с ν = n – 2 степенями свободы. Тогда, зная можно построить доверительный интервал для условного математического ожидания (среднего значения) Y при Х = х_р

(2.37)

соответствующий требуемому уровню значимости α.

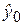
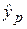
Прогнозирование индивидуальных значений зависимой переменной. Построенная доверительная область для М_х(Y) определяет возможное положение линии модели. Для практических применений более важным моментом является знание допустимых границ (ошибок прогноза) интересующего нас конкретного значения y₀. Предсказанное по уравнению регрессионной модели значение составляет при Х = х_р.

При определении доверительного интервала для индивидуальных значений y₀ зависимой переменной, которые отклоняются от средней, необходимо учитывать еще один источник дисперсии – рассеяние вокруг линии регрессионной модели, которое определяется величиной S 2 . Включив в (2.36) величину S 2 в качестве слагаемого, получим оценку дисперсии индивидуальных значений y₀

(2.38)

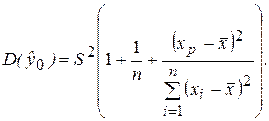
Тогда соответствующий доверительный интервал для прогнозов индивидуальных значений зависимой переменной будет определяться по формуле:

(2.39)

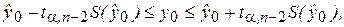
где 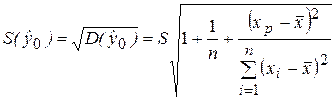представляет собой среднеквадратическую (среднюю стандартную) ошибку прогноза. Тогда предсказанное по уравнению модели значение у₀ можно записать как

Построенный интервал определяет границы значений у₀, за пределами которых могут находиться не более 100 · a наблюдений при Х = х_р. Из формул (2.36) и (2.38) следует, что доверительные интервалы будут наиболее узкими при 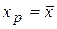и расширяются при удалении х_р от среднего значения (рис. 2.4).

Точность прогноза по уравнению регрессии

С ростом числа наблюдений n доверительные интервалы сужаются (точность прогноза возрастает).

Пример 2.4.С использованием парной регрессионной модели (пример 2.1.) определить прогнозное значение потребления 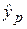при доходе х_р = 270 у.е. и оценить точность прогноза.

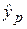
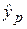
Прогнозное значение потребления определим, подставляя в уравнение регрессии Х = х_р:

= 31,845 + 0,390 · 270 = 137,11 у.е.

Для оценки точности прогноза вычислим среднюю стандартную ошибку по формуле:

Здесь 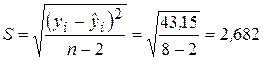– стандартная ошибка регрессионной модели. Расчеты проводим с использованием данных табл. 2.1.

Построим доверительный интервал для y_p, задавая уровень значимости α = 0,05. В соответствии с формулой (2.39) имеем:

137,11 — 2,45 · 3,52 £ y_p £ 137,11 + 2,45 · 3,52.

Таким образом, с вероятностью 0,95 можно утверждать, что уровень потребления при прогнозном значении дохода х_p = 270 у.е. будет находиться в интервале от 128,49 до 145,73 у.е.

Вопросы и упражнения для самопроверки

1. Сформулируйте наиболее общие задачи, решаемые методами регрессионного анализа в экономике.

2. Назовите основные причины присутствия в регрессионной модели случайного отклонения.

3. В чем сущность метода наименьших квадратов (МНК)?

4. Дайте общую интерпретацию коэффициентов (параметров) эмпирического уравнения парной линейной регрессионной модели.

5. Перечислите предпосылки (МНК). Каковы последствия их выполнимости либо невыполнимости?

6. Как определяются стандартные ошибки регрессионной модели и коэффициентов уравнения регрессии?

7. Объясните суть коэффициента детерминации и средней ошибки аппроксимации.

8. Опишите схему проверки статистической значимости коэффициентов регрессии и уравнения модели в целом.

9. Как определяются интервальные оценки коэффициентов регрессии?

10. В чем заключается сущность прогнозирования экономических показателей в регрессионных моделях?

11. Приведите схему определения оценок точности прогноза.

12. По 10 парам наблюдений получены следующие результаты:

; ;

;

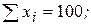
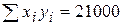
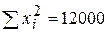
С использованием МНК оцените коэффициенты уравнения регрессии Y на Х.

Оцените выборочный коэффициент корреляции r_xy.

13. При исследовании корреляционной зависимости между ценой на нефть Х и индексом нефтяных компаний Y получены следующие данные:

(ден. ед), (усл. ед), D(x) = 4, Cov(X, Y) = 40.

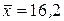
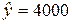
Необходимо: а) составить уравнение регрессии Y на Х; б) используя уравнение регрессии, найти среднее значение индекса при цене на нефть 16,5 ден. ед.

14. В таблице приведены статистические данные об объеме спроса Y и цене Х на некоторый товар:

Х, руб. (цена за ед.товара)

Y, ед.товара

а) постройте корреляционное поле и по расположению точек сделайте предположение о виде зависимости между Х и Y;

б) по МНК постройте регрессионную модель зависимости спроса от цены и проведите общую интерпретацию построенной модели. Изобразите линию модели на корреляционном поле;

в) проверьте общее качество регрессионной модели, рассчитав значения коэффициента детерминации и средней ошибки аппроксимации;

г) рассчитайте характеристики точности оценок коэффициентов регрессии (параметров модели) и оцените статистическую значимость коэффициентов;

д) проведите F-тест, сделайте вывод о статистической значимости уравнения регрессионной модели;

е) оцените прогнозное значение спроса при цене Х_р = 12 руб. и постройте 95%-й доверительный интервал для данного прогноза.

Видео:Точечный прогноз. Интервальный прогноз. Построение уравнения регрессии с помощью анализа данныхСкачать

Эконометрика, её задача и метод. Эконометрические модели и два принципа их спецификации (стр. 4 )

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

Закон распределения пары Px, y(q, r) и формула условной вероятности события p(В/А)=NAB/NA служат основой понятия условного закона распределения случайной переменной.

Функцией регрессии у на х – эта функция обозначается символом Е(у/х) – называется ожидаемое значение случайной переменной у, вычисленное при заданном значении переменной х, т. е.

Величина Е(у/х) является функцией аргумента х. Эта функция позволяет представить случайную переменную у в виде у=Е(у/х)+u, где u – случайная переменная (остаток), такая, что Е(u/x)=0.

Разложение случайной переменной у с таким свойством именуется регрессионным анализом переменной у. Функция регрессии Е(у/х) интерпретируется в эконометрике как выраженный математическим языком экономический закон, по которому изменяется объясняемая (эндогенная) переменная у в ответ на изменения объясняющей (экзогенной) переменной х. В силу свойства дисперсии средний квадрат разброса значений переменной у вокруг величины Е(у/х) оказывается минимальным, при каждом значении переменной х:

Минимум здесь берется по всем возможным функциям f(x). В силу данного свойства функция регрессии Е(у/х) является оптимальным алгоритмом прогнозирования значений переменной у по значениям переменной х:

13. Точность прогноза функцией регрессии.

При использовании уравнения множественной регрессии в целях прогнозирования, необходимо давать точечную и интервальную оценку полученных прогнозных значений зависимой переменной.

Средняя ошибка прогноза ( ) зависит от среднеквадратического отклонения индивидуальных значений от выравненных по уравнению регрессии Se и ошибки положения гиперплоскости регрессии при экстраполяции факторных признаков (расчет этой ошибки производится с применением линейной алгебры, что не входит в программу дисциплины «Эконометрика»).

Доверительный интервал прогноза имеет вид:

При оценке прогноза предпочтительнее проводить интервальное оценивание, поскольку вероятность осуществления точечного прогноза невелика.

Интервал достаточно широк прежде всего за счет малого объема наблюдений. При прогнозировании на основе уравнения регрессии следует помнить, что величина прогноза зависит не только от стандартной ошибки индивидуального значения у^ но и от точности прогноза значения фактора х. Его величина может задаваться на основе анализа других моделей исходя из конкретной ситуации, а также анализа динамики данного фактора.

14. Точность оптимального прогноза для нормально распределённого случайного вектора.

Маргинальные распределения нормально распределенного случайного вектора также являются нормальными.

Таким образом, координаты нормально распределенного случайного вектора не коррелированы тогда и только тогда, когда они независимы.

Таким образом, для нормально распределенного случайного вектора количество информации об одной из составляющих случайного вектора, получаемое в результате наблюдения другой составляющей, зависит только от коэффициента корреляции этих двух составляющих.

Таким образом, координаты нормально распределенного случайного вектора, не коррелированы тогда и только тогда, когда они независимы.

Последовательное оценивание ковариационной матрицы нормально распределенного случайного вектора Xможет быть рассмотрено таким же образом, как оценивание вектора математического ожидания. Предполагается, что вектор математического ожидания известен и, без ограничения общности, — что он равен нулю. Ранее мы предположили, что априорная плотность вероятности р ( Х11) является нормальной. С другой стороны, известно, что выборочная ковариационная матрица имеет распределение Уишарта.

Последовательное оценивание ковариационной матрицы нормально распределенного случайного вектора Xможет быть рассмотрено таким же образом, как оценивание вектора математического ожидания. Предполагается, что вектор математического ожидания известен и, без ограничения общности — что он равен нулю. Ранее мы предположили, что априорная плотность вероятности р ( Х / 1) является нормальной. С другой стороны, известно, что выборочная ковариационная матрица имеет распределение Уишарта. S / 2o, NO), где NO — число объектов и SQ — начальное предположение об истинной ковариационной матрице.

15. Теорема Гаусса-Маркова.

Доказано, что для получения по МНК наилучших результатов (при этом оценки bi обладают свойствами состоятельности, несмещенности и эффективности) необходимо выполнение ряда предпосылок относительно случайного отклонения

Предпосылки использования МНК (условия Гаусса – Маркова)

1. Случайное отклонение имеет нулевое математическое ожидание.

Данное условие означает, что случайное отклонение в среднем не оказывает влияния на зависимую переменную.

2. Дисперсия случайного отклонения постоянна.

Из данного условия следует, что, несмотря на то, что при каждом конкретном наблюдении случайное отклонение ei может быть различным, но не должно быть причин, вызывающих большую ошибку.

3. Наблюдаемые значения случайных отклонений независимы друг от друга.

Если данное условие выполняется, то говорят об отсутствии автокорреляции.

4. Случайное отклонение д. б. независимо от объясняющей переменной.

Это условие выполняется, если объясняющая переменная не является случайной в данной модели.

5. Регрессионная модель является линейной относительно параметров, корректно специфицирована и содержит аддитивный случайный член.

6. Наряду с выполнимостью указанных предпосылок при построении линейных регрессионных моделей обычно делаются еще некоторые предположения, а именно:

случайное отклонение имеет нормальный закон распределения;

число наблюдений существенно больше числа объясняющих переменных;

отсутствуют ошибки спецификации;

отсутствует линейная взаимосвязь между двумя или несколькими объясняющими переменными.

Теорема Гаусса — Маркова

Теорема. Если предпосылки 1 – 5 выполнены, то оценки, полученные по МНК, обладают следующими свойствами:

1. Оценки являются несмещенными, т. е. M[b0] =b0,M[b1] =b1. Это говорит об отсутствии систематической ошибки при определении положения линии регрессии.

2. Оценки состоятельны, т. к. при n®µD[b0]®0,D[b1]®0. Это означает, что с ростом n надежность оценок возрастает.

3. Оценки эффективны, т. е. они имеют наименьшую дисперсию по сравнению с любыми другими оценками данных параметров, линейными относительно величин yi.

16. Понятие статистической процедуры оценивания параметров эконометрической модели. Линейные статистические процедуры. Требования к наилучшей статистической процедуре: несмещённость и минимальные дисперсии оценок параметров

Оценкой ânпараметра a называют всякую функцию результатов наблюдений над случайной величинойX(иначе — статистику), с помощью которой судят о значениях параметра a.

Статистические проверки параметров регрессии основаны на непроверяемых предпосылках распределения случайной величины. Они носят лишь предварительный характер. После построения уравнения регрессии проводится проверка наличия у оценок тех свойств, которые предполагались. Связано это с тем, что оценки параметров регрессии должны отвечать определенным критериям: быть несмещенными, состоятельными и эффективными. Эти свойства оценок, полученных по МНК, имеют чрезвычайно важное практическое значение в использовании результатов регрессии и корреляции.

В отличие от параметра, его оценка ã n— величина случайная. «Наилучшая оценка» ãnдолжна обладать наименьшим рассеянием относительно оцениваемого параметраa, например, наименьшей величиной математического ожидания квадрата отклонения оценки от оцениваемого параметра М(ã — a)2.

Оценка â n параметра a называется несмещенной, если ее математическое ожидание равно оцениваемому параметру, т. е. М(ã) =a.

В противном случае оценка называется смещенной.