Про уравнения - легко » Статьи

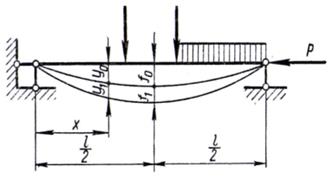
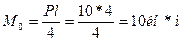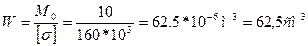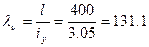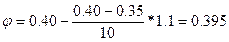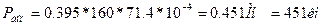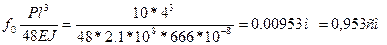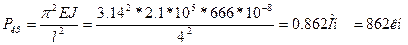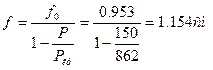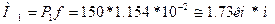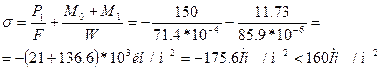Точное решение дифференциального уравнения продольно поперечного изгиба

Обновлено
Содержание
  1. Продольно-поперечный изгиб
  2. Продольно-поперечный изгиб при одновременном приложении к стержню
  3. Продольно-поперечный изгиб
  4. ПроСопромат.ру
  5. Технический портал, посвященный Сопромату и истории его создания
  6. Продольно–поперечный изгиб стержней
  7. 💥 Видео

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

18+ Математика без Ху!ни. Дифференциальные уравнения.

Продольно-поперечный изгиб

Рассмотрим шарнирно опертую по концам балку (рис.1), которая находится под действием поперечной нагрузки и централь­но приложенной силы Р.

Точное решение дифференциального уравнения продольно поперечного изгиба

Допустим, что сначала действовала только поперечная нагрузка, которая вызвала изгиб балки. Обозначим через у0 и М0 прогиб и изгибающий мо­мент в любом сечении бал­ки и примем это состоя­ние за начальное.

Приложим теперь к стержню, имеющему предварительное начальное искривление, сжимающую силу Р, тогда балка изогнется еще больше и прогиб б каждом сечении увеличится на величину y1. Полный прогиб ее в любом сечении

Величина полного прогиба будет плечом для сжимающей силы Р, следовательно, в каждом сечении балки помимо момента М0 от действия поперечной нагрузки появится момент Мг от силы Р:

Обозначим кривизну балки от действия поперечной нагрузки через 1/r0. Так как сжимающая сила увеличивает изгиб балки, то общая кривизна балки от действия поперечной нагрузки и сжимаю­щей силы Р будет 1/r. Значит, приращение кривизны, вызываемое сжимающей силой Р, составит

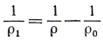
Точное решение дифференциального уравнения продольно поперечного изгиба. (2)

Так как приращение кривизны вызвано изгибающим момен­том М1, то кривизна 1/r1 и изгибающий момент М1 оказываются связанными соотношением

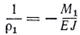
Точное решение дифференциального уравнения продольно поперечного изгиба. (3)

Выразим приращение кривизны через вторую производную от приращения прогиба у1:

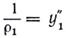
Точное решение дифференциального уравнения продольно поперечного изгиба.

Подставив кривизну 1/r0 и изгибающий момент М1 в формулу (3), получим

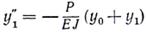
Точное решение дифференциального уравнения продольно поперечного изгиба.

Перенесем неизвестные в этом уравнении в левую часть и, обозначив k 2 =P/EJ, запишем дифференциальное уравнение продольно-поперечного изгиба:

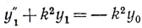
Точное решение дифференциального уравнения продольно поперечного изгиба. (4)

Это уравнение полностью совпадает с уравнением, запи­санным для стержня, имеющего небольшое начальное искривление. Правая часть его у0=у0 (х) представляет собой изогнутую ось балки от действия поперечной нагрузки.

Таким образом, составлению дифференциального уравнения продольно-поперечного изгиба должен предшествовать расчет, в результате которого находится изогнутая ось балки от действия поперечной нагрузки.

Предположим, что изогнутая ось балки найдена. Тогда, под­ставляя выражение у0=у0 (х) в правую часть уравнения (4) и производя интегрирование, найдем приращение прогибов у1 и изгибающих моментов М1 в любом сечении балки от действия сжимающей силы. Складывая изгибающий момент М1 от силы Р сизгибающим моментом М0 от поперечной нагрузки, найдем пол­ный изгибающий момент в любом сечении стержня.

Решение задачи можно значительно упростить, если предста­вить изогнутую ось балки от поперечной нагрузки в силу ее поло­гости в виде полуволны синусоиды со стрелой, равной максималь­ному прогибу балки:

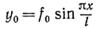
Точное решение дифференциального уравнения продольно поперечного изгиба.

Предположим также, что дополнительные прогибы у в каждом сечении балки от действия сжимающей силы Р распределяются по закону синуса:

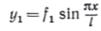
Точное решение дифференциального уравнения продольно поперечного изгиба.

Подставляя принятые приближенные решения в уравнение (4), получим

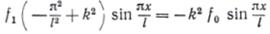
Точное решение дифференциального уравнения продольно поперечного изгиба.

Отсюда найдем стрелу прогиба f1:

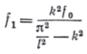
Точное решение дифференциального уравнения продольно поперечного изгиба.

Это решение полностью совпадает с решением задачи о стержне, имеющем небольшое начальное искривление. Поэтому запишем сразу оконча­тельную формулу для вычисления полного прогиба в середине стержня:

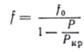
Точное решение дифференциального уравнения продольно поперечного изгиба. (5)

Изгибающий момент в любом сечении стержня от действия сжи­мающей силы Р определим по формуле

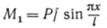
Точное решение дифференциального уравнения продольно поперечного изгиба.

Проверка стержня на прочность производится по наибольшему изгибающему моменту. Для этого сначала найдем наибольший изгибающий момент М0 от действия поперечной нагрузки и опре­делим сечение, в котором действует этот момент. Пусть это сечение будет х=с. Затем определим изгибающий момент М1 в этом сечении от действия сжимающей силы Р:

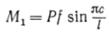
Точное решение дифференциального уравнения продольно поперечного изгиба.

Складывая эти моменты, найдем полный изгибающий момент в этом сечении

При проверке на прочность нужно потребовать, чтобы напря­жения в крайних волокнах наиболее опасного сечения не превы­шали допускаемых:

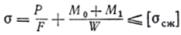
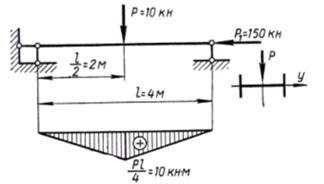
Точное решение дифференциального уравнения продольно поперечного изгиба.

Пример 1:Балка длиной l=4 м загружена в середине пролета вертикальной силой Р=10 кн и сжимается центрально приложен­ной силой P1=150 кн (рис. 2). Подобрать сечение в виде дву­тавра, материал — Ст. 3.

Решение: Сначала подберем сечение из условия попереч­ного изгиба. Максимальный изгибающий момент в середине про­лета

Точное решение дифференциального уравнения продольно поперечного изгиба

Определим требуемый момент сопротивления:

Точное решение дифференциального уравнения продольно поперечного изгиба

По сортаменту нужно принять двутавр № 36. Однако, учитывая неблагоприятное влияние сжимающей силы, примем сечение с не­которым запасом: двутавр № 40, .F=71,4 см 2 , Jу=666 см 4 , Wу==85,9 см 3 , iy=3.05 см.

Точное решение дифференциального уравнения продольно поперечного изгиба

Проверим подобранное сечение на устойчивость в плоскости наименьшей жесткости. Гибкость стержня

Точное решение дифференциального уравнения продольно поперечного изгиба

Выпишем значения коэффициентов j:

Вычислим значение j для Х= 131,1:

Точное решение дифференциального уравнения продольно поперечного изгиба

Допускаемая сжимающая сила

Точное решение дифференциального уравнения продольно поперечного изгиба

Так как сжимающая сила принята Р1=150 кн, то устойчивость стержня обеспечена.

Проверим теперь фактические напряжения в крайних волокнах наиболее опасного сечения. Максимальный прогиб в середине стержня от поперечной нагрузки

Точное решение дифференциального уравнения продольно поперечного изгиба

Для того чтобы вычислить полный прогиб, найдем сначала величину критической силы

Точное решение дифференциального уравнения продольно поперечного изгиба

Полный прогиб в середине стержня

Точное решение дифференциального уравнения продольно поперечного изгиба

Вычислим дополнительный изгибающий момент от действия сжимающей силы:

Точное решение дифференциального уравнения продольно поперечного изгиба

Полный наибольший изгибающий момент и в середине стержня

Определим наибольшие сжимающие напряжения:

Точное решение дифференциального уравнения продольно поперечного изгиба

Подобранное сечение удовлетворяет условию прочности.

Видео:Частное решение дифференциального уравнения. 11 класс.Скачать

Частное решение дифференциального уравнения. 11 класс.

Продольно-поперечный изгиб при одновременном приложении к стержню

Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба

Точное решение дифференциального уравнения продольно поперечного изгиба

Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравнения

Продольно-поперечный изгиб

  • Продольный и поперечный изгиб При одновременном приложении к стержню сжимающей силы и поперечной нагрузки происходит так называемый продольно-поперечный изгиб. Вы можете использовать принцип независимости от силы при одновременном сжатии и

изгибе крупных элементов, таких как опоры моста. Другими словами, вы можете найти напряжение и деформацию отдельно от сжатия и изгиба, а затем суммировать результаты. Этот метод не может

быть распространен на гибкие стержни. Гибкий стержень И получается Людмила Фирмаль

алгебраически- Испытания на сжатие с изгибом должны проводиться по так называемой схеме деформирования. (Пример этого уже обсуждался в пункте 131.) Из-за деформации стержня происходит смещение, поэтому продольные сжимающие силы создают дополнительные изгибающие моменты. Изгибающий момент от

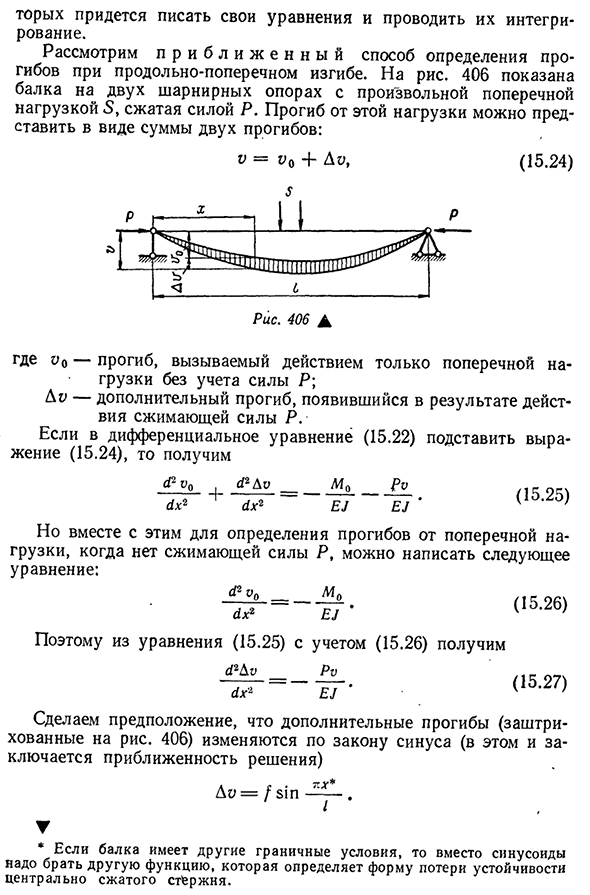
продольной силы важен, и поэтому его нельзя игнорировать. Случай будет описан ниже. 404, изгибающий момент может быть определен как сумма двух моментов: L4-L4o и-R o, (15.21) где 44 0-единственный момент от боковой силы из уравнения (15.21), общий изгибающий

  • момент секции стержня может быть вычислен только при наличии смещения V. следовательно, задача продольно-поперечного изгиба является статически неопределенной задачей. Для «точного» * решения задачи продольного и поперечного изгиба необходимо составить и решить дифференциальные уравнения для оси криволинейной балки: Mo Ru yx2_______е] Поскольку в этом реш

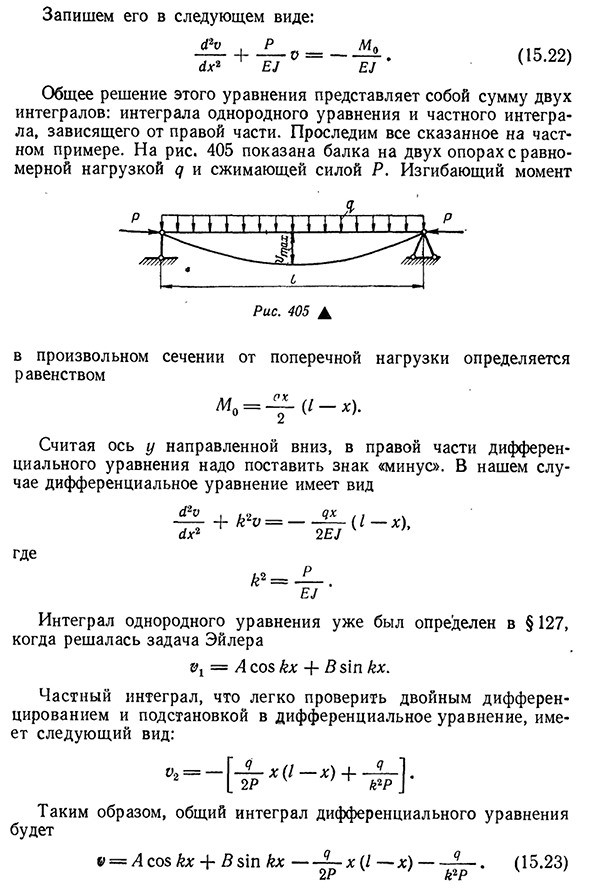
ении используется приближенное дифференциальное уравнение, термин «строгий» применяется здесь условно. Шестнадцать. 483(15.22)) Давайте напишем его в следующем формате: С.= AH2E^e^общим решением этого уравнения является сумма двух интегралов, которые зависят от интегралов однородного уравнения и интегралов правой части. Давайте проследим все это на конкретных примерах. Для риса. 405 показана балка на двух опорах с равномерной нагрузкой d и сжимающей силой P

изгибающим моментом На любом поперечном сечении поперечная нагрузка Людмила Фирмаль

определяется Р авством Л40= — у-(/- Х). Если рассматривать ось y, которая направлена вниз, то справа от дифференциального уравнения нужно поставить знак минус. В этом случае дифференциальное уравнение принимает вид а^

а+= — ГЛ.. 2е? Куда? Интеграл однородного уравнения был уже определен в§127, когда была решена задача Эйлера=a coz KX4-in81p KX. Частные интегралы, которые легко проверяются двойными производными и заменами в дифференциальных уравнениях, принимают вид: Таким образом, общий Интеграл дифференциального уравнения выглядит следующим образом &=Поп-ч+W81P ч — — — — — — — — — ч(1-ч) — — — — — — — д -. 2Р k2p(15.23)) 484 естественные константы L и B получены из граничных условий.Х=О в=0;х==я о = 0. Уравнение, зависящее от этих условий(15.23), получим

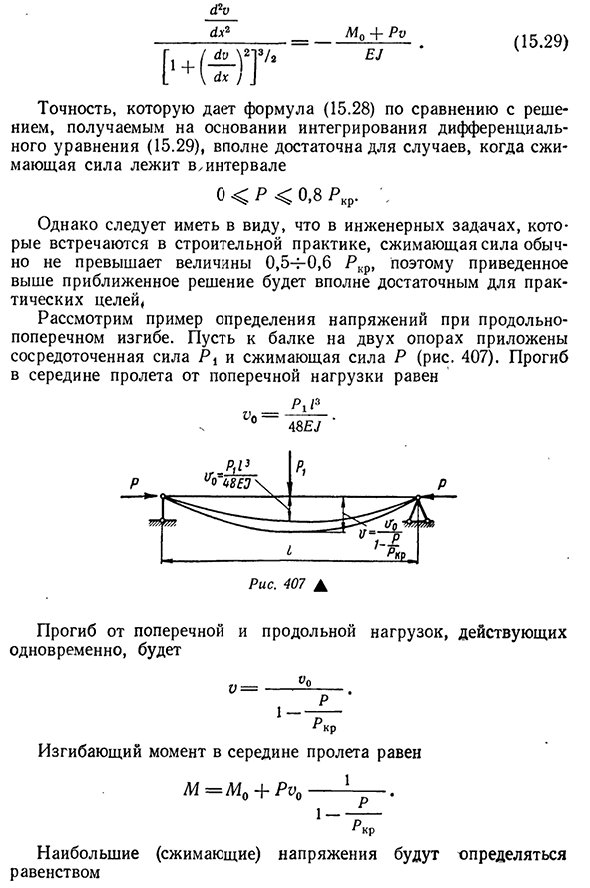
два уравнения: Л- — — — =0;Л-поп м+Vz1p К1———— = 0. Если мы решим эти уравнения относительно констант L и B и присвоим им Интеграл(15.23)、 о= — РК 1-поп-К1 81P м 81P&л- — — — — д-ч(1-ч)- — — — — — 2Р С * Р Соз Х+ Преобразовать значение К1: — //М2 В ем* ] / «РКР» 2/2 К= Тогда есть отклонение. К2″. G. x — 2. ■— — — ———Г8 1П———= ——- /ХV. (1×2/2I P если вы присваиваете результирующее выражение выражению (15.27 г / 2е]’ Или в соответствии с равенством (15.24) -2. X Px) I21 Здесь. О • Для рассматриваемого случая, учитывая, что значение является уравнением критической силы Эйлера, мы, наконец, получаем (15.28)) Эта формула может быть использована и в других случаях фиксации конца стержня, причем РКР должен определяться каждый раз с учетом характера фиксации стержня по общей формуле. п TG2E / …… . Р (^/) 2′ Где 3-момент инерции, соответствующий изгибу данной плоскости. Когда значение отклонения определено, легко определить

изгибающий момент и после этого определить усилие соответствуя раздела. Следует отметить, что приближенная формула (15.28)не может быть использована, если сила сжатия Р близка к критической силе. Следует отметить, что приведенное выше «точное» решение не дает желаемого результата даже в этом случае. В этих случаях необходимо исходить из дифференциальных уравнений 487sru(1х2 ±М0 Р У Е^ (15.29)) Точность, задаваемая формулой (15.28) по сравнению с решением, полученным на основе Интеграла дифференциального уравнения(15.28), достаточна, если сжимающая сила находится в интервале OPP — — — — — — — — — B -. ^ * ВОЗВРАТ КАРЕТКИ

Максимальное (сжимающее) напряжение определяется уравнением Четыреста восемьдесят восемь I1 Р УГ я / Р г КР Невозможно судить о величине напряжения на запасе прочности при заданной нагрузке, поскольку напряжение нелинейно связано с силой R, как при расчете внецентрового сжимающего гибкого стояка при продольном и поперечном изгибе стержня. Для уточнения этой задачи можно построить график изменения напряжений, которые зависят от силы Р, а также график, показанный на рисунке. 402. Однако для больших сил сжатия необходимо также проверить формулу (15.20).

Точное решение дифференциального уравнения продольно поперечного изгиба

Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба Точное решение дифференциального уравнения продольно поперечного изгиба

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Видео:Особые решения дифференциальных уравнений, огибающая семейства кривых | Лекция 34 | МатанализСкачать

Особые решения дифференциальных уравнений, огибающая семейства кривых | Лекция 34 | Матанализ

ПроСопромат.ру

Видео:Понимание напряжений в балкахСкачать

Понимание напряжений в балках

Технический портал, посвященный Сопромату и истории его создания

Видео:Дифференциальные уравнения. 11 класс.Скачать

Дифференциальные уравнения. 11 класс.

Продольно–поперечный изгиб стержней

На практике довольно часто встречаются случаи, когда сравнительно гибкие стержни подвергаются одновременному действию продольных и поперечных нагрузок.

Точное решение дифференциального уравнения продольно поперечного изгиба

При решении задач сложного сопротивления используется принцип независимости действия сил. В таком случае формула для напряжений будет выглядеть так:

Точное решение дифференциального уравнения продольно поперечного изгиба (1)

При продольно-поперечном изгибе yо – прогиб, получившийся от поперечной нагрузки P , может значительно вырасти благодаря действию нагрузки N . При больших прогибах y1 формула (1) станет уже непригодной и при определении величины Точное решение дифференциального уравнения продольно поперечного изгиба необходимо будет учесть еще и напряжения, возникающие от момента N y1, и тогда:

Точное решение дифференциального уравнения продольно поперечного изгиба (2)

Для определения наибольшего нормального напряжения нужно уметь находить прогиб от совместного действия продольных и поперечных сил. Решим эту задачу, интегрируя дифференциальное уравнение упругой линии стержня.

В сечении m-n Точное решение дифференциального уравнения продольно поперечного изгиба

Координата y здесь отрицательная:

Точное решение дифференциального уравнения продольно поперечного изгиба

Общий интеграл этого линейного неоднородного уравнения второго порядка:

Точное решение дифференциального уравнения продольно поперечного изгиба

Граничные условия:

Точное решение дифференциального уравнения продольно поперечного изгиба

из 1) следует, что Точное решение дифференциального уравнения продольно поперечного изгиба, второе условие принимает вид:

Точное решение дифференциального уравнения продольно поперечного изгиба

Точное решение дифференциального уравнения продольно поперечного изгиба

Наибольшей прогиб при Точное решение дифференциального уравнения продольно поперечного изгиба

Точное решение дифференциального уравнения продольно поперечного изгиба (3)

Если продольная сила N стремится к нулю, то

Точное решение дифференциального уравнения продольно поперечного изгиба

С увеличением силы N прогиб стержня растет, при Точное решение дифференциального уравнения продольно поперечного изгиба прогиб становится бесконечно большим, так как

Точное решение дифференциального уравнения продольно поперечного изгиба

Подставим (3) в (2):

Точное решение дифференциального уравнения продольно поперечного изгиба (4)

где Точное решение дифференциального уравнения продольно поперечного изгиба – наибольшее значение момента от поперечной нагрузки. Из формул (4) видно, что нормальные напряжения в стержне не пропорциональны внешним силам, а растут быстрее их.

Действительно, при увеличении продольной силы и поперечной нагрузки в К раз увеличивается и величинаТочное решение дифференциального уравнения продольно поперечного изгиба , благодаря этому растет и отношение Точное решение дифференциального уравнения продольно поперечного изгиба , то есть величина напряжения Точное решение дифференциального уравнения продольно поперечного изгибаТочное решение дифференциального уравнения продольно поперечного изгиба

увеличивается более чем в К раз.

Это обстоятельство необходимо иметь в виду при составлении уравнения для проверки прочности стержня, подвергающегося совместному действию продольных и поперечных сил.

Точное решение дифференциального уравнения продольно поперечного изгиба

Безопасное состояние: Точное решение дифференциального уравнения продольно поперечного изгиба (5)

где геометрические характеристики берутся относительно нейтральной оси сечения, перпендикулярной плоскости действия поперечной нагрузки.

Помимо проверки прочности по уравнению (5) в тех случаях, когда поперечная нагрузка действует в плоскости наибольшей жёсткости, должна быть произведена еще и проверка устойчивости стержня в плоскости наименьшей жесткости.

Точное решение дифференциального уравнения продольно поперечного изгиба

В случае (а) должна быть произведена проверка прочности стержня на совместное действие продольных и поперечных сил по уравнению (5), причем осевой момент сопротивления сечений и осевой момент инерции должны быть определены относительно оси у.

В случае (б) кроме проверки по уравнению (5), куда войдут осевой момент сопротивления и момент инерции, вычисленные относительно оси z, должна быть выполнена проверка по формуле Эйлера, в которую войдет значение осевого момента инерции , вычисленное относительно оси у.

💥 Видео

Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать

Решение дифференциальных уравнений. Практическая часть. 11 класс.

Общее и частное решение дифференциального уравненияСкачать

Общее и частное решение дифференциального уравнения

Откуда появляются дифференциальные уравнения и как их решатьСкачать

Откуда появляются дифференциальные уравнения и как их решать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами

1202.Дифференциальные уравненияСкачать

1202.Дифференциальные уравнения

РК5. Сопротивление материалов (спецкурс). Продольно-поперечный изгиб стержняСкачать

РК5. Сопротивление материалов (спецкурс). Продольно-поперечный изгиб стержня

Сопромат. Устойчивость. Продольный изгиб. Подбор сечения.Скачать

Сопромат. Устойчивость. Продольный изгиб. Подбор сечения.

16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами

Решение физических задач с помощью дифференциальных уравненийСкачать

Решение физических задач с помощью дифференциальных уравнений

Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать

Решение дифференциальных уравнений. Практическая часть. 11 класс.

Сопротивление материалов. Лекция: прямой изгиб балокСкачать

Сопротивление материалов. Лекция: прямой изгиб балок

Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать

Решение дифференциальных уравнений. Практическая часть. 11 класс.
Поделиться или сохранить к себе: