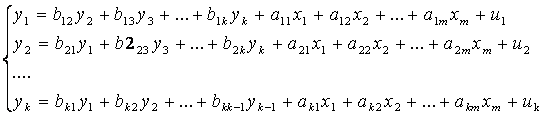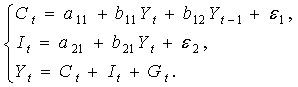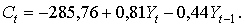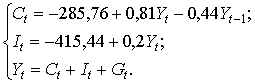Пример . Рассмотрим модель зависимости общей величины расходов на питание от располагаемого личного дохода (х) и цены продуктов питания (р):у = а0 + а1х + а2р + ε. Определим класс модели и вид переменных модели: регрессионная модель с одним уравнением; эндогенная переменная — расходы на питание, экзогенные переменные — располагаемый личный доход и цена продуктов питания.
Принципиальные сложности применения систем эконометрических уравнений связаны с ошибками спецификации модели.
Система уравнений в эконометрических исследованиях может быть построена по-разному. Выделяют следующие 3 вида систем уравнений.
- Система независимых уравнений, когда каждая зависимая переменная (y ) рассматривается как функция только от предопределенных переменных (х):
- Система рекурсивных уравнений, когда в каждом последующем уравнении системы зависимая переменная представляет функцию от зависимых и предопределенных переменных предшествующих уравнений:
От структурной формы легко перейти к так называемой приведенной форме модели. Число уравнений в приведенной форме равно числу эндогенных переменных модели. В каждом уравнении приведенной формы эндогенная переменная выражается через все предопределенные переменные модели:
Так как правая часть каждого из уравнений приведенной формы содержит только предопределенные переменные и остатки, а левая часть только одну из эндогенных переменных, то такая система является системой независимых уравнений. Поэтому параметры каждого из уравнений системы в приведенной форме можно определить независимо обычным МНК.
Зная оценки этих приведенных коэффициентов можно определить параметры структурной формы модели. Но не всегда, а только если модель является идентифицируемой.
Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать
Проблема идентификации
Количество структурных и приведенных коэффициентов одинаково в модели идентифицируемой.
Видео:9 класс, 14 урок, Системы уравнений как математические модели реальных ситуацийСкачать
Правила идентификации
Ранг данной матрицы равен 1, что меньше К-1=2, следовательно, 1-ое уравнение модели неидентифицированно.
Составим матрицу А для 2-ого уравнения системы. Во 2-ом уравнении отсутствуют переменные y3, x2, х3:
y3 x 2 x3
b13 a 13 0 — в 1-ом уравнении
1 a32 a33 — в 3-ем уравнении
Ранг данной матрицы равен 2, что равно К-1=2, следовательно, 2-ое уравнение модели точно идентифицированно.
Составим матрицу А для 3-его уравнения системы. В 3-ем уравнении отсутствуют переменные y1, x2:
y 1 x 2
1 a12 — в 1-ом уравнении
b21 0 — во 2-ом уравнении
Ранг данной матрицы равен 1, что меньше К-1=2, следовательно, 3-е уравнение модели неидентифицированно.
Сделаем выводы: 1-ое и 3-е уравнения системы неидентифицированны (т.к. не выполняются достаточные условия идентификации, а в случае 1-ого уравнения и необходимое условие также). 2-ое уравнение системы сверхидентифицированно. Следовательно, система в целом является неидентифицируемой.
Для оценки параметров 2-ого уравнения можно применить двухшаговый МНК. Параметры 1-ого и 3-его уравнений определить по коэффициентам приведенной формы нельзя. Поэтому модель должна быть модифицирована.
Видео:Рациональные уравнения как математические модели реальных ситуаций (урок 1)Скачать
Эконометрика, её задача и метод. Эконометрические модели и два принципа их спецификации (стр. 23 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
Если все уравнения системы сверхидентифицируемые, то для оценки структурных коэффициентов каждого уравнения используется ДМНК. Если в системе есть точно идентифицируемые уравнения, то структурные коэффициенты по ним находятся из системы приведенных уравнений.
Трехшаговый метод наименьших квадратов применяется тогда, когда нарушено условие гомоскедастичности или когда случайные составляющие коррелированы. Алгоритм трехшагового метода наименьших квадратов (ТМНК) в качестве первых двух шагов включает этапы двухшагового метода,
т. е. для оценки коэффициентов каждого уравнения структурной формы по-прежнему применяется двухшаговый МНК. Оценки, полученные после ДМНК для каждого отдельного структурного уравнения, не являются окончательными, а используются на третьем шаге для оценки структурных коэффициентов всей системы одновременно.
Таким образом, процедура оценки коэффициентов структурной формы всей системы взаимозависимых эконометрических моделей состоит из трех последовательных этапов, определяющих содержание ТМНК.
Шаг 1. На данном этапе с использованием обычного МНК на основании приведенной формы определяются расчетные значения переменных 
, рассматриваемых в качестве независимых эндогенных переменных в каждом из уравнений системы.
Шаг 2. Как и в ДМНК, на этом этапе с использованием значений определяются оценки коэффициентов структурной формы каждого из уравнений системы.
Шаг 3. С помощью обобщенного МНК определяются ”окончательные” оценки коэффициентов структурной формы всей системы взаимозависимых эконометрических моделей, которые теоретически при наличии корреляции между ошибками различных уравнений являются “более эффективными” по сравнению с аналогичными оценками ДМНК.
Если ошибки системы не коррелируют между собой, то ТМНК не имеет преимуществ перед двухшаговым. При применении ТМНК необходимо соблюдать некоторые дополнительные правила, что делает его процедуру менее универсальной по сравнению с двухшаговой. Они состоят в следующем.
1. Процедура выполняется только для идентифицируемых и сверхидентифицируемых уравнений системы. Тождества и неидентифицируемые уравнения в ней не участвуют.
2. Процедуру желательно выполнять для групп идентифицируемых и неидентифицируемых уравнений раздельно. При этом если в соответствующую группу входит только одно сверхидентифицируемое уравнение, то трехшаговая процедура для него превращается в двухшаговую.
Практическое применение трехшагового метода ограничено из-за большого количества расчетов и чрезвычайной чувствительности результатов к ошибкам спецификации.
Вопросы для самопроверки
1. Для каких систем одновременных уравнений применяют двухшаговый метод наименьших квадратов?
2. Назовите основные этапы ДМНК.
42. Эконометрические модели из одновременных уравнений. Точно идентифицированное и сверхидентифицированное уравнение модели (на примере расширенной «паутинной» модели спроса-предложения товара на конкурентном рынке).
Уравнения системы независимых уравнений могут рассматриваться самостоятельно в произвольном порядке, то есть к каждому их них применимы все операции, которые мы рассматривали выше для линейных уравнений.
Если зависимая (исследуемая переменная) одного уравнения выступает в качестве факторных переменной в последующих уравнениях, то может быть построена модель в виде системы линейных рекурсивных уравнений:
. (4.2)
Уравнения системы рекурсивных уравнений также могут рассматриваться по отдельности. В случае системы линейных уравнений параметры модели могут определяться с помощью МНК. При выполнении прогнозных значений необходимо будет производить вычисления последовательно, начиная с первого уранвения.
Наибольшее распространение в эконометрических исследованиях получила система одновременных (взаимозависимых) уравнений. В ней одни и те же зависимые (исследуемые) переменные в одних уравнениях входят в левую часть, а других – в правую часть системы. Даже в простейшем случае системы одновременных линейных уравнений (eё также называют структурной формой модели – СФМ) :
определение параметров модели сталкивается с большими трудностями и не всегда возможно в принципе. Для нахождения параметров модели исходная система одновременных линейных уравнений сводится кприведённой форме модели (ПФМ), которая имеет вид системы независимых переменных:
Такое сведение всегда возможно произвести с помощью алгебраических преобразований исходной системы уравнений. Параметры приведённой системы δij можно находить с помощью МНК. Основная трудность заключается в том, что не всегда возможно по коэффициентам приведённой системы восстановить коэффициенты исходной системы уравнений, то есть осуществить обратный переход (подобно тому, как мы это делали, сводя нелинейное уравнение к линейному, находя параметры линейной модели, а затем производя обратный пересчёт параметров нелинейной модели).
Проблема перехода от приведённой формы (ПФМ) системы уравнений к исходной СФМ называется проблемой идентификации. Различаются идентифицируемые, неидентифицируемые и сверхидентифицируемые модели.
1. Модель идентифицируема, если все коэффициенты исходной модели определяются однозначно, единственным образом по коэффициентам приведённой модели. Это возможно когда число параметров исходной модели равно числу параметров приведённой формы (здесь и далее не учитывается число свободных коэффициентов в уравнениях). Процедура нахождения коэффициентов идентифицируемой модели носит название косвенного метода наименьших квадратов (КМНК) и содержит следующие этапы:
а) исходная модель преобразуется в приведённую форму модели;
б) для каждого уравнения приведённой формы модели применяется обычный МНК;
в) коэффициенты приведённой модели трансформируются в коэффициенты исходной модели.
2. Модель неидентифицируема, если число параметров приведённой системы меньше чем, число параметров исходной модели, и в результате коэффициенты исходной модели не могут быть оценены через коэффициенты приведённой формы.
3. Модель сверхидентифицируема, если число приведённых коэффициентов больше числа коэффициентов в исходной модели. В этом случае на основе коэффициентов приведённой формы можно получить два и более значений одного коэффициента исходной модели. Сверхидентифицируемая модель в отличие от неидентифицируемой модели практически разрешима, но требует специальных методов исчисления параметров. Наиболее распространённым является двух шаговый метод наименьших квадратов (ДНМК). Основная идея ДНМК – на основе приведённой формы модели получить для сверхидентифицируемого уравнения (имеются критерии для определения идентифицируемости каждого уравнения исходной системы) теоретические значения исследуемых переменных, содержащегося в правой части уравнения. Далее, подставив эти значения вместо фактических значений (результатов наблюдений), применяется МНК к сверхидентифицируемому уравнению исходной системы.
Для того, чтобы модель была идентифицируема, необходимо, чтобы каждое уравнение модели было идентифицируемо. Если хотя бы одно уравнение СФМ неидентифицируемо, то вся модель считается неидентифицируемой.
Рассмотрим необходимые и достаточные условия идентифицируемости отдельного уравнения модели.
Необходимым условием идентифицируемости отдельного уравнения модели является счетное правило. Если обозначить через Н число исследуемых переменных yl, присутствующих в i-м уравнении, а через D обозначить число факторных переменных xj, отсутствующих в i-м уравнении, то счётное правило формулируется следующим образом:
— если D + 1 H, то уравнение сверхидентифицируемо.
Достаточное условие идентифицируемости отдельного уравнения модели выполняется, если определитель матрицы, составленной из коэффициентов в других уравнениях при переменных (как исследуемых y, так и факторных x), отсутствующих в данном i-м уравнении не равен нулю, а ранг этой матрицы, одновременно, не меньше, чем количество всех исследуемых переменных в системе уравнениё за вычетом 1.
Компонентный анализ является методом определения структурной зависимости между случайными переменными. В результате его использования получается сжатое описание малого объёма, несущее почти всю информацию, содержащуюся в исходных данных. Основой компонентного анализа является построение таких линейных комбинаций исходных переменных (главных компонент), которые бы имели максимальную дисперсию и минимальную зависимость друг от друга.
Более общим методом преобразования исходных переменных по сравнению с компонентным анализом является факторный анализ. Центральной проблемой, которую приходится решать при обработке экспериментальных данных, является задача её “сжатия”, выделения существенной информации, которая затемнена разного рода данными, не имеющими отношения к сути изучаемого явления. Поэтому задача уменьшения размеров исходного массива данных тесно связана с задачей выявления закономерностей изучаемого явления. Наблюдаемые параметры зачастую являются лишь косвенными характеристиками изучаемого объекта. На самом деле существуют внутренние (не наблюдаемые непосредственно) параметры или свойства, число которых мало и которые определяют значения наблюдаемых параметров. Эти внутренние параметры принято называть факторами. Задача факторного анализа – представить наблюдаемые параметры в виде линейных комбинаций факторов.
Видео:7 класс, 3 урок, Что такое математическая модельСкачать
Необходимое условие идентифицируемости
Чтобы уравнение было идентифицируемо, необходимо, чтобы число предопределенных переменных, отсутствующих в данном уравнении, но присутствующих в системе, было равно числу эндогенных переменных в данном уравнении без одного.
Введем следующие обозначения:
М – число предопределенных переменных в модели;
m— число предопределенных переменных в данном уравнении;
— число эндогенных переменных в модели;
— число эндогенных переменных в данном уравнении;
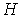
Обозначим число экзогенных (предопределенных) переменных, которые содержатся в системе, но не входят в данное уравнение через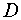 
, 
.
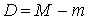
Тогда условие идентифицируемости каждого уравнения модели может быть записано в виде следующего счетного правила:
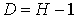 | уравнение идентифицируемо |
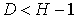 | уравнение неидентифицируемо |
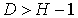 | уравнение сверхидентифицируемо |
Для оценки параметров структурной модели система должна быть идентифицируема или сверхидентифицируема.
Рассмотренное счетное правило отражает необходимое, но недостаточное условие идентификации.
Достаточное условие идентификации
Уравнение идентифицируемо, если по отсутствующим в нем переменным (эндогенным и экзогенным) можно из коэффициентов при них в других уравнениях системы получить матрицу, определитель которой не равен нулю, а ранг матрицы не меньше, чем число эндогенных переменных в системе без одного.
Целесообразность проверки условия идентификации модели через определитель матрицы коэффициентов, отсутствующих в данном уравнении, но присутствующих в других, объясняется тем, что возможна ситуация, когда для каждого уравнения системы выполнено счетное правило, а определитель матрицы названных коэффициентов равен нулю. В этом случае соблюдается лишь необходимое, но не достаточное условие идентификации.
В эконометрических моделях часто наряду с уравнениями, параметры которых должны быть статистически оценены, используются балансовые тождества переменных, коэффициенты при которых равны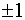 
. В этом случае, хотя само тождество и не требует проверки на идентификацию, ибо коэффициенты при переменных в тождестве известны, в проверке на идентификацию структурных уравнений системы тождества участвуют..
Изучается модель (одна из версий модели Кейнса):
(7.8)
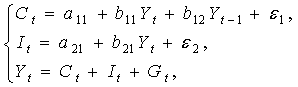
где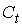 
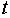
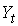
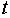
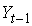
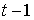
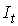
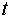
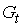
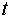
– потребление в период 
; 
– ВВП в период ; 
— ВВП в период ( 
); 
– валовые инвестиции в период 
; 
– государственные расходы в период .
Первое уравнение – функция потребления, второе уравнение – функция инвестиций, третье уравнение –тождество ВВП. Модель представляет собой систему одновременных уравнений. Проверим каждое ее уравнение на идентификацию.
Модель включает три эндогенные переменные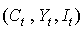 
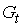
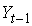
и две предопределенные переменные (одна экзогенная переменная – и одна лаговая переменная – ).
Проверим необходимое условие идентификации для каждого из уравнений модели.
| N | Уравнение | 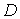 | счетное правило |
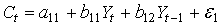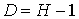 |  | идентифицируемо | |
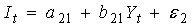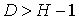 |  | сверхидентифицируемо | |
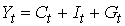 | тождество, не подлежит проверке |
Например, первое уравнение содержит две эндогенные переменные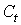 
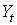
и 
и одну предопределенную переменную 
.
Таким образом,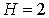 
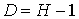
; D=2-1=1. Условие условие выполняется, т. е. уравнение идентифицируемо.
Проверим для каждого уравнения достаточное условие идентификации. Для этого составим матрицу коэффициентов при переменных модели.
| | | |  | | |
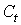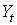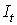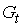| I уравнение | -1 | b11 | b12 | 0 | 0 |
| II уравнение | 0 | b21 | 0 | -1 | 0 |
| Тождество | 1 | 0 | 0 | 1 | 1 |
В соответствии с достаточным условием идентификации ранг матрицы коэффициентов при переменных, не входящих в исследуемое уравнение, должен быть равен числу эндогенных переменных модели без одного.
Первое уравнение: матрица коэффициентов при переменных, не входящих в уравнение, имеет вид: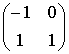 
. Ее определитель не равен нулю, поэтому ранг матрицы равен 2, т. е равняется числу эндогенных переменных без одного. Достаточное условие идентификации выполняется.
Второе уравнение: матрица коэффициентов при переменных, не входящих в уравнение, имеет вид: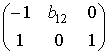 
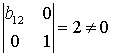
. Ранг данной матрицы равен 2, так как существут определитель второго порядка не равный нулю: 
. Следовательно, достаточное условие идентификации для данного уравнения также выполняется Но в соответствии с необходимым условием считаем это уравнение сверхидентифицируемым.
Таким образом, эта система уравнений является сверхидентифицируемой.
7.5. Методы оценки параметров структурной формы модели
Коэффициенты структурной модели могут быть оценены разными способами в зависимости от вида системы одновременных уравнений. Наибольшее распространение в литературе получили следующие методы оценивания коэффициентов структурной модели:
1) косвенный метод наименьших квадратов;
2) двухшаговый метод наименьших квадратов;
3) трехшаговый метод наименьших квадратов;
4) метод максимального правдоподобия с полной информацией;
5) метод максимального правдоподобия при ограниченной информации.
Рассмотрим сущность некоторых из этих методов.
Косвенный метод наименьших квадратов (КМНК) применяется в случае точно идентифицируемой структурной модели. Процедура применения КМНК предполагает выполнение следующих этапов:
1. Для структурной модели строится приведенная форма модели.
2. Для каждого уравнения приведенной формы традиционным МНК оцениваются приведенные коэффициенты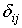 
.
3. На основе коэффициентов приведенной формы находятся путем алгебраических преобразований параметры структурной модели.
Двухшаговый метод наименьших квадратов (ДМНК)
Если система сверхидентифицируема, то КМНК не используется, ибо он не дает однозначных оценок для параметров структурной модели. В этом случае могут использоваться разные методы оценивания, среди которых наиболее распространенным и простым является двухшаговый метод (ДМНК).
Основная идея ДМНК состоит в следующем:
· на основе приведенной формы модели получить для сверхидентифицируемого уравнения расчетные значения эндогенных переменных, содержащихся в правой части этого уравнения;
· подставляя найденные расчетные значения эндогенных переменных вместо фактических значений, можно применить обычный МНК к структурной форме сверхидентифицируемого уравнения.
Метод получил название двухшагового МНК, ибо дважды используется МНК:
· на первом шаге при определении параметров приведенной формы модели и нахождении на их основе оценок расчетных значений эндогенных переменных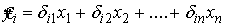 
; 
;
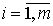
· на втором шаге применительно к структурному сверхидентифицируемому уравнению, когда вместо фактических значений эндогенных переменных рассматриваются их расчетные значения, найденные на предыдущем шаге.
Сверхидентифицируемая структурная модель может быть двух типов:
· все уравнения системы сверхидентифицируемы;
· система содержит наряду со сверхидентифицируемыми точно идентифицируемые уравнения.
Если все уравнения системы сверхидентифицируемые, то для оценки структурных коэффициентов каждого уравнения используется ДМНК. Если в системе есть точно идентифицируемые уравнения, то структурные коэффициенты по ним можно найти на основе косвенного МНК. Двухшаговый метод, примененный к точно идентифицированным уравнениям дает такой же результат, что и косвенный МНК.
Продолжение примера 15.
Продолжим рассмотрение примера 15.
Система является сверхидентифицируемой: первое уравнение идентифицируемо, а второе уравнение сверхидентифицируемо. Поэтому для определения коэффициентов первого уравнения можно применить косвенный МНК, а для второго уравнении двухшаговый МНК.
Построим приведенную форму модели:
(7.9)
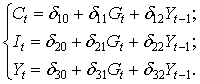
Исходные данные задачи (в млрд. руб.)
| годы | 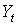 | 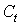 | 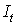 | 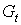 | 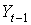 | Предсказанное |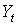
| 4823.23 | 2281.18 | 670.44 | 2629.62 | 4182,05 | ||
| 7305.65 | 3009.42 | 1165.23 | 1014.2 | 4823.23 | 6731,57 | |
| 8943.58 | 3972.81 | 1504.71 | 1193.5 | 7305.65 | 9496,45 | |
| 10830.54 | 5001.77 | 1762.41 | 1947.3 | 8943.58 | 11692,48 | |
| 13243.24 | 6147.26 | 2186.37 | 2345.6 | 10830.54 | 13947,4 | |
| 17048.12 | 7670.68 | 2865.01 | 2659.4 | 13243.24 | 16716,24 | |
| 21625.37 | 9613.84 | 3611.11 | 3472.1 | 17048.12 | 21268,68 | |
| 26903.49 | 11927.59 | 4730.02 | 4284.8 | 21625.37 | 26648,73 | |
| 33258.14 | 14831.38 | 6716.22 | 26903.49 | 33297,77 |
Найдем параметры модели (7.9), применяя МНК к каждому уравнению,
используем « Пакет анализа» EXCEL):
(7.10)
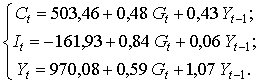
Каждое уравнение статистически значимо (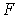 
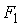
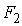
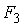
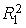
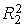
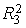
– статистики: 
=1302,55;
=281,956; 
=847,65). Коэффициенты детерминации свидетельствуют о хорошей связи между эндогенными и предопределенными переменными: 
=0,9977; 
=0,989; 
=0,996.
На основе уравнений модели (7.10) найдем структурные коэффициенты первого уравнения.
Выразим из третьего уравнения (7.10) переменную 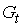и подставим в первое уравнение. Получим первое структурное уравнение: 
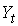
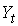
Так как второе уравнение сверхидентифицировано, то применим двухшаговый МНК. Найдем на основе третьего уравнения (7.10) расчетные значения переменной ( столбец «предсказанное » табл.23) и используем их для нахождения параметров второго структурного уравнения.
Получим: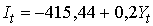 
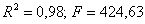
4; 
.
В результате получим следующую систему структурных уравнений:
Трехшаговый метод наименьших квадратов (ТМНК)
Трехшаговый метод наименьших квадратов применяется для оценки параметров системы одновременных уравнений в целом. Сначала к каждому уравнению применяется двухшаговый метод с целью оценить коэффициенты и случайные остатки каждого уравнения. Затем строится ковариационная матрица остатков и проводится ее оценка. После этого для оценивания коэффициентов всей системы применяется обобщенный метод наименьших квадратов. ТМНК является достаточно эффективным, но требует существенно больших вычислительных затрат. Более подробное описание можно найти в работе[1][1]
🎬 Видео
Математика 5 класс. Математическая модельСкачать
Урок 9 класс. Системы уравнений как математические модели реальных ситуаций.Скачать
Тихонов Н. А. - Основы математического моделирования - Типы математических моделей (Лекция 1)Скачать
Алгебра 9 класс. Системы уравнений как математические модели реальных ситуацийСкачать
Дамми (фиктивные) переменные. Разные зависимости для подвыборокСкачать
Алгебра 7 класс. 7 сентября. Что такое математическая модельСкачать
Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать
Решить интегральное уравнение (ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ) Свёртка функций, Умножение изображенийСкачать
Математическая модель задачи. Как составить. Математическая постановка. Исследование операций.Скачать
Показательная зависимость 4. Функциональное уравнениеСкачать
Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать
Математическая модель. Видеоурок по алгебре 7 классСкачать
Математическое моделированиеСкачать
Структурные модели реологических средСкачать
УРОК 25. Модели и виды моделей (9 класс)Скачать
