Точки разрыва функции решение уравнений

Видео:Математика без Ху!ни. Непрерывность функции, точки разрыва.Скачать

Как найти точки разрыва функции — пошаговая инструкция

Нахождение точек разрыва функции является одним из обязательных моментов исследования на непрерывность. Для кого-то это может прозвучать непонятно, а для остальных будет слишком банально.

Но и тем, и другим не стоит делать поспешные выводы: материал этой темы действительно предельно прост, но вместе с тем для успешного решения практических задач потребуется осмыслить и запомнить несколько технических приемов и нюансов.

Как минимум необходимо понимать, что за «зверь» кроется под понятием предела функции. И конечно же, нужно уметь их решать. Не менее полезным станет понимание геометрического смысла, дополненное графиком — большинство задач подобного характера требуют построения чертежа после решения.

Видео:Точки разрыва функции #2Скачать

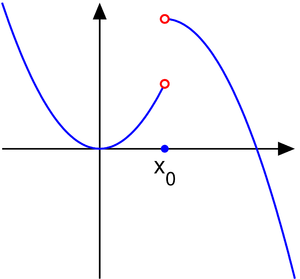
Определение точки разрыва

Как уже упоминалось, их поиск напрямую связан с темой непрерывности. Если говорить простым языком, то это не что иное, как координаты графика функции, в которых точки не соединяются между собой. Образуются «рваные области», которые и называют местом разрыва. Вообще, чтобы понять смысл, достаточно всего лишь взглянуть на рисунок:

Он более чем очевидно иллюстрирует определение понятия. Если функция прерывается в X0, то непрерывность в этом месте нарушена одним из двух возможных способов:

Задачи похожего типа, где необходимо находить точки разрыва, могут выступать не только, как один из этапов полного исследования на непрерывность, но и в качестве самостоятельных заданий. Чтобы определить их вид, потребуется отыскать предел для найденных значений. Поэтому, если вы еще не умеете их решать, самое время ненадолго отвлечься, чтобы изучить базовые основы.

К счастью, на практике это не так сложно — самый трудный этап заключается в приведении примера к одному из табличных. Остальные моменты легко запомнить. Не стоит забывать и о большом количестве сервисов, которые в несколько кликов выдадут значение предела любой сложности онлайн.

Классификация точек разрыва.

Видео:Непрерывность функции и точки разрыва функцииСкачать

Точки разрыва первого и второго рода

Если функция не определена, но односторонние пределы имеют конечное значение, то ее относят к случаю первого рода. Который, в свою очередь, может иметь характеристику устранимого или конечного:

Точки устранимого разрыва функции. Значения вычислений обоих пределов для них равны. Но также имеется возможность «исправить ситуацию»: нахождения между двумя координатами такой, левый и правый пределы которой будут одинаковы, а сама она — соединит «порванный» участок, сделав график непрерывным.

Точки конечного разрыва первого рода — скачок функции. Пределы могут быть вычислены, но в то же время не равны друг другу, и поэтому доопределение уравнения невозможно. Разница первого и второго называется скачком.

Видео:✓ Точки разрыва. Функции Дирихле и Римана. Разрывы монотонных функций | матан #021 | Борис ТрушинСкачать

Как найти точки разрыва функции

Если в условиях задачи не были даны координаты проверяемого отрезка, то процесс решения делится на несколько этапов. Для начала нужно найти область определенных значений, с которой в дальнейшем пойдет работа. После это вычисляются односторонние пределы функции. Полученные результаты необходимо будет сравнить, чтобы однозначно определить род и характеристику разрыва.

Рассмотрим более подробно каждый из этих моментов на примере нахождения нужных нам точек у конкретного примера f (y)=(y² — 25)/(y — 5):

1. Областью определения называют множество значений, в котором существует функция. Здесь не нужны никакие сложные вычисления, достаточно взять лишь знаменатель. Если y=5, то он будет (5−5)=0 и, как всем известно, делить на него нельзя. Таким образом, получаем область допустимых y ∈ (-∞; 5) ∪ (5; +∞) и предполагаем, что наша y = 5 является точкой разрыва.
2. Вычисление односторонних пределов. Это самая сложная для учеников часть, т. к. пределы не всегда бывают удобными для вычисления, да не все на них «собаку съели». Но в этом случае функцию можно значительно упростить еще до начала вычисления: f (y) = (y ²-25)/(y — 5) = ((y-5)(y+5)) /(y — 5) = y+5. Никогда не пренебрегайте такой возможностью, если она есть. Заметим, что новая функция непрерывна при любом численном значении, т. ч. по всем математическим правилам пределы будут равны: lim (y + 5) = 5 + 5 = 10.
3. Проверяя совпадение результатов, мы выяснили, что левый и правый предел функции в точке y=5 одинаковые. Но вместе с тем функция f(y) не может быть определена в этой координате, иначе ее знаменатель обращается в ноль, что невозможно по условиям. Следовательно, она действительно является разрывом, а именно: устранимым и первого рода.

Видео:Исследовать точки разрыва функции (непрерывность)Скачать

Видео

Из этого видео вы узнаете, как исследовать непрерывность функции.

Видео:Математический анализ, 5 урок, Непрерывность функцииСкачать

Точки разрыва функции онлайн

Функция является непрерывной в некоторой точке , если выполняются следующие условия:

Т.е. предел функции при стремлении (слева), равен пределу функции при стремлении (справа) и равен значению функции в точке .

Если хотя бы одно из условий нарушается, тогда говорят, что функция имеет разрыв в точке .

Все точки разрыва функции делят на точки разрыва первого рода и точки разрыва второго рода.

Eсли существуют конечные односторонние пределы и , тогда точка называется точкой разрыва первого рода.

Точки разрыва первого рода в свою очередь подразделяются на точки устранимого разрыва и скачки.

Если — является точкой разрыва первого рода и при этом , точка называется точкой устранимого разрыва.

График соответствующей функции приведён на рисунке ниже:

Eсли же , тогда в точке . происходит скачок функции Величина скачка определяется по формуле . Соответствующий график приведён на рисунке:

Если хотя бы один из пределов или равен , точка называется точкой разрыва второго рода. Пример соответствующего графика функции представлен на рисунке ниже:

Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha вычисляет точки разрыва заданной функции с описанием подробного хода решения.

Видео:Найти точки разрыва функции (непрерывность)Скачать

Точки разрыва функции — алгоритмы и примеры решения

Нахождение точек разрыва функции является одним из важнейших элементов исследования в математическом анализе. Многие студенты используют для пополнения своих знаний информацию из интернета, однако даже не подозревают, что она может быть недостоверной. Чтобы избежать неприятных последствий, следует решать по методике, которую рекомендуют специалисты, а также обладать определенными базовыми знаниям.

Видео:Точки разрыва функции // Высшая МатематикаСкачать

Общие сведения

Функцией называется зависимость одной переменной от другой. Если записать ее в виде равенства w = f (p), то величина «w» зависит от «р». Первая называется значением функциональной зависимости, а вторая — ее аргументом. Последний может принимать любые значения, кроме превращающих «w» в пустое множество. Примером является выражение w = [(p — 2)(p + 7)] / (p 2 — 1). При значениях р1 = -1 и р2 = 1 получается пустое множество, поскольку на нуль делить нельзя.

Когда математики говорят, что нужно произвести исследование функции на непрерывность, т. е. необходимо найти точки разрыва первого и второго рода. Если же таковых нет, то данное утверждение следует доказать математическим методом.

Непрерывной называется функция, которая не имеет точек разрыва, и меняется без существенных скачков в некоторых точках или промежутках, т. е. обладает определенным знакопостоянством. Это свойство определяется при помощи метода, представляющего совокупность математических преобразований. Последние основываются на теоремах. Они позволяют доказать существование или отсутствие точек и интервалов разрыва графика функции.

Видео:Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать

Базовые знания

Базовые знания — совокупность навыков, необходимых для решения какой-либо задачи. Для нахождения точек разрыва необходимы такие знания:

• Область определения — D.
• Решение уравнений.
• Нахождение пределов при известных значениях левосторонней и правосторонней границ.
• Классификация точек разрыва.

Когда список сформирован, тогда необходимо приступать к изучению материала. После полного понимания первого пункта необходимо переходить к последующему. Все пять элементов связаны между собой. Специалисты рекомендуют не заучивать наизусть понятия и термины, а понимать их.

Область определения

Областью определения некоторой функции w = f (p) называется интервал или числовой промежуток всех значений аргумента «р», при которых существует эта функция. Величину следует обозначать литерой «D». Конечная запись для вышеописанного тождества имеет такой вид: D (w) или D (f (р)).

Следует отметить, что D (w) зависит от ее вида. В алгебре бывают только простые и составные. К первым нужно отнести следующие подтипы:

• Алгебраические: рациональные (целые и дробные) и иррациональные (знак радикала).
• Тригонометрические (sin, cos, tg, ctg и производные от них).
• Трансцендентные (степенные, показательные и логарифмические).

К рациональным равенствам целого типа относятся любые выражения без корней, степеней, дробей, логарифмов, а также тождества, не содержащие каких-либо тригонометрических функций. В этом случае D соответствует всему интервалу действительных, которые обозначаются литерой «Z».

Для дробных D (w) зависит от знаменателя. В этом случае нужно решить уравнение, приравняв знаменатель к нулю. Например, чтобы найти D у функции вида w = [(p — 2)(p + 7)] / (p 2 — 1), нужно приравнять знаменатель дроби к 0.

Когда выражение является иррациональным, тогда нужно обратить внимание на степень корня и подкоренное выражение. Если степень четная, то выражение не должно быть отрицательным числом. Функция действительна для всех Z, кроме тех, которые превращают выражение под корнем в пустое множество. Например, для w = (p — 2) / [(p 2 — 1)]^(½) нужно решить неравенство (p 2 — 1) > 0. Интервалы, которым соответствует решение, можно записать в таком виде: (-бесконечность;-1) U (1;бесконечность). Бесконечность можно еще обозначать «inf».

Выражение под натуральным логарифмом должно быть всегда больше 0. В этом случае решается также неравенство, состоящее из тождества, находящегося под его знаком. Интервал для косинуса и синуса — все Z. Однако для tg (x) рекомендуется исключить значения аргумента (Pi / 2) + Pi * k, а для и ctg (x) — Pi * k (к принадлежит множеству Z).

Решение уравнений

Уравнения бывают нескольких видов: линейными, квадратными, кубическими и биквадратными. Первые являются самыми простыми, и решаются при помощи такой методики:

• Выполнение математических преобразований, упрощающих выражение.
• Перенос неизвестных в одну, а известных — в другую часть.
• Определение неизвестной.

К квадратным относятся равенства вида ap 2 + bp + c = 0. Математики их классифицируют на неполные и полные. К первым относятся только равенства, которые не содержат второй или третий член. Квадрат при первом коэффициенте должен быть всегда. Существует 4 метода решения:

• Если а = 1, то решается по теореме Виета.
• Использование дискриминанта.
• Разложение на множители.
• Построение графика.
• Использование программного обеспечения.

В первом случае нахождение корней осуществляется с помощью двух формул: р1 + р2 = -b и р1 * р2 = с. Однако при а > 1 нужно воспользоваться формулой для расчета некоторого вспомогательного параметра. Он называется дискриминантом (D). Для решения уравнения по второй методике рекомендуется применять такой алгоритм:

Рассчитать D по формуле: D = b 2 — 4ac.

Корни: t1 = -1 и t2 = 5/2.

Следовательно, 2t 2 — 3t — 5 = (t + 1) * (2t — 5). После разложения нужно вычислить предел: lim [((t + 1) * (2t — 5)) / (t + 1)] | (t -> -1) = lim [2t — 5] | (t -> -1) = [2* (-1) — 5] = -2 — 5 = -7. Уравнения могут объединяться в системы.

Виды разрывов

Чтобы исследовать функцию на непрерывность, нужно уметь определять характер разрыва. Он классифицируется следующим образом: первого и второго рода. Первые бывают двух типов: устранимые и неустранимые.

Разрыв I рода существует в том случае, когда оба предела (левосторонний и правосторонний) являются конечными, т. е. не равны inf. Когда оба предела равны, то это точка устранимого разрыва. В противном случае (при неравенстве односторонних пределов) — разрыв является неустранимым, и называется «скачком».

Возможен вариант, когда один из пределов эквивалентен бесконечности. В этом случае говорят, что это разрыв II рода. Запись левого и правого пределов имеет такой вид: p -> -5 — 0 и p -> -5 + 0 соответственно.

Видео:Исследовать непрерывность функции (точки разрыва)Скачать

Решения задач

После получения базовых знаний необходимо разобрать примеры решения. Точки разрыва функции следует искать по следующему алгоритму:

Если выполнить такой же расчет для правосторонней границы, то ее значение будет соответствовать левосторонней.

Выполнять вычисления для двух точек необязательно, поскольку пределы будут равны и в этом случае. Следовательно, это устранимый разрыв I рода.

Таким образом, для нахождения разрывов необходимо знать некоторые особенности и методику, позволяющую правильно классифицировать их характер.

📽️ Видео

Непрерывность функции и точки разрываСкачать

Примеры исследования функций на непрерывностьСкачать

Математика без Ху!ни. Нахождение асимптот, построение графика функции.Скачать

Точки разрыва функцииСкачать

Точки разрыва функцииСкачать

Матан. Пределы для успешной сдачи зачёта | TutorOnline МатематикаСкачать

26. Односторонние пределы функции в точке / определение /примерыСкачать

Точки разрыва функцийСкачать

Классификация точек разрываСкачать

Непрерывность функции, точки разрываСкачать