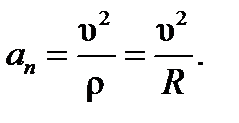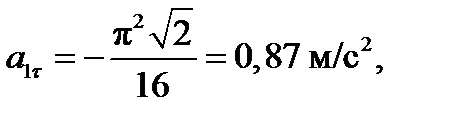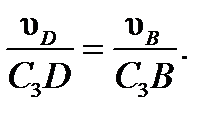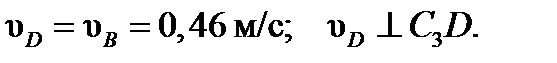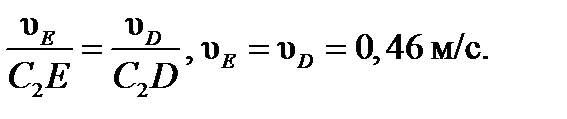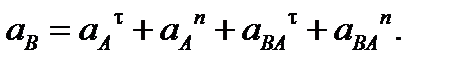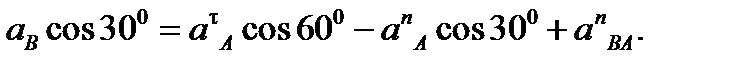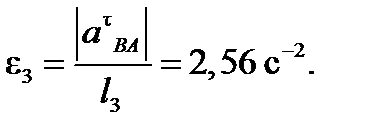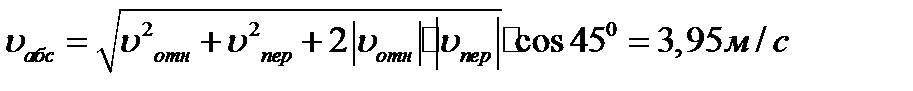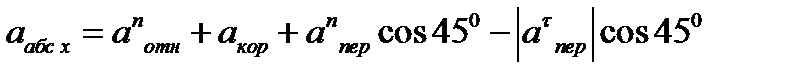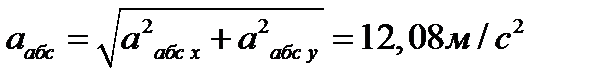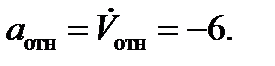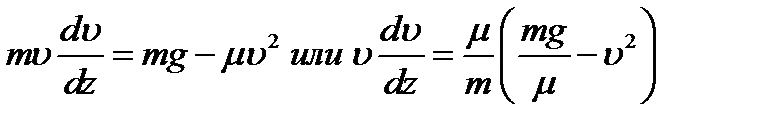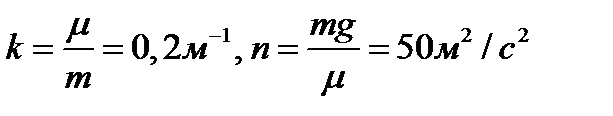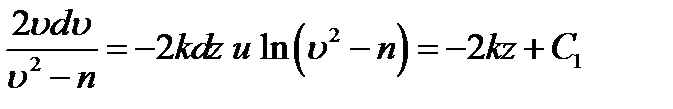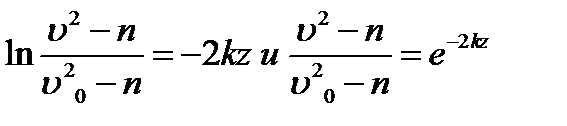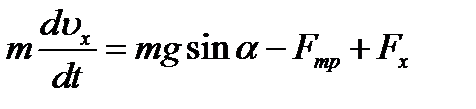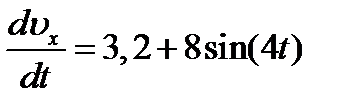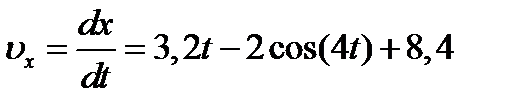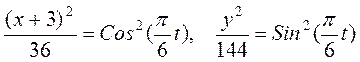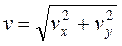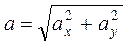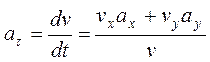Точка В движется в плоскости ху(рис. К1.0 – К1.9, табл.К1; траектория точки на рисунках показана условно). Закон движения точки задан уравнениями: х = f2 (t),y = f2 (t), где хи увыражены в сантиметрах, t– в секундах.
Найти уравнение траектории точки; для момента времени t1 =1сопределить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
Зависимость x = f1 (t) указана непосредственно на рисунках, а зависимость y = f2 (t) дана в табл.К1 (для рис. 0-2 в столбце 2, для рис. 3-6 в столбце 3, для рис. 7-9 в столбце 4).
Указания. Задача К1 относится к кинематике точки и решается с помощью формул, по которым определяются скорость и ускорение точки в декартовыхкоординатах (координатный способ задания движения точки), а также формул, по которым определяются касательное и нормальное ускорение точки.
В данной задаче все искомые величины нужно определить только для момента времени t1 = 1c. В некоторых вариантах задачи при определении траектории или при последующих расчетах (для их упрощения) следует учесть известные из тригонометрии формулы:
cos2a = 1 – 2sin 2 a =2cos 2 α –1,
sin2a = 2sina× cos a
Рис. К1.0-9
 |
Пример К1.Даны уравнения движения точки в плоскости ху:

(х,у – в сантиметрах, t – в секундах).
Определить уравнение траектории точки; для момента времени t1 = 1с найти скорость и ускорение точки, а также ее касательное и нормальное ускорение и радиус кривизны в соответствующей точке траектории.
Решение. 1. Для определения уравнения траектории точки исключим из данных уравнений движения время t.
Таблица К1
| № условия | У = f2 (t) | |
| Рис. 0 – 2 | Рис. 3 — 6 | Рис. 7 — 9 |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 | 2t 3 |  |
 |  |  |
Поскольку t входит в аргументы тригонометрических функций, где один аргумент вдвое больше другого, используем формулу
Из уравнений движения находим выражения соответствующих функций и подставляем в равенство (1). Получим
следовательно,
Откуда окончательно находим следующее уравнение траектории точки (парабола, рис.К1):

проекциям на координатные оси:
|

3. Аналогично найдем ускорение точки:



4. Касательное ускорение найдем, дифференцируя по времени равенство



Числовые значения всех величин, входящих в правую часть выражения (5), определены и даются равенствами (3) и (4). Подставив сюда эти числа, найдем сразу, что при t1 =1c, a1t =0,66см/c 2 .
5. Нормальное ускорение точки 
6. Радиус кривизны траектории r =u 2 /an . Подставляя сюда числовые значения u1 и a1n , найдем, что при t1 = 1c r1 = 3,05см.
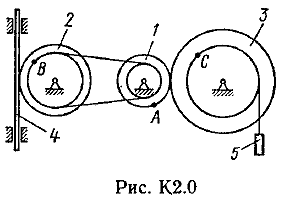
Плоский механизм состоит из: колёс 1, 2 и 3, планки 4 и груза 5. Диски и груз соединены между собой нерастяжимыми нитями. Диски, касающиеся планки, при движении механизма не проскальзывают.
Схемы механизмов показаны на рис. К2.0-9, необходимые для расчёта данные помещены в таблице К2.
| Дано | Найти | |||||||
| № условия | уравнение движения груза |  |  |  |  |  | скорости | ускорения |
| см | см | см | см | см | с | |||
 |  , ,   |  , ,  , ,  | ||||||
 |  , ,   |  , ,  , ,  | ||||||
 |  , ,   |  , ,  , ,  | ||||||
 |  , ,  |  , ,  , ,  | ||||||
 |  , ,  |  , ,  , ,  | ||||||
 |  , ,  |  , ,  , ,  | ||||||
 |  , ,   |  , ,  , ,  | ||||||
 |  , ,  |  , ,  , ,  , , | ||||||
 |  , ,   |  , ,  , ,  | ||||||
 |  , ,   |  , ,  , ,  |
По заданному направлению поступательного движения груза 5 определить в заданной момент времени угловые скорости и ускорения тел и линейные скорости и ускорения точек, указанных в таблице К2.
Указания. Студенту при решении задач следует учесть следующее. 1. Что скорости точек контакта тел, находящихся в зацеплении, равны между собой. 2. Два вращающихся тела связаны нерастяжимой ременной передачей, и скорости точек ремня равны скоростям соприкасающихся с ним точек тел. 3. Тело 1 представляет собой ступенчатое колесо с радиусами : 


Рис. К2.0-9
Пример К2.Груз 5 подвешен на нерастяжимой нити, намотанной на большую ступень колеса 1. Движение груза задано уравнением: 



 Рис. К2.10 Рис. К2.10 | Определить скорости точек  и Е и Е  , ,   , ускорения точки Е и рейки 4 , ускорения точки Е и рейки 4  , ,  , а также угловую скорость колеса 1 , а также угловую скорость колеса 1  и угловое ускорение колеса 2 и угловое ускорение колеса 2  в момент времени в момент времени  = 2 с. Решение Обозначим точки контакта взаимодействующих тел через K, L, M, D, E. Груз 5 опускаясь приводит во вращательное движение колесо 1. Скорость точки K контакта колеса и нити равна скорости груза, т. е. = 2 с. Решение Обозначим точки контакта взаимодействующих тел через K, L, M, D, E. Груз 5 опускаясь приводит во вращательное движение колесо 1. Скорость точки K контакта колеса и нити равна скорости груза, т. е.  . Вектор скорости . Вектор скорости  направлен в сторону увеличения координаты направлен в сторону увеличения координаты  , вектор , вектор  — по касательной к окружности радиуса — по касательной к окружности радиуса  . Искомая угловая скорость колеса 1 — . Искомая угловая скорость колеса 1 —  . . |
Чтобы определить скорость точки 






Зубчатая рейка 4 связана с колесом 2 и 1, как показано на рисунке К2.10, и движется в направляющих поступательно. Линейные скорости точек 






Ускорение планки 






Тогда, угловая скорость колеса 2 








Таким образом 
Вектор 






Подставляя в найденные аналитические выражения заданное значения параметра 








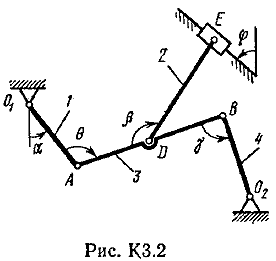
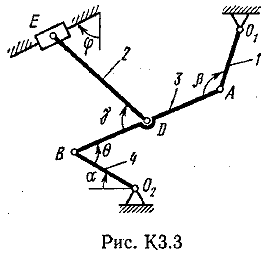
Плоский механизм состоит из стержней 1, 2, 3, 4 и ползунов В и Е(рис.К3.0.–7) или из стержней 1, 2, 3 и ползунов В и Е (рис К3.8-9), соединенных друг с другом и с неподвижными опорами О1, О2шарнирами; точка D находится в середине стержня АВ. Длины стержней равны соответственно : l1 =0,4м, l2 = 1,2 м, l3 =1,4м, l4 = 0,6м. Положение механизма определяется углами a, b, g, j, q. Значения этих углов и других заданных величин указаны в табл.К3.1 (для рис. К3.0 –4) или в табл.К3.2 (для рис.К3.5–9). Определить величины, указанные в таблицах в столбцах «Найти».
Дуговые стрелки на рисунках показывают, как при построении чертежа механизма должны откладываться соответствующие углы: по ходу или против хода часовой стрелки (например, угол g на рис. К2.8 следует отложить от DB по ходу часовой стрелки, а на рис. К2.9 – против часовой стрелки).
 |
Рис. К3.0-9
Таблица К3.1 (к рис. К3.0-К3.4)
| Номер условия | Углы, градусы | Дано | Найти | |||||
| a | b | g | j | q | w1 рад/с | w2 рад/с | Скорости точек | w звена |
| — | В,Е | DE | ||||||
| — | A,E | AB | ||||||
| — | B,E | AB | ||||||
| — | A,E | DE | ||||||
| — | D,E | AB | ||||||
| — | A,E | AB | ||||||
| — | B,E | DE | ||||||
| — | A,E | DE | ||||||
| — | D,E | AB | ||||||
| — | A,E | DE |
Таблица К3.2 (к рис. К3.5-К3.9)
| Номер условия | Углы, градусы | Дано | Найти | |||||
| a | b | g | j | q | w1, рад/с | uВ, м/с | Скорости точек | w звена |
| — | B,E | AB | ||||||
| — | A,E | DE | ||||||
| — | B,E | AB | ||||||
| — | A,E | AB | ||||||
| — | B,E | DE | ||||||
| — | D,E | DE | ||||||
| — | B,E | DE | ||||||
| — | A,E | AB | ||||||
| — | B,E | DE | ||||||
| — | D,E | AB |
Указания. Построение чертежа начинать со стержня, направление которого определяется углом a. Заданную угловую скорость считать направленной против часовой стрелки, а заданную скорость 
Задача К3 – на исследование плоскопараллельного движения твердого тела. При ее решении для определения скоростей точек механизма и угловых скоростей его звеньев следует воспользоваться теоремой о проекциях скоростей двух точек тела и понятием о мгновенном центре скоростей, применяя эту теорему (или это понятие) к каждому звену механизма в отдельности.
Пример К3. Механизм (рис.К3.10) состоит из двух стержней 1,2,3,4 и ползуна В,соединенных друг с другом и неподвижными опорами О2 и О2шарнирами.
Дано: a = 60 0 , b =150 0 , g = 90 0 , j = 30 0 , q = 30 0 , AD = DB, l1= 0,4 м, l2 = 1,2 м, l3 = 1,4 м, w2 = 2 рад/c (направление w1 – против хода часовой стрелки). Определить: VВ, VЕ, ω2.
1. Строим положение механизма в соответствии с заданными углами (рис.К2.11); на этом рисунке изображаем все векторы скоростей.
2. Определяем 






Направление 
Рис. К2.10 Рис. К2.11
 |  |
Теперь, зная 




3. Определяем 








Чтобы вычислить C3 D и C3 B, заметим, что ∆ АС3 В – прямоугольный, так что острые углы в нем равны 30 0 и 60 0 , и что С3В = АB sin 30 0 = 0,5 AB =BD.
Тогда ∆ ВС3 D является равносторонним и С3 В = С3 D. В результате равенство (3) дает

Так как точка Е принадлежит одновременно стержню 4, вращающемуся вокруг О2, то 






Составив теперь пропорцию, найдем, что

4. Определяем 




Ответ: VB = 0,46 м /c; VЕ = 0,46 м / с; ω2 = 0,67 рад / c.


Направление 
Теперь, зная 




3. Определяем 








Чтобы вычислить C3 D и C3 B, заметим, что ∆ АС3 В – прямоугольный, так что острые углы в нем равны 30 0 и 60 0 , и что С3В = АB sin 30 0 = 0,5 AB =BD.
Тогда ∆ ВС3 D является равносторонним и С3 В = С3 D. В результате равенство (3) дает

Так как точка Е принадлежит одновременно стержню 4, вращающемуся вокруг О2, то 






Составив теперь пропорцию, найдем, что

4. Определяем 




Видео:Кинематика точки Задание К1Скачать

Задача К 1. Определение скорости и ускорения точки по заданным уравнениям движения.
Задача К 1а.
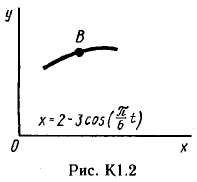
Точка В движется в плоскости ху (рис. К 1.0 – К 1.9, табл. К 1; траектория точки на рисунках показана условно). Закон движения точки задан уравнениями: х=f1(t), у=f2(t), где х и у выражены в сантиметрах, t – в секундах.
Найти уравнение траектории точки; для момента времени t1=1 с, определить скорость и ускорение точки, а также её касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
Зависимость х=f1(t) указана непосредственно на рисунках, а зависимость у=f2(t) дана в табл. К 1 (для рис. 0-2 в столбце 2, для рис. 3-6 в столбце 3, для рис. 7-9 в столбце 4). Как и в задачах C 1-С 4, номер рисунка выбирается по предпоследней цифре шифра; а номер условия в табл. К 1-по последней.
Задача К 1б.
Точка движется по дуге окружности радиуса R=2м по закону s=f(t), заданному в табл. К 1 в столбце 5 (s – в метрах, t – в секундах), где s=AM – расстояние точки от некоторого начала А, измеренное вдоль дуги окружности. Определить скорость и ускорение точки в момент времени t1=1 с. Изобразить на рисунке векторы υ и a, считая, что точка в этот момент находится в положении М, а положительное направление отсчета s-от А к М.
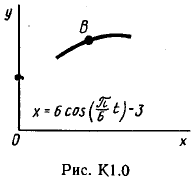 | 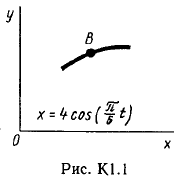 |  |
 |  |  |
 |  |  |
 |
Пример К 1а.По заданным уравнениям движения точки М в координатной форме определить: траекторию её движения в заданный момент времени t=1c, найти скорость и ускорение.


1. Определим траекторию движущейся точки М.
Для получения уравнения траектории движущейся точки исключим из заданных уравнений параметр времени t:


Полученные уравнения возведем в квадрат и суммируем:
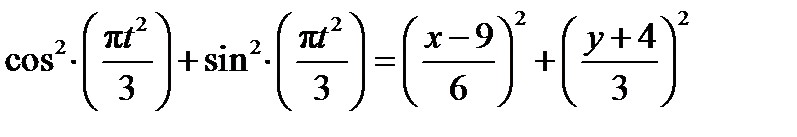
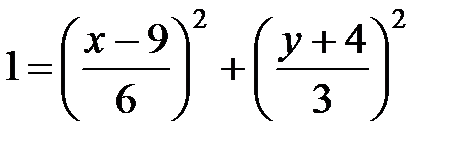
Данное выражение представляет собой траекторию движущейся точки М – уравнение эллипса с центром в точке с координатами (9; -4). Построим траекторию в координатных осях ху (рис.9).
Укажем положение точки М на траектории в заданный момент времени, для этого подставим время t=1с, в уравнения:
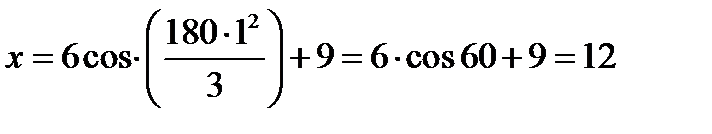

Тогда точка М с координаты (12; -1,4).
Для указания положительного отсчета по траектории определим положение точки М в начальный момент времени при t=0 с.
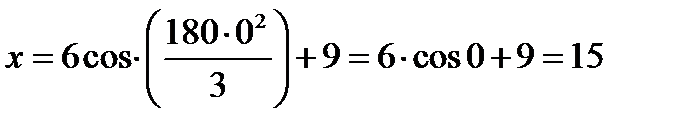

Тогда точка М0 имеет координаты (15; — 4).
Точки М и М0 принадлежат траектории эллипса, следовательно, решение верно.
Направление положительного отсчета по траектории идёт от точки М0 в момент времени t =0 c, к точке М, когда t =1 с (против движения часовой стрелки).
2. Определим скорость точки М в заданный момент времени t.
Известно, что скорость можно разложить по проекциям на координатные оси:

Определим проекцию скорости точки М на ось Ох:

В заданный момент времени t =1 с, проекция скорости составит:

Так, как Vx= -10,9 0, то вектор скорости 

Геометрическая сумма векторов 
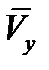
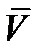
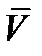
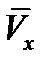
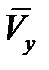

3. Определим ускорение точки М в заданный момент времени t.
Известно, что ускорение можно разложить по проекциям на координатные оси:

Определим проекцию ускорения точки М на ось Ох:

В заданный момент времени t =1с, проекция ускорения составит:

Так, как 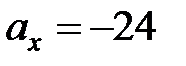
Так, как
Геометрическая сумма векторов 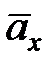
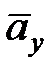

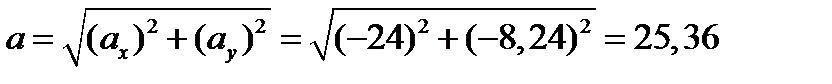
Определим касательное ускорение точки М в заданный момент времени t, зная проекции скорости и ускорения на оси координат:
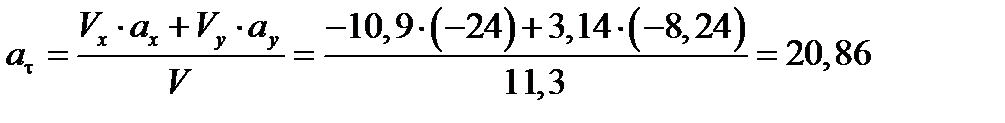
Так, как 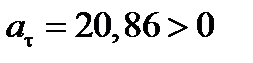

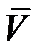
Определим нормальное ускорение точки М в заданный момент времени t, зная полное и касательное ускорения:

Вектор ускорения 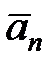
Так, как векторная сумма ускорений 
Определим радиус кривизны траектории 
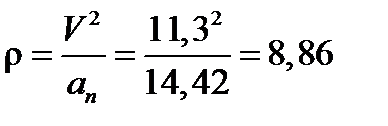
Пример К 1б.Точка движется по дуге окружности радиуса R=2 м по закону 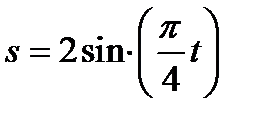
Решение.
Определяем скорость точки:
При t1=1 с, получи 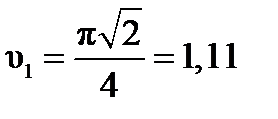
Ускорение находим по его касательной и нормальной составляющим:
Тогда ускорение точки при t1=1 с, будет:
Изобразим на рис. К 1б векторы 
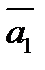
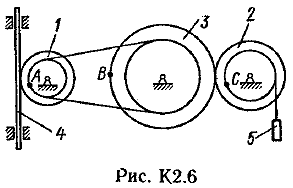
Задача К2.
Механизм состоит из: ступенчатых колес 1–3, находящихся в зацеплении или связанных ременной передачей, зубчатой рейки 4и груза 5, привязанного к концу нити, намотанной на одно из колес (рис. К2.0-К2.9, табл. К2). Радиусы ступеней колес равны соответственно: у колеса 1 – r1=2 см, R1=4см, у колеса 2 – r2=6 см, R2=8см, у колеса 3 – r3=12 см, R3=16 см. На ободьях колес расположены точки А, В и С.
В столбце «Дано» таблицы указан закон движения или закон изменения скорости ведущего звена механизма, где j1(t) – закон вращения колеса 1, s4(t) – закон движения рейки 4, w2(t) – закон изменения угловой скорости колеса 2, υ5(t) –закон изменения скорости груза 5 и т. д. (везде j выражено в радианах, s – в сантиметрах, t – в секундах). Положительное направление для j и w против хода часовой стрелки, для s4, s5 и υ4,υ5 – вниз.
Определить в момент времени t1=2с, указанные в таблице в столбцах «Найти» скорости (υ– линейные, w – угловые) и ускорения (а – линейные, ε – угловые) соответствующих точек или тел (υ5 – скорость груза 5 и т. д.).
 |  |  |
 |  |  |
 |  |  |
 |
Пример К2.
Решение.
1.Определить угловые скорости всех колес как функции времени t. Зная закон движения рейки 1, находим ее скорость:


Тогда, для момента времени t1=3 с, получим w3=6,75 с -1 .
2. Определить ε3. Учитывая второе из равенств (2), 
аАt=36 см/с 2 , аАn=364,5 см/с 2 , 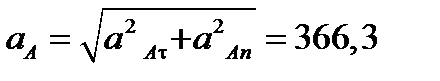
Все скорости и ускорения точек, а также направления угловых скоростей показаны на рис. К2.
Задача К З.
Плоский механизм состоит из стержней 1, 2, 3, 4иползуна В или Е (рис. К З.0-К 3.7) или из стержней 1,2,3и ползунов В и Е (рис. К 3.8, К 3.9), соединенных друг с другом и с неподвижными опорами О1 О2 шарнирами; точка D находится в середине стержня АВ. Длины стержней равны соответственно: l1=0,4 м, l2=1,2 м, l3=1,4м, l4=0,6 м. Положение механизма определяется углами a, β, γ, j, θ. Значения этих углов и других заданных величин, указаны втабл. К 3а (для рис. 0-4) или в табл. К 3б (для рис. 5-9); при этом в табл. К За w1 и w4—величины постоянные.
Определить величины, указанные в таблицах в столбцах «Найти».
Дуговые стрелки, на рисунках, показывают, как при построении чертежа механизма должны откладываться соответствующие углы: по ходу или против хода часовой стрелки(например, угол γ на рис. 8 следует отложить от DB по ходу часовой стрелки, а на рис. 9-против хода часовой стрелки и т. д.).
Построение чертежа начинать со стержня, направление которого определяется углом a; ползун с направляющими для большей наглядности изобразить так, как в примере К 3 (см. рис. К 3б). Заданные, угловую скорость и угловое ускорение, считать направленными против часовой стрелки, а заданные скорость υВ и ускорение аВ от точки В к b (на рис. 5-9).
 |  |  |
 |  |  |
 |  |  |
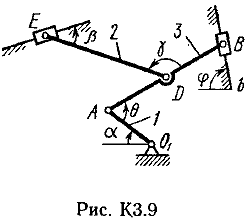 |
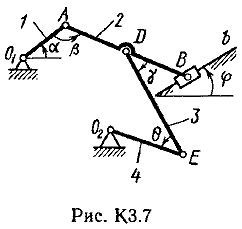
Пример КЗ.

Дано: a=60°, β=150°, γ=90°, j=30°, θ=30°, AD=DB, l1=0,4м, l2=1,2 м, l3=1,4 м, ώ1=2 с -1 , έ=7 с -2 (направления (ώ1 и έ1-против хода часовой стрелки).
Решение.

2. Определяем υB. Точка В принадлежит стержню АВ. Чтобы найти υB, надо знать скорость какой-нибудь другой точки этого стержня и направление υB. По данным задачи, учитывая направление ώ1, можем определить υА, численно:
Направление υВ найдем, учтя, что точка В принадлежит одновременно ползуну, движущемуся вдоль направляющих поступательно. Теперь, зная υА инаправление υB, воспользуемся теоремой о проекциях скоростей двух точек тела (стержня АВ) на прямую, соединяющую эти точки (прямая АВ). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор υB (проекции скоростей должны иметь одинаковые знаки).Затем, вычисляя эти проекции, находим:
3. Определяем υЕ. Точка Е принадлежит стержню DE. Следовательно, по аналогии с предыдущим, чтобы определить υЕ,надо сначала найти скорость точки D, принадлежащей одновременно стержню АВ. Для этого, зная υA и υB, строим мгновенный центр скоростей (МЦС) стержня АВ; это точка С3, лежащая на пересечении перпендикуляров к υА и υB, восставленных из точек А и В (к υА перпендикулярен стержень 1). По направлению вектора υA определяем направление поворота стержня АВ вокруг МЦС С3. Вектор υD перпендикулярен отрезку C3D, соединяющему точки D и С3, и направлен в сторону поворота. Величину υD найдем из пропорции:
Чтобы вычислить С3D и С3В, заметим, что ∆AС3В-прямоугольный, так как острые углы в нем равны 30° и 60°, и что С3В=АB×sin30°=0,5АВ=BD. Тогда ∆ВС3D является равносторонним и С3В=C3D. В результате равенство дает:
Так как точка Е принадлежит одновременно стержню О2Е, вращающемуся вокруг О2, то υЕ ^ О2E. Тогда, расставляя из точек Е и D перпендикуляры к скоростям υЕ иυD,построим МЦС С2стержня DE. По направлению вектора υD определяем направление поворота стержня DE вокруг центра С2. Вектор υE направлен в сторону поворота этого стержня. Из рис. К 3б видно, что ÐC2ED=ÐC2DE=30°, откуда С2Е=C2D. Составив теперь пропорцию, найдем, что:
4. Определяем ώ2. Так, как МЦС стержня 2известен (точка С2)и
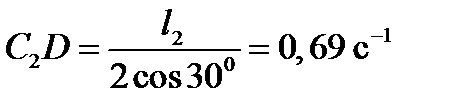

Вектор аА n направлен вдоль АО1,а аА t -перпендикулярно АО1изображаем эти векторы на чертеже (см. рис. К 3в). Так, как точка В одновременно принадлежит ползуну, то вектор аB параллелен направляющим ползуна. Изображаем вектор аB на чертеже, полагая, что он направлен в ту же сторону, что и υB.
Для определения аB воспользуемся равенством:
Изображаем на чертеже векторы а n ВА (вдоль ВА от B к A) и аВА t (в любую сторону перпендикулярно ВА); численно а n B=ώ 2 3l. Найдя ώ3 с помощью построенного МЦС С3 стержня 3, получим:
Таким образом, у величин, входящих в равенство (8), неизвестны только числовые значения аВ и а t ВА,их можно найти, спроектировав обе части равенства (8) на какие-нибудь две оси.
Чтобы определить аВ, спроектируем обе части равенства (8) на направление ВА (ось х),перпендикулярное неизвестному вектору а t ВА. Тогда получим:
Подставив в равенство (10) числовые значения всех величин из (7) и (9), найдем, что:
Так, как получилось aВ>0, то, следовательно, вектор аВ направлен, как показано на рис. К Зв.
6. Определяем έ3. Чтобы найти έ3, сначала определим а t ВА. Для этого обе части равенства (8) спроектируем на направление, перпендикулярное АВ (ось у). Тогда получим:
Подставив в равенство (12) числовые значения всех величин из (11) и (7), найдем, что а t ВА=-3,58 м/с 2 . Знак указывает, что направление а t ВА противоположно показанному на рис. К 3в.
Задача К4
Прямоугольная пластина (рис. К 4.0-К 4.4) или круглая пластина радиуса R=60 см (рис. К 4.5-К 4.9) вращается вокруг неподвижной оси по закону j=f1(t) заданному в табл. К 4. Положительное направление отсчета угла j показано на рисунках дуговой стрелкой. На рис. 0, 1, 2, 5, 6 ось вращения перпендикулярна плоскости пластины и проходит через точку О (пластина вращается в своей плоскости); на рис. 3, 4, 7, 8, 9 ось вращения ОО1лежит в плоскости пластины (пластина вращается в пространстве).
По пластине вдоль прямой BD (рис. 0-4) или по окружности радиуса R (рис. 5-9) движется точка М; закон ее относительного движения, т. е. зависимость s=AM=f2(t)(s-в сантиметрах, t-в секундах), задан в таблице отдельно для рис. 0-4 и для рис. 5-9; там же даны размеры b и l. На рисунках точка М показана в положении, при котором s=AM>0 (при s 2 –0,5t 3 , s=πRcos(πt/3) (j – в радианах, s – в метрах, t – в секундах).
Решение.Рассмотрим движение точки В как сложное, считая ее движение по дуге окружности относительным, а вращение пластины переносным движением. Тогда абсолютная скорость Vабс и абсолютное ускорение аабс точки найдутся по формулам:







где, в свою очередь, 



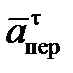
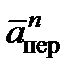
Определим все, входящие в равенства, величины. Рассмотрим каждое движение в отдельности.
1. Относительное движение (мысленно остановить вращение пластины вокруг опоры О). Это движение происходит по закону 
Положение точки В на дуге окружности в момент времени t1=2 с:

Знак минус свидетельствует о том, что точка В в момент t1=2 с находится справа от точки А. Изображаем ее на рис. К4а в этом положении (точка B1).
Тогда 
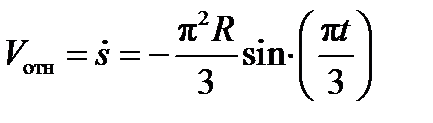

где ρ – радиус кривизны относительной траектории, равный радиусу окружности R. Для момента t1=2 с, учитывая, что R=0,5 м, получим:

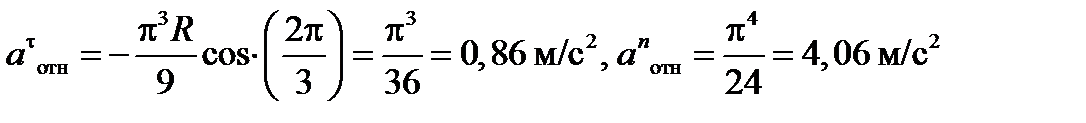
Знаки показывают, что вектор а t отн направлен в сторону положительного отсчета расстояния s, а вектор Vотн-в противоположную сторону; вектор а n отн направлен к центру С окружности. Изображаем все эти векторы на рис. К4а.
2. Переносное движение (мысленно остановить движение точки по окружности). Это движение (вращение) происходит по закону j=t 2 – 0,5t 3 . Найдем угловую скорость w и угловое ускорение ε переносного вращения при t1=2 с:
Знаки указывают, что в момент t1=2 с направления w и ε противоположны направлению положительного отсчета угла j; отметим это на рис. К4а.
Для определения Vпер и апер находим сначала расстояние h1=ОВ1 точки B1 от оси вращения О. Из рисунка видно, что 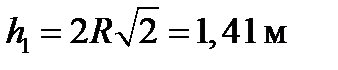


Изображаем на рис. К4а векторы Vпер и a t перс учетом направлений w и εи вектор а n пер (направлен к оси вращения).
3. Ускорение Кориолиса. Модуль ускорения Кориолиса определяем по формуле:
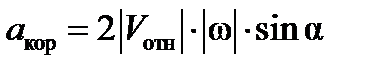
где a – угол между вектором Vотн и осью вращения (вектором w). В нашем случае этот угол равен 90°, так как ось вращения перпендикулярна плоскости пластины, в которой расположен вектор Vотн. Тогда в момент времени t1=2 с, учитывая, что в этот момент |Vотн|=1,42 м/с и |w|=2 с -1 , получим
Направление акорнайдем по правилу Н. Е. Жуковского: так как вектор υотнлежит в плоскости, перпендикулярной оси вращения, то повернем его на 90 0 в направлении ώ, т. е. по ходу часовой стрелки. Изображаем акор на рис. К4а. [Иначе направление акор можно найти, учтя, что акор=2(ώ*υотн)].
Таким образом, значения всех входящих в правые части равенств (1) векторов найдены и для определения υабс и аабс остается только сложить эти векторы. Произведем это сложение аналитически.
4. Определение υа6с. Проведем координатные оси B1xy (см. рис. К4а) и спроектируем почленно обе части равенства
После этого находим
Учитывая, что в данном случае угол между υотн и υперравен 45°, значение υабсможно еще определить по формуле
5. Определение аабс.По теореме о сложении ускорений
Для определения аабс спроектируем обе части равенства (7) на проведенные оси B1xy. Получим
Подставив сюда значения, которые все величины имеют в момент времени t1=2 с, найдем, что в этот момент
Пример К4б.
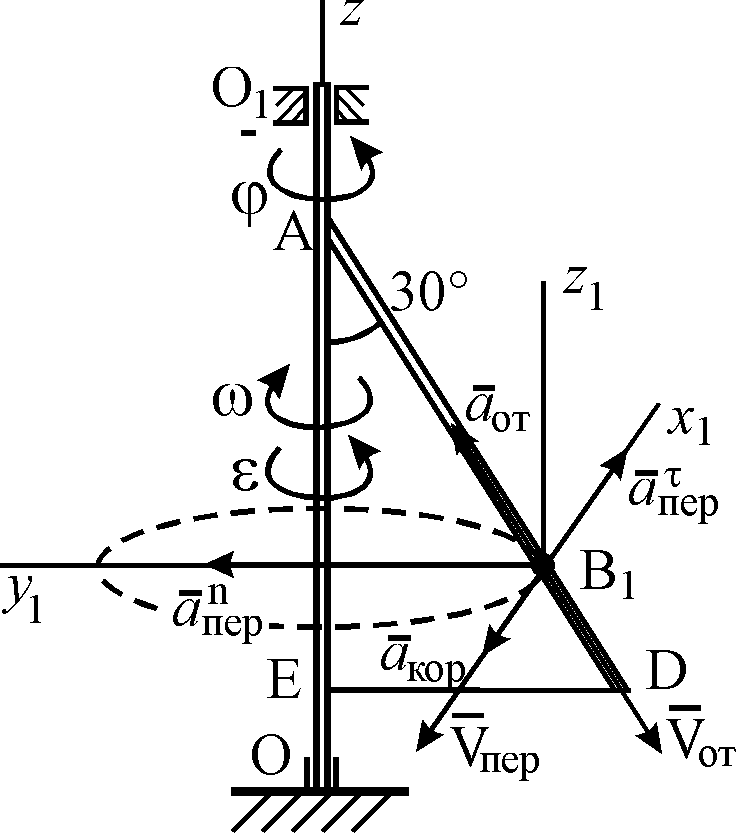
Дано: j = 0,1× t 3 –2,2× t, s = АВ = 2 + 15× t – 3×t 2 ; (j – в радианах, s – в сантиметрах, t – в секундах). Определить: Vабс и аабс в момент времени t1 = 2 с.
| Рис. К4б |
Решение. Рассмотрим движение точки В, как сложное, считая ее движение по прямой AD относительным, а вращение пластины – переносным. Тогда абсолютная скорость 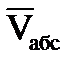
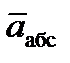
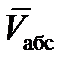
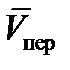

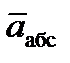



где, в свою очередь, 

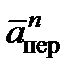
Определим все входящие в равенство величины.
1. Относительное движение — это движение прямолинейное и происходит по закону
В момент времени t1 = 2 с имеем
Знаки показывают, что вектор 

2. Переносное движение. Это движение (вращение) происходит по закону
Найдем угловую скорость w и угловое ускорение e переносного вращения:
w = 

w = — 1 c -1 , e = 1,2 c -2 .
Знаки указывают, что в момент t1 = 2 с направление e совпадает с направлением положительного отсчета угла j, а направление w ему противоположно; отметим это на рис. К3б соответствующими дуговыми стрелками.
Из рисунка находим расстояние h1 точки В1 от оси вращения z:
h1 = AB1× sin 30° = 10 см. Тогда в момент t1 = 2 с, учитывая равенства (68), получаем:


Изобразим на рис. К4б векторы 
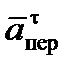
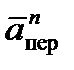

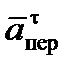
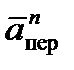
3. Кориолисово ускорение. Так как угол между вектором 

Направление 

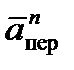


4. Определение Vабс. Так как 
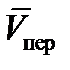



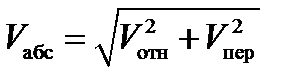
5. Определение аабс. По теореме о сложении ускорений
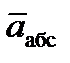


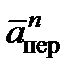

Для определения аабс проведем координатные оси В1хуz1 и вычислим проекции 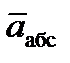


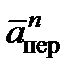

аабс х = | 
аабс у = 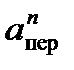
Отсюда находим значение аабс:

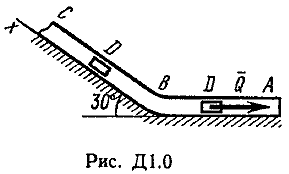
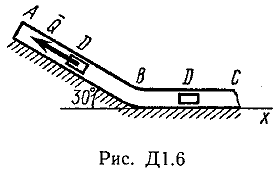
Задача Д1.
Груз D массой m, получив в точке А начальную скорость V0.движется в изогнутой трубе АВС, расположенной в вертикальной плоскости; участки трубы или оба наклонные, или один горизонтальный, а другой наклонный (рис. Д1.0 —Д1.9, табл. Д1).
На участке АВ на груз кроме силы тяжести действуют постоянная сила Q (ее направление показано на рисунках) и сила сопротивления cреды R. зависящая от скорости V груза (направлена против движения); трением груза о трубу на участке АВ пренебречь.
В точке В груз, не изменяя своей скорости, переходит на участок ВС трубы, где на него кроме силы тяжести действуют сила трения
(коэффициент трения груза о трубу f = 0,2) и переменная сила F, проекция которой Fx на ось х задана в таблице.
Считая груз материальной точкой и зная расстояние АВ=l или
время t движения груза от точки А до точки В, найти закон движения груза на участке ВС, т. е. х = x(t). где х = ВD.
Указания.
Задача Д1 — на составление и интегрирование дифференциальных уравнений движения точки (решение основной задачи динамики). Решение задачи разбивается на две части. Сначала нужно составить векторное уравнение движения точки (груза) на участке АВ, спроектировать это уравнение на координатную ось, направленную вдоль АВ, и проинтегрировать полученное дифференциальное уравнение методом разделения переменных, учитывая начальные условия (вторая задача динамики точки). Затем, зная время движения груза на участке АВ или длину этого участка, определить скорость груза в точке В. Эта скорость будет начальной для движения груза на участке ВС.
Посте этого нужно составить векторное уравнение движения точки на участке ВС и спроектировать это уравнение на 2 координатные оси, направленные вдоль ВС и перпендикулярно ВС. Затем проинтегрировать дифференциальное уравнение движения груза на участке ВС тоже с учетом начальных условий, ведя отсчет времени от момента, когда груз находится в точке В, и полагая в этот момент t = 0. При интегрировании уравнения движения на участке АВ в случае, когда задана длина l участка, целесообразно перейти в уравнении от переменных Vx , t к переменным Vх, x, учитывая, что
Груз D массой m, получив в точке А начальную скорость υ0, движется в изогнутой трубе ABC, расположенной в вертикальной плоскости; участки трубы или оба наклонные, или один горизонтальный, а другой наклонный (рис. Д1.0-Д1.9, табл. Д1).
На участке АВ на груз кроме силы тяжести действуют постоянная сила Q (ее направление показано на рисунках) и сила сопротивления среды R, зависящая от скорости υ груза (направлена против движения) ; трением груза о трубу на участке АВ пренебречь.
В точке В груз, не изменяя своей скорости, переходит на участок ВС трубы, где на него кроме силы тяжести действуют сила трения (коэффициент трения груза о трубу f=0,2) и переменная сила F, проекция которой Fx на ось х задана в таблице.
Считая груз материальной точкой и зная расстояние АВ=l или время t1 движения груза от точки А до точки В, найти закон движения груза на участке ВС, т. е. х=f(t), где х=BD.
 | 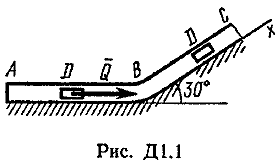 | 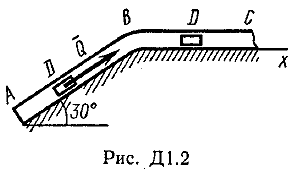 |
 | 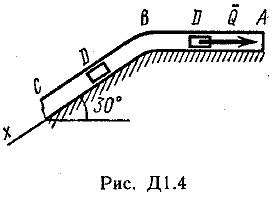 | 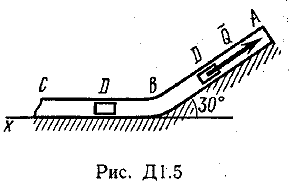 |
 |  |  |
 |
Пример Д1.

Определить: х=f(t)-закон движения груза на участке ВС.
Решение.1.Рассмотрим движение груза на участке АВ, считая груз материальной точкой. Изображаем груз (в произвольном положении) и действующие на него силы Р=mg и R. Проводим ось Аz и составляем дифференциальное уравнение движения груза в проекции на эту ось:
Далее находим Рz=Р=mg, Rz=-R=-mυ 2 , подчеркиваем, что в уравнении все переменные силы надо обязательно выразить через величины, от которых они зависят.Учтя еще, что υz=υ, получим
Введем для сокращения записей обозначения
где при подсчете принято g=10 м/с 2 . Тогда уравнение (2) можно представить в виде
Разделяя в уравнении (4) переменные, а затем беря от обеих частей интегралы, получим
В результате находим
Полагая в равенстве (6) z=l= 2,5 м и заменяя k и п их значениями (3), определим скорость υB груза в точке В (υо=5 м/с, число е=2,7):
2. Рассмотрим теперь движение груза на участке ВС; найденная скорость υВ будет для движения на этом участке начальной скоростью (υ0=υВ). Изображаем груз (в произвольном положении) и действующие на него силы Р=mg,N,Fтр и F. Проведем из точки В оси Вх и By и составим дифференциальное уравнение движения груза в проекции на ось Вх:
где Fтp=f×N. Для определения N составим уравнение в проекции на ось By. Так как ау=0, получим 0=N-mg×cosa, откуда N=mg×cosa. Следовательно, Fтр=fmg×cosa; кроме того, Fx=16sin(4t) и уравнение (8) примет вид
Разделив обе части равенства на т, вычислим g(sina-f×cosa)=g(sin30°-0,2cos30°)=3,2; 
Умножая обе части уравнения (10) на dt и интегрируя, найдем
Будем теперь отсчитывать время от момента, когда груз находится в точке В, считая в этот момент t=0. Тогда при t=0 υ=υ0=υB, где υB даётся равенством (7). Подставляя эти величины в (11), получим
При найденном значении С2 уравнение (11) дает
Умножая здесь обе части на dt и снова интегрируя, найдем
Так как при t=0 х=0, то С3=0 и окончательно искомый закон движения груза будет
где х-в метрах, t-в секундах.
Задача Д2.
Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3с радиусами ступеней R3=0,3 м, r3=0,1 м и радиусом инерции относительно оси вращения ρ3=0,2 м, блока 4радиуса R4=0,2 м и катка (илиподвижного блока) 5 (рис. Д6.0-Д6.9, табл. Д6); тело 5считать сплошным однородным цилиндром, а массу блока 4—равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f=0,1.Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3(или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с.
Под действием силы F=f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сил сопротивления (от трения в подшипниках).
Определить значение искомой величины в тот момент времени, когда перемещение s станет равным s1=0,2 м. Искомая величина указана в столбце «Найти» таблицы, где обозначено: υ1, υ2, υC5—скорости грузов 1, 2 ицентра масс тела 5 соответственно, ώ3 и ώ4-угловые скорости тел 3и 4.
Все катки, включая и катки, обмотанные нитями (как, например, каток 5на рис. 2), катятся по плоскостям без скольжения.
На всех рисунках не изображать груз 2, если т2=0; остальные тела должны изо
Видео:Траектория и уравнения движения точки. Задача 1Скачать

Определение уравнения траектории точки
Страницы работы
Содержание работы
Задание для контрольной работы по теоретической механике (кинематика К1)
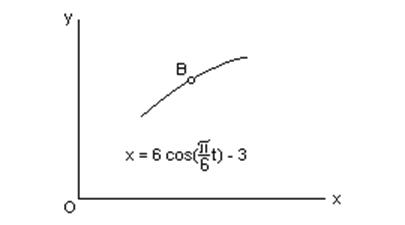
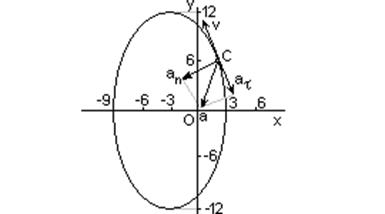
Точка В движется в плоскости xy(траектория точки показана на рисунке условно). Закон движения точки задан уравнениями x = f1(t) (приведен на рисунке) и y=12sin(pt/6), где x и y выражены в сантиметрах, t – в секундах. Найти уравнение траектории точки, для момента времени t = 1с определить скорость и ускорение точки, а также касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
Для определения уравнения траектории точки исключим из заданных уравнений движения время t:
Отсюда 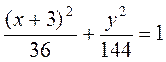
Скорость точки найдем по ее проекциям на координатные оси:
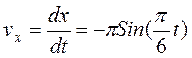
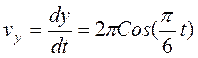
и при t=1c vx=-1.57 см/с, vy=5.44 см/с, v=5.662 см/с (вектор скорости направлен по касательной к траектории).
Аналогично найдем ускорение точки:
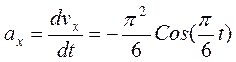
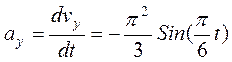
и при t=1c ax=-1.423 см/с 2 , ay=-1.643 см/с 2 , a=2.174 см/с 2 .
Касательное ускорение найдем, дифференцируя по времени равенство v 2 =vx 2 +vy 2 . Получим
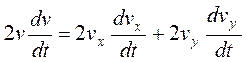
Подставляя сюда численные значения всех величин, найденные нами, найдем, что при t=1c at= -1.197 см/с 2 (поскольку касательное ускорение отрицательное, направляем его противоположно вектору скорости).
Нормальное ускорение точки 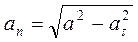
Радиус кривизны траектории r=v 2 /an. Подставляя сюда числовые значения v и an получим, что при t=1с r=17.66 см.
🔥 Видео
ЕГЭ по математике. Профильный уровень. Задание 7. Закон движения. ПроизводнаяСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Кинематика. Закон движения. Урок 3Скачать

К1 Определение скорости и ускорения точки по заданным уравнениям ее движенияСкачать

Кинематика точки в плоскости. ТермехСкачать

Движение точки тела. Способы описания движения | Физика 10 класс #2 | ИнфоурокСкачать

кинематика точкиСкачать

РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ физика 9 ПерышкинСкачать

Естественный способ задания движенияСкачать

Материальная точка движется вдоль оси OX по законуСкачать

Определение реакций опор простой рамыСкачать

Кинематика точки. Три способа задания движения. Скорость, ускорениеСкачать

Задача на движение материальной точки - bezbotvyСкачать

Математика без Ху!ни. Непрерывность функции, точки разрыва.Скачать

Урок 7. Механическое движение. Основные определения кинематики.Скачать

Математика без Ху!ни. Нахождение асимптот, построение графика функции.Скачать

Урок 18 (осн). Координаты тела. График движения. График скоростиСкачать

ФИЗИКА 10 класс : Механическое движение | Материальная точка, траектория, перемещение.Скачать