Точка участвует одновременно в двух взаимно перпендикулярных колебаниях уравнения которых

Видео:Сложение взаимно перпендикулярных гармонических колебанийСкачать

Точка участвует одновременно в двух взаимно перпендикулярных колебаниях уравнения которых

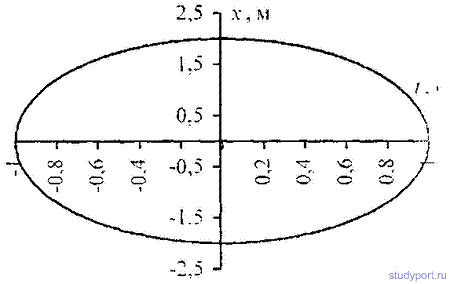
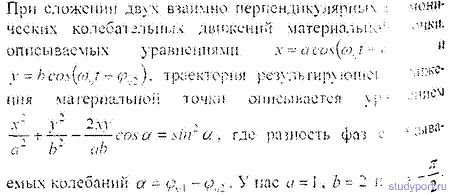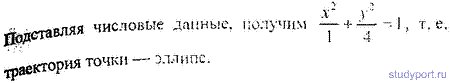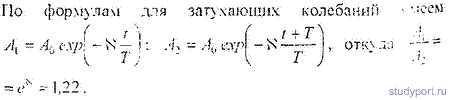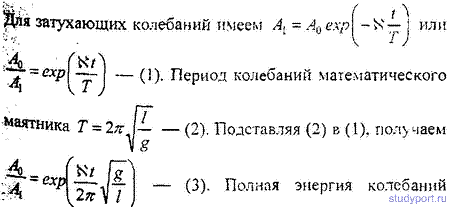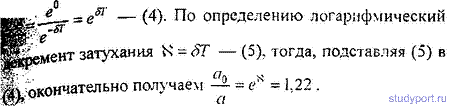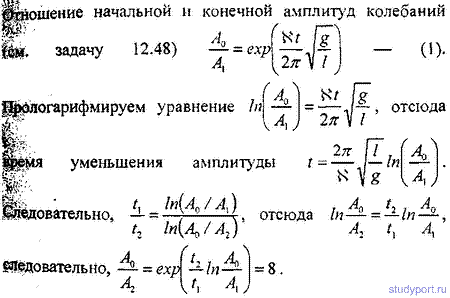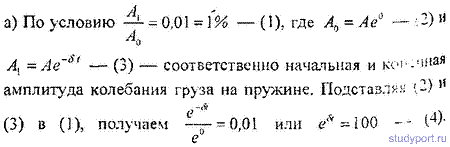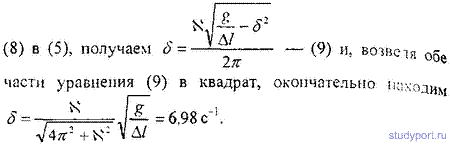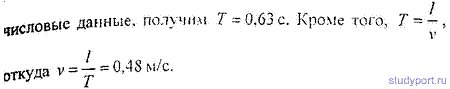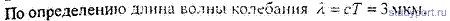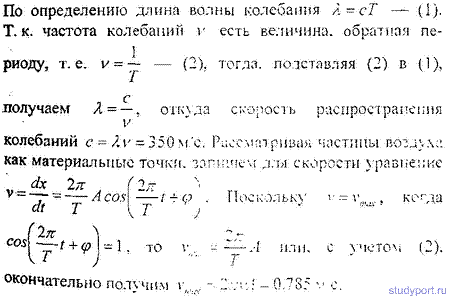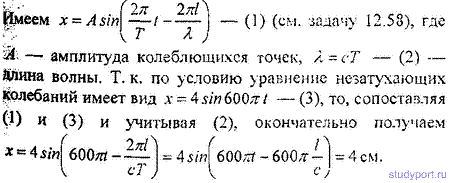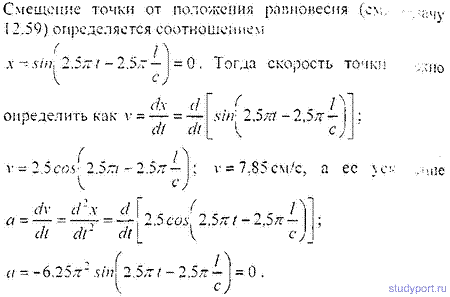Гармоническое колебательное движение и волны

Точка участвует в двух взаимно перпендикулярных колебаниях х = 2 sin ωt м и y = 2 cos ωt м. Найти траекторию результирующего движения точки.

Дано:

Решение:

Уравненние данные в условии запишем в виде

При сложении двух взаимно перпендикулярных колебаний с разностью фаз равной , результирующее колебание происходит по эллипсу, а при

равенстве амплитуд складываемых колебаний по окружности с радиусом равным амплитуде складываемого колебания. Уравнение

Видео:67. Сложение колебанийСкачать

Точка одновременно участвует в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями: x = sinпt (мм) и y = cosп(t + 0,5) (мм). Найти уравнение траектории точки y(x). Изобразить траекторию.

Готовое решение: Заказ №8366

Тип работы: Задача

Статус: Выполнен (Зачтена преподавателем ВУЗа)

Предмет: Физика

Дата выполнения: 21.08.2020

Цена: 227 руб.

Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.

Кстати, если эта работа не по вашей теме или не по вашим данным , не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу , я смогу выполнить её в срок 1-3 дня!

Описание и исходные данные задания, 50% решения + фотография:

№1 314. Точка одновременно участвует в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями: x = sinпt (мм) и y = cosп(t + 0,5) (мм). Найти уравнение траектории точки y(x). Изобразить траекторию.

Преобразуем выражение для координаты у: . То есть: . Это и есть уравнение траектории точки. Поскольку синус принимает значения от -1 до 1, то точка будет двигаться по отрезку прямой от точки (0; 0) к точке А(1; -1); затем в обратную сторону к точке В(-1; 1); затем снова к точке А и т. д. Изобразим траекторию точки.

• Складываются два взаимно перпендикулярных колебания, выражаемых уравнениями x = 2 sin пt, y = cos п(t + 0,5) (длина в сантиметрах, время в секундах). Найти уравнение траектории и построить её на чертеже, показав направление движения точки.
• Точка совершает одновременно два гармонических колебания, происходящих по взаимно перпендикулярным направлениям и выражаемым уравнениями: x = A1 cos w1t и y = A2 cos w2(t + t), где A1 = 4 см, w1 = п с-1, A2 = 8 см, w2 = п с-1, t = 1 с. Найти уравнение траектории и начертить её с соблюдением масштаба.
• Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, уравнения которых x = A1sinw1t и y = A2cosw2t, где A1 = 8 см, A2 = 4 см, w1 = w2 = 4 с-1. Написать уравнение траектории и построить её. Показать направление движения точки.
• Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями x = A coswt, y = B coswt, где A = 2 см, B = 3 см. Найти уравнение траектории точки и построить траекторию с соблюдением масштаба. Указать направление движения точки и пояснить свой ответ.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Урок 342. Сложение взаимно перпендикулярных колебаний. Фигуры ЛиссажуСкачать

Гармоническое колебательное движение и волны

12.41. Точка участвует в двух взаимно перпендикулярных колебаниях x = sinPt и y = 2sin(Pt+P/2). Найти траекторию результирующего движения точки.

12 42. Точка участвует в двух взаимно перпендикулярных колебаниях х = sinPt a y = 4sin(Pt + P). Найти траекторию результирующего движения точки и начертить ее с нанесением масштаба.

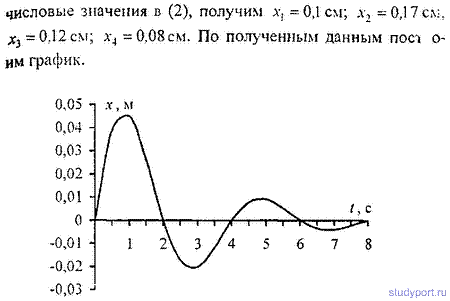
12.43. Период затухающих колебаний T = 4с; логарифмический декремент затухания N = 1.6; начальная фаза φ = 0. При t=T/4 смещение точки x = 4,5 см. Написать уравнение движения

этого колебания. Построить график этого колебания в пределах двух периодов.

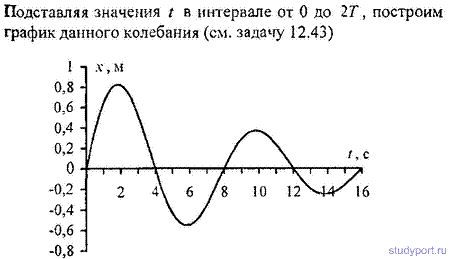
12.44. Построить график затухающего колебания, данного

уравнением x=5e -0,1t sinP/4t м.

12.45. Уравнение затухающих колебаний дано в виде x=5e -0,25t sinP/2tм. Найти скорость v колеблющейся точки в моменты времени t, равные: 0, T, 2T, 3Т и 4T,

12.46. Логарифмический декремент затухания математического маятника N = 0.2. Во сколько раз уменьшится амплитуда колебаний за одно полное колебание маятника?

12.47. Найти логарифмический декремент затухания математического маятника, если за время t = 1мин амплитуда колебаний уменьшилась в 2 раза. Длина маятника l= 1м.

12.48. Математический маятник длиной l = 24,7 см совершает затухающие колебания. Через какое время t энергия колебаний маятника уменьшится в 9,4 раза? Задачу решить при значении логарифмического декремента затухания: а) N = 0,01; б) N = 1.

12.49. Математический маятник совершает затухающие колебания с логарифмическим декрементом затухания N = 0,2 . Во сколько раз уменьшится полное ускорение маятника в его крайнем положении за одно колебание?

12.50. Амплитуда затухающих колебаний математического маятника за время t = 1 мин уменьшилась вдвое. Во сколько раз уменьшится амплитуда за время t = 3 мин?

12.51. Математический маятник длиной l = 0,5м, выведенный из положения равновесия, отклонился при первом колебании на х₁ = 5 см, а при втором ( в ту же сторону) — на x₂ = 4см. Найти время релаксации t, т. е. время, в течение которого амплитуда колебаний уменьшится в е раз, где е — основание натуральных логарифмов.

12.52. К вертикально висящей пружине подвешивают груз. При этом пружина удлиняется на dl = 9,8см. Оттягивая этот груз вниз и отпуская его, заставляют груз совершать колебания. Каким должен быть коэффициент затухания δ, чтобы: а) колебания прекратились через время t = 10 с (считать условно, что колебания прекратились, если их амплитуда упала до 1% от начальной); б) груз возвращается в положение равновесия апериодически; в) логарифмический декремент затухания колебаний был равным N = 6 ?

12.53. Тело массой m = 10 г совершает затухающие колебания с максимальной амплитудой A_max = 7см, начальной фазой φ = о и коэффициентом затухания δ = 1,6 см -1 . На это тело начала действовать внешняя периодическая сила F, под действием которой установились вынужденные колебания. Уравнение вынужденных колебаний имеет вид х = 5sin(10Pt-3P/4) см. Найти (с числовыми коэффициентами) уравнение собственных колебаний и уравнение внешней периодической силы.

12.54. Гиря массой m = 0,2 кг, висящая на вертикальной пружине, совершает затухающие колебания с коэффициентом затухания δ= 0,75 см -1 . Жесткость пружины k = 0,5кН/м. Начертить зависимость амплитуды А вынужденных колебаний гирьки от частоты внешней периодической силы, если известно, что максимальное значение внешней силы F₀ = 0,98 Н. Для построения .трафика найти значение А для частот: w= 0, w= 0,5, w = 0,75, w = w₀, w = w=1,5w₀ и w = 2w₀, где w₀— частота собственных колебаний подвешенной гири.

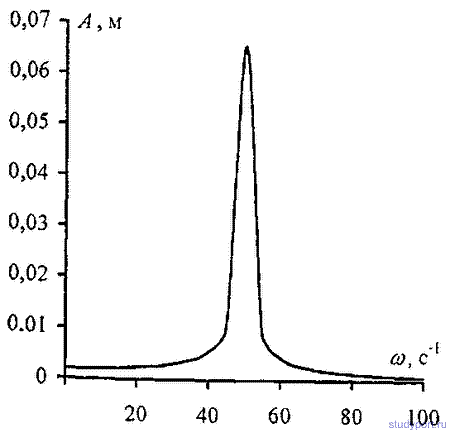
12.55. По грунтовой дороге прошел трактор, оставив следы в виде ряда углублений, находящихся на расстоянии l = 30 см друг от друга. По этой дороге покатили детскую коляску, имеющую две одинаковые рессоры, каждая из которых прогибается на x₀ = 2 см под действием груза массой m₀ = 1 кг. С какой скоростью v катили коляску, если от толчков на углублениях она, попав в резонанс, начала сильно раскачиваться? Масса коляски M= 10 кг.

12.56. Найти длину волны λ колебания, период которого T = 10 -14 с. Скорость распространения колебаний с = 3 * 10 8 м с.

12.57. Звуковые колебания, имеющие частоту v = 500 Гц и амплитуду A =0.25 мм. распространяются в воздухе. Длина волны λ = 70 см. Найти скорость с распространения колебаний и максимальную скорость V_max частиц воздуха.

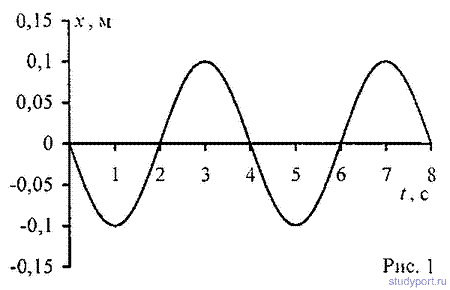
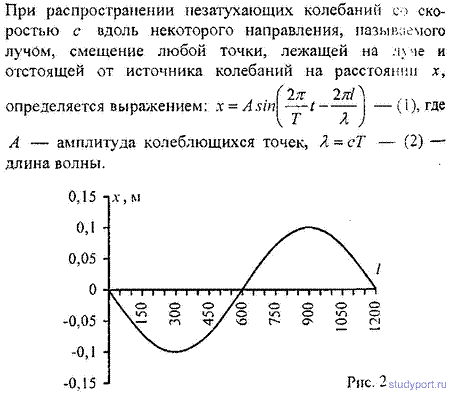
12.58. Уравнение незатухающих колебаний имеет вид

x=10sinP/2*t см. Найти уравнение волны, если скорость распространения колебаний с = 300м*с. Написать и изобразить графически уравнение колебания для точки, отстоящей на расстоянии

l = 600 м от источника колебаний. Написать и изобразить графически уравнение колебания для точек волны в момент времени t= 4 с после начала колебаний.

12.59. Уравнение незатухающих колебаний имеет вид x = 4sin600Pt см. Найти смещение x от положения равновесия

точки, находящейся на расстоянии l = 75 см от источника колебаний, для момента времени t = 0,01 с после начала колебаний. Скорость распространения колебаний с = 300 м/с.

12.60. Уравнение незатухающих колебаний имеет вид x=sin2,5Pt см. Найти смещение х от положения равновесия, скорость v и ускорение a точки, находящейся на расстоянии

l = 20м от источника колебаний, для момента времени t = 1с после начала колебаний. Скорость распространения колебаний с = 100 м*с.

Ошибка в тексте? Выдели её мышкой и нажми

Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!

Видео:7 класс, 30 урок, Углы с соответственно параллельными или перпендикулярными сторонамиСкачать

ФИЗИКИ помогитеМатериальная точка участвует одновременно в двух взаимно перпендикулярны колебаниях, уравнения которых имеют вид : х = cos2πt и y = 2cosπt?

Физика | 10 — 11 классы

Материальная точка участвует одновременно в двух взаимно перпендикулярны колебаниях, уравнения которых имеют вид : х = cos2πt и y = 2cosπt.

Определить траекторию движения точки и начертить ее с соблюдением масштаба.

Если точка движется по замкнутой кривой, то укажите направление движения.

Если же траектория движения не замкнута, то покажите пределы ее.

Исключим время разделив первое уравнение на второе :

x / y = cospi * t / 2 * cospit = 1 / 2

y = 2 * x Траектория прямая, пределы(0, бесконечность).

Видео:Фигуры ЛиссажуСкачать

Покажите на рисунке траекторию и перемещение при движении маятника из точки В в точку С ; из точки С в точку АПомогите пожалуйста, заранее спасибо?

Покажите на рисунке траекторию и перемещение при движении маятника из точки В в точку С ; из точки С в точку А

Помогите пожалуйста, заранее спасибо!

Видео:Урок 95. Теорема о взаимно перпендикулярных осяхСкачать

Какой может быть траектория материальной точки, если она движется с постоянным по величине и направлению ускорением?

Какой может быть траектория материальной точки, если она движется с постоянным по величине и направлению ускорением?

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Может ли траектория движения иметь точки пересечения?

Может ли траектория движения иметь точки пересечения?

Видео:Урок 343. Затухающие колебания (часть 1)Скачать

88. Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями : х = 0, 01 sin ωt, у = 0, 02 sin (ωt + ?

88. Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями : х = 0, 01 sin ωt, у = 0, 02 sin (ωt + π).

Найти уравнение траектории точки, построить ее с соблюдением масштаба и указать направление движения.

Видео:Урок 337. Сложение колебаний одной частоты. Метод векторных диаграммСкачать

Движение материальной точки в данной системе отсчета описывается уравнениями у = 1 + 2t, х = 2 + t?

Движение материальной точки в данной системе отсчета описывается уравнениями у = 1 + 2t, х = 2 + t.

Найти уравнение траектории.

Построить траекторию на плоскости XOY.

Указать положение точки t = 0, направление и скорость движения.

Если можно то с графиком и с объяснением.

Видео:Лекция 1 КолебанияСкачать

Уравнения движения материальной точки в плоскости XOY имеют вид x = 25t, м, у = 0, 2 + t, м?

Уравнения движения материальной точки в плоскости XOY имеют вид x = 25t, м, у = 0, 2 + t, м.

Определите уравнение траектории материальной точки.

Видео:Колебания и волны. Лекция 2. Энергия гармонических колебаний материальной точкиСкачать

Материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях, происходящих согласно уравнениям : x = А1 cosω1t и y = А2 sinω2t, где А1 = 2 см ; ω1 = 2 с–1 ; А2 = 4 см ; ω2 = 2 ?

Материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях, происходящих согласно уравнениям : x = А1 cosω1t и y = А2 sinω2t, где А1 = 2 см ; ω1 = 2 с–1 ; А2 = 4 см ; ω2 = 2 с–1.

Определите траекторию точки.

Постройте траекторию с соблюдением масштаба, укажите направление движения точки.

Видео:Лекция 2 ВолныСкачать

Материальная точка движется в плоскости XOY?

Материальная точка движется в плоскости XOY.

Уравнение движения имеют вид : x = 3t + 5 и y = 4t — 3.

С какой скоростью движется точка?

Видео:лекция 421 План курса Периферийные устройства.Скачать

Материальная точка движется по плоскости XY?

Материальная точка движется по плоскости XY.

Движение точки даны этими уравнениями x = 3sinwt, y = 2coswt.

Надо определить траекторию точки.

Видео:Материальная точка .Нарисовать траекториюСкачать

Начертите траекторию движения точки обода велосипедного колеса при равномерном и прямолинейном движении велосепидиста относительно спиц в колесе?

Начертите траекторию движения точки обода велосипедного колеса при равномерном и прямолинейном движении велосепидиста относительно спиц в колесе.

Вы находитесь на странице вопроса ФИЗИКИ помогитеМатериальная точка участвует одновременно в двух взаимно перпендикулярны колебаниях, уравнения которых имеют вид : х = cos2πt и y = 2cosπt? из категории Физика. Уровень сложности вопроса рассчитан на учащихся 10 — 11 классов. На странице можно узнать правильный ответ, сверить его со своим вариантом и обсудить возможные версии с другими пользователями сайта посредством обратной связи. Если ответ вызывает сомнения или покажется вам неполным, для проверки найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте новый вопрос, используя ключевые слова: введите вопрос в поисковую строку, нажав кнопку в верхней части страницы.

📽️ Видео

Выполнялка 53.Гармонические колебания.Скачать

1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Сложение колебаний, Киевнаучфильм, 1978Скачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать