точка совершает гармонические колебания
Точка совершает гармонические колебания, уравнение которых имеет вид х = A sin ωt, где A = 5 см; ω = 2 с. В момент, когда на точку действовала возвращающая сила F = +5 мН, точка обладала потенциальной энергией П = 0,1 мДж. Найти этот момент времени t и соответствующую ему фазу φ колебания.
Точка совершает гармонические колебания с периодом T = 6 с и начальной фазой, равной нулю. Определите, за какое время, считая от начала движения, точка сместится от положения равновесия на половину амплитуды.
За какую часть периода точка, совершающая гармонические колебания, пройдет путь, равный 0,828 А, где А — амплитуда колебаний, если в начальный момент точка находилась в положении равновесия?
Точка совершает гармонические колебания с периодом 2 с. Амплитуда колебаний 10 см. Найти смещение, скорость и ускорение точки спустя 0,2 с после ее прохождения через положение равновесия. Начало колебаний связано с положением равновесия.
Точка совершает гармонические колебания с частотой 10 Гц. В момент, принятый за начальный, точка имела максимальное смещение 1 мм. Написать уравнение колебаний точки и начертить их график.
Точка совершает гармонические колебания с начальной фазой, равной нулю. Найдите период колебаний, если известно, что за время, равное 3 с, считая от начала движения, точка сместилась от положения равновесия на 7/10 амплитуды.
Через какое время от начала движения точка, совершающая гармоническое колебание, сместится от положения равновесия на половину амплитуды? Период колебаний m = 24 с, начальная фаза φ = 0.
Точка совершает гармоническое колебание. Период колебаний Т = 2 с, амплитуда А = 50 мм, начальная фаза φ = 0. Найти скорость v точки в момент времени, когда смещение точки от положения равновесия x = 25 мм.
Точка совершает гармонические колебания. Наибольшее смещение xmax точки равно 10 см, наибольшая скорость 

Максимальная скорость 

Точка совершает гармонические колебания по закону x = 3cos(πt/2+π/8), м. Определите: 1) период колебаний, 2) максимальную скорость vmax точки; 3) максимальное ускорение аmаx точки.
Точка совершает гармонические колебания. В некоторый момент времени смещение точки x = 5 см, скорость ее v = 0,2 м/с и ускорение a = –0,8 м/с 2 . Найти циклическую частоту, период колебаний, фазу и амплитуду колебаний в рассматриваемый момент времени.
Точка совершает гармонические колебания согласно уравнению x = 0,4 sinπt (м). Определить скорость и ускорение точки через 1/6 с от начала колебаний.
За какую часть периода точка, совершающая гармонические колебания, пройдет путь, равный 0,829 А, где А — амплитуда колебаний, если в начальный момент точка находилась в положении равновесия?
Точка совершает гармонические колебания вдоль некоторой прямой с периодом Т = 0,60 с и амплитудой а = 10,0 см. Найти среднюю скорость точки за время, в течение которого она проходит путь а/2: а) из крайнего положения; б) из положения равновесия.
Максимальная скорость точки, совершающей гармонические колебания равна υ = 10 см/с, максимальное ускорение а = 100 см/с 2 . Найти угловую частоту ω колебаний, их период T и амплитуду A.
За какую часть периода точка, совершающая гармонические колебания, пройдет путь, равный 0,583А, где А – амплитуда колебаний, если в начальный момент точка находилась в положении равновесия?
- Точка совершает простые гармонические колебания, уравнение которых x = A sinwt, где A = 5 см, w = 2 с-1.
- Описание и исходные данные задания, 50% решения + фотография:
- Примеры решенных задач по физике -Контрольная 1(гармонические колебания, плоские волны, кольца Ньютона, дифракция, поляризация света)
- 📹 Видео
Видео:Гармонические колебания | Физика 9 класс #25 | ИнфоурокСкачать

Точка совершает простые гармонические колебания, уравнение которых x = A sinwt, где A = 5 см, w = 2 с-1.






Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.
Кстати, если эта работа не по вашей теме или не по вашим данным , не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу , я смогу выполнить её в срок 1-3 дня!
Описание и исходные данные задания, 50% решения + фотография:
№2-2 Задача 173. Точка совершает простые гармонические колебания, уравнение которых x = A sinwt, где A = 5 см, w = 2 с-1. В момент времени, когда точка обладала потенциальной энергией П = 0,1 мДж, на неё действовала возвращающая сила F = 5 мН. Найти этот момент времени t.
Смещение точки в произвольный момент времени определяется уравнением: , где – амплитуда колебаний; – круговая частота колебаний. Найдём зависимость скорости точки от времени: . Найдём зависимость ускорения точки от времени: . В момент времени на точку действует возвращающая сила:
| Если вам нужно решить физику, тогда нажмите ➔ заказать контрольную работу по физике. |
| Похожие готовые решения: |
- Колебания материальной точки происходят согласно уравнению x = A coswt, где A = 8 см, w = п/6 с-1. В момент, когда возвращающая сила F в первый раз достигла значения -5 мН, потенциальная энергия П точки стала равной 100 мкДж. Найти этот момент времени t и соответствующую ему фазу Dt.
- Колебания материальной точки происходят согласно уравнению x = A coswt, где A = 8 см, w = п/6 с-1. В момент, когда возвращающая сила в первый раз достигла значения F = – 5 мН, потенциальная энергия точки стала равной Wp = 100 мкДж. Определить этот момент времени t и соответствующую ему фазу ф.
- Точка совершает гармонические колебания, уравнение которых имеет вид x = 0,05 sin2t (длина – в метрах, время – в секундах). Найти момент времени (ближайший к началу отсчета), в который потенциальная энергия точки равна 10-4 Дж, а возвращающая сила равна 5•10-3 Н. Определить фазу колебаний в этот момент времени.
- Точка совершает гармонические колебания согласно уравнению: x = 0,05 sin2t (м). В момент времени, когда потенциальная энергия точки была равна 0,1 мДж, на неё действовала возвращающая сила 5 мН. Найти этот момент времени.
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Примеры решенных задач по физике -Контрольная 1(гармонические колебания, плоские волны, кольца Ньютона, дифракция, поляризация света)
Ниже приведены условия и решения задач. Закачка решений в формате doc начнется автоматически через 10 секунд.
Точка совершает гармонические колебания с амплитудой А=10 см и периодом Т=5 с. О п ределите для точки : 1) максимальную скорость, 2) максимальное ускорение.
Дано : A =10 см=0 .1 м
Найти : v max , a max
Уравнение гармонического колебания точки имеет вид :
x = Acos ( ω t + φ ) (1)
Формулу скорости получим, взяв первую производную по времени от смещения :
v= 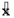
Максимальная скорость точки равна :
v max =- A ω (2) , где А – амплитуда колебаний ; ω – круговая частота колебаний.
Круговая частота колебаний ω связана с периодом колебаний Т выражением :
С учётом (3) формула (2) примет вид :
v max =-2 π A / T (4)
Ускорение точки найдём, взяв производную по времени от скорости :
a= 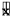
Максимальное ускорение, равно :
С учётом (3) перепишем формулу (5) в виде :
a max =-4 π 2 A / T 2 (6)
Производя вычисления по формулам (4) и (6), найдём максимальные скорость и ускорение точки.
v max =-2×3.14×0.1/5=-0.13 м/с
a max =-4×3.14 2 ×0.1/5 2 =-0.16 м/с 2
Ответ : v max =-0.13 м/с ; a max =-0.16 м/с 2
Волна с периодом Т=1.2 с и амплитудой колебания А=2 см распространяется со скоростью 15 м/с. Чему равно смещение точки, находящейся на расстоянии 45 м от источника волн в тот момент, когда от начала колебаний источника прошло время t = 4 с ?
Уравнение плоской волны имеет вид :
y ( x , t )= Acos ( ω t — kx ) (1) , где y – смещение точек среды с к о ординатой x в момент времени t ; ω – круговая частота ; k – волновое число.
Волновое число k связано с длиной волны λ выражением :
k =2 π / λ (2) , где λ = vT ; v – скорость распространения колебаний ; T – период колебаний.
Циклическая частота ω связана с периодом Т выражением :
С учётом (2) и (3) уравнение (1) примет вид :
y(x,t)=Acos(2 π t/T-2 π x/(vT))=Acos 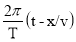
Вычисления по формуле (4), дают :
y (45 ; 4)=0.02× cos 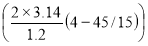
Ответ : y(45 ; 4)=1 см.
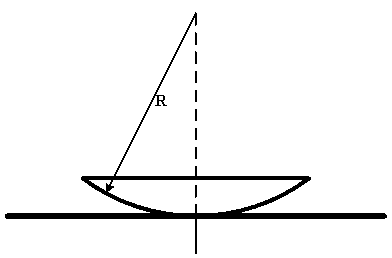
Определить радиус второго темного кольца Ньютона в отраженном свете, если прибор, состоящий из плосковыпуклой линзы с радиусом кривизны 8 м и плоской пластины освещается монохроматическим светом с длиной волны 640 нм.
Дано : λ =64 0 нм= 6.5×10 — 7 м
Радиус темных колец Ньютона в отражённом свете определяется формулой :
r k = 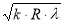
где k – номер кольца ; R – радиус кривизны линзы ; λ – длина волны.
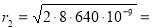
Ответ : r 2 = 3,2∙10 — 3 м .
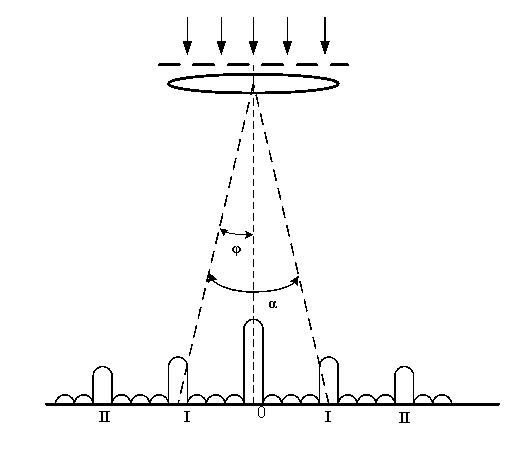
Постоянная дифракционной решётки в n =4 раза больше длины световой волны монохр о ма тического света, нормально падающего на её поверхность. Определить угол α между дв у мя первыми симметричными дифракционными максимумами.
Постоянная дифракционной решётки d , длина волны λ и угол отклонения лучей соо т ветст вующий К – му дифракционному максимуму, связаны соотношением
dsin = kλ , или sin = kλ / d (1)
где к – порядок максимума (в данном случае к=1). Учитывая, что λ/ d =1/ n перепишем форм у лу (1) в виде:
Из рисунка видно, что угол α равен удвоенному углу . Тогда формула (2) примет вид:
sin ( α /2)= k / n , откуда α=2 arcsin ( k / n )
Подставим в последнюю формулу числовые значения и вычислим:
На сколько процентов уменьшается интенсивность света после прохождения через призму Николя, если потери света составляют 10% ?
Естественный свет, падая на грань призмы Николя, расщепляется вследствие двойного л у чепреломления на два пучка : обыкновенный и необыкновенный. Оба пучка одинаковы по интенсивности и полностью поляризованы. Плоскость колебаний необыкновенного пучка лежит в плоскости чертежа. Плоскость колебаний обыкновенного пучка перпенд и кулярна плоскости чертежа. Обыкновенный пучок (о) вследствие полного отражения от грани AB отбрасывается на зачернённую поверхность призмы и поглощается ею. Необы к новенный пучок (е) проходит через призму. При этом интенсивность света уменьшается вследствие поглощения в веществе николя. Таким образом, интенсивность света, пр о шедшего через призму :
где k = 0.1 – относительная потеря интенсивности света в николе ; I 0 – интенсивность е с тественного света, падающего на николь.
Относительное уменьшение интенсивности света получим, разделив интенсивность I 0 ест е ственного света, падающего на первый николь, на интенсивность I 1 поляризованного св е та :
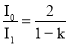
Вычисления по формуле (1) дают :
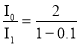
Процентное уменьшение интенсивности :
n % = 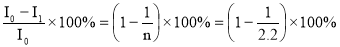
Ответ : при прохождения света через призму интенсивность уменьшится на 54.5%.
Найти длину волны де Бройля для электрона, движущегося по круговой орбите атома водорода, находящегося в основном состоянии.
Длина волны де Бройля λ частицы зависит от её импульса p и определяется формулой :
Импульс частицы можно определить, если известна её скорость v . Связь импульса со скоростью для нерелятивистского (когда v c ) и для релятивистского (когда v ≈ c ) случаев соответственно выражается формулами :
p=m 0 v (2) ; p= 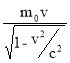
Формула (1) с учётом соотношений (2) и (3) запишется соответственно в нерелятивис т ском и релятивистском случаях :
λ = 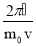
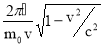
Найдём скорость электрона на круговой орбите атома водорода, находящегося в осно в ном состоянии, из следующих соображений. Согласно теории Бора, радиус r электронной орбиты и скорость v электрона на ней связаны равенством mvr = n ħ . Так как нам требуется скорость электрона на первой орбите, то главное квантовое число n =1 и равенство примет вид :
Откуда скорость электрона :
v = 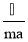
где ħ – постоянная Планка (ħ= 1.05×10 -34 Дж·с) ; m – масса покоя электрона
( m =9.11×10 — 31 кг ) ; a – радиус первой орбиты (а= 5.29×10 — 11 м – Боровский радиус).
Найдём скорость электрона, произведя вычисления по формуле (6) :
v = 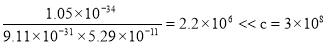
Следовательно , можно применить формулу (4). С учётом (6) формула (4) примет вид :
Вычисления по формуле (7) дают :
λ =2×3.14×5.29×10 -11 =3.3×10 — 10 м
Ответ : λ =3.3×10 — 10 м .=0.33 нм.
Имя файла: physics1.doc
Размер файла: 456.5 Kb
Если закачивание файла не начнется через 10 сек, кликните по этой ссылке
📹 Видео
Урок 327. Гармонические колебанияСкачать

Физика 9 класс. §25 Гармонические колебанияСкачать

5.4 Уравнение гармонических колебанийСкачать

Выполнялка 53.Гармонические колебания.Скачать

Уравнения и графики механических гармонических колебаний. Практ. часть - решение задачи. 11 класс.Скачать

Гармонические колебанияСкачать

Как решить уравнение колебаний? | Олимпиадная физика, механические гармонические колебания, 11 классСкачать

Тема 1. Колебательное движение. Гармонические колебания. Уравнение гармонических колебанийСкачать

Материальная точка совершает гармонические колебанияСкачать

Гармонические колебания | Физика 11 класс #8 | ИнфоурокСкачать

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Небольшой груз, подвешенный на длинной нити, совершает гармонические колебания, при которых - №30970Скачать

10 класс, 19 урок, График гармонического колебанияСкачать

Физика. 11 класс. Уравнение и графика гармонических колебаний /03.09.2020/Скачать

Урок 329. Задачи на гармонические колебания - 1Скачать

Урок 335. Анализ графика гармонических колебанийСкачать

Физика 10 класс. Гармонические колебания. Решение задачСкачать

Физика 9 класс (Урок№11 - Гармонические колебания. Затухающие колебания. Резонанс.)Скачать