Предлагаю вам воспользоваться онлайн калькулятором для вычисления координат точки пересечения прямых.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление координат точки пересечения двух прямых и закрепить пройденный материал.
- Найти точку пересечения прямых
- Ввод данных в калькулятор для вычисления координат точки пересечения прямых
- Дополнительные возможности калькулятора вычисления координат точки пересечения прямых
- Теория. Координаты точки пересечения двух прямых
- Точка пересечения прямых на плоскости онлайн
- Предупреждение
- Точка пересечения прямых на плоскости − теория, примеры и решения
- 1. Точка пересечения прямых, заданных в общем виде.
- 2. Точка пересечения прямых, заданных в каноническом виде.
- 3. Точка пересечения прямых, заданных в параметрическом виде.
- 4. Точка пересечения прямых, заданных в разных видах.
- 5. Примеры нахождения точки пересечения прямых на плоскости.
- Пересечение с осями онлайн
- Другие полезные разделы:
- Оставить свой комментарий:
- 🌟 Видео
Видео:№976. Найдите координаты точки пересечения прямых 4x + 3y-6 = 0 и 2х+у-4 = 0.Скачать
Найти точку пересечения прямых
Уравнение 1-ой прямой:
Уравнение 2-ой прямой:
Ввод данных в калькулятор для вычисления координат точки пересечения прямых
В онлайн калькулятор можно вводить числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора вычисления координат точки пересечения прямых
- Используйте кнопки и на клавиатуре, для перемещения между полями калькулятора.
Теория. Координаты точки пересечения двух прямых
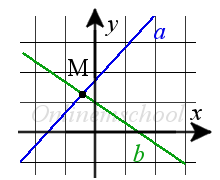
Если точка M, является точкой пересечения двух прямых, то она должна принадлежать этим прямым, а ее координаты удовлетворять уравнения этих прямых.
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:Найти точку пересечения прямой и плоскостиСкачать
Точка пересечения прямых на плоскости онлайн
С помощю этого онлайн калькулятора можно найти точку пересечения прямых на плоскости. Дается подробное решение с пояснениями. Для нахождения координат точки пересечения прямых задайте вид уравнения прямых («канонический», «параметрический» или «общий»), введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать
Точка пересечения прямых на плоскости − теория, примеры и решения
- Содержание
- 1. Точка пересечения прямых, заданных в общем виде.
- 2. Точка пересечения прямых, заданных в каноническом виде.
- 3. Точка пересечения прямых, заданных в параметрическом виде.
- 4. Точка пересечения прямых, заданных в разных видах.
- 5. Примеры нахождения точки пересечения прямых на плоскости.
1. Точка пересечения прямых, заданных в общем виде.
Пусть задана декартова прямоугольная система координат Oxy и пусть в этой системе координат заданы прямые L1 и L2:
| L1: A1x+B1y+C1=0, | (1) |
| L2: A2x+B2y+C2=0 | (2) |
Для нахождения точки пересечения прямых (1) и (2) нужно решить систему линейных уравнений (1) и (2) относительно переменных x,y. Для этого запишем систему (1),(2) в матричном виде:
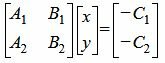 | (3) |
Построим расширенную матрицу:
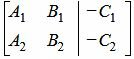 | (4) |
Приведем (4) к верхнему диагональному виду. Пусть A1≠0 . Тогда сложим строку 2 со строкой 1, умноженной на −A2/A1:
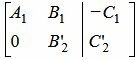 | (5) |
 |
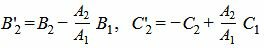Если B’2=0 и С’2=0, то система линейных уравнений имеет множество решений. Следовательно прямые L1 и L2 совпадают. Если B’2=0 и С’2≠0, то система несовместна и, следовательно прямые параллельны и не имеют общей точки. Если же B’2≠0, то система линейных уравнений имеет единственное решение. Из второго уравнения находим y: y=С’2/B’2 и подставляя полученное значение в первое уравнение находим x: x=(−С1−B1y)/A1. Получили точку пересечения прямых L1 и L2: M(x, y).
Подробнее о решении систем линейных уравнений посмотрите на странице метод Гаусса онлайн.
2. Точка пересечения прямых, заданных в каноническом виде.
Пусть задана декартова прямоугольная система координат Oxy и пусть в этой системе координат заданы прямые L1 и L2:
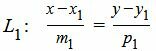 | (6) |
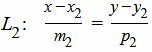 | (7) |
Приведем уравнение L1 к общему виду. Сделаем перекрестное умножение в уравнении (6):
| p1(x−x1)=m1(y−y1) |
Откроем скобки и сделаем преобразования:
| p1x−m1y−p1x1+m1y1=0 |
| A1x+B1y+C1=0 | (8) |
Аналогичным методом получим общее уравнение прямой (7):
| A2x+B2y+C2=0 | (9) |
Терерь можно найти точку пересечения прямых L1 и L2 методом, описанным в параграфе 1.
3. Точка пересечения прямых, заданных в параметрическом виде.
Пусть задана декартова прямоугольная система координат Oxy и пусть в этой системе координат заданы прямые L1 и L2 в параметрическом виде:
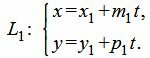 | (10) |
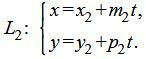 | (11) |
Приведем уравнение прямой L1 к каноническому виду. Для этого из уравнений (10) найдем параметр t:
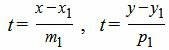 | (12) |
Из уравнений (12) следует:
 |
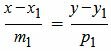Аналогичным образом можно найти каноническое уравнение прямой L2:
 |
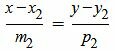Как найти точку пересечения прямых, заданных в каноническом виде описано выше.
4. Точка пересечения прямых, заданных в разных видах.
Пусть задана декартова прямоугольная система координат Oxy и пусть в этой системе координат заданы прямые L1 и L2:
| L1: A1x+B1y+C1=0, | (13) |
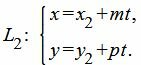 | (14) |
| A1(x2+mt)+B1(y2+pt)+C1=0, | (15) |
| A1x2+A1mt+B1y2+B1pt+C1=0, |
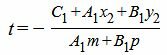 | (16) |
Если числитель и знаменатель в (16) одновременно равны нулю, то любое значение t удовлетворяет уравнению (15), следовательно прямые L1 и L2 совпадают. Если знаменатель равен нулю а числитель отличен от нуля, то прямые L1 и L2 не пересекаются, т.е. они параллельны.
Пусть знаменатель не равен нулю. Подставляя полученное значение t в (14), получим координаты точки пересечения прямых L1 и L2.
5. Примеры нахождения точки пересечения прямых на плоскости.
Пример 1. Найти точку пересечения прямых L1 и L2:
| L1: 2x+y+4=0, | (17) |
| L2: x−3y+2=0. | (18) |
Для нахождения точки пересечения прямых L1 и L2 нужно решить систему линейных уравнений (17) и (18). Представим уравнения в матричном виде:
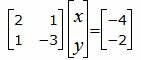 | (19) |
Решим систему линейных уравнений отностительно x, y. Для этого воспользуемся методом Гаусса. Получим:
 |
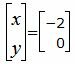Ответ. Точка пересечения прямых L1 и L2 имеет следующие координаты:
Пример 2. Найти точку пересечения прямых L1 и L2:
| L1: 2x+3y+4=0, | (20) |
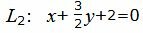 | (21) |
Для нахождения точки пересечения прямых L1 и L2 нужно решить систему линейных уравнений (20) и (21). Представим уравнения в матричном виде:
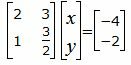 | (22) |
Для решения (22) воспользуемся методом Гаусса. Получим:
 |
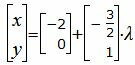где λ− произвольное действительное число.
Имеем больше одного решения. Это означает, что прямые L1 и L2 совпадают.
Пример 3. Найти точку пересечения прямых L1 и L2:
| L1: −5x+y+9=0, | (23) |
| L2: −10x+2y−3=0, | (24) |
Для нахождения точки пересечения прямых L1 и L2 нужно решить систему линейных уравнений (23) и (24). Представим уравнения в матричном виде:
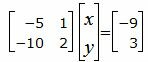 | (25) |
Применив метод Гаусса получим, что система (25) несовместна. Следовательно эти прямые не пересекаются, т.е. они параллельны.
Ответ. Прямые L1 и L2 не имеют общую точку, т.е. они параллельны.
Пример 4. Найти точку пересечения прямых L1 и L2:
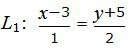 | (26) |
| L2: x+2y−9=0, | (27) |
Приведем, сначала, уравнение прямой (26) к общему виду:
Для нахождения точки пересечения прямых L1 и L2 нужно решить систему линейных уравнений (28) и (27). Представим уравнения в матричном виде:
 | (29) |
Решим систему линейных уравнений отностительно x, y:
 |
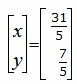Ответ. Точка пересечения прямых L1 и L2 имеет следующие координаты:
Видео:Точки пересечения графиков линейных функций. 7 класс.ОбразовательныйСкачать
Пересечение с осями онлайн
Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha, предназначен для решения задачи нахождения точек пересечения графика функции с осями координат.
Найти точки пересечения функции с осями координат:
При проведении исследования функции, возникает задача нахождения точек пересечения этой функции с осями координат. Рассмотрим на конкретном примере алгоритм решения такой задачи. Для простоты будем работать с функцией одной переменной:
График данной функции представлен на рисунке:
Как следует из рисунка, наша функция пересекает ось в двух точках, а ось — в одной.
Сначала найдём точки пересечения функции с осью . Сразу отметим, что в этих точках координата . Поэтому для их поиска, нам нужно решить уравнение:
Таким образом, мы нашли две точки пересечения нашей функции с осью абсцисс: и . Стоит отметить, что задача поиска пересечений функции с осью эквивалентна задаче нахождения нулей функции.
Теперь найдём точку пересечения с осью ординат. В этой точке координата . Поэтому для их поиска, просто подставляем значение в нашу функцию:
Таким образом, мы нашли точку пересечения нашей функции с осью ординат .
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать
Другие полезные разделы:
Видео:Пересечения прямых, лучей, отрезковСкачать
Оставить свой комментарий:
Мы в социальных сетях:
Группа ВКонтакте | Бот в Телеграмме
🌟 Видео
ПЕРЕСЕЧЕНИЕ прямых | ТОЧКА пересечения | Линейные функцииСкачать
Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать
Составляем уравнение прямой по точкамСкачать
Как найти точку пересечения двух прямых в пространстве?Скачать
6 класс, 23 урок, Пересечение прямыхСкачать
Пересечение прямой и плоскостиСкачать
Найти координаты точки пересечения прямыхСкачать
Не выполняя построения графиков, найдите координаты точки пересечения прямых. Алгебра 7 класс.Скачать
Задача 13. Найти точку пересечения прямой и плоскости.Скачать
Лекция 2. Основная задача начертательной геометрии. Точка пересечения прямой с плоскостью.Скачать
Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать
Стереометрия 10 класс. Часть 1 | МатематикаСкачать
Задание 23 из ОГЭ Построение графиков функций с модулем | МатематикаСкачать
Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать
