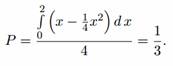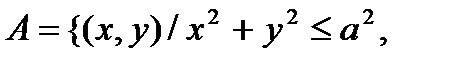Готовое решение: Заказ №8391
Готовое решение: Заказ №8391 




Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.
Кстати, если эта работа не по вашей теме или не по вашим данным , не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу , я смогу выполнить её в срок 1-3 дня!
Описание и исходные данные задания, 50% решения + фотография:
В квадрате с вершинами (0; 0), (0; 2), (2; 2) и (2; 0) наудачу берётся точка (x, y). Какова вероятность того, что xy 2 ).
Пусть событие A – произведение координат точки M меньше 1 ().
Событию A благоприятствуют все точки квадрата, которые отвечают неравенству:
| Изучите математику на странице ➔ решение заданий и задач по математике. |
| Похожие готовые решения: |
- Наудачу взяты 2 положительных числа X и Y, каждое из которых не превышает единицы. Найти вероятность того, что сумма X+Y не превышает единицы, а произведение XY не меньше 0,5.
- Из отрезка [0; 10] наудачу взяты два числа. Какова вероятность того, что сумма их квадратов меньше 41, а произведение больше 20?
- Внутри квадрата с вершинами (0; 0), (1; 0), (1; 1), (0; 1) наудачу выбирается точка M(x; y). Найти вероятность того, что произведение координат xy не превосходит 0,5.
- С какой вероятностью одно из двух чисел, выбранных наудачу из отрезка [0; 2] меньше квадрата другого числа?
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Видео:Теория вероятностей | Математика TutorOnlineСкачать

Геометрическая вероятность
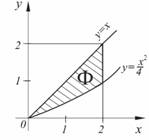
Пример №1 . Из промежутка [0; 2] наудачу выбраны два числа x и y. Найдите вероятность того, что эти числа удовлетворяют неравенствам x 2 ≤ 4y ≤ 4x.
Решение. Испытание состоит в случайном выборе из промежутка [0; 2] пары чисел x и y. Будем это интерпретировать как выбор наудачу точки M(x;y) из множества всех точек квадрата, сторона которого равна двум. Рассмотрим фигуру Ф, представляющую собой множество всех точек квадрата, координаты которых удовлетворяют системе неравенств x 2 ≤ 4y ≤ 4x. Интересующее событие происходит тогда и только тогда, когда выбранная точка M(x;y) принадлежит фигуре Ф.
По формуле (8) искомая вероятность равна отношению площади фигуры Ф к площади квадрата:
Пример №2 . Двое договорились о встрече в определенном месте. Каждый из них приходит в условленное место независимо друг от друга в случайный момент времени из [0;T] и ожидает не более чем время 
Решение. Обозначим через x время прихода первого в условленное место, а через y — время прихода туда второго лица. Из условия вытекает, что x и y независимо друг от друга пробегают промежуток времени [0;T]. Испытание состоит в фиксации времени прихода указанных лиц к месту встречи. Тогда пространство элементарных исходов данного испытания интерпретируется как совокупность всех точек M(x;y) квадрата Ω=. Интересующее нас событие A — “встреча произошла” наступает в том и только том случае, когда выбранная точка M(x;y) окажется внутри фигуры Ф, представляющей собой множество всех точек квадрата, координаты которых удовлетворяют неравенству |x – y| ≤ t. По формуле (8) искомая вероятность
представляет собой отношение площади фигуры Ф к площади квадрата Ω:
Пример №3 . На отрезке l наугад выбраны две точки.
P(0 k-l
Пример №4 . В круг радиуса r случайным образом брошена точка так, что любое ее расположение в круге равновозможно. Найти вероятность того, что она окажется внутри находящегося в круге квадрата со стороной a.
Решение. Вероятность того, что точка окажется внутри лежащего в круге квадрата со стороной а будет равна отношению площади квадрат к площади круга.
Площадь квадрата: Sкв = a 2 .
Площадь круга: S = πr 2
Тогда вероятность составит: p = Sкв / S = a 2 / πr 2
Пример №5 . С промежутке [0, 4] выбирают наугад два действительных числа. Найдите вероятность того, что их сумма будет больше 4, а произведение — меньше 4.
Решение.
Всего чисел 5: 0,1,2,3,4. Вероятность их появления p=1/5 = 0.2
а) вероятность того, что их сумма будет больше 4
Всего количество таких исходов равно 8:
1+4, 2+3, 2+4, 3+4 и 4+1, 3+2, 4+2, 4+3
P = 0.2*0.2*8 = 0.32
б) произведение — меньше 4.
Всего количество таких исходов равно 13:
0*1, 0*2, 0*3, 0*4, 1*1, 1*2,1*3 и 1*0, 2*0, 3*0, 4*0, 2*1, 3*1
P = 0.2*0.2*13 = 0.52
Задачи для самостоятельного решения
4.3. После бури на участке между 40-м и 70-м километрами телефонной линии произошел обрыв провода. Какова вероятность того, что разрыв произошел между 45-м и 50-м километром линии? (Вероятность обрыва провода в любом месте считать одинаковой).
Ответ: 1/6.
4.4. В круг радиуса r наугад брошена точка. Найдите вероятность того, что эта точка окажется внутри вписанного в данный круг правильного треугольника.
Ответ:
4.5. Найдите вероятность того, что сумма двух случайно выбранных чисел из промежутка [-1; 1] больше нуля, а их произведение отрицательно.
Ответ: 0;25.
4.6. Во время боевой учебы н-ская эскадрилья бомбардировщиков получила задание атаковать нефтебазу “противника”. На территории нефтебазы, имеющей форму прямоугольника со сторонами 30 и 50 м, находятся четыре круглых нефтебака диаметром 10 м каждый. Найдите вероятность прямого поражения нефтебаков бомбой, попавшей на территорию нефтебазы, если попадание бомбы в любую точку этой базы равновероятно.
Ответ: π/15.
4.7. Два действительных числа x и y выбираются наудачу так, что сумма их квадратов меньше 100. Какова вероятность, что сумма квадратов этих чисел окажется больше 64?
Ответ: 0;36.
4.8. Двое друзей условились встретиться между 13 и 14 часами. Пришедший первым ждет второго в течение 20 минут, после чего уходит. Определите вероятность встречи друзей, если моменты их прихода в указанном промежутке времени равновозможны.
Ответ: 5/9.
4.9. Два парохода должны подойти к одному и тому же причалу. Время прихода обоих пароходов равновозможно в течение данных суток. Определите вероятность того, что одному из пароходов придется ожидать освобождения причала, если время стоянки первого парохода равно одному часу, а второго — двум часам.
Ответ: ≈ 0;121.
4.10. Наудачу взяты два положительных числа x и y, каждое из которых не превышает двух. Найдите вероятность того, что произведение x · y будет не больше единицы, а частное y/x не больше двух.
Ответ: ≈ 0;38.
4.11. В области G, ограниченной эллипсоидом 
Ответ: 1/3.
4.12. В прямоугольник с вершинами R(-2;0), L(-2;9), M (4;9), N (4;0) брошена точка. Найдите вероятность того, что ее координаты будут удовлетворять неравенствам 0 ≤ y ≤ 2x – x 2 +8.
Ответ: 2/3.
4.13. Область G ограничена окружностью x 2 + y 2 = 25, а область g — этой окружностью и параболой 16x — 3y 2 > 0. Найдите вероятность попадания в область g.
Ответ: ≈ 0;346.
4.14. Наудачу взяты два положительных числа x и y, каждое из которых не превышает единицы. Найдите вероятность того, что сумма x + y не превышает единицы, а произведение x · y не меньше 0,09.
Ответ: ≈ 0;198.
Видео:Математика без Ху!ни. Теория вероятностей, комбинаторная вероятность.Скачать

Геометрическая вероятность
Пусть W — множество точек отрезка или ограниченной плоской фигуры, А – заданное подмножество множества W. Будем считать, что испытание состоит в случайном выборе точки этого множества , событие А – выбор точки из подмножества А, причем «попадание» точки в каждую элементарную часть DW одной и той же длины или площади равновозможно. Тогда вероятность случайного события А будет определена по формуле
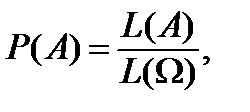
где L(A) – длина отрезка А, L(W) – длина отрезка W,
S(A) – площадь плоской фигуры А, S(W) – площадь фигуры W.
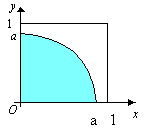
Пример 1. Внутри квадрата с вершинами (0;0), (1;0), (1;1), (0;1) наудачу выбирается точка М (х, у). Найти вероятность события
Решение. Пусть М(х,у) — случайная точка, попавшая внутрь квадрата со стороной 1 и круга с центром в начале координат радиуса а (рис. 5.1). Так как 

Пример 2. Найти вероятность того, что корни квадратного уравнения 
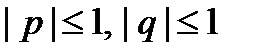
Решение. Областью всех возможных пар значений (p , q) является квадрат ABCD с центром в начале координат и стороной, равной 2 (рис. 5.2). Значит, 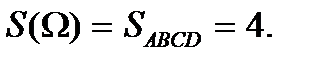

ограниченной сверху кривой 
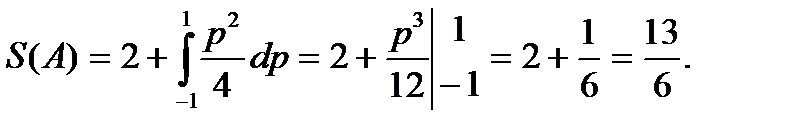
Пример 3. Наугад взяты два положительных числа х и у, каждое из которых не превышает 2. Найти вероятность того, что их произведение не меньше 2, а сумма не больше 3.
Решение. Так как числа х и у удовлетворяют условиям 0 ≤ х ≤ 2 и 0 ≤ у ≤ 2, то точки М(х, у), удовлетворяющие этим условиям, образуют квадрат со стороной 2 и площадью S D = 4.
Найдем множество М(х, у) для которых ху ≥ 2 и х + у ≤ 3. Эти точки, удовлетворяющие указанной системе неравенств, образуют область d, ограниченной гиперболой ху = 2 и прямой х + у = 3 (рис. 5.3). Находим площадь S d области d:
=
5.1. Два теплохода должны подойти к одному и тому же причалу. Время прихода обоих теплоходов независимо и равновозможно в течение данных суток. Определить вероятность того, что одному из них придется ожидать освобождения причала, если время стоянки первого теплохода – один час, а второго – 2 часа.
5.2. Противник в течение часа делает один десятиминутный налет на участок шоссе. В течение этого же часа нужно преодолеть этот опасный участок шоссе. Какова вероятность того, что можно избежать налета, если время преодоления опасного участка пять минут?
5.3. Два человека договорились о встрече в определенном месте в промежутке времени от 19. 00 до 20. 00. Каждый из них приходит наудачу, независимо от другого и ожидает 15 минут. Какова вероятность того, что они встретятся?
5.4. Два студента условились встретиться между 12 и 13 часами дня. Пришедший первым ждет второго в течение 10 минут, после чего уходит. Какова вероятность того, что встреча состоится?
5.5. Внутрь круга радиуса R наудачу брошена точка. Найти вероятность того, что точка окажется внутри вписанного в круг: а) квадрата; б) правильного треугольника?
5.6. На площадку, покрытую кафельной плиткой со стороной а = 6см, случайно падает монета радиуса r = 2см. Какова вероятность того, что монета целиком окажется внутри квадрата?
5.7. На отрезке [0,3] наудачу выбраны два числа х и у. Какова вероятность того, что эти числа удовлетворяют неравенствам х 2 ≤ 3у ≤ 3х?
5.8. Наудачу выбирают два числа из промежутка [0, 1]. Какова вероятность того, что их сумма заключена между 1/4 и 1?
5.9. Наудачу взяты два положительных числа х и у, каждое из которых не превышает двух. Какова вероятность того, что произведение х · у будет не больше 1, а частное у/х не больше двух?
5.10. Наудачу взяты два положительных числа х и у, каждое из которых не превышает единицы. Какова вероятность того, что сумма х + у будет не превышает 1, а произведение х · у не меньше 0,09?
5.11. На плоскости нарисованы две концентрические окружности, радиусы которых 3 и 5 см. Какова вероятность того, что точка брошенная наудачу в больший круг, попадет в кольцо, образованное этими окружностями?
5.12. На перекрестке установлен светофор, в котором в течение 25 секунд горит зеленый свет, 19 секунд горит красный свет, а в промежутках между ними в течение 3 секунд – желтый свет. Какова вероятность того, что автомобиль, случайно подъехавший к перекрестку, проедет его без остановки?
5.13. Внутри эллипса 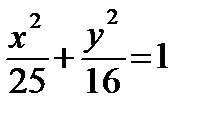
5.14. В квадрат с вершинами в точках О(0, 0), К(0, 1), L(1, 1), М(1, 0) наудачу брошена точка. Какова вероятность того, что координаты этой точки удовлетворяют неравенству 
5.15. В эллипс 
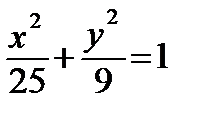
5.16. На отрезке [0, 2] наудачу выбраны два числа х и у. Какова вероятность того, что эти числа удовлетворяют неравенствам х 2 ≤ 4у ≤ 4х?
5.17. Круг разделен на 6 равных секторов, через один окрашенный в черный цвет. Какова вероятность того, что точка брошенная в круг попадет в белый сектор?
5.18. Взяты наугад два положительных числа, каждое из которых не больше единицы. Какова вероятность того, что их сумма не превзойдет единицы, а произведение будет не больше 2/9?
5.19. В прямоугольник с вершинами К(-1, 0), L(-1, 5), М(2, 5), N(2, 0) брошена точка. Какова вероятность того, что ее координаты будут удовлетворять неравенствам х 2 +1 ≤ у ≤ х + 3?
5.20. В квадрат с вершинами О(0, 0), К(0, 1), L(1, 1), М(1, 0) наудачу брошена точка. Какова вероятность того, что координаты этой точки удовлетворяют неравенству у > 2x?
5.21. На плоскости область G ограничена эллипсом 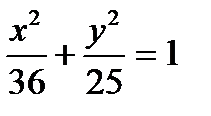

5.22. В прямоугольник с вершинами К(-2, 0), L(-2, 5), М(1, 5), N(1, 0) брошена точка. Какова вероятность того, что ее координаты будут удовлетворять неравенствам х 2 +1 ≤ у ≤ х — 3?
5.23. В прямоугольник с вершинами R(-2, 0), L(-2, 5), M(1, 5), N(1, 0) брошена точка. Какова вероятность того, что ее координаты будут удовлетворять неравенствам 0 ≤ у ≤ 2х – х 2 + 8?
5.24. Внутрь круга радиусом R наудачу брошена точка. Какова вероятность того, что точка окажется внутри вписанного в круг правильного шестиугольника?
5.25. Внутрь равностороннего треугольника со стороной а брошена точка. Какова вероятность того, что точка попадет в круг, вписанный в треугольник?
5.26. Наугад взяты два положительных числа х и у, каждое из которых не превышает 2. Какова вероятность того, что их произведение не меньше 2, а сумма не больше 3?
5.27. Внутрь круга радиусом R наудачу брошена точка. Какова вероятность того, что точка окажется в области между кругом и вписанным в него квадратом?
5.28. В квадрат вписан круг. Какова вероятность того, что точка, брошенная в квадрат, попадет внутрь вписанного в него круга?
5.29. На отрезке АВ длины L числовой оси Ох наудачу нанесена точка М(х). Какова вероятность того, что отрезки АМ и МВ имеют длину, большую L/4?
5.30. На отрезке L длины 20 см помещен меньший отрезок l длины 10 см. Какова вероятность того, что точка, наудачу поставленная на больший отрезок, попадет также и на наименьший отрезок?
ОТВЕТЫ: 5.1. 0,121. 5.2. 0,77. 5.3. 7/16. 5.4. 0,3056. 5.5. 
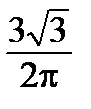
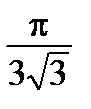
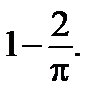
Последнее изменение этой страницы: 2019-03-29; Просмотров: 1969; Нарушение авторского права страницы
📺 Видео
Геометрическая вероятность. С какой вероятностью можно составить треугольникСкачать

Задача о встречеСкачать

Геометрическая вероятностьСкачать

ВСЕ ТИПЫ 20 ЗАДАНИЕ 2 ЧАСТЬ ОГЭ МАТЕМАТИКА 2023Скачать

Геометрическая вероятностьСкачать

Задача №29. Выбор случайной точки внутри прямоугольника. Геометрическая вероятность.Скачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Геометрическая вероятностьСкачать

Геометрическая вероятностьСкачать

11 класс, 22 урок, Вероятность и геометрияСкачать

Геометрические вероятностиСкачать

Уравнения с модулем. Разбор 22 задания из ОГЭ | Математика 9 класс | TutorOnlineСкачать

ОСНОВЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ Урок 5. Геометрическая вероятность. Решение задачСкачать

На отрезке [‐7;18] числовой оси случайным образом отмечают одну точку. Найти вероятность того,что..Скачать
![На отрезке [‐7;18] числовой оси случайным образом отмечают одну точку. Найти вероятность того,что..](https://i.ytimg.com/vi/7DDd-0aNjIU/0.jpg)
Геометрическая вероятностьСкачать

Задание 23 из ОГЭ Построение графиков функций с модулем | МатематикаСкачать

ТЕОРИЯ ВЕРОЯТНОСТИ С ТИНДЕРОМ 😉 #shorts #егэ #огэ #математика #профильныйегэСкачать

ПОЛНЫЙ РАЗБОР ДЕМОВЕРСИИ ОГЭ ПО МАТЕМАТИКЕ 2024Скачать