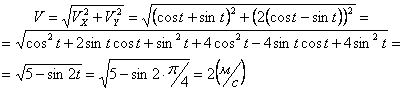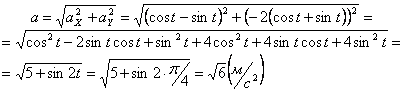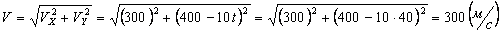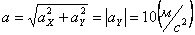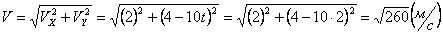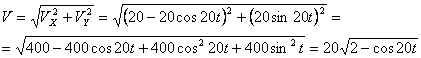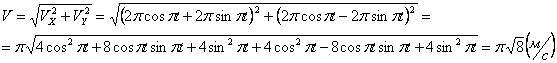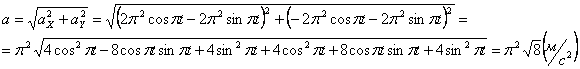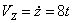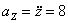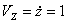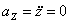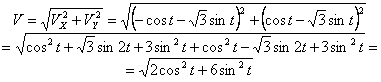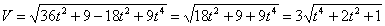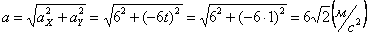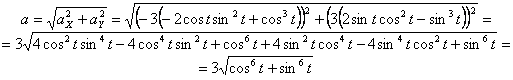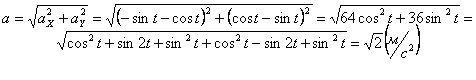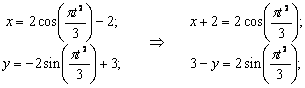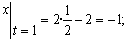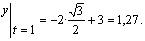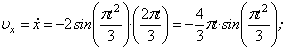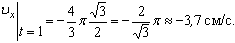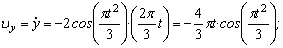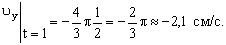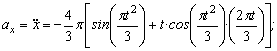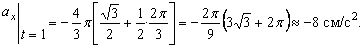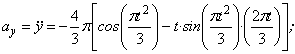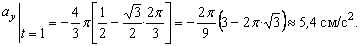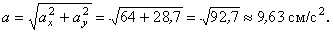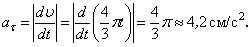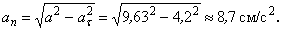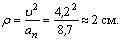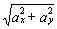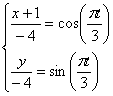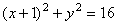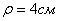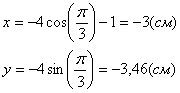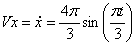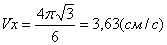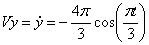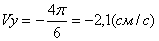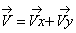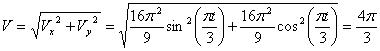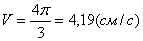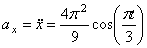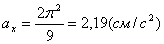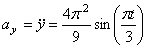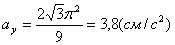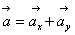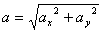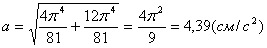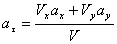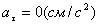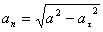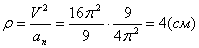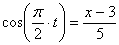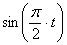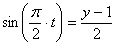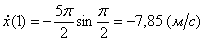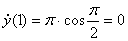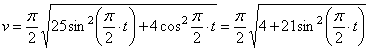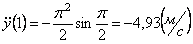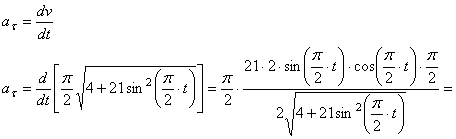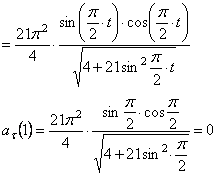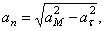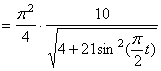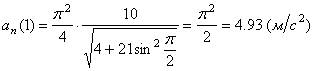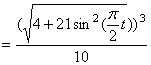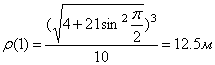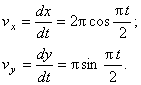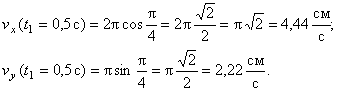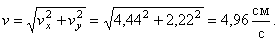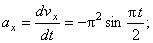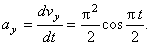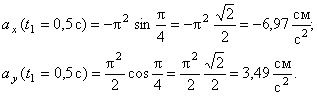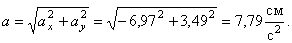Точка движется в плоскости xoy согласно уравнениям x 3t y 4t2 определить ускорение точки

Нужно решить задачи К-1 и Д 2

4.1.1. К -1. Определение скорости и ускорения

точки по заданным уравнениям её движения

Определить: уравнение траектории точки; для момента времени t1=1с найти скорость и ускорение точки, а также её касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.

Указания: задача К1 относится к кинематике точки; скорость и ускорение точки в декартовых координатах определяются по формулам координатного способа задания движения точки, а касательное и нормальное ускорения точки — по формулам естественного способа задания её движения.

По предпоследней цифре шифра зачетной книжки выбирается уравнение, задающее изменении координаты X(t), а по последней – Y(t).

В задаче все искомые величины следует определить для момента времени t1=1с.

Дано: уравнения движения точки в плоскости XOY:

Определить: уравнение траектории точки; для момента времени t1=1с найти скорость и ускорение точки, а также её касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.

1. Для определения уравнения траектории точки исключим из данных уравнений движения параметр t:

— уравнение траектории точки – эллипс с полуосями 12 см и 4 см (рис. К -1).

2. Определим положение точки на траектории в момент времени t1=1с :

3. Скорость точки находим по её проекциям на координатные оси:

, при t1=1с

2. Аналогично найдём ускорение точки при t1=1с :

, при t1=1с

5. Находим касательное ускорение точки, зная численные значения всех величин, входящих в правую часть выражения:

при t1=1с

6. Нормальное ускорение точки определяем по формуле , подставляя известные численные значения. При t1=1с получим

5.3.3. Д -2. Применение теоремы об изменении кинетической энергии

к изучению движения механической системы

два вариант 2 и 3

Дано. Механическая система состоит из катков 1 и 2 (или катка и подвижного блока), ступенчатого шкива 3 с радиусами ступеней R3= 0,3 м, r3 = 0,1 м и радиусом инерции относительно оси вращения ρ3 = 0,2 м, блока 4 радиуса R4= 0,2 м и грузов 5 и 6 (рис. Д 2.0 – Д 2.9, табл. Д-2); тела 1 и 2 считать сплошными однородными цилиндрами, а массу блока 4 – равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f=0,1. Тела системы соединены друг с

другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с.

Под действием силы F=f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сил сопротивления (от трения в подшипниках).

Все катки катятся по плоскостям без скольжения.

Если по заданию массы грузов 5 и 6 или массы катков 1 (рис. Д 2.0-2.4) и 2 (рис. Д 2.5-2.9) равны нулю, то на чертеже их можно не изображать.

Определить: значение искомой величины в тот момент времени, когда перемещение s станет равным s1= 0,2 м. Искомая величина указана в столбце «Найти» таблицы Д 2, где обозначено: ω3 – угловая скорость тела 3; ε4 – угловое ускорение тела 4; v5 – скорость тела 5; ас2- ускорение центра масс тела 2 и т. п.

Указания. При решении задачи учесть, что кинетическая энергия системы равна сумме кинетических энергий всех входящих в систему тел; эту энергию следует выразить через ту скорость (линейную или угловую), которую в задаче надо определить. При вычислении энергии для установления зависимости между скоростями точек тела, движущегося плоскопараллельно, или между его угловой скоростью и скоростью центра масс воспользоваться мгновенным центром скоростей. При вычислении работы необходимо все перемещения выразить через заданное перемещение s1, учитывая при этом, что зависимость между перемещениями здесь будет такой же, как между соответствующими скоростями.

Видео:Траектория и уравнения движения точки. Задача 1Скачать

Точка движется в плоскости xoy по закону: x  2sint ; y  2cost .

👉 Как получить работу? Ответ: Напишите мне в whatsapp и я вышлю вам форму оплаты, после оплаты вышлю решение.

➕ Как снизить цену? Ответ: Соберите как можно больше задач, чем больше тем дешевле, например от 10 задач цена снижается до 50 руб.

➕ Вы можете помочь с разными работами? Ответ: Да! Если вы не нашли готовую работу, я смогу вам помочь в срок 1-3 дня, присылайте работы в whatsapp и я их изучу и помогу вам.

⚡ Условие + 37% решения:

Точка движется в плоскости xoy по закону: x  2sint ; y  2cost . Найти путь, пройденный телом за 2с; угол между векторами скорости  и ускорения a ; траекторию движения y=f (x).

Решение Согласно условию задачи точка движется в плоскости xoy по закону: x  2sint y  2cost Эти уравнения перепишем в другом виде: x t 2 2  4sin y t 2 2  4cos Из последних двух уравнений можем записать: x y t t 2 2 2 2   4sin  4cos x y  t t 2 2 2 2   4 sin  cos 4 2 2 x  y  Или: 2 2 2 x  y  2 Получили уравнение окружности с центром в точке 0; 0 и радиуса R  2 м . Найдем скорости x и y :   t dt d t dt dx x     2 cos 2sin    (1)   t dt d t dt dy y     2 sin 2cos     (2) Тогда скорость  будет равна:    2 cos   2sin  2 cos  sin  2 2 2 2 2 2 2  x  y  t   t  t  t  (3)

Готовые задачи по физике которые сегодня купили:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Видео:Кинематика точки Задание К1Скачать

Точка движется в плоскости xoy согласно уравнениям x 3t y 4t2 определить ускорение точки

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО КИНЕМАТИКЕ

7.1. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .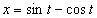

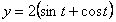
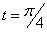
Решение: Скорости точки :

,

,

,

,

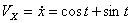
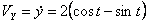
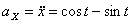
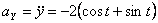
Модуль полного ускорения:

Модуль касательного ускорения точки:

,

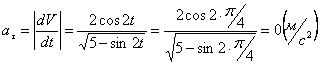
А модуль нормального ускорения:

.

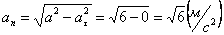
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

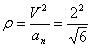
7.2. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .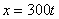

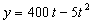
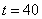
Решение: Скорости точки :

,

,

,

,

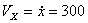
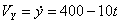
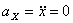
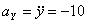
Модуль полного ускорения:

Модуль касательного ускорения точки:

,

А модуль нормального ускорения:

.

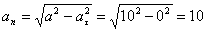
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

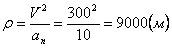
7.3. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .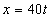

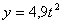
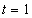
Решение: Скорости точки:

,

,

.

,

,

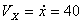
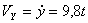
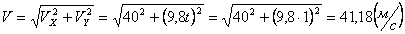
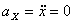
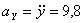
Модуль полного ускорения:

.

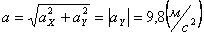
Модуль касательного ускорения точки:

,

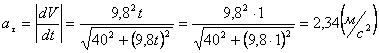
А модуль нормального ускорения:

.

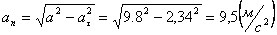
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

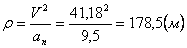
7.4. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .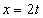

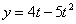
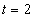
Решение: Скорости точки :

,

,

,

,

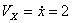
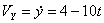
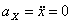
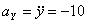
Модуль полного ускорения:

Модуль касательного ускорения точки:

,

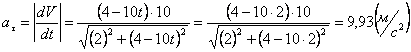
А модуль нормального ускорения:

.

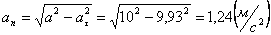
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

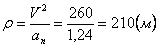
7.5. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .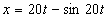

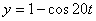
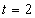
Решение: Скорости точки по осям :

,

,

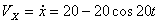
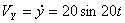
Ускорения точки по осям:

,

,

.

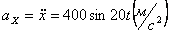
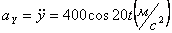
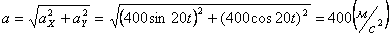
Модуль касательного ускорения точки:

, а модуль нормального ускорения .

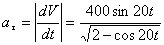
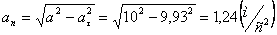
Нормальное ускорение и радиус кривизны траектории связаны соотношением .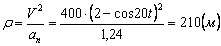

7.6. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .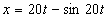

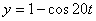
Решение: Скорости точки по осям :

,

,

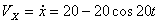
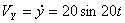
Ускорения точки по осям:

,

,

.

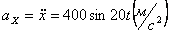
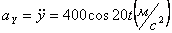
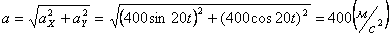
Модуль касательного ускорения точки:

,

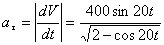
а модуль нормального ускорения:

.

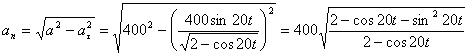
Нормальное ускорение и радиус кривизны траектории связаны соотношением .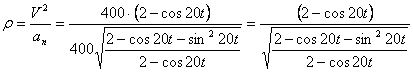

7.7. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .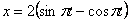

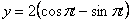
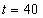
Решение: Скорости точки :

,

,

,

,

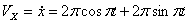
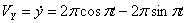
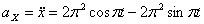
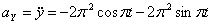
Модуль полного ускорения:

Модуль касательного ускорения точки:

,

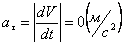
А модуль нормального ускорения:

.

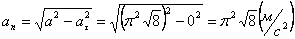
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

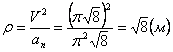
7.8. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .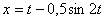

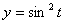
Решение: Скорости точки :

,

,

.

,

,

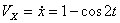
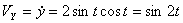
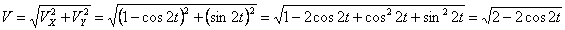
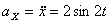
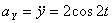
Модуль полного ускорения:

.

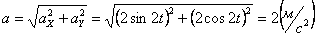
Модуль касательного ускорения точки:

,

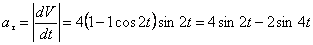
А модуль нормального ускорения:

.

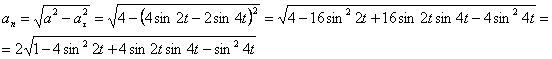
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

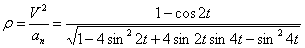
7.9. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , , .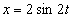

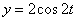
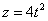
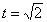
Решение: Скорости точки :

,

,

.

,

,

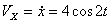
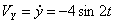
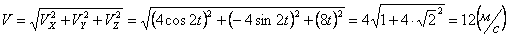
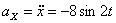
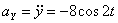
Модуль полного ускорения:

.

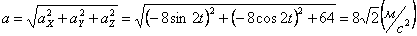
Модуль касательного ускорения точки:

,

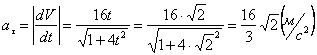
А модуль нормального ускорения:

.

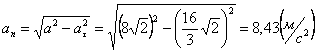
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

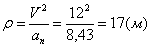
7.10. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .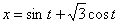

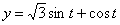
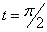
Решение: Скорости точки :

,

,

,

,

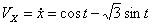
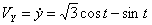
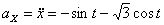
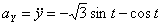
Модуль полного ускорения:

Модуль касательного ускорения точки:

,

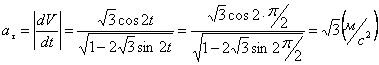
А модуль нормального ускорения:

.

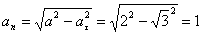
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

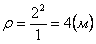
7.11. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .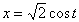

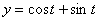
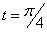
Решение: Скорости точки :

,

,

,

,

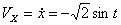
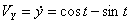
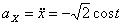
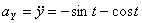
Модуль полного ускорения:

Модуль касательного ускорения точки:

,

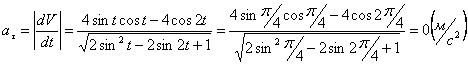
А модуль нормального ускорения:

.

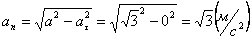
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

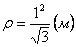
7.12. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , , .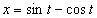

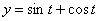
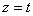
Решение: Скорости точки :

,

,

,

,

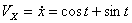
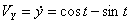
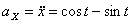
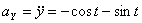
Модуль полного ускорения:

Модуль касательного ускорения точки:

,

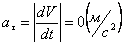
А модуль нормального ускорения:

.

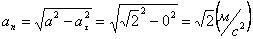
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

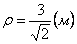
7.13. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .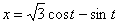

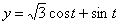
Решение: Скорости точки :

,

,

,

,

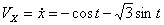
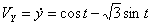
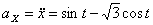
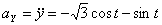
Модуль полного ускорения:

Модуль касательного ускорения точки:

,

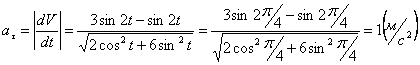
А модуль нормального ускорения:

.

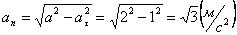
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

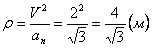
7.14. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .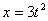

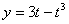
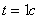
Найти: , , .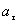

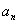
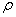
Решение: Скорости точки по осям :

,

,

,

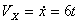
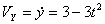
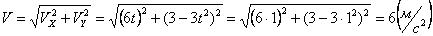
Ускорения точки по осям:

,

,

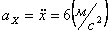
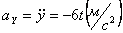
Модуль касательного ускорения точки:

,

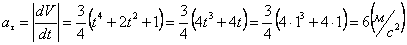
А модуль нормального ускорения:

.

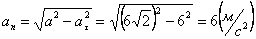
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

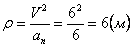
7.15. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .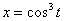

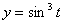
Решение: Скорости точки :

,

,

,

,

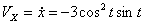
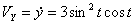
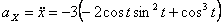
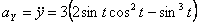
Модуль полного ускорения:

Модуль касательного ускорения точки:

,

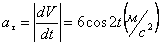
А модуль нормального ускорения:

.

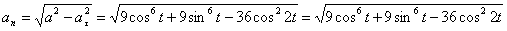
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

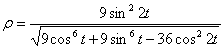
7.16. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .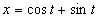

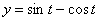
Решение: Скорости точки :

,

,

,

,

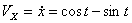
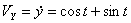
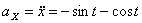
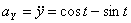
Модуль полного ускорения:

Модуль касательного ускорения точки:

,

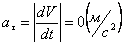
А модуль нормального ускорения:

.

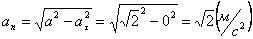
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

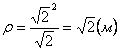
7.17. Определить касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

Дано: , , .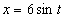

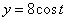
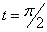
Решение: Скорости точки :

,

,

,

,

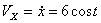
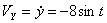
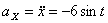
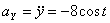
Модуль полного ускорения:

Модуль касательного ускорения точки:

,

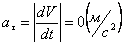
А модуль нормального ускорения:

.

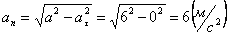
Нормальное ускорение и радиус кривизны траектории связаны соотношением:

.

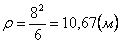
7.18. Дан закон движения точки по окружности радиусом r . Определить:

1) скорость и ускорение точки при 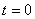и ;

2) моменты остановки точки;

3) путь, пройденный точкой за 10секунд.

Дано: , , , .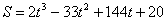

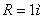
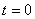
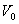
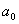
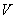
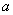
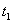
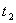
Найти: , , , , , , П.

Решение: 1. На траектории отметим точку О – начало отсчета координаты s и укажем положительное направление отсчета этой координаты. Отметим положение точки в заданные моменты времени: При :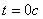

;

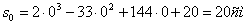
При :

.

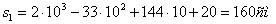
Проведем из этих точек естественные оси координат.

Определим проекцию скорости на касательную:

.

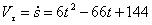
При : ;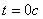

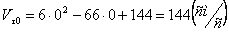
При : .

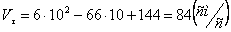
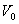
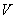
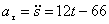
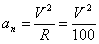
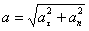
Векторы и совпадают со своими проекциями. Определим проекции ускорения на естественнее оси координат :

; , Полное ускорение точки .

При :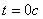

,

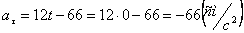
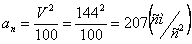
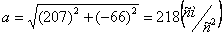
и

.

При :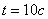

,

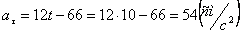
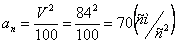
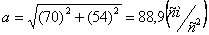
и

.

2. Чтобы найти время остановки надо найти время, когда скорость точки равна нулю:

, получим и .

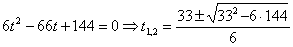
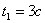
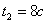
3. Поскольку за 10 секунд точка сделала две остановки, пройденный ею путь за 10с можно найти как сумму пути, пройденного от начала до первой остановки, от первой до второй остановки и от второй до момента времени :

,

; ; ; .

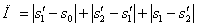
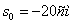
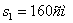
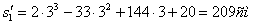
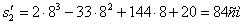
Путь пройденный точкой за 10 секунд:

.

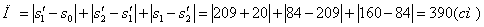
7.19. Определить скорость, касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

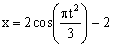
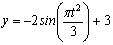
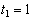
Дано: , (1)

( x и y – в см , t и t ₁ – в с).

Найти: 1) вид траектории;

2) для t = t ₁ положение точки на траектории;

3) .

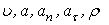
Решение: 1) Уравнение движения (1) можно рассматривать как параметрические уравнения траектории точки. Чтобы получить уравнения траектории в координатной форме, исключаем время t из уравнений (1).

Возводя обе части равенств в квадрат, а затем складывая равенства, получаем 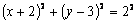, т.е. траекторией точки М является окружность радиуса 2, показанная на рис.1.

2) Определяем положение точки М в заданный момент времени t =1 с :

Вектор скорости точки

. (2)

(3)

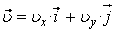
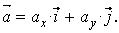
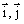
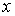
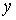
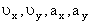
Здесь – орты осей и ; – проекции скорости и ускорения точки на оси координат.

Найдем их, дифференцируя по времени уравнения движения (1):

По найденным проекциям определяем модуль скорости:

, (4)

,

,

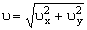
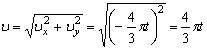
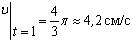
и модуль ускорения точки:

, (5)

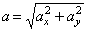
Модуль касательного ускорения точки

, (6)

; (7)

выражает проекцию ускорения точки на направление ее скорости. Знак «+» при означает, что движение точки ускоренное, направление и совпадают; знак «–» – что движение замедленное.

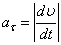
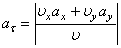
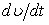
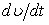
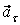
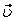
Вычисляем модуль касательного ускорения для заданного момента времени

Модуль нормального ускорения точки

. (8)

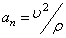
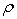
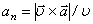
Если радиус кривизны траектории в рассматриваемой точке неизвестен, то нормальное ускорение можно определить по формуле

. (9)

При движении точки в плоскости формула (9) принимает вид

.

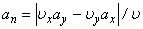
Модуль нормального ускорения можно определить и следующим образом:

. (10)

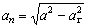
Воспользуемся в нашем случае формулой (10)

Радиус кривизны траектории в рассматриваемой точке определим из выражения:

. (11)

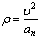
Тогда

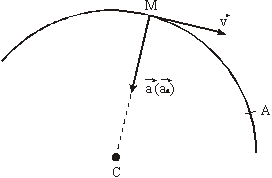
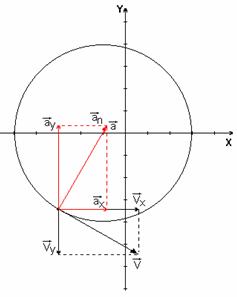
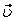
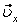
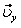
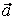
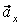
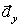
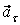
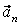
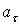
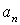
На рис. 1 показано положение точки М в заданный момент времени. Вектор строим по составляющим и , причем этот вектор должен по направлению совпадать с касательной к траектории. Вектор строим по составляющим и и затем раскладываем на составляющие и . Совпадение величин и , найденных из чертежа, с их значениями, полученными аналитически, служит контролем правильности решения.

7.20. Определить скорость, касательное и нормальное ускорения, радиус кривизны траектории точки для заданного момента времени.

( x и y – в см , t и t ₁ – в с).

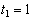
Найти: 1) вид траектории;

2) .

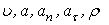
Указания. Задача — относится к кинематике точки и решается с помощью формул, по которым определяются скорость и ускорение точки в декартовых координатах (координатный способ задания движения точки), а также формул, по которым определяются скорость, касательное и нормальное ускорения точки при естественном способе задания ее движения. В задаче все искомые величины нужно определить только для момента времени t ₁ = 1 с .

1. Для определения уравнения траектории точки исключим из заданных уравнений движения время t :

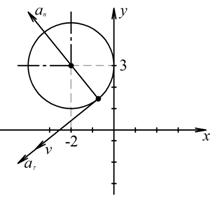
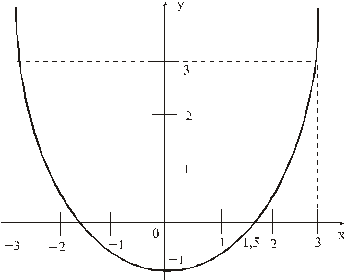
Отсюда окончательно находим уравнение траектории точки (параболы, см. рисунок):

2. Скорость точки найдем по ее проекциям на координатные оси:

V = 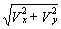и при t ₁ = 1 с,

3. Аналогично найдем ускорение точки:

а =

4. Касательное ускорение найдем, дифференцируя по времени равенство:

. (3)

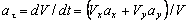
ч исловые значения всех величин, входящих в правую часть выражения (3), определены и даются равенствами (1) и (2).

Подставив в (3) эти числа, найдем сразу, что при t ₁ = 1 с

=7,49 см/с 2 .

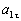
5. Нормальное ускорение точки:

a _n = .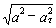

Подставляя сюда найденные числовые значения a ₁ и a _{1 τ} , получим, что при t ₁= 1 с

6. Радиус кривизны траектории ρ = V 2 / a _n .

Подставляя сюда числовые значения V ₁ и a _{1 n} , найдем, что при t ₁ = 1 с

Ответ: V ₁= 8 ,54 см/с, а ₁ =8 см/с 2 , 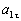=7,49 см/с 2 , a _{1 n} =2,81 см/с 2 , ρ₁ =25,95 см.

7.21. Точка движется по дуге окружности радиуса R =1 м по закону 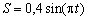( s – в метрах, t – в секундах), где s = AM (см. рисунок).

Найти: скорость и ускорение точки в момент времени t ₁ =1 с .

Определяем скорость точки:

V = ds / dt = .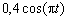

При t ₁ =1 с получим 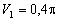= -1,26 м/ с .

Ускорение находим по его касательной и нормальной составляющим:

,

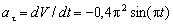
п ри t ₁ = 1 с получим , учтя, что R = 1 м

,

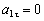
тогда ускорение точки при t ₁ =1 с будет:

=1,59 м/с 2 .

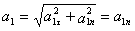
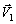
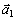
Изобразим на рисунке векторы , , учитывая знак V ₁ и считая положительным направление от А к М.

7.22. По заданным уравнениям движения точки М установить вид её траектории и для момента времени t = t ₁(с) найти положение точки на траектории, её скорость, полное, касательное и нормальное ускорения, а так же радиус кривизны траектории.

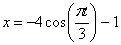
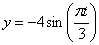
Дано: , , t ₁=1 сек ( x и y – в см , t и t ₁ – в с).

Найти: 1) вид траектории;

2) .

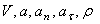
1) Найдём траекторию движения:

Для этого исключим параметр t .

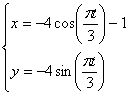
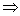
Возведём во вторую степень, получившиеся уравнения, а затем сложим, таким образом, исключится t . Получим:

Это окружность с центром в точке с координатами (-1;0) и радиусом

2) Найдём положение точки на траектории в момент времени t = t _1:

3) Определим скорость токи:

Для нахождения вектора полной скорости необходимо сложить 2 вектора:

Найдём модуль полной скорости:

для момента времени t ₁:

4) Определим ускорение точки:

для момента времени t ₁:

для момента времени t ₁:

Найдём полное ускорение:

Найдём модуль полного ускорения:

для момента времени t ₁:

Определим касательное ускорение :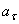

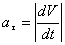
или,

для момента времени t :

Определим нормальное ускорение a_n :

для момента времени t ₁:

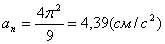
5) Из полученных результатов можно найти радиус кривизны траектории 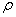, в момент времени t ₁:

Действительно, этот радиус совпадает с радиусом окружности (траектории).

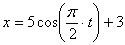
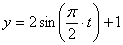
7.23. Точка М движется согласно уравнений ; ; ( x , y — в метрах, t — в секундах). Определить уравнение траектории точки, для момента времени t =1с, найти положение точки, а также скорость, полное, касательное, нормальное ускорения точки и радиус кривизны траектории.

1) Найдем уравнение траектории точки. Для определения уравнения траектории исключим из уравнений движения время . Из первого уравнения движения точки найдем

Из второго уравнения движения найдем

Возведя полученные значения ( правую и левую стороны уравнения ) в квадрат и складывая их находим:

.

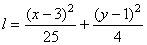
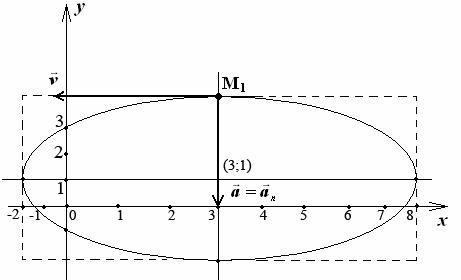
Следовательно, траекторией точки является эллипс с центром в точке с координатами (3;1).

Вид траектории показан на рисунке.

2) Найдем положение точки в момент времени t =1с

; .

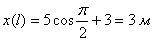
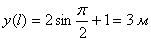
Положение точки М ₁ показано на рисунке.

3) Найдем скорость точки М

,

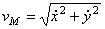
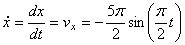
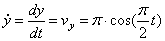
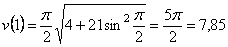
Где , или в момент времени t₁=1c

, или в момент времени t₁=1c

4) Найдём ускорение точки.

,

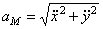
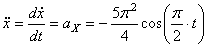
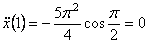
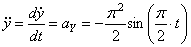
где , или ,

, или

5) Найдем касательное ускорение точки M,

6) Найдём нормальное ускорение точки M ,

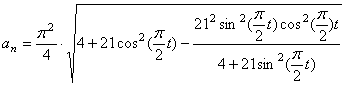
7) Найдем радиус кривизны траектории точки М,

,

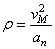
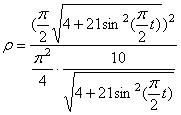
Направление векторов показано на рисунке.

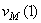
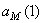
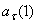
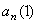
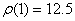
Ответ: =7.85м/ c ; = 4.93 м/ c 2 ; =0; = 4.93 м/ c 2 ; м

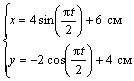
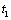
7.24. Пусть точка М движется в плоскости xOy в соответствии с уравнениями . Для момента времени = 0,5 с найти положение точки М на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.

Решение: Заданный закон движения точки в координатной форме можно рассматривать как параметрические уравнения траектории точки. Исключим время t из уравнений движения и получим уравнение траектории точки в виде:

.

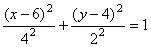
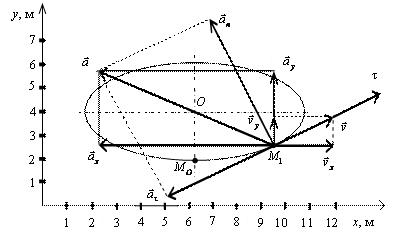
Таким образом, траекторией точки М является эллипс со смещенным центром, изображенный на рис. Отметим на траектории положение точки М ₁ ( x ₁, y ₁) в момент времени t ₁ = 0,5 c

;

.

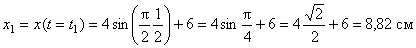
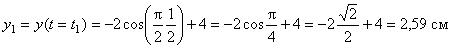
Вектор скорости точки представим в виде:

,

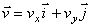
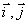
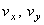
где – орты координатных осей О x и О y ; – проекции вектора скорости точки на координатные оси, которые равны 1-м производным от соответствующих координат по времени

В момент времени t ₁ = 0,5 c

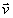
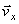
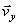
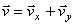
Вектор скорости точки строим по двум взаимно перпендикулярным проекциям и в соответствии с выбранным масштабом

.

Полученный вектор должен быть направлен по касательной к траектории точки в сторону движения. Модуль скорости точки определим по уже найденным проекциям

Вектор ускорения точки представим в виде:

,

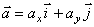
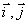
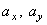
где – орты координатных осей О x и О y ; – проекции вектора скорости точки на координатные оси, которые равны 1-м производным от проекций вектора скорости или 2-м производным от соответствующих координат по времени:

В момент времени t ₁ = 0,5 c

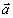
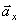
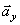
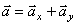
Вектор ускорения точки строим по двум взаимно перпендикулярным проекциям и в соответствии с выбранным масштабом

.

Полученный вектор ускорения точки в общем случае должен отклоняться от вектора скорости в сторону вогнутости траектории, а при движении по эллипсовидной траектории – проходить через центр эллипса. Модуль ускорения точки определим по уже найденным проекциям

Вектор полного ускорения точки можно также представить в виде геометрической суммы его проекций на оси естественной системы отсчета

,

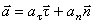
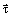
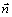
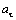
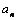
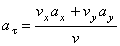
где и – единичные орты касательной и главной нормали; и – соответственно проекции вектора ускорения на касательную и главную нормаль. Касательную М ₁ t направляем по касательной к траектории в сторону движения точки движения, а главную нормаль М₁ n – перпендикулярно касательной в сторону вогнутости траектории. При вычислении касательного ускорения удобно воспользоваться формулой, устанавливающей связь между координатным и естественным способами задания движения точки

.

В момент времени t ₁ = 0,5 c

.

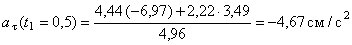
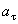
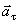
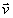
Значение касательного ускорения имеет отрицательный знак, следовательно, в данный момент времени движение точки замедленное и вектор касательного ускорения направлен в противоположную сторону направлению вектора скорости точки .

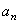
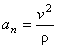
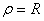
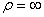
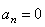
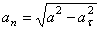
Нормальное ускорение вычислим по формуле , если известен радиус кривизны траектории. Например, если точка движется по окружности радиусом R, то в любой точке траектории . Если же траекторией движения точки является прямая, то , следовательно, . В данном случае радиус кривизны траектории заранее не известен, поэтому нормальное ускорение определяем по формуле:

.

В момент времени t ₁ = 0,5 c

.

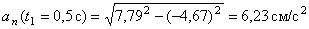
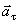
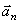
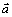
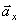
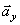
Построим векторы и в соответствии с уже выбранным масштабом, а затем сложим их геометрически. В результате получим тот же вектор полного ускорения точки , который ранее уже был получен геометрической суммой составляющих и . Этот факт служит контролем правильности решения.

Радиус кривизны траектории в рассматриваемой точке определим по формуле

.

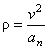
В момент времени t ₁ = 0,5 c

.

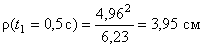
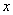
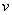
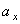
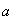
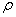
Ответ: =8,82 см; =2,59 см; =4,44 см/ c ; =2,22 см/ c ; =4,96 см/с; =6,97 см/с 2 ; =3,49 см/с 2 ; =7,79 см/с 2 ; =4,67 см/с 2 ; =6,23 см/с 2 ; =3,95 см (радиус кривизны траектории в точке ).

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

🎥 Видео

Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать

Кинематика точкиСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Движение точки тела. Способы описания движения | Физика 10 класс #2 | ИнфоурокСкачать

К1 Определение скорости и ускорения точки по заданным уравнениям ее движенияСкачать

ЕГЭ по математике. Профильный уровень. Задание 7. Закон движения. ПроизводнаяСкачать

Cложное движение точки. ТермехСкачать

кинематика точкиСкачать

Урок 87. Движение по наклонной плоскости (ч.1)Скачать

Кинематика точки. Три способа задания движения. Скорость, ускорениеСкачать

Кинематика точки в плоскости. ТермехСкачать

Как решать задачи по кинематике.Скачать

Физика - уравнения равноускоренного движенияСкачать

Решение графических задач на равномерное движениеСкачать

Сложное движение точки. Задача 1Скачать

Задача 1.1. КИНЕМАТИКА | Учимся решать задачи по физике с нуляСкачать

ЗАДАЧИ НА НАКЛОННУЮ ПЛОСКОСТЬ - не ГРОБ! КАК ТАКИЕ РЕШАТЬ?Скачать

Видеоурок "Уравнение плоскости по трем точкам"Скачать