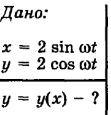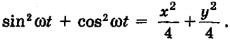Про уравнения - легко » Статьи

Точка движется в плоскости xoy согласно уравнениям

Обновлено
Нужно решить задачи К-1 и Д 2

Точка движется в плоскости xoy согласно уравнениям

Нужно решить задачи К-1 и Д 2

4.1.1. К -1. Определение скорости и ускорения

точки по заданным уравнениям её движения

Определить: уравнение траектории точки; для момента времени t1=1с найти скорость и ускорение точки, а также её касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.

Указания: задача К1 относится к кинематике точки; скорость и ускорение точки в декартовых координатах определяются по формулам координатного способа задания движения точки, а касательное и нормальное ускорения точки — по формулам естественного способа задания её движения.

По предпоследней цифре шифра зачетной книжки выбирается уравнение, задающее изменении координаты X(t), а по последней – Y(t).

В задаче все искомые величины следует определить для момента времени t1=1с.

Дано: уравнения движения точки в плоскости XOY:

Определить: уравнение траектории точки; для момента времени t1=1с найти скорость и ускорение точки, а также её касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.

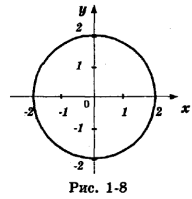
1. Для определения уравнения траектории точки исключим из данных уравнений движения параметр t:

Точка движется в плоскости xoy согласно уравнениямТочка движется в плоскости xoy согласно уравнениямТочка движется в плоскости xoy согласно уравнениям

Точка движется в плоскости xoy согласно уравнениям— уравнение траектории точки – эллипс с полуосями 12 см и 4 см (рис. К -1).Точка движется в плоскости xoy согласно уравнениям

2. Определим положение точки на траектории в момент времени t1=1с :

Точка движется в плоскости xoy согласно уравнениям
3. Скорость точки находим по её проекциям на координатные оси:

Точка движется в плоскости xoy согласно уравнениям

Точка движется в плоскости xoy согласно уравнениям

Точка движется в плоскости xoy согласно уравнениям, при t1=1с Точка движется в плоскости xoy согласно уравнениям

2. Аналогично найдём ускорение точки при t1=1с :

Точка движется в плоскости xoy согласно уравнениям

Точка движется в плоскости xoy согласно уравнениям

Точка движется в плоскости xoy согласно уравнениям, при t1=1с Точка движется в плоскости xoy согласно уравнениям

5. Находим касательное ускорение точки, зная численные значения всех величин, входящих в правую часть выражения:

Точка движется в плоскости xoy согласно уравнениямпри t1=1с Точка движется в плоскости xoy согласно уравнениям

6. Нормальное ускорение точки определяем по формуле , подставляя известные численные значения. При t1=1с получим Точка движется в плоскости xoy согласно уравнениям

5.3.3. Д -2. Применение теоремы об изменении кинетической энергии

к изучению движения механической системы

два вариант 2 и 3

Дано. Механическая система состоит из катков 1 и 2 (или катка и подвижного блока), ступенчатого шкива 3 с радиусами ступеней R3= 0,3 м, r3 = 0,1 м и радиусом инерции относительно оси вращения ρ3 = 0,2 м, блока 4 радиуса R4= 0,2 м и грузов 5 и 6 (рис. Д 2.0 – Д 2.9, табл. Д-2); тела 1 и 2 считать сплошными однородными цилиндрами, а массу блока 4 – равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f=0,1. Тела системы соединены друг с

другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с.

Под действием силы F=f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сил сопротивления (от трения в подшипниках).

Все катки катятся по плоскостям без скольжения.

Если по заданию массы грузов 5 и 6 или массы катков 1 (рис. Д 2.0-2.4) и 2 (рис. Д 2.5-2.9) равны нулю, то на чертеже их можно не изображать.

Определить: значение искомой величины в тот момент времени, когда перемещение s станет равным s1= 0,2 м. Искомая величина указана в столбце «Найти» таблицы Д 2, где обозначено: ω3 – угловая скорость тела 3; ε4 – угловое ускорение тела 4; v5 – скорость тела 5; ас2- ускорение центра масс тела 2 и т. п.

Указания. При решении задачи учесть, что кинетическая энергия системы равна сумме кинетических энергий всех входящих в систему тел; эту энергию следует выразить через ту скорость (линейную или угловую), которую в задаче надо определить. При вычислении энергии для установления зависимости между скоростями точек тела, движущегося плоскопараллельно, или между его угловой скоростью и скоростью центра масс воспользоваться мгновенным центром скоростей. При вычислении работы необходимо все перемещения выразить через заданное перемещение s1, учитывая при этом, что зависимость между перемещениями здесь будет такой же, как между соответствующими скоростями.

Содержание
  1. Материальная точка движется в плоскости XOY, и при этом ее координаты
  2. Пример решения задачи №10.
  3. Точка движется в плоскости xoy согласно уравнениям
  4. Как написать хороший ответ?
  5. 🔥 Видео

Видео:Движение точки тела. Способы описания движения | Физика 10 класс #2 | ИнфоурокСкачать

Движение точки тела. Способы описания движения | Физика 10 класс #2 | Инфоурок

Материальная точка движется в плоскости XOY, и при этом ее координаты

Точка движется в плоскости xoy согласно уравнениям

Пример решения задачи №10.

Материальная точка движется в плоскости XOY, и при этом ее координаты изменяются с течением времени по закону 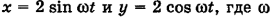Точка движется в плоскости xoy согласно уравнениям— константа. Какова траектория точки?

Точка движется в плоскости xoy согласно уравнениям

Решение:

Исключим время t из уравнений:

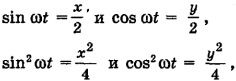
Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям

Точка движется в плоскости xoy согласно уравнениям

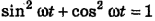
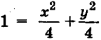
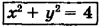
Так как Точка движется в плоскости xoy согласно уравнениям,
то Точка движется в плоскости xoy согласно уравнениям, или Точка движется в плоскости xoy согласно уравнениям— окружность.

Ответ: 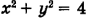Точка движется в плоскости xoy согласно уравнениям— окружность с радиусом R = 2 м (рис. 1-8).

Эта задача взята со страницы подробного решения задач по физике, там теория и задачи по всем темам физики, можете посмотреть:

Возможно вам будут полезны ещё вот эти задачи:

Точка движется в плоскости xoy согласно уравнениям

Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям Точка движется в плоскости xoy согласно уравнениям

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Видео:Кинематика точки в плоскости. ТермехСкачать

Кинематика точки в плоскости. Термех

Точка движется в плоскости xoy согласно уравнениям

Вопрос по физике:

Материальная точка движется в плоскости XOY. Уравнение движения имеют вид: x=3t+5 и y=4t-3. С какой скоростью движется точка?

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 2

Из уравнений движения Vx=3 Vy=4 V=sqrt(Vx^2+Vy^2)=sqrt(9+16)=5 м/с

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

  • Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
  • Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
  • Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

  • Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
  • Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
  • Использовать мат — это неуважительно по отношению к пользователям;
  • Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Физика.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Физика — область естествознания: естественная наука о простейших и вместе с тем наиболее общих законах природы, о материи, её структуре и движении.

🔥 Видео

Траектория и уравнения движения точки. Задача 1Скачать

Траектория и уравнения движения точки. Задача 1

Математика без Ху!ни. Уравнение плоскости.Скачать

Математика без Ху!ни. Уравнение плоскости.

ЕГЭ по математике. Профильный уровень. Задание 7. Закон движения. ПроизводнаяСкачать

ЕГЭ по математике. Профильный уровень. Задание 7. Закон движения. Производная

4.11Скачать

4.11

К1 Определение скорости и ускорения точки по заданным уравнениям ее движенияСкачать

К1 Определение скорости и ускорения точки по заданным уравнениям ее движения

Кинематика точки Задание К1Скачать

Кинематика точки Задание К1

Физика 10 класс (Урок№2 - Равномерное прямолинейное движение материальной точки.)Скачать

Физика 10 класс (Урок№2 - Равномерное прямолинейное движение материальной точки.)

ДВИЖЕНИЕ ПО НАКЛОННОЙ ПЛОСКОСТИ | механика 10 классСкачать

ДВИЖЕНИЕ ПО НАКЛОННОЙ ПЛОСКОСТИ | механика 10 класс

Дифференциальное уравнение движения материальной точки.Скачать

Дифференциальное уравнение движения материальной точки.

13.1. Определение сил по заданному движениюСкачать

13.1. Определение сил по заданному движению

кинематика точкиСкачать

кинематика точки

Материальная точка движется по закону. Физический смысл производной. 18 вариант Ященко Задание 7Скачать

Материальная точка движется по закону. Физический смысл производной. 18 вариант Ященко Задание 7

3. Частные случаи общего уравнения плоскости Неполные уравнения плоскостиСкачать

3. Частные случаи общего уравнения плоскости Неполные уравнения плоскости

Движение материальной точки по окружности | Физика ЕГЭ, ЦТСкачать

Движение материальной точки по окружности | Физика ЕГЭ, ЦТ

Решение графических задач на равномерное движениеСкачать

Решение графических задач на равномерное движение

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.

2. Уравнение плоскости примеры решения задач #1Скачать

2. Уравнение плоскости примеры решения задач #1

Урок 9. Проекции вектора на координатные осиСкачать

Урок 9. Проекции вектора на координатные оси
Поделиться или сохранить к себе: