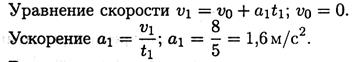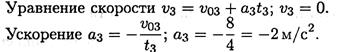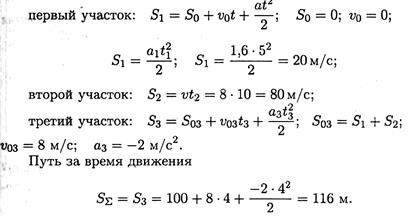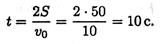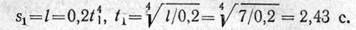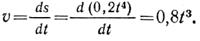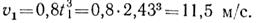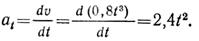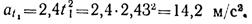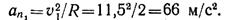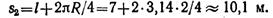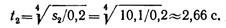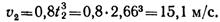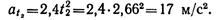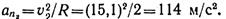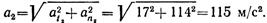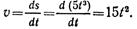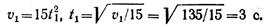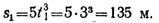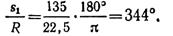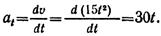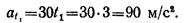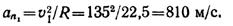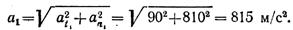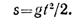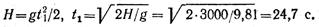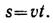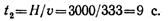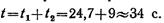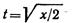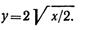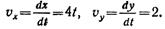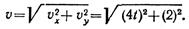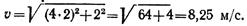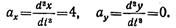Пример 1. По заданному закону движения S =10 + 20t — 5t 2 ([S] = м; [t] = с) определить вид движения, начальную скорость и касательное ускорение точки, время до остановки.
(Рекомендуется обойтись без расчетов, использовать метод сравнения заданного уравнения с уравнениями различных видов движений в общем виде.)
Решение
1. Вид движения: равнопеременное
2. При сравнении уравнений очевидно, что
- начальный путь, пройденный до начала отсчета – 10 м;
- начальная скорость 20 м/с;
- постоянное касательное ускорение at/2 = 5 м/с ; at= — 10 м/с .
- ускорение отрицательное, следовательно, движение замедленное (равнозамедленное), ускорение направлено в сторону, противоположную направлению скорости движения.
3. Можно определить время, при котором скорость точки будет равна нулю:
v = S’ = 20 — 2 • 5t; v = 20 – 10t = 0; t = 20/10 = 2 c.
Примечание. Если при равнопеременном движении скорость растет, значит, ускорение — положительная величина, график пути — вогнутая парабола. При торможении скорость падает, ускорение (замедление) — отрицательная величина, график пути — выпуклая парабола (рис. 10.4).
Пример 2. Точка движется по желобу из точки А в точку D (рис. 10.5).
Как изменятся касательное и нормальное ускорения при прохождении точки через В и С?
Скорость движения считать постоянной. Радиус участка АВ = 10 м, радиус участка ВС= 5 м.
Решение
1. Рассмотрим участок АВ. Касательное ускорение равно нулю (v = const).
Нормальное ускорение (ап = v 2 /r) при переходе через точку В увеличивается в 2 раза, оно меняет направление, т. к. центр дуги АВ не совпадает с центром дуги ВС.
2. На участке ВС:
— касательное ускорение равно нулю: at = 0;
— нормальное ускорение при переходе через точку С меняется: до точки С движение вращательное, после точки С движение становится прямолинейным, нормальное напряжение на прямолинейном участке равно нулю.
3. На участке CD полное ускорение равно нулю.
Пример 3. По заданному графику скорости найти путь, пройденный за время движения (рис. 10.6).
Решение
1. По графику следует рассмотреть три участка движения. Первый участок — разгон из состояния покоя (равноускоренное движение).
Второй участок — равномерное движение: v = 8 м/с; a2 = 0.
Третий участок — торможение до остановки (равнозамедленное движение).
2. Путь, пройденный за время движения, будет равен:
Пример 4. Тело, имевшее начальную скорость 36 км/ч, прошло 50 м до остановки. Считая движение равнозамедленным, определить время торможения.
Решение
1. Записываем уравнение скорости для равнозамедленного движения:
Определяем начальную скорость в м/с: vо = 36*1000/3600 = 10 м/с.
Выразим ускорение (замедление) из уравнения скорости: a = — v0/t
2. Записываем уравнение пути: S = vot/2 + at 2 /2. После подстановки получим: S = vot/2
3. Определяем время до полной остановки (время торможения):
Пример 5. Точка движется прямолинейно согласно уравнению s = 20t – 5t 2 (s — м, t — с). Построить графики расстояний, скорости и ускорения для первых 4 с движения. Определить путь, пройденный точкой за 4 с, и описать движение точки.
Решение
1. Точка движется прямолинейно по уравнению s = 20t – 5t 2 следовательно, скорость точки u = ds/d/t = 20 — 10t и ускорение a = at = dv/dt = —10 м/с 2 . Значит, движение точки равнопеременное (a = at = —10 м/c 2 = const) с начальной скоростью v0 = 20 м/с.
2. Составим зависимость числовых значений s и v для первых 4 с движения
3. По приведенным числовым значениям построим графики расстояний (рис. а), скорости (рис. б) и ускорения (рис. в), выбрав масштабы для изображения по осям ординат расстояний s, скорости v и ускорения а, а также одинаковый для всех графиков масштаб времени по оси абсцисс. Например, если расстояние s = 5 м изображать на графике длиной отрезка ls = 10 мм, то 5м = μs*10мм, где коэффициент пропорциональности μs и есть масштаб по оси Os : μs = 5/10 = 0,5 м/мм (0,5 м в 1 мм); если модуль скорости v = 10 м/с изображать на графике длиной lv =10 мм, то 10 м/c = μv * 10 мм и масштаб по оси Ov μv = 1 м/(с-мм) (1 м/с в 1 мм); если модуль ускорения а = 10 м/с 2 изображать отрезком la = 10 мм, то, аналогично предыдущему, масштаб по оси Оа μa = 1 м/(с 2 -мм) (1 м/с 2 в 1 мм); и наконец, изображая промежуток времени Δt = 1 с отрезком μt = 10 мм, получим на всех графиках масштаб по осям Ot μt = 0,1 с/мм (0,1 с в 1 мм).
4. Из рассмотрения графиков следует, что в течение времени от 0 до 2 с точка движется равнозамедленно (скорость v и ускорение в течение этого промежутка времени имеют разные знаки, значит, их векторы направлены в противоположные стороны); в период времени от 2 до 4 с точка движется равноускоренно (скорость v и ускорение имеют одинаковые знаки, т. е. их векторы направлены в одну сторону).
За 4 с точка прошла путь so_4 = 40 м. Начав движение со скоростью v0 = 20 м/с, точка по прямой прошла 20 м, а затем вернулась в исходное положение, имея ту же скорость, но направленную в противоположную сторону.
Если условно принять ускорение свободного падения g = 10 мс 2 и пренебречь сопротивлением воздуха, то можно сказать, что графики описывают движение точки, брошенной вертикально вверх со скоростью а0 = 20 м/с.
Пример 6. Точка движется по траектории, изображенной на рис. 1.44, а, согласно уравнению s = 0,2t 4 (s — в метрах, t — в секундах). Определить скорость и ускорение точки в положениях 1 и 2.
Решение
Время, необходимое для перемещения точки из положения 0 (начала отсчета) в положение 1, определим из уравнения движения, подставив частные значения расстояния и времени:
Уравнение изменения скорости
Скорость точки в положении 1
Уравнение изменения касательного ускорения
Касательное ускорение точки в положении 1
Нормальное ускорение точки на прямолинейном участке траектории равно нулю. Скорость и ускорение точки в конце этого участка траектории показаны на рис.1.44, б.
Определим скорость и ускорение точки в начале криволинейного участка траектории. Очевидно, что v1 = 11,5 м/с, аt1 = 14,2 м/с 2 .
Нормальное ускорение точки в начале криволинейного участка
Скорость и ускорение в начале криволинейного участка показаны на рис. 1.44, в (векторы at1 и aa1 изображены без соблюдения масштаба).
Положение 2 движущейся точки определяется пройденным путем, состоящим из прямолинейного участка 0 — 1 и дуги окружности 1 — 2, соответствующей центральному углу 90°:
Время, необходимое для перемещения точки из положения 0 в положение2,
Скорость точки в положении 2
Касательное ускорение точки в положении 2
Нормальное ускорение точки в положении 2
Ускорение точки в положении 2
Скорость и ускорения точки в положении 2 показаны на рис. 1.44, в (векторы at„ и аПг изображены без соблюдения масштаба).
Пример 7. Точка движется по заданной траектории (рис. 1.45, а) согласно уравнению s = 5t 3 (s — в метрах, t — в секундах). Определить ускорение точки и угол α между ускорением и скоростью в момент t1, когда скорость точки v1 = 135 м/с.
Решение
Уравнение изменения скорости
Время t1 определим из уравнения изменения скорости, подставив частные значения скорости и времени:
Определим положение точки на траектории в момент 3 с:
Дуга окружности длиной 135 м соответствует центральному углу
Уравнение изменения касательного ускорения
Касательное ускорение точки в момент tt
Нормальное ускорение точки в момент tt
Ускорение точки в момент tx
Скорость и ускорение точки в момент времени t1 показаны на рис. 1.45, б.
Как видно из рис. 1.45, б
Пример 8. В шахту глубиной H = 3000 м с поверхности земли без начальной скорости брошен предмет. Определить, через сколько секунд звук, возникающий в момент удара предмета о дно шахты, достигнет поверхности земли. Скорость звука 333 м/с.
Решение
Уравнение движения свободно падающего тела
Время, необходимое для перемещения предмета от поверхности земли до дна шахты, определим из уравнения движения:
Звук распространялся с постоянной скоростью 333 м/с. Уравнение распространения звука
Время достижения звуком поверхности земли
Тогда время с момента начала движения предмета до момента достижения звуком поверхности земли
Пример 9. По заданным уравнениям движения точки x = 2t 2 , y = 2t (x и у — в метрах, t — в секундах) найти уравнение траектории, а также скорость и ускорение точки в момент времени t = 2 с.
Решение
Для определения траектории точки нужно из уравнений движения исключить параметр t — время.
Выразим t через х из первого уравнения:
и подставим это значение во второе уравнение:
Траекторией точки является парабола, симметричная относительно оси х.
Чтобы найти скорость точки, нужно определить ее составляющие по координатным осям
Находим скорость точки
При t = 2 с получаем
Находим составляющие ускорения точки
Контрольные вопросы и задания
1. Запишите формулу ускорения при прямолинейном движении.
2. Запишите формулу ускорения (полного) при криволинейном движении.
3. 
Тело скатывается по желобу (рис. 10.7). Какие параметры движения меняются при переходе через точку В и почему?
4. Параметры движения не меняются.
4. По заданному уравнению движения точки S = 25 + 1,5t + 6t 2 определите вид движения и без расчетов, используя законы движения точки, ответьте, чему равны начальная скорость и ускорение.
5. По заданному уравнению движения точки S = 22t — 4t 2 постройте графики скорости и касательного ускорения.
6. По графику скоростей точки определите путь, пройденный за время движения (рис. 10.8).
7. Точка движется по дуге. Охарактеризуй движение точки (рис. 10.9).
 |
8. Ответьте на вопросы тестового задания.
Темы 1.7, 1.8. Кинематика. Кинематика точки
 |
.
ЛЕКЦИЯ 11
Дата добавления: 2017-09-01 ; просмотров: 10616 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:ЕГЭ Задание 7. Материальная точка движется по законуСкачать
Алгебра и начала математического анализа. 11 класс
Конспект урока
Алгебра и начала математического анализа, 11 класс
Урок №19. Решение задач с помощью производной.
Перечень вопросов, рассматриваемых в теме
- механический смысл первой производной;
- механический смысл второй производных;
- скорость и ускорение.
Глоссарий по теме
Производная y’(x) функции y=f(x) – это мгновенная скорость изменения этой функции. В частности, если зависимость между пройденным путём S и временем t при прямолинейном неравномерном движении выражается уравнением S=f(t), то для нахождения мгновенной скорости точки в какой-нибудь определённый момент времени t нужно найти производную S’=f’(x) и подставить в неё соответствующее значение t, то есть v(t)=S’(t).
Производная от данной функции называется первой производной или производной первого порядка. Но производная функции также является функцией, и если она дифференцируема, то от неё, в свою очередь, можно найти производную.
Производная от производной называется второй производной или производной второго порядка и обозначается f
или 
Производная от второй производной называется производной третьего порядка и обозначается 
или f»’(x). Производную n-го порядка обозначают f (n) (x) или y (n) .
Если первая производная функции – это мгновенная скорость изменения любого процесса, заданного функцией, то вторая производная – это скорость изменения скорости, то есть ускорение, то есть 
Первая производная – это скорость изменения процесса, вторая производная – ускорение. (v= S’; a=v’)
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Давайте вспомним механический смысл производной:
Производная y’(x) функции y=f(x) – это мгновенная скорость изменения этой функции. В частности, если зависимость между пройденным путём S и временем t при прямолинейном неравномерном движении выражается уравнением S=f(t), то для нахождения мгновенной скорости точки в какой-нибудь определённый момент времени t нужно найти производную S’=f’(x) и подставить в неё соответствующее значение t, то есть v(t)=S'(t).
Пример 1. Точка движется прямолинейно по закону 
(S выражается в метрах, t – в секундах). Найти скорость движения через 3 секунды после начала движения.
скорость прямолинейного движения равна производной пути по времени, то есть 
.
Подставив в уравнение скорости t=3 с, получим v(3)=32+4∙3-1= 20 (м/с).
Пример 2. Маховик, задерживаемый тормозом, поворачивается за t с на угол
Найдите:
а) угловую скорость вращения маховика в момент t = 6 с;
б) в какой момент времени маховик остановится?
Решение: а) Угловая скорость вращения маховика определяется по формуле ω=φ’. Тогда ω=(4t-0,2t 2 )=4-0,4t.
Подставляя t = 6 с, получим ω=4-0,4∙6=1,6 (рад/с).
б) В тот момент, когда маховик остановится, его скорость будет равна нулю (ω=0) . Поэтому 4-0,4t=0.. Отсюда t=10 c.
Ответ: угловая скорость маховика равна (рад/с); t=10 c.
Пример 3. Тело массой 6 кг движется прямолинейно по закону S=3t 2 +2t-5. Найти кинетическую энергию тела 
через 3 с после начала движения.
Решение: найдём скорость движения тела в любой момент времени t.
Вычислим скорость тела в момент времени t=3. v(3)=6∙3+2=20 (м/с)..
Определим кинетическую энергию тела в момент времени t=3.
Производная второго порядка. Производная n-го порядка.
Производная от данной функции называется первой производной или производной первого порядка. Но производная функции также является функцией, и если она дифференцируема, то от неё, в свою очередь, можно найти производную.
Производная от производной называется второй производной или производной второго порядка и обозначается 
.
Производная от второй производной называется производной третьего порядка и обозначается y»’ или f»'(x) Производную n-го порядка обозначают f (n) (x) или y (n) .
Примеры. Найдем производные четвёртого порядка для заданных функций:
f'(x)=cos 2x∙(2x)’= 2cos 2x
f 
(x)=-2sin2x∙(2x)’=-4sin 2x
f»'(x)= -4 cos 2x∙(2x)= -8 cos 2x
f (4) (x)= 8 sin2x∙(2x)’= 16 sin 2x
f 
(x)= 9∙ 2 3x ∙ln 2 2
f»'(x)= 27∙ 2 3x ∙ln 3 2
f (4) (x)= 81∙ 2 3x ∙ln 4 2
Механический смысл второй производной.
Если первая производная функции – это мгновенная скорость изменения любого процесса, заданного функцией, то вторая производная – это скорость изменения скорости, то есть ускорение, то есть 
Итак, первая производная – это скорость изменения процесса, вторая производная – ускорение. (v= S’; a=v’)
Пример 4. Точка движется прямолинейно по закону S(t)= 3t 2 -3t+8. Найти скорость и ускорение точки в момент t=4 c.
найдём скорость точки в любой момент времени t.
Вычислим скорость в момент времени t=4 c.
Найдём ускорение точки в любой момент времени t.
a= v’= (6t-3)’=6 и a(4)= 6 (м/с 2 ) , то есть ускорение в этом случае является величиной постоянной.
Ответ: v=21(м/с); a= v’= 6 (м/с 2 ).
Пример 5. Тело массой 3 кг движется прямолинейно по закону S(t)=t 3 -3t 2 +5. Найти силу, действующую на тело в момент времени t=4 c.
Решение: сила, действующая на тело, находится по формуле F=ma.
Найдём скорость движения точки в любой момент времени t.
v=S’=(t 3 -3t 2 +5)’=3t 2 -6t.
Тогда v(4)=3∙4 2 -6∙4=24 (м/с).
Найдём ускорение: a(t)=v’=(3t 2 -6t)’=6t-6.
Тогда a(4)= 6∙4-6= 18 (м/с 2 ).
Разбор решения заданий тренировочного модуля
№ 1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте
Напишите производную третьего порядка для функции:
f(x)= 3cos4x-5x 3 +3x 2 -8
Решим данную задачу:
f’’’(x)=( 3cos4x-5x 3 +3x 2 -8)’’’=(((3cos4x-5x 3 +3x 2 -8)’)’)’=((-12sin4x-15x 2 +6x)’)’=(-48cos4x-30x)’=192sin4x-30.
№ 2. Тип задания: выделение цветом
Точка движется прямолинейно по закону S(t)= 3t 2 +2t-7. Найти скорость и ускорение точки в момент t=6 c.
- v=38 м/с; a=6 м/с 2
- v=38 м/с; a=5 м/с 2
- v=32 м/с; a=6 м/с 2
- v=32 м/с; a=5 м/с 2
Решим данную задачу:
Воспользуемся механическим смыслом второй производной:
v= S’(t)=( 3t 2 +2t-7)’=6t+2.
Вычислим скорость в момент времени t=6 c.
Найдём ускорение точки в любой момент времени t.
a= v’= (6t+2)’=6 и a(6)= 6 (м/с 2 ) , то есть ускорение в этом случае является величиной постоянной.
Ответ: v=38(м/с); a= v’= 6 (м/с 2 ).
- v=38 м/с; a=6 м/с 2
- v=38 м/с; a=5 м/с 2
- v=32 м/с; a=6 м/с 2
- v=32 м/с; a=5 м/с 2
Видео:ЕГЭ по математике. Профильный уровень. Задание 7. Закон движения. ПроизводнаяСкачать
Комплект контрольно – оценочных средств по учебной дисциплине ОП.02Техническая механика (стр. 3 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 |
мм2; 
мм
мм2; 
мм
мм2; 
мм
мм2; 
мм
мм3
мм3
мм3
мм3
мм3
4. Определим статический момент и площадь всего сечения:
мм3
мм2
5. Определим положение центра тяжести сечения:
мм
6. Наносим на ось у центр тяжести всего сечения
Ответ: центр тяжести С имеет координаты С (0; 28,6)
6. Критерии оценки знаний.
Основные критерии оценки
Работа выполнена правильно, без ошибок, оформлена согласно методическим указаниям.
Работа выполнена правильно, но в оформлении допущены небольшие погрешности.
В работе допущены ошибки, оформление небрежное, есть погрешности.
7. Тесты на проверку знаний по теме «Центр тяжести»
Можно ли считать силу тяжести тела равнодействующей системы параллельных сил?
Так считать нельзя
Сила тяжести тела не имеет отношения к системе параллельных сил
Может ли центр тяжести располагаться вне самого тела?
Да, может располагаться вне тела
Нет, не может быть вне тела
В каких единицах измеряется статический момент сечения?
Единица длины в третьей степени
Единица длины во второй степени
Единица длины в первой степени
Где располагается центр тяжести тела, имеющего ось симметрии?
На оси симметрии
Вне оси симметрии, в любой точке тела
Вне самого тела
В каком отношении делит центр тяжести прямоугольного треугольника противоположные катеты
В отношении один к трем
В отношении один к двум
Время выполнения 5 – 10 минут.
«Техническая механика», Москва «Высшая школа», 2003
Тема 4: «Кинематика точки. Построение графиков пути,
скорости и ускорения точки».
1. Задание №4. Построить графики пути, скорости и ускорения точки, движущейся прямолинейно согласно закону для первых пяти секунд движения. Данные из своего варианта взять из таблицы.
Уравнение движения точки
Уравнение движения точки
2.1 Проверить степень усвоения студентами темы «Кинематика точки. Построение графиков пути, скорости ускорения».
2.2 Научиться строить кинематические графики.
3. Повторение теоретического материала.
3.1 Что такое «закон движения точки» и какими способами он задается?
3.2 Что характеризует нормальное и касательное ускорение и как их можно определить?
3.3 Как определить числовое значение и направление скорости точки в данный момент?
3.4 Что называется равнопеременным движением и какие виды его существуют?
3.5 Что такое средняя скорость движения точки и как она определяется?
4. Методические рекомендации к выполнению задания №4.
4.1 Продифференцировать заданное уравнение движения, чтобы получить уравнение скорости
4.2 Продифференцировать уравнение скорости, чтобы получить значение касательного ускорения:
4.3 Составить свободную таблицу числовых значений S, υ, at при значениях времени t от 0 до 4 с.
4.4 Построить графики S, υ, at выбрав масштабы для изображения по осям ординат, а также одинаковой для всех графиков масштаб времени по оси абсцисс.
5. Пример выполнения задания №4.
Точка движется прямолинейно согласно уравнению S = 17t – 2t2 м. Построить графики расстояний, скорости и ускорения для первых пяти секунд движения.
5.1 Определим закон изменения скорости движения точки.
5.2 Определим ускорение точки
Поскольку ускорение постоянное, т. е. at = const, следовательно движение точки является равнопеременным (равнозамедленным).
5.3 Составим свободную таблицу значений S, υ, at, для первых пяти секунд движения
📸 Видео
Материальная точка движется прямолинейно по закону x(t) В какой момент времени ее скорость = 2 м/с?Скачать
Прямолинейное равноускоренное движение. Ускорение | Физика 9 класс #5 | ИнфоурокСкачать
Урок 18 (осн). Координаты тела. График движения. График скоростиСкачать
Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать
Урок 12. Равномерное прямолинейное движениеСкачать
Задачи на движение. Учимся решать задачи на движение. Способы решения задач на движение.Скачать
Скорость и перемещение при прямолинейном равноускоренном движении. 9 класс.Скачать
Графики зависимости пути и скорости от времениСкачать
Равномерное прямолинейное движение - физика 9Скачать
Урок 47. Неравномерное движение по окружности. Тангенциальное ускорениеСкачать
Кинематика. Закон движения. Урок 3Скачать
УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать
Вариант #20 из задач ФИПИ - Уровень Сложности ЕГЭ 2024| Математика Профиль| Оформление на 100 БалловСкачать
Материальная точка движется по закону. Физический смысл производной. 18 вариант Ященко Задание 7Скачать
Решение графических задач на равномерное движениеСкачать
Физика - перемещение, скорость и ускорение. Графики движения.Скачать
Уравнение равномерного прямолинейного движения | Физика 10 класс #3 | ИнфоурокСкачать
Урок 16 (осн) Средняя скорость. Вычисление пути и времени движенияСкачать
