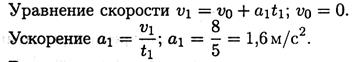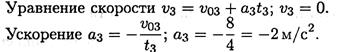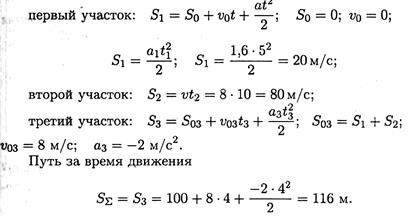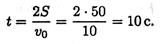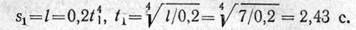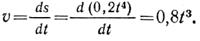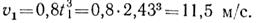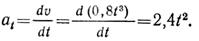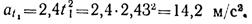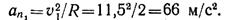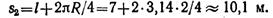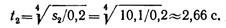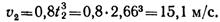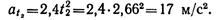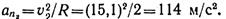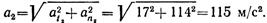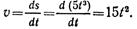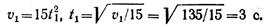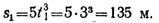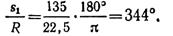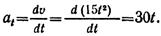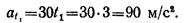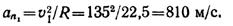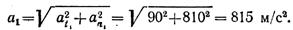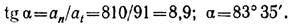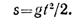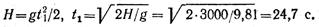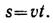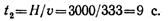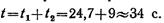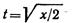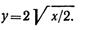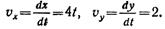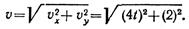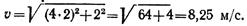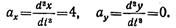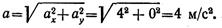Точка движется по заданной траектории согласно уравнению s kt 3 (3 видео)

Содержание

Примеры решения задач
Точка движется по окружности радиусом R = 2 см согласно уравнению S = Ct3, где C = 0,1 см/с3.
Описание и исходные данные задания, 50% решения + фотография:
Точка движется по заданной траектории согласно уравнению s kt 3
💡 Видео

Видео:Траектория и уравнения движения точки. Задача 1Скачать

Примеры решения задач

Пример 1. По заданному закону движения S =10 + 20t — 5t 2 ([S] = м; [t] = с) определить вид движения, начальную скорость и касательное ускорение точки, время до остановки.

(Рекомендуется обойтись без расчетов, использовать метод сравнения заданного уравнения с уравнениями различных видов движений в общем виде.)

Решение

1. Вид движения: равнопеременное

2. При сравнении уравнений очевидно, что

начальный путь, пройденный до начала отсчета – 10 м;
начальная скорость 20 м/с;
постоянное касательное ускорение a_t/2 = 5 м/с ; a_t= — 10 м/с .
ускорение отрицательное, следовательно, движение замедленное (равнозамедленное), ускорение направлено в сторону, противоположную направлению скорости движения.

3. Можно определить время, при котором скорость точки будет равна нулю:

v = S’ = 20 — 2 • 5t; v = 20 – 10t = 0; t = 20/10 = 2 c.

Примечание. Если при равнопеременном движении скорость растет, значит, ускорение — положительная величина, график пути — вогнутая парабола. При торможении скорость падает, ускорение (замедление) — отрицательная величина, график пути — выпуклая парабола (рис. 10.4).

Пример 2. Точка движется по желобу из точки А в точку D (рис. 10.5).

Как изменятся касательное и нормальное ускорения при прохождении точки через В и С?

Скорость движения считать постоянной. Радиус участка АВ = 10 м, радиус участка ВС= 5 м.

Решение

1. Рассмотрим участок АВ. Касательное ускорение равно нулю (v = const).

Нормальное ускорение (а_п = v 2 /r) при переходе через точку В увеличивается в 2 раза, оно меняет направление, т. к. центр дуги АВ не совпадает с центром дуги ВС.

2. На участке ВС:

— касательное ускорение равно нулю: a_t = 0;

— нормальное ускорение при переходе через точку С меняется: до точки С движение вращательное, после точки С движение становится прямолинейным, нормальное напряжение на прямолинейном участке равно нулю.

3. На участке CD полное ускорение равно нулю.

Пример 3. По заданному графику скорости найти путь, пройденный за время движения (рис. 10.6).

Решение

1. По графику следует рассмотреть три участка движения. Первый участок — разгон из состояния покоя (равноускоренное движение).

Второй участок — равномерное движение: v = 8 м/с; a₂ = 0.

Третий участок — торможение до остановки (равнозамедленное движение).

2. Путь, пройденный за время движения, будет равен:

Пример 4. Тело, имевшее начальную скорость 36 км/ч, прошло 50 м до остановки. Считая движение равнозамедленным, определить время торможения.

Решение

1. Записываем уравнение скорости для равнозамедленного движения:

Определяем начальную скорость в м/с: v_о = 36*1000/3600 = 10 м/с.

Выразим ускорение (замедление) из уравнения скорости: a = — v₀/t

2. Записываем уравнение пути: S = v_ot/2 + at 2 /2. После подстановки получим: S = v_ot/2

3. Определяем время до полной остановки (время торможения):

Пример 5. Точка движется прямолинейно согласно уравнению s = 20t – 5t 2 (s — м, t — с). Построить графики расстояний, скорости и ускорения для первых 4 с движения. Определить путь, пройденный точкой за 4 с, и описать движение точки.

Решение

1. Точка движется прямолинейно по уравнению s = 20t – 5t 2 следовательно, скорость точки u = ds/d/t = 20 — 10t и ускорение a = a_t = dv/dt = —10 м/с 2 . Значит, движение точки равнопеременное (a = a_t = —10 м/c 2 = const) с начальной скоростью v₀ = 20 м/с.

2. Составим зависимость числовых значений s и v для первых 4 с движения

3. По приведенным числовым значениям построим графики расстояний (рис. а), скорости (рис. б) и ускорения (рис. в), выбрав масштабы для изображения по осям ординат расстояний s, скорости v и ускорения а, а также одинаковый для всех графиков масштаб времени по оси абсцисс. Например, если расстояние s = 5 м изображать на графике длиной отрезка l_s = 10 мм, то 5м = μ_s*10мм, где коэффициент пропорциональности μ_s и есть масштаб по оси Os : μ_s = 5/10 = 0,5 м/мм (0,5 м в 1 мм); если модуль скорости v = 10 м/с изображать на графике длиной l_v =10 мм, то 10 м/c = μ_v * 10 мм и масштаб по оси Ov μ_v = 1 м/(с-мм) (1 м/с в 1 мм); если модуль ускорения а = 10 м/с 2 изображать отрезком l_a = 10 мм, то, аналогично предыдущему, масштаб по оси Оа μ_a = 1 м/(с 2 -мм) (1 м/с 2 в 1 мм); и наконец, изображая промежуток времени Δt = 1 с отрезком μ_t = 10 мм, получим на всех графиках масштаб по осям Ot μ_t = 0,1 с/мм (0,1 с в 1 мм).

4. Из рассмотрения графиков следует, что в течение времени от 0 до 2 с точка движется равнозамедленно (скорость v и ускорение в течение этого промежутка времени имеют разные знаки, значит, их векторы направлены в противоположные стороны); в период времени от 2 до 4 с точка движется равноускоренно (скорость v и ускорение имеют одинаковые знаки, т. е. их векторы направлены в одну сторону).

За 4 с точка прошла путь s_o_₄ = 40 м. Начав движение со скоростью v₀ = 20 м/с, точка по прямой прошла 20 м, а затем вернулась в исходное положение, имея ту же скорость, но направленную в противоположную сторону.

Если условно принять ускорение свободного падения g = 10 мс 2 и пренебречь сопротивлением воздуха, то можно сказать, что графики описывают движение точки, брошенной вертикально вверх со скоростью а₀ = 20 м/с.

Пример 6. Точка движется по траектории, изображенной на рис. 1.44, а, согласно уравнению s = 0,2t 4 (s — в метрах, t — в секундах). Определить скорость и ускорение точки в положениях 1 и 2.

Решение

Время, необходимое для перемещения точки из положения 0 (начала отсчета) в положение 1, определим из уравнения движения, подставив частные значения расстояния и времени:

Уравнение изменения скорости

Скорость точки в положении 1

Уравнение изменения касательного ускорения

Касательное ускорение точки в положении 1

Нормальное ускорение точки на прямолинейном участке траектории равно нулю. Скорость и ускорение точки в конце этого участка траектории показаны на рис.1.44, б.

Определим скорость и ускорение точки в начале криволинейного участка траектории. Очевидно, что v₁ = 11,5 м/с, а_t1 = 14,2 м/с 2 .

Нормальное ускорение точки в начале криволинейного участка

Скорость и ускорение в начале криволинейного участка показаны на рис. 1.44, в (векторы a_t₁ и a_a₁ изображены без соблюдения масштаба).

Положение 2 движущейся точки определяется пройденным путем, состоящим из прямолинейного участка 0 — 1 и дуги окружности 1 — 2, соответствующей центральному углу 90°:

Время, необходимое для перемещения точки из положения 0 в положение2,

Скорость точки в положении 2

Касательное ускорение точки в положении 2

Нормальное ускорение точки в положении 2

Ускорение точки в положении 2

Скорость и ускорения точки в положении 2 показаны на рис. 1.44, в (векторы at„ и а_Пг изображены без соблюдения масштаба).

Пример 7. Точка движется по заданной траектории (рис. 1.45, а) согласно уравнению s = 5t 3 (s — в метрах, t — в секундах). Определить ускорение точки и угол α между ускорением и скоростью в момент t₁, когда скорость точки v₁ = 135 м/с.

Решение

Уравнение изменения скорости

Время t₁ определим из уравнения изменения скорости, подставив частные значения скорости и времени:

Определим положение точки на траектории в момент 3 с:

Дуга окружности длиной 135 м соответствует центральному углу

Уравнение изменения касательного ускорения

Касательное ускорение точки в момент t_t

Нормальное ускорение точки в момент t_t

Ускорение точки в момент t_x

Скорость и ускорение точки в момент времени t₁ показаны на рис. 1.45, б.

Как видно из рис. 1.45, б

Пример 8. В шахту глубиной H = 3000 м с поверхности земли без начальной скорости брошен предмет. Определить, через сколько секунд звук, возникающий в момент удара предмета о дно шахты, достигнет поверхности земли. Скорость звука 333 м/с.

Решение

Уравнение движения свободно падающего тела

Время, необходимое для перемещения предмета от поверхности земли до дна шахты, определим из уравнения движения:

Звук распространялся с постоянной скоростью 333 м/с. Уравнение распространения звука

Время достижения звуком поверхности земли

Тогда время с момента начала движения предмета до момента достижения звуком поверхности земли

Пример 9. По заданным уравнениям движения точки x = 2t 2 , y = 2t (x и у — в метрах, t — в секундах) найти уравнение траектории, а также скорость и ускорение точки в момент времени t = 2 с.

Решение

Для определения траектории точки нужно из уравнений движения исключить параметр t — время.

Выразим t через х из первого уравнения:

и подставим это значение во второе уравнение:

Траекторией точки является парабола, симметричная относительно оси х.

Чтобы найти скорость точки, нужно определить ее составляющие по координатным осям

Находим скорость точки

При t = 2 с получаем

Находим составляющие ускорения точки

Контрольные вопросы и задания

1. Запишите формулу ускорения при прямолинейном движении.

2. Запишите формулу ускорения (полного) при криволинейном движении.

3. Тело скатывается по желобу (рис. 10.7). Какие параметры движения меняются при переходе через точку В и почему?

4. Параметры движения не меняются.

4. По заданному уравнению движения точки S = 25 + 1,5t + 6t 2 определите вид движения и без расчетов, используя законы движения точки, ответьте, чему равны начальная скорость и ускорение.

5. По заданному уравнению движения точки S = 22t — 4t 2 постройте графики скорости и касательного ускорения.

6. По графику скоростей точки определите путь, пройденный за время движения (рис. 10.8).

7. Точка движется по дуге. Охарактеризуй движение точки (рис. 10.9).

Точка движется по заданной траектории согласно уравнению s kt 3

8. Ответьте на вопросы тестового задания.

Темы 1.7, 1.8. Кинематика. Кинематика точки

ЛЕКЦИЯ 11

Дата добавления: 2017-09-01 ; просмотров: 10621 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:ФИЗИКА 10 класс : Механическое движение | Материальная точка, траектория, перемещение.Скачать

Точка движется по окружности радиусом R = 2 см согласно уравнению S = Ct3, где C = 0,1 см/с3.

Готовое решение: Заказ №8346

Тип работы: Задача

Статус: Выполнен (Зачтена преподавателем ВУЗа)

Предмет: Физика

Дата выполнения: 18.08.2020

Цена: 227 руб.

Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.

Кстати, если эта работа не по вашей теме или не по вашим данным , не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу , я смогу выполнить её в срок 1-3 дня!

Описание и исходные данные задания, 50% решения + фотография:

Точка движется по окружности радиусом R = 2 см согласно уравнению S = Ct3, где C = 0,1 см/с3. Найти тангенциальное, нормальное и полное ускорение точки в момент времени, когда линейная скорость точки V = 0,3 м/с.

Найдём нормальное ускорение точки: , где – скорость точки; – радиус кривизны траектории (радиус окружности); м/с . Найдём закон изменения мгновенной скорости точки:

Если вам нужно решить физику, тогда нажмите ➔ заказать физику.

Похожие готовые решения:

Поезд массой 500 т, двигавшийся по горизонтальному участку пути со скоростью 13 м/с
Тело массой 0,5 кг брошено вертикально вверх со скоростью 10 м/с.
На концах невесомой и нерастяжимой нити, перекинутой через неподвижный блок
Точка движется по окружности радиусом R = 2 см. Зависимость пути от времени даётся уравнением

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Урок 7. Механическое движение. Основные определения кинематики.Скачать

Точка движется по заданной траектории согласно уравнению s kt 3

Глава 7. Кинематика точки.

7.5. Уравнение движения и скорость точки при естественном способе задания движения.

7.5.1. Точка движется по траектории согласно уравнению s = 15 + 4sin πt. Указать ближайший после начала движения момент времени t₁ при котором s₁ = 17 м. (Ответ 0,167)

7.5.2. Дан график перемещения точки s = s(t). Определить скорость точки. (Ответ 0,75)

7.5.3. Точка движется по траектории согласно уравнению s = 0,5 t 2 + 4t. Определить, в какой момент времени скорость точки достигнет 10 м/с. (Ответ 6)

7.5.4. Точка движется по заданной траектории со скоростью v = 5 м/с. Определить криволинейную координату s точки в момент времени t = 18 с, если при t₀ = 0 координата s₀ = 26 м. (Ответ 116)

7.5.5. Точка движется по кривой со скоростью s = 0,5 t. Определить ее координату в момент времени t = 10 с, если при t₀ = 0 координата точки s_о = 0. (Ответ 25)

7.5.6. Скорость точки задана уравнением v = 0,2t. Определить криволинейную координату s точки в момент времени t = 10 с, если при t_o = 0 координата s₀ =0. (Ответ 10)

7.5.7. Задан закон движения точки в прямоугольной системе координат: х = 3t 2 , у = 4t 2 . Определить момент времени t, когда криволинейная координата точки s = 110 м, если при t₀ = 0 s_o= 0 и точка движется в положительном направлении координаты s. (Ответ 4,69)

7.5.8. Задан закон движения точки в прямоугольной системе координат: х = 3cos t, у = 3sin t. Определить момент времени, когда криволинейная координата точки s = 7 м, если при t₀ = 0, s₀ = 0. Точка движется в положительном направлении координаты s. (Ответ 2,33)

7.5.9. Задан закон движения точки в прямоугольной системе координат: х = 2 t, у = 3 t, z = 5 t. Определить криволинейную координату s точки в момент времени t = 10с, если при t₀ = 0, s₀ = 14 м и точка движется в положительном направлении координаты s. (Ответ 75.6)

7.5.10. Задан закон движения точки в прямоугольной системе координат: x = 2sin t, y = 2cos t. Определить криволинейную координату s в момент времени t = 5с, если при t₀=0, s₀=0 и точка движется в положительном направлении координаты s. (10)

Сборник коротких задач по теоретической механике.
Кепе О.Э.

Книга состоит из 1757 заданий которые предназначены для бысторого
контроля знаний на занятиях и зачетах а также для допуска к экзамену.
Задачи имеют ответы.

Издательство «Высшая школа» 1989 Москва

Также решение задач Кепе можно скачать здесь:
Мобильное приложение для Андроид: