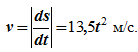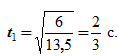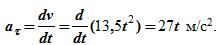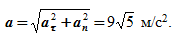Точка движется по окружности радиусом 10 см согласно уравнению s 3t2

точка движется окружности радиусом

Точка движется по окружности радиусом R=30 см с постоянным угловым ускорением ε. Определить тангенциальное ускорение а_τ точки, если известно, что за время t=4 с она совершила три оборота и в конце третьего оборота ее нормальное ускорение a_n=2,7 м/с 2 .

Материальная точка движется по окружности радиуса R = 2 м согласно уравнению S = At+Bt 3 , где А = 8 м/с; В = –0,2 м/с 3 . Найти скорость v, тангенциальное a_t, нормальное a_n и полное а ускорения в момент времени t = 3 с.

Точка движется по окружности радиусом R = 15 см с постоянным тангенциальным ускорением а_τ. К концу четвертого оборота после начала движения линейная скорость точки v₁ = 15 см/с Определите нормальное ускорение а_n2 точки через t₂ = 16 с после начала движения.

Нормальное ускорение точки, движущейся по окружности радиусом r = 4 м, задается уравнением а_n = А + Bt + Ct 2 (А = 1 м/с 2 , В = 6 м/с 3 , С = 9 м/с 4 ). Определите: 1) тангенциальное ускорение точки; 2) путь, пройденный точкой за время t₁ = 5 с после начала движения; 3) полное ускорение для момента времени t₂ = 1 с.

Точка движется по окружности радиусом 4 м. Закон ее движения выражается уравнением s = 8 – 2t 2 , м. Определить: а) в какой момент времени нормальное ускорение точки будет равно 9 м/с 2 ; б) чему равны скорость, тангенциальное и полное ускорения точки в этот момент времени?

Точка движется по окружности радиусом R = 4 м так, что в каждый момент времени ее нормальное и тангенциальное ускорения равны по модулю. В начальный момент времени t = 0 скорость точки V₀ = 0,2 м/с. Найти скорость точки в момент времени t₁ = 10 c.

Точка движется по окружности радиусом R = 8 м. В некоторый момент времени нормальное ускорение точки равно 4 м/с 2 , вектор полного ускорения образует в этот момент с вектором нормального ускорения угол 60°. Найти линейную скорость и тангенциальное ускорение точки.

Точка движется по окружности радиусом 0,4 м согласно уравнению S = 2-cos2t. Определить нормальное ускорение точки в момент времени t = π/4 с?

Точка движется по окружности радиусом R = 10 см с постоянным тангенциальным ускорением а_τ. Найти тангенциальное ускорение а_τ точки, если известно, что к концу пятого оборота после начала движения линейная скорость точки v = 79,2 см/с.

Точка движется по окружности радиусом R = 10 см с постоянным тангенциальным ускорением а_τ. Найти нормальное ускорение а_n точки через время t = 20 с после начала движения, если известно, что к концу пятого оборота после начала движения линейная скорость точки v = 10 см/с.

Точка движется по окружности радиусом R = 2 см. Зависимость пути от времени дается уравнением s = Ct 3 , где С = 0,1 см/с 3 . Найти нормальное a_n и тангенциальное a_τ ускорения точки в момент, когда линейная скорость точки v = 0,3 м/с.

Точка движется по окружности радиусом R = 4 м. Начальная скорость v₀ точки равна 3 м/с, тангенциальное ускорение а_τ = 1 м/с 2 . Для момента времени t = 2 с определить: 1) длину пути s, пройденного точкой; 2) модуль перемещения |Δr|; 3) среднюю путевую скорость ; 4) модуль вектора средней скорости | |.

Точка движется по окружности радиусом R = 2 м согласно уравнению ξ = At 3 , где A = 2 м/с 3 . В какой момент времени t нормальное ускорение а_n точки будет равно тангенциальному а_τ. Определить полное ускорение а в этот момент.

Материальная точка двигалась по окружности радиусом 2 м. Найдите путь и перемещение через 1/6 часть оборота, 1/4, 1/2 и полный оборот.

Точка движется по окружности радиусом 60 см с постоянным тангенциальным ускорением. Найти нормальное ускорение точки через 3 с после начала движения, если известно, что к концу пятого оборота после начала движения линейная скорость точки равна 5 м/с.

Нормальное ускорение точки, движущейся по окружности радиусом 4 м, задаётся уравнением a_n = At 3 (A = 0,5 м/с 5 ). Определить: 1) тангенциальное ускорение точки в момент времени 5 c; 2) путь, пройденный точкой за время 5 с после начала движения; 3) полное ускорение для момента времени 1 с.

Точка движется по окружности радиусом R = 1,20 м. Уравнение движения точки имеет вид: φ = At + Bt 3 , где А = 0,500 рад/с, В = 2,50 рад/с 3 . Определить тангенциальное а_τ, нормальное а_п и полное а ускорение точки в момент времени t = 0,954 с.

Точка движется по окружности радиуса R = 0,5 м с постоянным касательным ускорением 2 м/с 2 из состояния покоя. Определить нормальное и полное ускорения точки в момент времени t = 1 с.

Материальная точка движется по окружности радиусом R = 4 м. Закон ее движения описывается уравнением ξ = A+Bt 2 , где A = 8 м, B = –2 м/с 2 , а ξ отсчитывается вдоль окружности. Найти момент времени, когда нормальное ускорение точки равно 9 м/с 2 , а также скорость, тангенциальное и полное ускорения точки в этот момент времени.

Материальная точка движется по окружности радиусом R = 1 м. Зависимость угла поворота от времени имеет вид φ = At 4 , где A = 1 рад/с 4 . Определить линейное ускорение материальной точки через секунду после начала движения, а также угол между линейным ускорением и радиусом окружности в этот момент времени.

Материальная точка движется по окружности радиуса R = 2 м. Закон ее движения описывается уравнением ξ(t) = At 2 + Bt 3 , где А = 3 м/с 2 , В = 1 м/с 3 , а координата ξ(t) отсчитывается вдоль окружности. Найти момент времени, когда тангенциальное ускорение точки равно 18 м/с 2 , а также нормальное и полное линейное ускорение точки в этот момент времени.

Материальная точка движется по окружности радиуса R, причем φ = ωt (φ – угол между радиус-вектором точки, проведенным из некоторой точки А окружности, и прямой, соединяющей точку А и центр окружности; ω — константа). Найти тангенциальную и нормальную составляющие скорости и ускорения точки.

Точка движется по окружности радиусом 79 см с постоянным тангенциальным ускорением. Найти нормальное ускорение точки через 3 с после начала движения, если известно, что к концу пятого оборота после начала движения линейная скорость точки равна 3 м/с.

Точка движется по окружности радиусом R = 0,1 м с постоянным тангенциальным ускорением. Найти ускорение точки через 10 с после начала движения, если известно, что к концу пятого оборота после начала движения линейная скорость точки v = 0,8 м/с.

Видео:Физика - движение по окружностиСкачать

iSopromat.ru

Пример решения задачи по определению нормального, касательного и модуля полного ускорения точки, а также, угла с вектором скорости, точки, движущейся по окружности заданного радиуса и известному закону заданному уравнением.

Видео:Точка движется по окружности радиусом R=2см. Волькенштейн 1.47Скачать

Задача

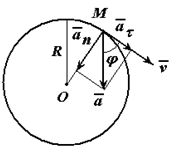
Точка движется по окружности радиуса R=4 м, закон ее движения определяется уравнением s=4,5t 3 ( s в метрах, t в секундах).

Определить модуль полного ускорения и угол φ его с вектором скорости в тот момент t₁, когда скорость будет равна 6 м/с (рисунок 1.6).

Видео:Центростремительное ускорение. 9 класс.Скачать

Решение

Дифференцируя s по времени, находим модуль вектора скорости точки

Подставляя в это выражение значение скорости, получим 6=13,5t₁ 2 , откуда находим

Касательное ускорение для любого момента времени равно

Так как для окружности радиус кривизны ρ=R, то нормальное ускорение для любого момента времени равно

Модуль вектора полного ускорения точки равен

Угол между вектором полного ускорения и вектором скорости определим следующим образом:

Видео:Физика 10 класс (Урок№4 - Равномерное движение точки по окружности.)Скачать

Точка движется по окружности радиусом 10 см согласно уравнению s 3t2

Глава 7. Кинематика точки.

7.7. Нормальное ускорение точки.

7.7.1. Точка движется с постоянной скоростью v = 30 см/с по дуге ок­ружности радиуса r = 2 м. Определить нормальное ускорение точки в см/с 2 . (Ответ 4,5)

7.7.2. Дан график скорости v = v(t) движения точки по окружности радиуса R. Найти время t в интервале от 0 до 4 с, при котором нор­мальное ускорение точки будет максималь­ным. (Ответ 2)

7.7.3. По окружности движется точка согласно уравнению s = 5t — 0,4t 2 . Определить время t когда нормальное ускорение а_n = 0. (Ответ 6,25)

7.7.4. Определить радиус закругления трассы бобслея, если при скорос­ти спуска 120 км/ч нормальное ускорение саней а_n = 2g. (Ответ 56,6)

7.7.5. Дан график скорости v = v(t) движения точки по окружности радиуса R. Найти время t, при котором нормальное ускорение а_n = 0. (Ответ 2,5)

7.7.6. Автомобиль движется по горизонтальной дороге с постоянной скоростью v = 90 км/ч. Определить радиус закругления дороги в момент времени, когда нормальное ускорение центра автомобиля а_n = 2,5 м/с. (Ответ 250)

7.7.7. Дан график скорости v = v(t) движения точки по окружности радиуса 5 м. Определить нормальное ускорение точки в момент време­ни 3 с. (Ответ 1,25)

7.7.8. Дано уравнение движения точки по траектории s = 5 t. Определить радиус кривизны траектории, когда нормальное ускорение точки а_n = 3 м/с 2 . (Ответ 8.33)

7.7.9. Дан график изменения криволинейной координаты s = s(t) движения точки по ок­ружности радиуса R. Найти момент времени t, когда нормальное ускорение точки а_n = 0. (Ответ 1)

7.7.10. Электровоз движется по дуге окружности радиуса R = 300 м Определить максимальную скорость электровоза в км/ч, при которой нормальное ускорение не превышало бы 1 м/с 2 .
(Ответ 62,4)

7.7.11. Центрифуга для тренировки пилотов устроена так, что центр ка­бины с человеком находится на расстоянии r = 5 м от оси вращения. Определить скорость центра кабины в случае, когда ее нормальное ускорение а_n = 5 g. (Ответ 15,7)

7.7.12. Дан график скорости v = v(t) движения точки по окружности радиуса 6 м. Определить нормальное ускорение точки в момент време­ни t = 3 с. (Ответ 2,67)

7.7.13. Дан график скорости v = v(t) движения точки по окружности радиуса 8 м. Определить момент времени t, когда нормальное ускоре­ние точки а_n = 0,5 м/с. (Ответ 3)

7.7.14. Самолет летит по круговой траектории, радиус которой r = 10 км. Определить скорость самолета в км/ч, если его нормальное ускорение а_n = 6,25 м/с 2 . (Ответ 900)

7.7.15. Дано уравнение движения точки по траектории: s = 0,1 t 2 + 0,2 t. Определить ее нормальное ускорение в момент времени t = 6 с. В положении, занимаемом точкой в этот момент, радиус кри­визны траектории ρ = 0,6 м. (Ответ 3,27)

7.7.16. Точка движется по окружности, радиус которой r = 30 см, со скоростью v = In t. Определить нормальное ускорение точки в мо­мент времени t = 12 с. (Ответ 20,6)

7.7.17. Дано уравнение движения точки по траектории s = 0,6t 2 . Опре­делить нормальное ускорение точки в момент времени, когда ее коор­дината s = 30 м и радиус кривизны траектории ρ = 15 м. (Ответ 4,80)

7.7.18. По окружности, радиус которой r = 7 м, движется точка согласно уравнению s = 0,3t 2 . Определить время, когда нормальное ускорение точки а_n = 1,5 м/с 2 . (Ответ 5,40)

7.7.19. Точка движется по окружности, радиус которой r = 20 м, со скоростью v = е t . Определить момент времени, когда нормальное ускорение точки а_n = 3 м/с 2 . (Ответ 2,05)

7.7.20. Точка движется по окружности радиуса R = 7 м согласно уравнению s = 0,7t 2 . Определить координату s точки в момент времени когда ее нормальное ускорение а_n = 3 м/с 2 . (Ответ 7,50)

🎦 Видео

Равномерное движение точки по окружности | Физика 10 класс #7 | ИнфоурокСкачать

Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Вращательное движение. 10 класс.Скачать

Урок 47. Неравномерное движение по окружности. Тангенциальное ускорениеСкачать

Ускорение при равномерном движении по окружностиСкачать

Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

ЦЕНТРОСТРЕМИТЕЛЬНОЕ УСКОРЕНИЕ кинематика 9 и 10 классСкачать

Движение материальной точки по окружности | Физика ЕГЭ, ЦТСкачать

Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

Криволинейное, равномерное движение материальной точки по окружности. Практическая часть. 9 класс.Скачать

Физика 10 Равномерное движение точки по окружностиСкачать

Уравнение равномерного прямолинейного движения | Физика 10 класс #3 | ИнфоурокСкачать

Движение по окружности. Нормальное и тангенциальное ускорение | 50 уроков физики (4/50)Скачать

УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

9 класс урок №10 Центростремительное ускорениеСкачать

Физика 9 класс. Движение по окружностиСкачать