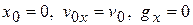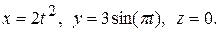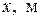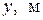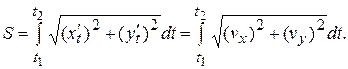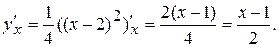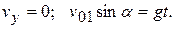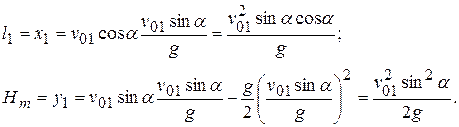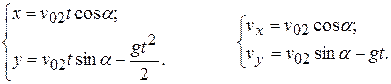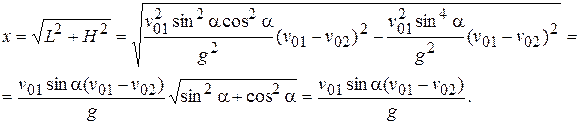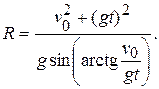- Реферат.Справочник
- Решенные задачи по физике
- Точка движется по кривой так что её координаты на плоскости описывают
- Условие
- Решение
- Кинематика поступательного движения материальной точки
- Координаты материальной точки, движущейся в плоскости XOY, описываются уравнениями : x = — 4t, y = 6 + 2t?
- Движение материальной точки задано уравнением x = — 4 + 2t + 2t2?
- Уравнение координаты материальной точки, движущейся вдоль оси Оx, имеет вид x = 10 + 4t + 2t в квадрате (величины выражены в СИ)?
- Движение материальной точки описывается уравнением x = 20t Найдите : а) начальную координату точки ; б) модуль и направление ее скорости?
- Движение материальной точки описывается уравнением х = 12t?
- По графику движения записать уравнение координаты движущегося тела?
- Движение материальной точки в данной системе отсчета описывается уравнениями у = 1 + 2t, х = 2 + t?
- Уравнения движения материальной точки в плоскости XOY имеют вид x = 25t, м, у = 0, 2 + t, м?
- Точка М совершает движение на плоскости XOY?
- Движение материальной точки описывается уравнением x = 3 + 2t?
- Уравнение координаты материальной точки, движущейся вдоль оси ОХ имеет вид : Х = 10 + 4t = 2t² (величины выражены в СИ)?
- 📸 Видео
Условие
Точка движется по кривой так, что её координаты на плоскости описывают Описание Точка Движется по кривой так, что её координаты на плоскости описываются уравнениями:X=A1+B1t+C1t^3,Y=A2+B2t+C2t^2.Найдите перемещение точки за время от 0 до t, а также скорость, полное, нормально и тангенциальное ускорение точки в момент времени t. t=5,0;A1=1,0;B1=0,2;C1=0,01;A2=2;B2=0,4;C2=0,4.
Решение
Перемещение точки по теореме Пифагора: Находим проекции по x и y: Тогда перемещение: Скорость: Найдём проекции как производные от координаты: Тогда скорость: Ускорение: Найдём проекции как производные от скорости: Тогда скорость: Нормальное ускорение: Тангенциальное ускорение:
Видео:Координаты на плоскости и в пространстве. Вебинар | МатематикаСкачать

Кинематика поступательного движения материальной точки
Кинематика – раздел механики, который изучает движение тел без рассмотрения причин, его вызывающих.
Материальная точка – тело, размерами которого в условиях данной задачи можно пренебречь.
Траектория – геометрическое место точек, последовательно занимаемых движущимся телом.
Поступательное движение – движение, при котором любая прямая, жестко связанная с движущимся телом, остается параллельной своему первоначальному положению.
Степени свободы – число независимых координат, полностью определяющих положение материальной точки в пространстве.
Скорость – первая производная перемещения по времени.
Ускорение – быстрота изменения скорости по модулю и по направлению, первая производная скорости по времени или вторая производная перемещения по времени.
Годограф скоростей – кривая, которую описывает в пространстве конец вектора скорости.
Нормальная составляющая ускорения (нормальное ускорение) – показывает быстроту изменения скорости по направлению, направлена перпендикулярно к касательной к траектории движения, т.е. вдоль главной нормали.
Тангенциальная составляющая ускорения (тангенциальное ускорение) – показывает быстроту изменения скорости по модулю, направлена по касательной к траектории движения ( 

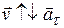

| Уравнение движения материальной точки: |  . . |
| Кинематические уравнения движения материальной точки: | 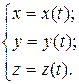 |
| Вектор перемещения материальной точки: |  . . |
| Средняя скорость: | 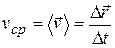 . . |
| Мгновенная скорость: |  . . |
| Среднее ускорение: | 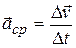 . . |
| Мгновенное ускорение: |  . . |
| Нормальное ускорение: |  . . |
| Тангенциальное ускорение: |  . . |
| Полное ускорение материальной точки: |  |
| Радиус-вектор материальной точки: |  . . |
| Уравнение мгновенной скорости: |  |
| Уравнение мгновенного ускорения: |  |
| Модули радиус-вектора, вектора мгновенной скорости и вектора ускорения: |  |
| Модуль мгновенной скорости: |  . . |
Длина пути, пройденного материальной точкой за промежуток времени 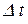 : : |  . . |
Примеры решения задач
Записать кинематические уравнения движения точек для случаев, представ ленных на рисунках.
Общий вид кинематического уравнения движения материальной точки:
Рассмотрим случай движения, представленный на рис. 1.1,а.
Материальная точка А движется вдоль оси Ох, т.е. движение одномерное, поэтому оно будет описываться одним кинематическим уравнением (проекцией уравнения на координатную ось Ох):
На рисунке точка А лежит левее точки отсчета О, следовательно, начальная координата будет отрицательной: 




Искомое уравнение имеет вид:
На рис.1.1,в материальная точка движется в плоскости Оху, т.е. имеет две степени свободы, поэтому ее движение будет описываться системой, состоящей из двух кинематических уравнений (проекций кинематического уравнения на оси Ох и Оу).
В проекции на ось Ох получаем:
(проекции векторов скорости и ускорения равны нулю, так как эти векторы перпендикулярны координатной оси); в проекции на ось Оу:

Искомая система уравнений имеет вид:
Случаи, представленные на рис. 1.1,б и 1.1,г рассмотреть самостоятельно.
Задача 1.2
Определить модуль скорости материальной точки в момент времени 2 с, если радиус-вектор точки изменяется по закону: 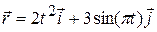
Дано: 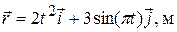 ; ;  . Найти . Найти  | Решение Общий вид уравнения радиус-вектора в декартовой системе координат:  . Сравнив данное уравнение с уравнением, представленным в условии задачи, получаем составляющие радиус-вектора . Сравнив данное уравнение с уравнением, представленным в условии задачи, получаем составляющие радиус-вектора  , , |
то есть, проекции на координатные оси x, y и z равны
Найдем составляющие вектора скорости, т.е. проекции вектора скорости на координатные оси Ох и Оу:
Вектор скорости в декартовой системе координат имеет вид:

Модуль вектора скорости определяется по формуле:

После подстановки получаем
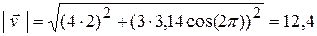
Ответ: 
Точка движется в плоскости так, что ее движение описывается уравнениями 
Дано:  Найти Найти   | Решение: Запишем уравнение траектории движения материальной точки. Заданы уравнения изменения двух координат точки от времени, следовательно, тело движется в плоскости Оху. Необходимо записать уравнение, связывающее между собой координаты, для этого выразим из уравнения  время и подставим во второе уравнение: время и подставим во второе уравнение: 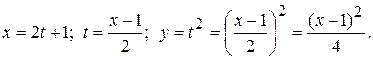 Построим график траектории движения материальной точки, для этого составим таблицу: Построим график траектории движения материальной точки, для этого составим таблицу: | ||||||
| 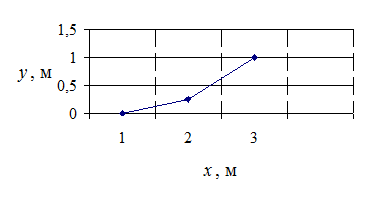 Рис. 1.2 Рис. 1.2 |
Запишем уравнение радиус-вектора:

Скорость – первая производная радиус-вектора по времени, т.е.
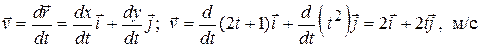
Ускорение – вторая производная радиус-вектора по времени или первая производная скорости по времени:

Найдем модуль вектора скорости:
Подставив значение времени, получаем
Найдем путь, пройденный материальной точкой за 1 секунду, т.е. длину кривой АВ:
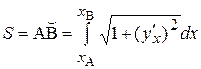
Производная уравнения траектории
Координата материальной точки за 1 с движения по оси Ох изменяется от 1 м до 3 м, что было определено в таблице и отражено на графике траектории, тогда
т.е. интеграл привели к табличному виду:

Ответ:
Из одной точки в один и тот же момент времени под углом 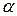

Дано: 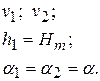 Найти Найти 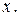 | Решение Сделаем чертеж к данной задаче. Исходя из построений (рис.1.3) расстояние между двумя камнями  , где , где  . . |
Запишем кинематические уравнения движения материальной точки в векторном виде:
 Рис.1.3 Рис.1.3 |
Рассмотрим движение первого камня, брошенного со скоростью 
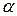
Первый камень находится в точке наивысшего подъема (по условию). Вектор скорости, направленный по касательной к траектории движения, будет параллелен оси Оx и его проекция на ось Оy будет равна нулю:
Тогда время движения камней

Координаты первого камня в данный момент времени:
Рассмотрим движение второго камня, брошенного со скоростью 
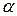
Запишем проекции кинематических уравнений на координатные оси:
Координаты второго камня в момент времени 
Найдем расстояния L и H:

Ответ: х = 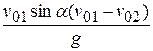
Тело брошено горизонтально со скоростью 15 м/с. Пренебрегая сопротивлением воздуха, определить радиус кривизны траектории тела через 2 с после начала движения.
Дано:  Найти Найти 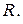 | Решение Сделаем чертеж к данной задаче (рис.1.4). |
 Рис.1.4 Рис.1.4 | Кинематические уравнения движения материальной точки:  |
Запишем проекции этих уравнений на координатные оси:
Для определения радиуса кривизны траектории воспользуемся формулой нормального ускорения:

где 

где 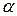
Из построений следует, что
Радиус кривизны траектории
Подставляя значения: 
Задачи для самостоятельного решения
1. Две материальные точки движутся согласно уравнениям 
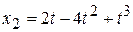
2. Материальная точка движется по закону 
3. Тело, движущееся равноускоренно, проходит участок пути 60 м за 10 с, при этом скорость на данном участке возросла в 7 раз. Определить ускорение тела 
4. При падении камня в колодец его удар о поверхность воды доносится через 5 с. Принимая скорость звука, равной 330 м/с, определить глубину колодца (107 м).
5. Точка движется в плоскости так, что ее движение описывается уравнениями 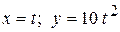
6. С башни высотой 25 м брошен камень со скоростью 15 м/с под углом 30 о к горизонту. Какое время камень будет в движении? На каком расстоянии от основания башни он упадет на землю? Какова будет скорость камня в момент удара о землю? (3,15 с; 40.94 м; 26,7 м/с).
1. Как направлен вектор мгновенной скорости относительно траектории?
2. Как направлены тангенциальное и нормальное ускорения относительно радиуса кривизны траектории?
3. Определите вид движения, при котором выполняются условия: 


4. При каком движении 
5. Начертите графики 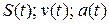
6. Сколько степеней свободы имеет материальная точка при движении в пространстве, при движении на плоскости?
7. Как направлен вектор ускорения к траектории движения, к годографу скоростей?
8. Радиус-вектор точки изменяется: а) только по модулю, б) только по направлению. Что можно сказать о траектории?
Видео:11. Прямая в пространстве и ее уравненияСкачать

Координаты материальной точки, движущейся в плоскости XOY, описываются уравнениями : x = — 4t, y = 6 + 2t?
Физика | 5 — 9 классы
Координаты материальной точки, движущейся в плоскости XOY, описываются уравнениями : x = — 4t, y = 6 + 2t.
Записать уравнение траектории y = y(x).
Найти начальные координаты движущейся точки и ее координаты через 1 с после начала движения?
y = 6 + 2t = 6 + 2 * ( — x / 4) = 6 — x / 2, y = 6 — 0, 5x — уравнение у = у(t)
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Движение материальной точки задано уравнением x = — 4 + 2t + 2t2?
Движение материальной точки задано уравнением x = — 4 + 2t + 2t2.
Определите : а) начальную координату ; б)начальную скорость ; в) ускорение ; г) координату точки через 5с ;
Видео:Определение координаты движущегося тела | Физика 9 класс #3 | ИнфоурокСкачать

Уравнение координаты материальной точки, движущейся вдоль оси Оx, имеет вид x = 10 + 4t + 2t в квадрате (величины выражены в СИ)?
Уравнение координаты материальной точки, движущейся вдоль оси Оx, имеет вид x = 10 + 4t + 2t в квадрате (величины выражены в СИ).
Определите характер движения точки.
Найдите начальную координату, начальную скорость и ускорение точки.
Видео:Урок 18 (осн). Координаты тела. График движения. График скоростиСкачать

Движение материальной точки описывается уравнением x = 20t Найдите : а) начальную координату точки ; б) модуль и направление ее скорости?
Движение материальной точки описывается уравнением x = 20t Найдите : а) начальную координату точки ; б) модуль и направление ее скорости.
Постойте : а) график зависимости x(t) ; б) график зависимости u(t) Найдите графически и аналитически : а)координату точки через 15 с.
После начала движения ; б) момент времени, когда точка будет иметь координату x = 100м.
Видео:найти уравнение кривой, по которой двигается точка МСкачать

Движение материальной точки описывается уравнением х = 12t?
Движение материальной точки описывается уравнением х = 12t.
Опишите характер движения точки, найдите начальную координату, модуль и направление вектора скорости.
Чему равно ускоиение материальной точки?
В какой момент координата точки будет равна 72 м?
Видео:Движение точки тела. Способы описания движения | Физика 10 класс #2 | ИнфоурокСкачать

По графику движения записать уравнение координаты движущегося тела?
По графику движения записать уравнение координаты движущегося тела.
Видео:ЕГЭ по математике. Профильный уровень. Задание 7. Закон движения. ПроизводнаяСкачать

Движение материальной точки в данной системе отсчета описывается уравнениями у = 1 + 2t, х = 2 + t?
Движение материальной точки в данной системе отсчета описывается уравнениями у = 1 + 2t, х = 2 + t.
Найти уравнение траектории.
Построить траекторию на плоскости XOY.
Указать положение точки t = 0, направление и скорость движения.
Если можно то с графиком и с объяснением.
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Уравнения движения материальной точки в плоскости XOY имеют вид x = 25t, м, у = 0, 2 + t, м?
Уравнения движения материальной точки в плоскости XOY имеют вид x = 25t, м, у = 0, 2 + t, м.
Определите уравнение траектории материальной точки.
Видео:Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

Точка М совершает движение на плоскости XOY?
Точка М совершает движение на плоскости XOY.
Координаты точки в зависимости от времени изменяются так :
х = — 4 м / с • t, у = 6 м + 2 м / с • t.
Запишите уравнение траектории у = у(х) точки М.
Найдите начальные координаты движущейся точки и ее координаты через 1 с после начала движения.
Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Движение материальной точки описывается уравнением x = 3 + 2t?
Движение материальной точки описывается уравнением x = 3 + 2t.
Найдите начальную координату, проекцию скорости, её модуль направление.
Определите координату точки через 5 с после начала движения.
Через сколько секунд координата точки будет равна 9м?
Постройте график скорости v(t).
Видео:УРАВНЕНИЕ ПРЯМОЙ на плоскости 8 и 9 классСкачать

Уравнение координаты материальной точки, движущейся вдоль оси ОХ имеет вид : Х = 10 + 4t = 2t² (величины выражены в СИ)?
Уравнение координаты материальной точки, движущейся вдоль оси ОХ имеет вид : Х = 10 + 4t = 2t² (величины выражены в СИ).
Опредилите характер движения точки.
Найдитеначальную координату, начальную скорость и ускорение точки.
Вы зашли на страницу вопроса Координаты материальной точки, движущейся в плоскости XOY, описываются уравнениями : x = — 4t, y = 6 + 2t?, который относится к категории Физика. По уровню сложности вопрос соответствует учебной программе для учащихся 5 — 9 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.
📸 Видео
кинематика точкиСкачать

Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Урок 87. Движение по наклонной плоскости (ч.1)Скачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Движение материальной точки по окружности | Физика ЕГЭ, ЦТСкачать

Материальная точка движется прямолинейно по закону x(t) В какой момент времени ее скорость = 2 м/с?Скачать

Урок 7. Механическое движение. Основные определения кинематики.Скачать