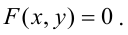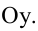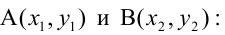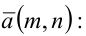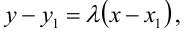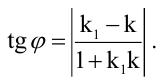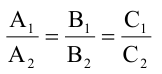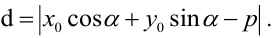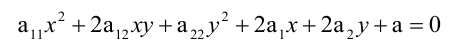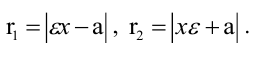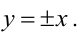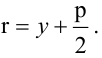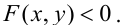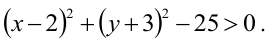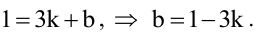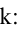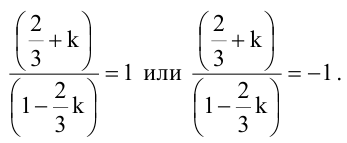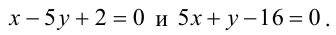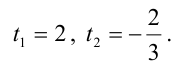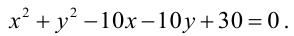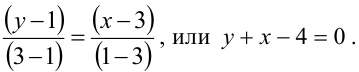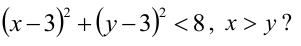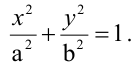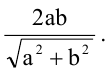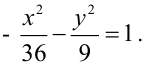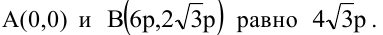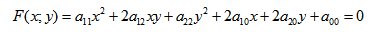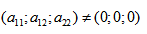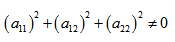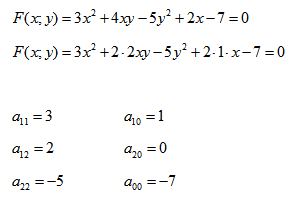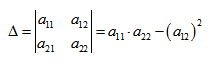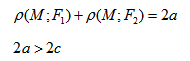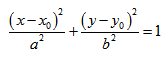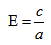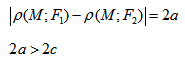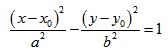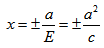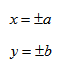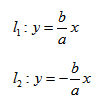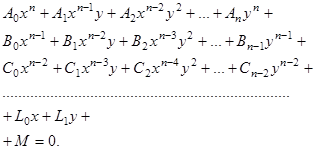Содержание:
- Уравнения прямых и кривых на плоскости
- Кривые второго порядка
- Кривая второго порядка — это некоторая линия на плоскости, которая в декартовой системе координат задается общим уравнением:
- Имеем дело с уравнением второй степени, в котором коэффициенты при старших членах — при вторых степенях одновременно не нули.
- Гипербола — множество точек на плоскости для каждой из которых абсолютная величина разности расстояний до двух данных точек F1 и F2 есть величина постоянная, меньшая расстояния между этими точками.
- Парабола — множество точек на плоскости для каждой из которых расстояние до данной точки F равно расстоянию до данной прямой f.
- Классификация плоских кривых
- 📹 Видео
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Уравнения прямых и кривых на плоскости
Уравнения кривых в большом количестве встречаются при чтении экономической литературы. Укажем некоторые из этих кривых.
Кривая безразличия — кривая, показывающая различные комбинации двух продуктов, имеющих одинаковое потребительское значение, или полезность, для потребителя.
Кривая потребительского бюджета — кривая, показывающая различные комбинации количеств двух товаров, которые потребитель может купить при данном уровне его денежного дохода.
Кривая производственных возможностей — кривая, показывающая различные комбинации двух товаров или услуг, которые могут быть произведены в условиях полной занятости и полного объема производства в экономике с постоянными запасами ресурсов и неизменной технологией.
Кривая инвестиционного спроса — кривая, показывающая динамику процентной ставки и объем инвестиций при разных процентных ставках.
Кривая Филлипса — кривая, показывающая существование устойчивой связи между уровнем безработицы и уровнем инфляции.
Кривая Лаффера — кривая, показывающая связь между ставками налогов и налоговыми поступлениями, выявляющая такую налоговую ставку, при которой налоговые поступления достигают максимума.
Уже простое перечисление терминов показывает, как важно для экономистов умение строить графики и анализировать уравнения кривых, каковыми являются прямые линии и кривые второго порядка — окружность, эллипс, гипербола, парабола. Кроме того, при решении большого класса задач требуется выделить на плоскости область, ограниченную какими-либо кривыми, уравнения которых заданы. Чаще всего эти задачи формулируются так: найти наилучший план производства при заданных ресурсах. Задание ресурсов имеет обычно вид неравенств, уравнения которых даны. Поэтому приходится искать наибольшее или наименьшее значения, принимаемые некоторой функцией в области, заданной уравнениями системы неравенств.
В аналитической геометрии линия на плоскости определяется как множество точек, координаты которых удовлетворяют уравнению
Пусть на плоскости задана прямоугольная декартова система координат. Прямая на плоскости может быть задана одним из уравнений:
1. Общее уравнение прямой:
Вектор 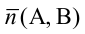
2. Уравнение прямой с угловым коэффициентом:
где 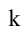
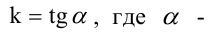
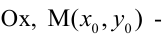
Уравнение (2.2) принимает вид 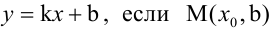
3. Уравнение прямой в отрезках:
где а и b — величины отрезков, отсекаемых прямой на осях координат.
4. Уравнение прямой, проходящей через две данные точки —
5. Уравнение прямой, проходящей через данную точку 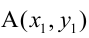
6. Нормальное уравнение прямой:
где 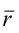
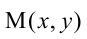
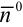
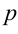
Нормальное уравнение прямой в координатной форме имеет вид:
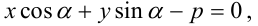
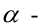
Уравнение пучка прямых с центром в точке 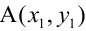
где 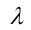
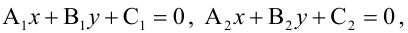
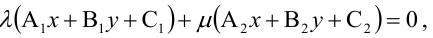
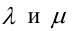
Величина угла между прямыми 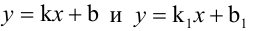
Равенство 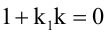
Для того, чтобы два уравнения

Уравнения (2.7), (2.8) задают две различные параллельные прямые, если 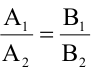
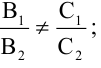
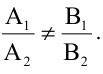
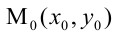
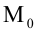
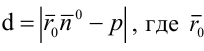
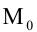
Общее уравнение кривой второго порядка имеет вид:
Предполагается, что среди коэффициентов уравнения 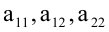
Уравнение окружности с центром в точке 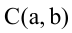

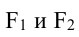
Эллипс, заданный уравнением (2.10), симметричен относительно осей координат.
Параметры а и b называются полуосями эллипса.
Пусть 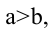
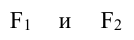
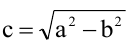
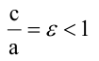
Расстояния от точки 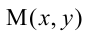
Если же 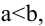
Если а=b, то эллипс является окружностью с центром в начале координат радиуса а.
Гиперболой называется геометрическое место точек, разность расстояний которых от двух данных точек 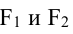
Каноническое уравнение гиперболы:
Гипербола, заданная уравнением (2.11), симметрична относительно осей координат. Она пересекает ось 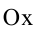
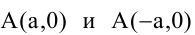
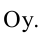
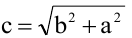
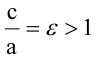
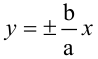
Расстояния от точки 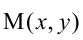
Гипербола, у которой а=b, называется равносторонней, ее уравнение 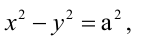
Гиперболы 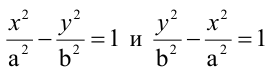
Каноническое уравнение параболы имеет два вида:
1. 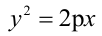
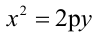
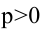
Парабола, уравнение которой 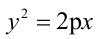
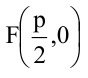
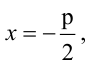
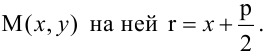
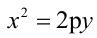
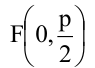
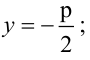
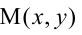
Уравнение 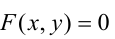
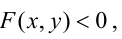
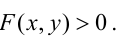
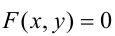
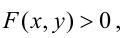
Прямая, уравнение которой 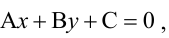
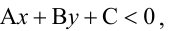
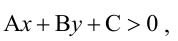
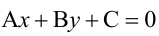
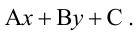
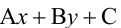
Точно так же решаются и нелинейные неравенства с двумя неизвестными.
Например, решим неравенство 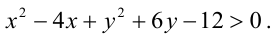
Уравнение 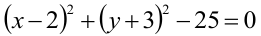
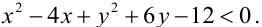
Пример:
Составьте уравнения прямых, проходящих через точку А(3,1) и наклоненных к прямой 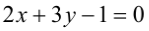
Решение:
Будем искать уравнение прямой в виде 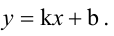
Величина угла между прямыми 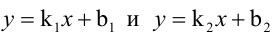
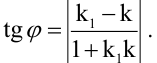
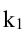
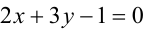
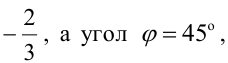
Имеем два значения 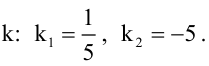
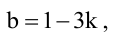
Пример:
При каком значении параметра t прямые, уравнения которых 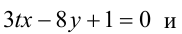
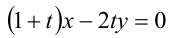
Решение:
Прямые, заданные общими уравнениями, параллельны, если коэффициенты при x и y пропорциональны, т.е. 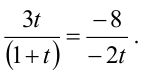
Пример:
Найти уравнение общей хорды двух окружностей: 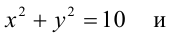
Решение:
Найдем точки пересечения окружностей, для этого решим систему уравнений: 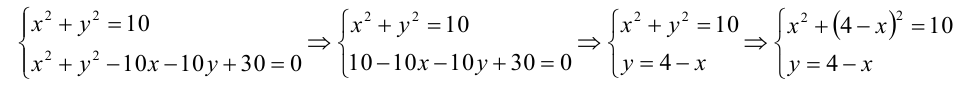
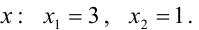
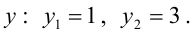
Пример:
Как расположены на плоскости точки, координаты которых удовлетворяют условиям
Решение:
Первое неравенство системы определяет внутренность круга, не включая границу, т.е. окружность с центром в точке (3,3) и радиуса 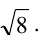
Пример:
Вычислить длину стороны квадрата, вписанного в эллипс, уравнение которого
Решение:
Пусть 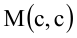
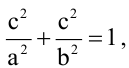
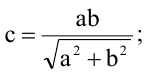
Пример:
Зная уравнение асимптот гиперболы 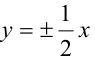
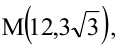
Решение:
Запишем каноническое уравнение гиперболы: 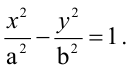
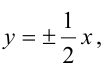
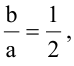
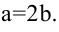
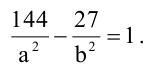
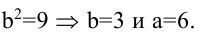
Пример:
Вычислить длину стороны правильного треугольника АВС, вписанного в параболу с параметром р, предполагая, что точка А совпадает с вершиной параболы.
Решение:
Каноническое уравнение параболы с параметром р имеет вид 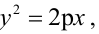
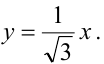
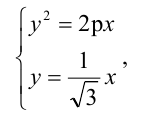
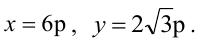
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Плоскость и прямая в пространстве
- Определитель матрицы
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Производные тригонометрических функции
- Производная сложной функции
- Пределы в математике
- Функции многих переменных
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:§31.1 Приведение уравнения кривой к каноническому видуСкачать

Кривые второго порядка
Видео:Тип кривой второго порядкаСкачать

Видео:Кривые второго порядкаСкачать

Кривая второго порядка — это некоторая линия на плоскости, которая в декартовой системе координат задается общим уравнением:
Видео:Определить тип кривой (эллипс)Скачать

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Имеем дело с уравнением второй степени, в котором коэффициенты при старших членах — при вторых степенях одновременно не нули.
Видео:Приведение кривой второго порядка к каноническому виду. ПримерСкачать

или можно встретить следующую форму записи:
Видео:Кривые второго порядка. Парабола. Приведение к каноническому виду и чертежСкачать

К кривым второго порядка относятся окружность, эллипс, гипербола и парабола.
Покажем на примере определение значений коэффициентов.
Рассмотрим кривую второго порядка:
Видео:Лекция 31.1. Кривые второго порядка. ЭллипсСкачать

Вычислим определитель из коэффициентов:
Если Δ = 0, кривая второго порядка параболического типа,
если Δ > 0, кривая второго порядка эллиптического типа,
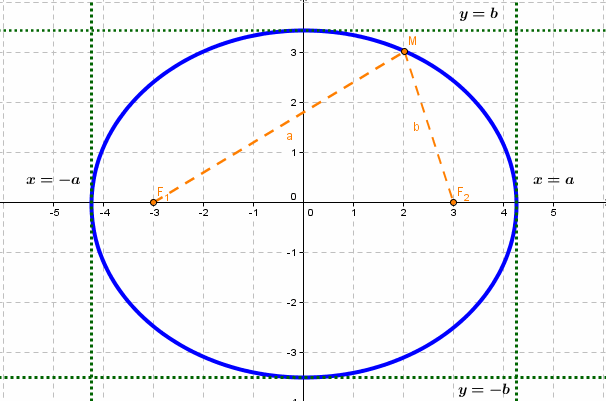
если Δ F1 и F2 — фокусы.
 |
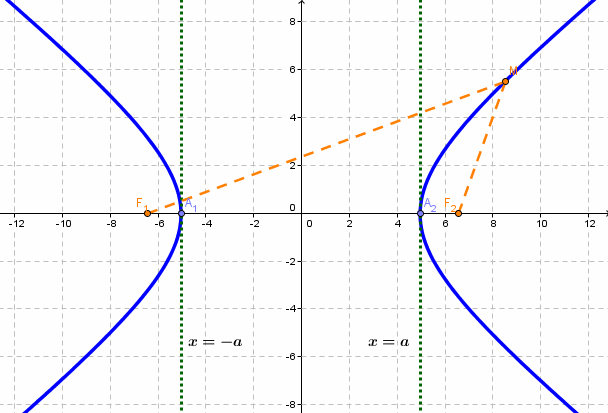 |
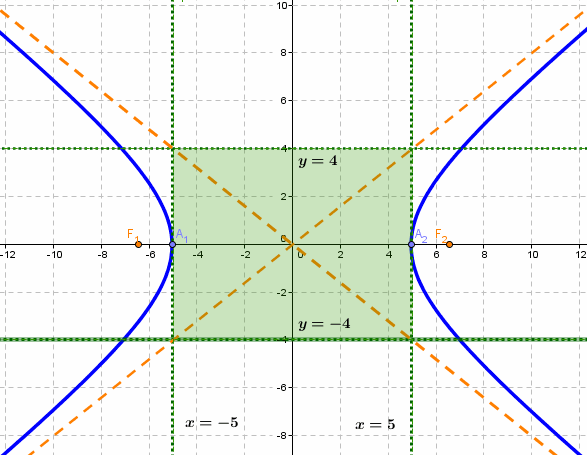 | 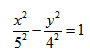 |
Парабола — множество точек на плоскости для каждой из которых расстояние до данной точки F равно расстоянию до данной прямой f.
F — фокус параболы, f — директриса параболы.
Видео:Определить тип кривой (гипербола)Скачать
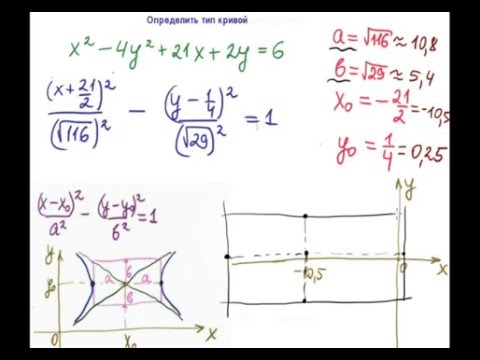
Классификация плоских кривых
В этом параграфе рассмотрим классификацию плоских кривых.
Так как характерные особенности формы кривой и её свойства определяются особенностями и свойствами соответствующего ей уравнения, то естественно положить в основу классификации кривых природу их уравнений – подразделение уравнений на алгебраические и трансцндентные. Здесь, однако, возникает затруднение, заключающееся в том, что природа уравнения кривой зависит не только от природы самой кривой, но и от той системы координат, к которой отнесена кривая. Одна и та же кривая в одной системе координат может выражаться алгебраическим уравнением, а в другой – трансцендентным. Более того иногда достаточно изменить положение системы и уравнение кривой, которое было алгебраическим, становится трансцендентным. Так, например, в полярной системе координат уравнение окружности с центром в полюсе имеет вид 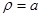
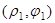
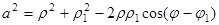
Указанный недостаток отсутствует, однако, у прямоугольной декартовой системы координат. Параллельное смещение и поворот этой системы не меняют не только природу уравнения этой кривой, но и степень этого уравнения, если оно было алгебраическим. Естественно поэтому подразделить все кривые на алгебраические и трансцендентные соответственно тому, будут ли их уравнения алгебраическими или трансцендентными в прямоугольной системе координат.
а) Алгебраические кривые
Внутри обширного семейства алгебраических линий в свою очередь производят подразделение кривых, в основу которого полагается понятие порядка кривой, определяемого степенью её уравнения.
Соответственно этому алгебраической кривой n-го порядка называется кривая, уравнение которой, после освобождения его от дробей и радикалов, записывается в декартовой системе координатв виде
Очевидно, число членов уравнения равно 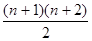
Если левая часть уравнения кривой разлагается на множители 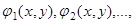
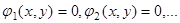
В частности, когда левая часть уравнения кривой, которую мы обозначим через f (x, y), является однородной функцией n-го измерения, кривая вырождается в систему прямых линий. Действительно, по известному свойству однородных функций, мы, полагая 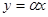
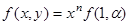
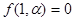
Приравнивая к нулю каждый множитель, получим систему n прямых (среди которых могут быть и мнимые).
Рассмотрим разновидности алгебраических кривых.
Класс алгебраической кривой. Формулы Плюккера.
Алгебраические кривые классифицируются не только по их порядку, но и по их классу и роду (жанру).
Класс алгебраической кривой определяется степенью её уравнения в тангенциальных координатах – так называются коэффициенты u и v в уравнениях прямых 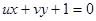
класс кривой может быть также определён числом касательных, действительных и мнимых, которые можно провести к этой кривой из произвольной точки, не лежащей на ней.
Для получения тангенциального уравнения кривой и, следовательно, для определения её класса, представим себе, что данная кривая 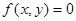
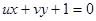
Так, например, желая найти тангенциальное уравнение окружности x 2 +y 2 =1, пересечём её прямой 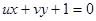
Если, наоборот, необходимо перейти от тангенциального уравнения f (u, v)=0 кривой к её обычному уравнению, то следует присоединить к этому уравнению уравнение 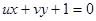
Так, например, если дана в тангенциальных координатах кривая u+v+uv=0, то, желая иметь её обычное уравнение, рассмотрим пучок прямых 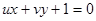
Порядок и класс линии, вообще говоря не совпадают, за исключением кривых второго порядка, которые одновременно являются кривыми второго класса. В общем случае при определении класса кривой приходится принимать во внимание не только её порядок, но и ряд её характерных особенностей – наличие у неё двойных точек, точек перегиба, двойных касательных и т.д. Именно, если n – порядок кривой, k – класс кривой, d – число двойных точек (узловых и изолированных), r – число точек возврата, t – число двойных касательных (т.е. прямых, касающихся кривой в двух точках), w – число точек перегиба кривой, то между всеми этими величинами существуют следующие соотношения:
k=n (n – 1) – 2d – 3r, n=k (k – 1) – 2t – 3w,
w=3n (n – 2) – 6d – 8r, r=3k (k – 2) – 6t – 8w.
Эти равенства называются формулами Плюккера и были приведены им впервые в его «Системе аналитической геометрии на плоскости» в 1834 году.
📹 Видео
Семинар №9 "Приведение уравнения второго порядка к каноническому виду"Скачать

Кривые второго порядка. Эллипс. Приведение к каноническому виду и чертежСкачать

Пример определения кривой второго порядкаСкачать

Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Приводим уравнение кривой 2 порядка к каноническому видуСкачать

Лекция 31.3. Кривые второго порядка. Парабола.Скачать

Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

Видеоурок "Гипербола"Скачать