Когда научный руководитель сказал мне о необходимости указать на графике R² (р квадрат), я растерялся. В тот момент я не знал о трендах в диаграммах и графиках Excel. Этот материал поможет сориентироваться начинающим.
- Что такое R² в Экселе
- Стоит ли добиваться максимального значения R²
- Как использовать тренд для прогноза
- Excel расчет линии тренда
- Добавление линии тренда на график
- Уравнение линии тренда в Excel
- Линейная аппроксимация
- Экспоненциальная линия тренда
- Логарифмическая линия тренда в Excel
- Полиномиальная линия тренда в Excel
- Процедура прогнозирования
- Способ 1: линия тренда
- Способ 2: оператор ПРЕДСКАЗ
- Способ 3: оператор ТЕНДЕНЦИЯ
- Способ 4: оператор РОСТ
- Способ 5: оператор ЛИНЕЙН
- Способ 6: оператор ЛГРФПРИБЛ
- 1-й способ расчета значений линейного тренда в Excel с помощью графика
- 2-й способ расчета значений линейного тренда в Excel — функция ЛИНЕЙН
- 3-й способ расчета значений линейного тренда в Excel — функция ТЕНДЕНЦИЯ
- 4-й способ расчета значений линейного тренда в Excel — функция ПРЕДСКАЗ
- 5-й способ расчета значений линейного тренда в Excel — Forecast4AC PRO
- Присоединяйтесь к нам!
- Периодические линии тренда в прогнозировании объемов продаж
- 💥 Видео
Видео:Как в Excel добавить линию на график быстроСкачать

Что такое R² в Экселе
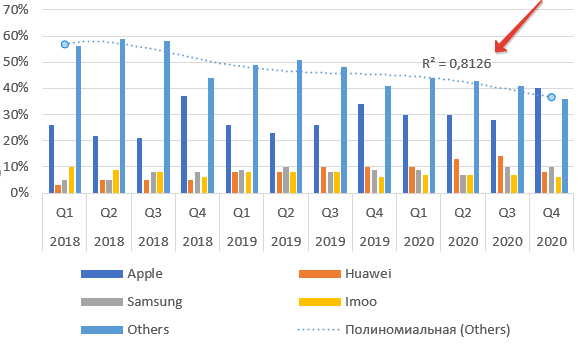
Для примера возьмем данные о продажах умных часов по брендам. Саму таблицу и график можно найти по этой ссылке на сайте CounterPointResearch. Там много подобной информации.
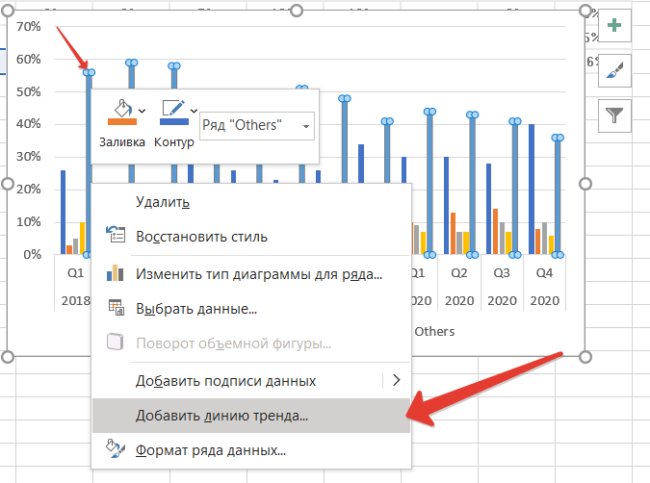
Выделяем диапазон данных и добавляем диаграмму. Теперь наводим мышь на столбцы бренда Others — «остальные», нажимаем правую клавишу мыши. Выбираем пункт Добавить линию тренда.
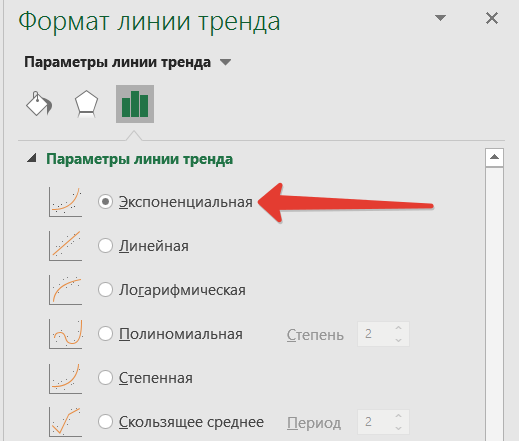
По умолчанию тренд линейный. Чуть позднее расскажу, как выбрать иную функцию, и стоит ли это делать. Теперь подводим курсор мыши к тренду и снова нажимаем правую кнопку.
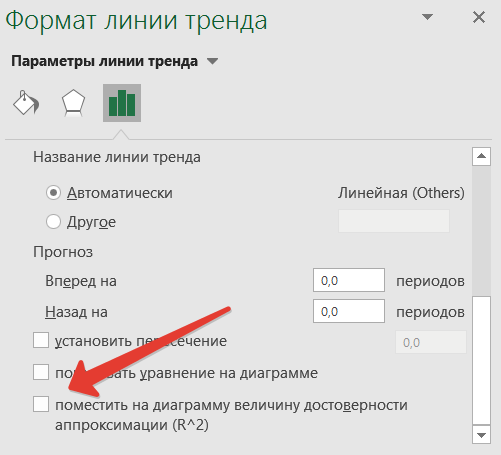
Добавляем на график R².
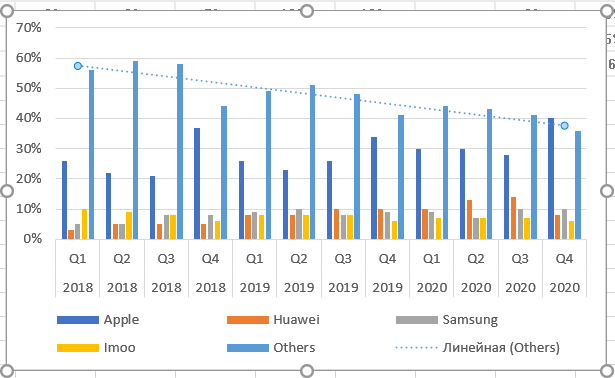
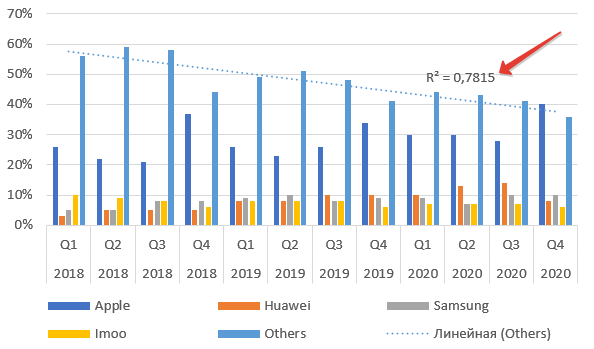
Как видим из названия пункта, это величина достоверности апроксимации. Максимальное значение параметра Р-квадрат единица. Но получить ее можно только на специально подогнанных данных в реальной жизни приемлемое значение 0,8-0,9. В нашем случае — 0,78, что неплохо.
Видео:Excel. Линия трендаСкачать

Стоит ли добиваться максимального значения R²
Улучшить достоверность апроксимации можно меняя вид кривой. Это можно сделать в открывающемся справа окошке Формат линии тренда.
Если использовать полиноминальную функцию, то апроксимацию можно улучшить значительно. Но вот смысла это не имеет. Экономические показатели обычно укладываются в линейный (рост/падение) или экспоненциальный тренд. Экспоненциально, например, растет число клиентов быстрорастущей фирмы.
Выбор полиноминальной функции может и улучшит показатель достоверности, а вот прогноз сделает менее точным.
Видео:Прогнозирование в Excel с помощью линий трендаСкачать

Как использовать тренд для прогноза
Кроме определения общего положения дел (рост/снижение), тренд может предсказать значения показателей в будущем. Это делается в окошке Формата линии тренда.
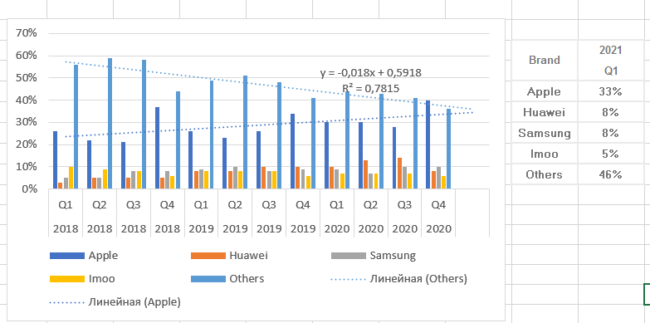
Попробуем предсказать продажи умных часов в первом квартале 2021 году и сравним их с фактом. Добавим два линейных тренда для Apple и Остальных.
Как видим, по яблочным часа прогноз построен верно, по остальным функция прогнозирует значение около 35%, а в реальности 46%. Возможно, это связано с выходом новых игроков на рынок или снижением доли Huawei. Мы имеем дело с относительными показателями (доля), а не с натуральными. Кстати, полиноминальный прогноз для категории Остальные дал бы еще менее точный прогноз, хотя R² и выше, что подтверждает необходимость осторожно выбирать функцию.
Почитайте и другие статьи про работу с таблицами Excel на нашем сайте. Например, у нас есть полезный материал об условном оформлении ячеек в таблице.
Видео:Построить график функции в Excel. Табуляция, линия тренда, уравнение тренда. Часть 1.Скачать

Excel расчет линии тренда
Для наглядной иллюстрации тенденций изменения цены применяется линия тренда. Элемент технического анализа представляет собой геометрическое изображение средних значений анализируемого показателя.
Рассмотрим, как добавить линию тренда на график в Excel.
Видео:Уравнение трендаСкачать

Добавление линии тренда на график
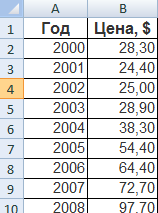
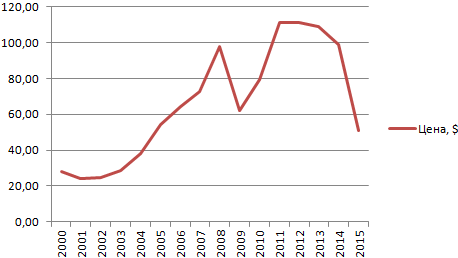
Для примера возьмем средние цены на нефть с 2000 года из открытых источников. Данные для анализа внесем в таблицу:
- Построим на основе таблицы график. Выделим диапазон – перейдем на вкладку «Вставка». Из предложенных типов диаграмм выберем простой график. По горизонтали – год, по вертикали – цена.
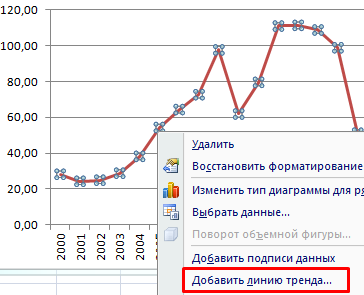
- Щелкаем правой кнопкой мыши по самому графику. Нажимаем «Добавить линию тренда».
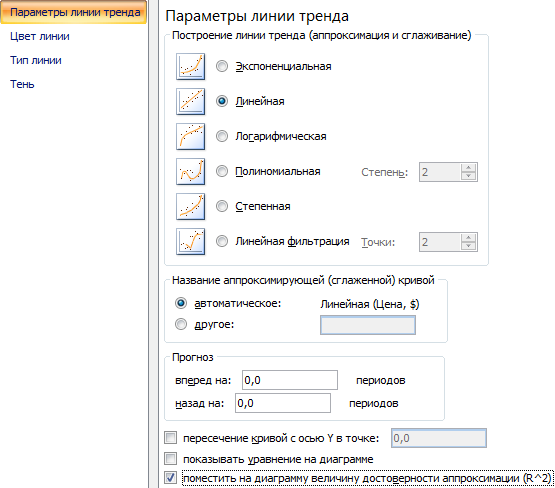
- Открывается окно для настройки параметров линии. Выберем линейный тип и поместим на график величину достоверности аппроксимации.
- На графике появляется косая линия.
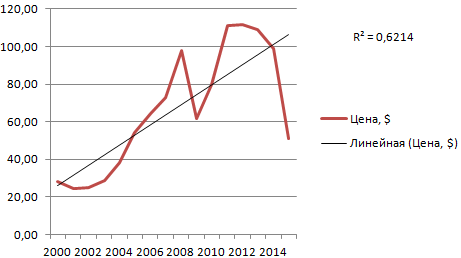
Линия тренда в Excel – это график аппроксимирующей функции. Для чего он нужен – для составления прогнозов на основе статистических данных. С этой целью необходимо продлить линию и определить ее значения.
Если R2 = 1, то ошибка аппроксимации равняется нулю. В нашем примере выбор линейной аппроксимации дал низкую достоверность и плохой результат. Прогноз будет неточным.
Внимание. Линию тренда нельзя добавить следующим типам графиков и диаграмм:
- лепестковый;
- круговой;
- поверхностный;
- кольцевой;
- объемный;
- с накоплением.
Видео:работа с уравнением линии тренда ExcelСкачать

Уравнение линии тренда в Excel
В предложенном выше примере была выбрана линейная аппроксимация только для иллюстрации алгоритма. Как показала величина достоверности, выбор был не совсем удачным.
Следует выбирать тот тип отображения, который наиболее точно проиллюстрирует тенденцию изменений вводимых пользователем данных. Разберемся с вариантами.
Линейная аппроксимация
Ее геометрическое изображение – прямая. Следовательно, линейная аппроксимация применяется для иллюстрации показателя, который растет или уменьшается с постоянной скоростью.
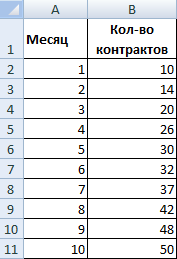
Рассмотрим условное количество заключенных менеджером контрактов на протяжении 10 месяцев:
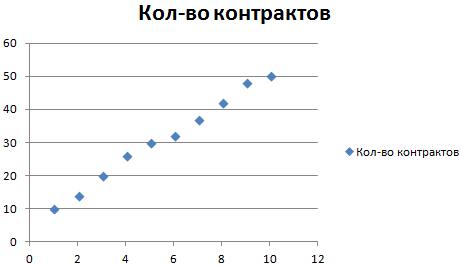
На основании данных в таблице Excel построим точечную диаграмму (она поможет проиллюстрировать линейный тип):
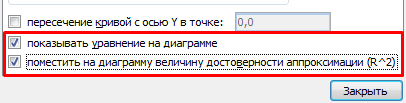
Выделяем диаграмму – «добавить линию тренда». В параметрах выбираем линейный тип. Добавляем величину достоверности аппроксимации и уравнение линии тренда в Excel (достаточно просто поставить галочки внизу окна «Параметры»).
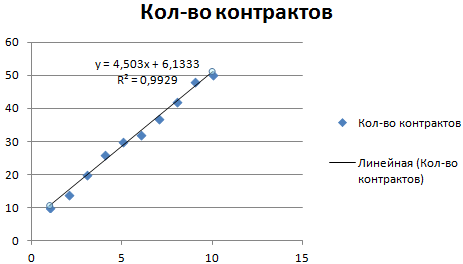
Обратите внимание! При линейном типе аппроксимации точки данных расположены максимально близко к прямой. Данный вид использует следующее уравнение:
y = 4,503x + 6,1333
- где 4,503 – показатель наклона;
- 6,1333 – смещения;
- y – последовательность значений,
- х – номер периода.
Прямая линия на графике отображает стабильный рост качества работы менеджера. Величина достоверности аппроксимации равняется 0,9929, что указывает на хорошее совпадение расчетной прямой с исходными данными. Прогнозы должны получиться точными.
Чтобы спрогнозировать количество заключенных контрактов, например, в 11 периоде, нужно подставить в уравнение число 11 вместо х. В ходе расчетов узнаем, что в 11 периоде этот менеджер заключит 55-56 контрактов.
Экспоненциальная линия тренда
Данный тип будет полезен, если вводимые значения меняются с непрерывно возрастающей скоростью. Экспоненциальная аппроксимация не применяется при наличии нулевых или отрицательных характеристик.
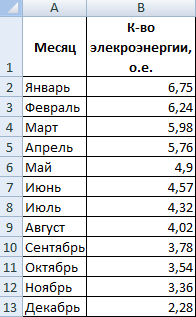
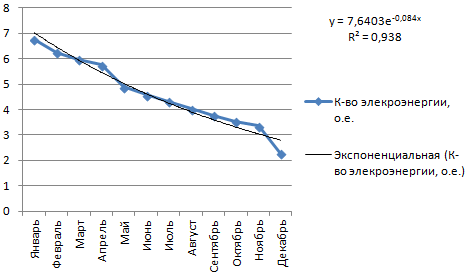
Построим экспоненциальную линию тренда в Excel. Возьмем для примера условные значения полезного отпуска электроэнергии в регионе Х:
Строим график. Добавляем экспоненциальную линию.
Уравнение имеет следующий вид:
- где 7,6403 и -0,084 – константы;
- е – основание натурального логарифма.
Показатель величины достоверности аппроксимации составил 0,938 – кривая соответствует данным, ошибка минимальна, прогнозы будут точными.
Логарифмическая линия тренда в Excel
Используется при следующих изменениях показателя: сначала быстрый рост или убывание, потом – относительная стабильность. Оптимизированная кривая хорошо адаптируется к подобному «поведению» величины. Логарифмический тренд подходит для прогнозирования продаж нового товара, который только вводится на рынок.
На начальном этапе задача производителя – увеличение клиентской базы. Когда у товара будет свой покупатель, его нужно удержать, обслужить.
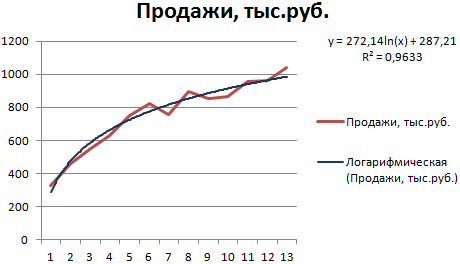
Построим график и добавим логарифмическую линию тренда для прогноза продаж условного продукта:
R2 близок по значению к 1 (0,9633), что указывает на минимальную ошибку аппроксимации. Спрогнозируем объемы продаж в последующие периоды. Для этого нужно в уравнение вместо х подставлять номер периода.
| Период | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Прогноз | 1005,4 | 1024,18 | 1041,74 | 1058,24 | 1073,8 | 1088,51 | 1102,47 |
Для расчета прогнозных цифр использовалась формула вида: =272,14*LN(B18)+287,21. Где В18 – номер периода.
Полиномиальная линия тренда в Excel
Данной кривой свойственны переменные возрастание и убывание. Для полиномов (многочленов) определяется степень (по количеству максимальных и минимальных величин). К примеру, один экстремум (минимум и максимум) – это вторая степень, два экстремума – третья степень, три – четвертая.
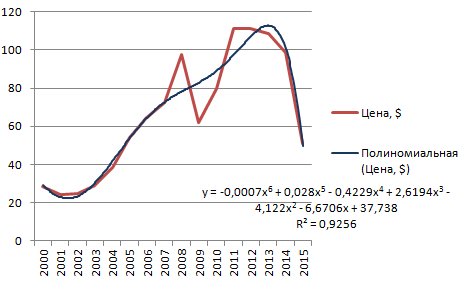
Полиномиальный тренд в Excel применяется для анализа большого набора данных о нестабильной величине. Посмотрим на примере первого набора значений (цены на нефть).
Чтобы получить такую величину достоверности аппроксимации (0,9256), пришлось поставить 6 степень.
Зато такой тренд позволяет составлять более-менее точные прогнозы.
Прогнозирование – это очень важный элемент практически любой сферы деятельности, начиная от экономики и заканчивая инженерией. Существует большое количество программного обеспечения, специализирующегося именно на этом направлении. К сожалению, далеко не все пользователи знают, что обычный табличный процессор Excel имеет в своем арсенале инструменты для выполнения прогнозирования, которые по своей эффективности мало чем уступают профессиональным программам. Давайте выясним, что это за инструменты, и как сделать прогноз на практике.
Видео:LibreOffice Calc. Урок 25. Линия тренда в диаграммах. | Работа с таблицамиСкачать

Процедура прогнозирования
Целью любого прогнозирования является выявление текущей тенденции, и определение предполагаемого результата в отношении изучаемого объекта на определенный момент времени в будущем.
Способ 1: линия тренда
Одним из самых популярных видов графического прогнозирования в Экселе является экстраполяция выполненная построением линии тренда.
Попробуем предсказать сумму прибыли предприятия через 3 года на основе данных по этому показателю за предыдущие 12 лет.
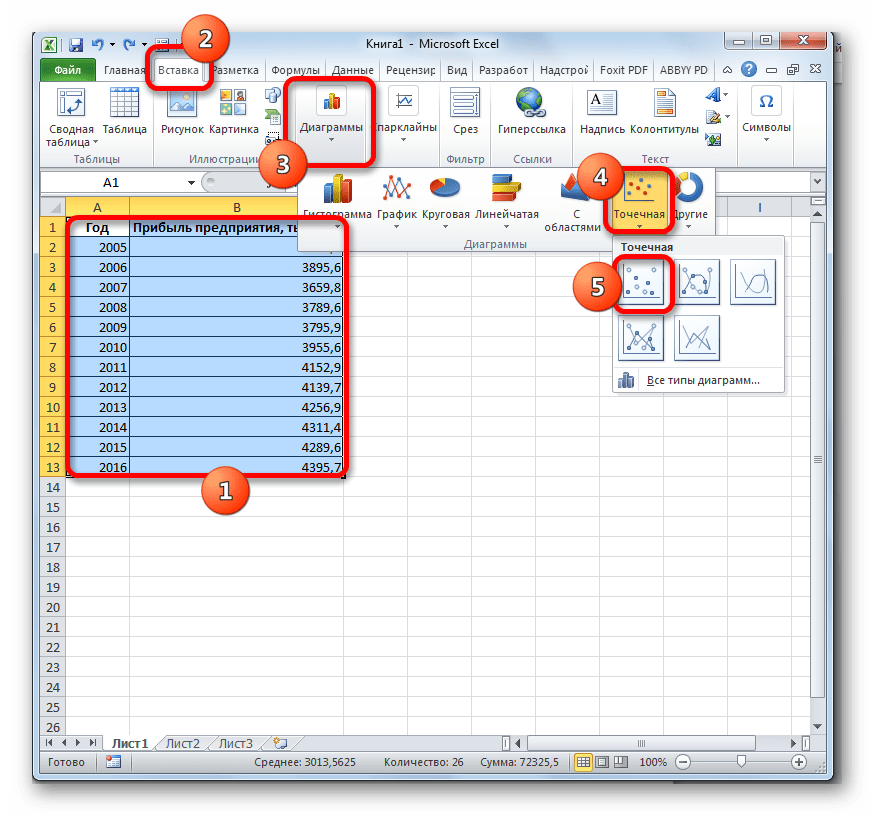
- Строим график зависимости на основе табличных данных, состоящих из аргументов и значений функции. Для этого выделяем табличную область, а затем, находясь во вкладке «Вставка», кликаем по значку нужного вида диаграммы, который находится в блоке «Диаграммы». Затем выбираем подходящий для конкретной ситуации тип. Лучше всего выбрать точечную диаграмму. Можно выбрать и другой вид, но тогда, чтобы данные отображались корректно, придется выполнить редактирование, в частности убрать линию аргумента и выбрать другую шкалу горизонтальной оси.
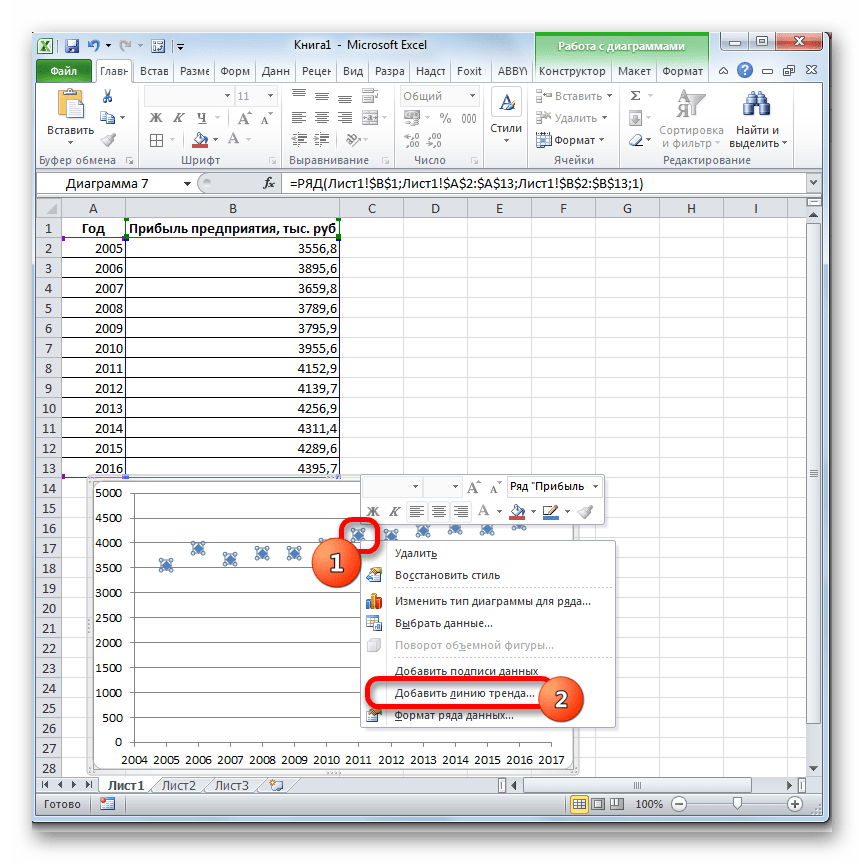
Теперь нам нужно построить линию тренда. Делаем щелчок правой кнопкой мыши по любой из точек диаграммы. В активировавшемся контекстном меню останавливаем выбор на пункте «Добавить линию тренда».
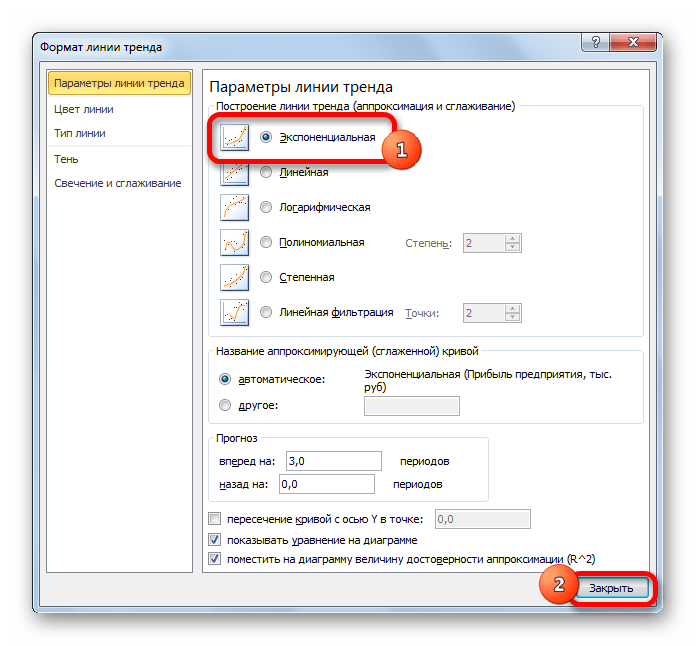
Давайте для начала выберем линейную аппроксимацию.
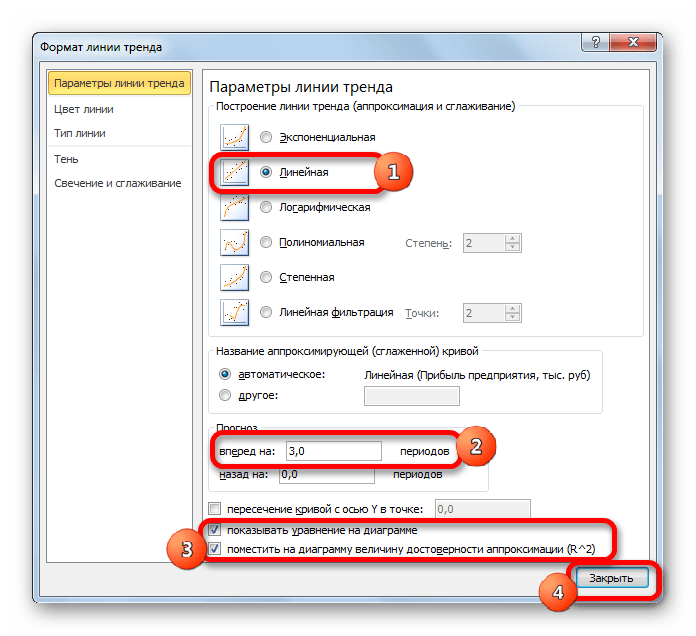
В блоке настроек «Прогноз» в поле «Вперед на» устанавливаем число «3,0», так как нам нужно составить прогноз на три года вперед. Кроме того, можно установить галочки около настроек «Показывать уравнение на диаграмме» и «Поместить на диаграмме величину достоверности аппроксимации (R^2)». Последний показатель отображает качество линии тренда. После того, как настройки произведены, жмем на кнопку «Закрыть».
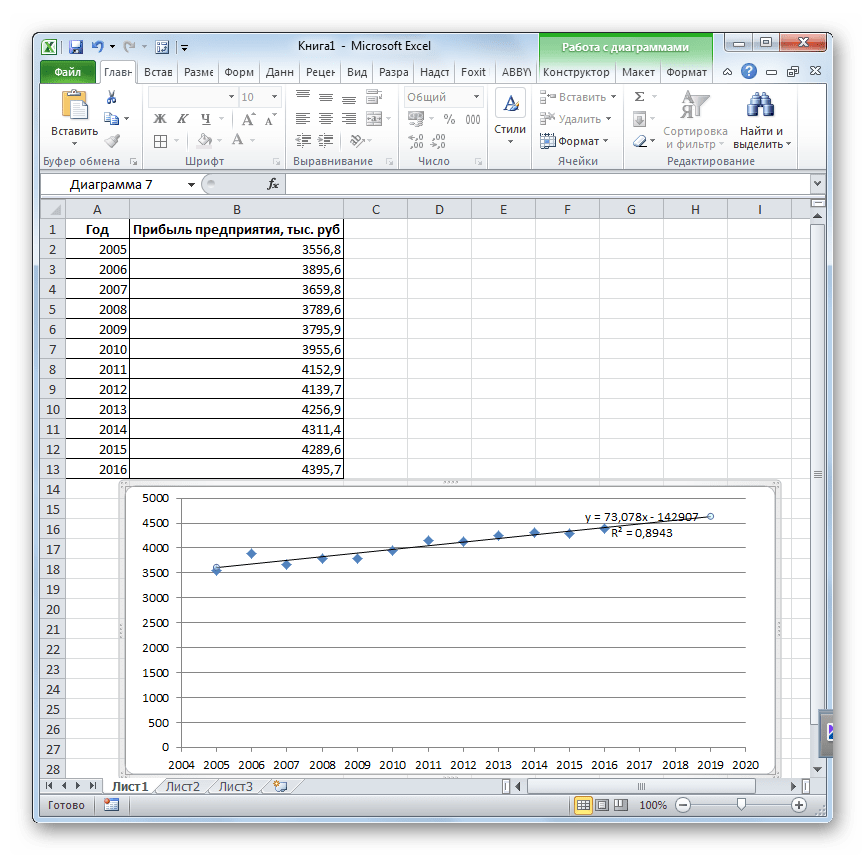
Линия тренда построена и по ней мы можем определить примерную величину прибыли через три года. Как видим, к тому времени она должна перевалить за 4500 тыс. рублей. Коэффициент R2, как уже было сказано выше, отображает качество линии тренда. В нашем случае величина R2 составляет 0,89. Чем выше коэффициент, тем выше достоверность линии. Максимальная величина его может быть равной 1. Принято считать, что при коэффициенте свыше 0,85 линия тренда является достоверной.
Если же вас не устраивает уровень достоверности, то можно вернуться в окно формата линии тренда и выбрать любой другой тип аппроксимации. Можно перепробовать все доступные варианты, чтобы найти наиболее точный.
Нужно заметить, что эффективным прогноз с помощью экстраполяции через линию тренда может быть, если период прогнозирования не превышает 30% от анализируемой базы периодов. То есть, при анализе периода в 12 лет мы не можем составить эффективный прогноз более чем на 3-4 года. Но даже в этом случае он будет относительно достоверным, если за это время не будет никаких форс-мажоров или наоборот чрезвычайно благоприятных обстоятельств, которых не было в предыдущих периодах.
Способ 2: оператор ПРЕДСКАЗ
Экстраполяцию для табличных данных можно произвести через стандартную функцию Эксель ПРЕДСКАЗ. Этот аргумент относится к категории статистических инструментов и имеет следующий синтаксис:
«X» – это аргумент, значение функции для которого нужно определить. В нашем случае в качестве аргумента будет выступать год, на который следует произвести прогнозирование.
«Известные значения y» — база известных значений функции. В нашем случае в её роли выступает величина прибыли за предыдущие периоды.
«Известные значения x» — это аргументы, которым соответствуют известные значения функции. В их роли у нас выступает нумерация годов, за которые была собрана информация о прибыли предыдущих лет.
Естественно, что в качестве аргумента не обязательно должен выступать временной отрезок. Например, им может являться температура, а значением функции может выступать уровень расширения воды при нагревании.
При вычислении данным способом используется метод линейной регрессии.
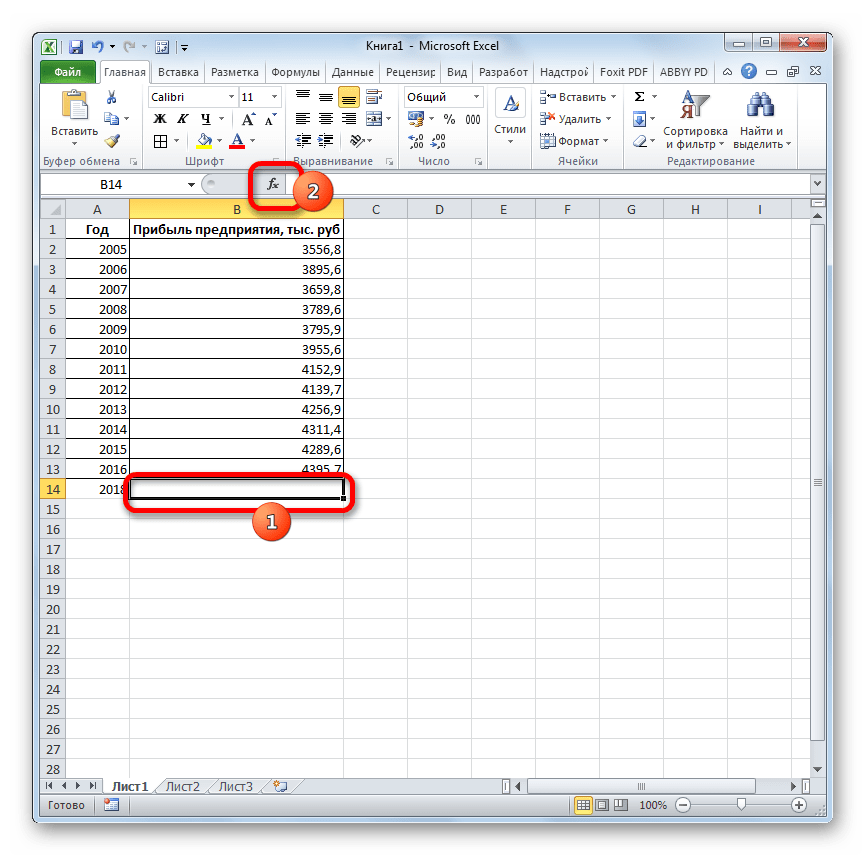
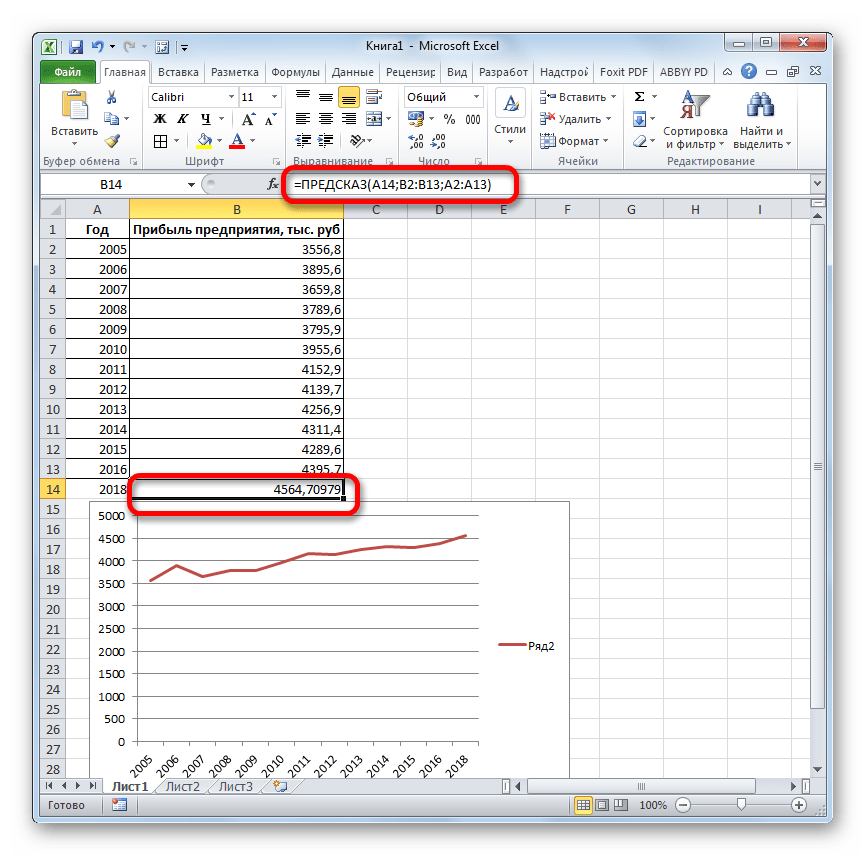
Давайте разберем нюансы применения оператора ПРЕДСКАЗ на конкретном примере. Возьмем всю ту же таблицу. Нам нужно будет узнать прогноз прибыли на 2018 год.
- Выделяем незаполненную ячейку на листе, куда планируется выводить результат обработки. Жмем на кнопку «Вставить функцию».
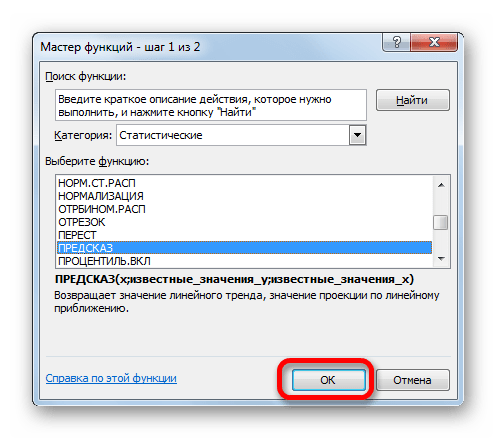
Открывается Мастер функций. В категории «Статистические» выделяем наименование «ПРЕДСКАЗ», а затем щелкаем по кнопке «OK».
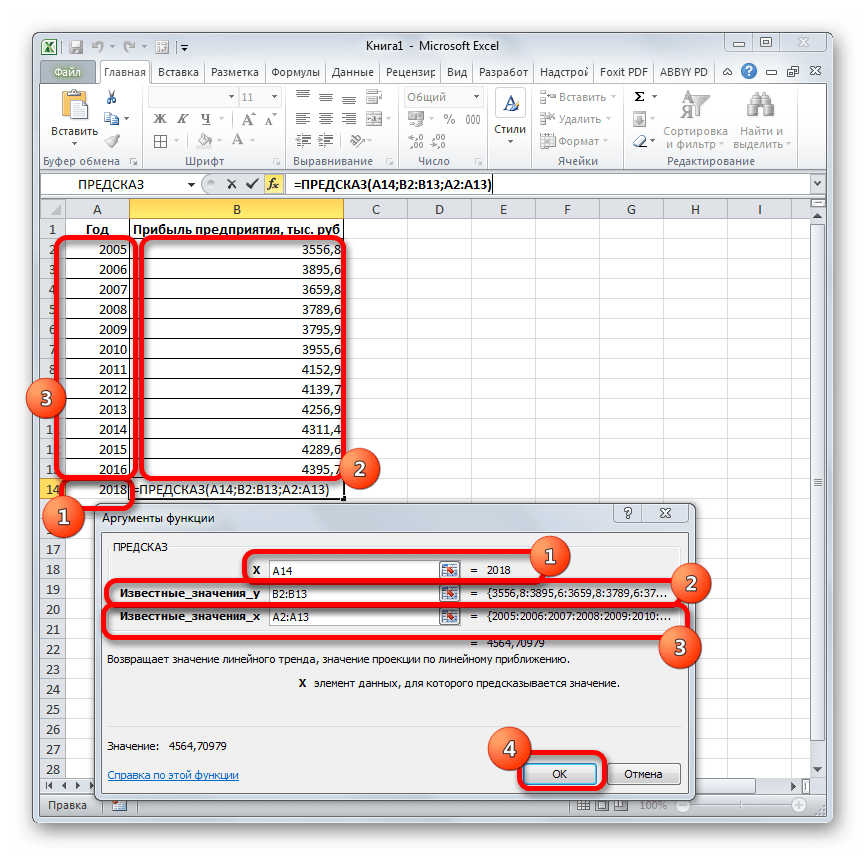
Запускается окно аргументов. В поле «X» указываем величину аргумента, к которому нужно отыскать значение функции. В нашем случаем это 2018 год. Поэтому вносим запись «2018». Но лучше указать этот показатель в ячейке на листе, а в поле «X» просто дать ссылку на него. Это позволит в будущем автоматизировать вычисления и при надобности легко изменять год.
В поле «Известные значения y» указываем координаты столбца «Прибыль предприятия». Это можно сделать, установив курсор в поле, а затем, зажав левую кнопку мыши и выделив соответствующий столбец на листе.
Аналогичным образом в поле «Известные значения x» вносим адрес столбца «Год» с данными за прошедший период.
После того, как вся информация внесена, жмем на кнопку «OK».
Оператор производит расчет на основании введенных данных и выводит результат на экран. На 2018 год планируется прибыль в районе 4564,7 тыс. рублей. На основе полученной таблицы мы можем построить график при помощи инструментов создания диаграммы, о которых шла речь выше.
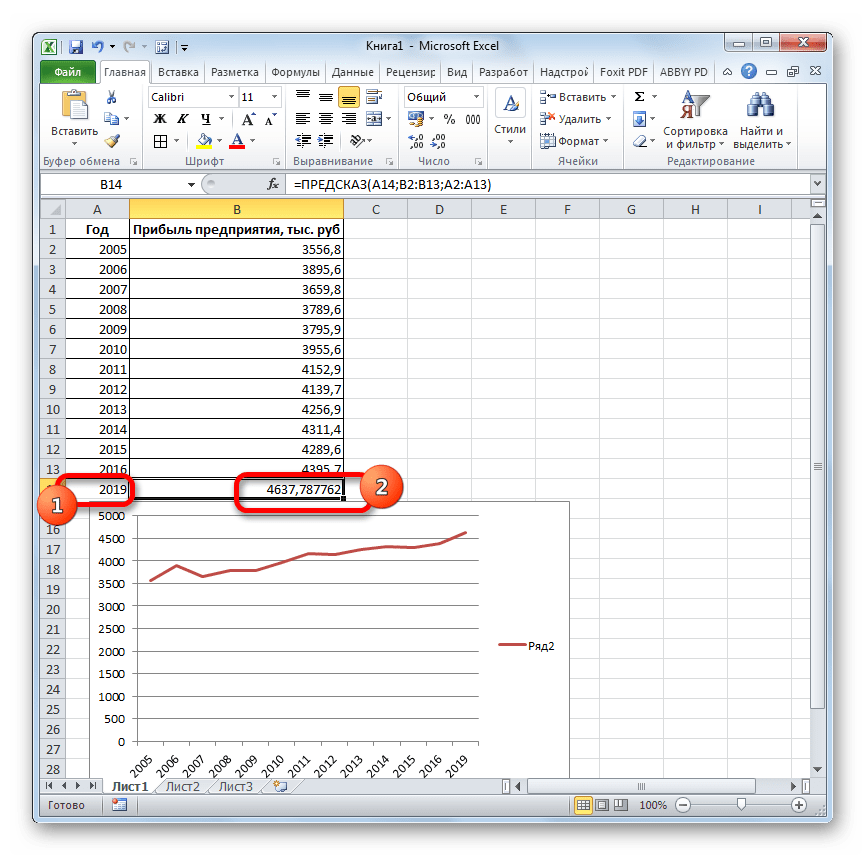
Если поменять год в ячейке, которая использовалась для ввода аргумента, то соответственно изменится результат, а также автоматически обновится график. Например, по прогнозам в 2019 году сумма прибыли составит 4637,8 тыс. рублей.
Но не стоит забывать, что, как и при построении линии тренда, отрезок времени до прогнозируемого периода не должен превышать 30% от всего срока, за который накапливалась база данных.
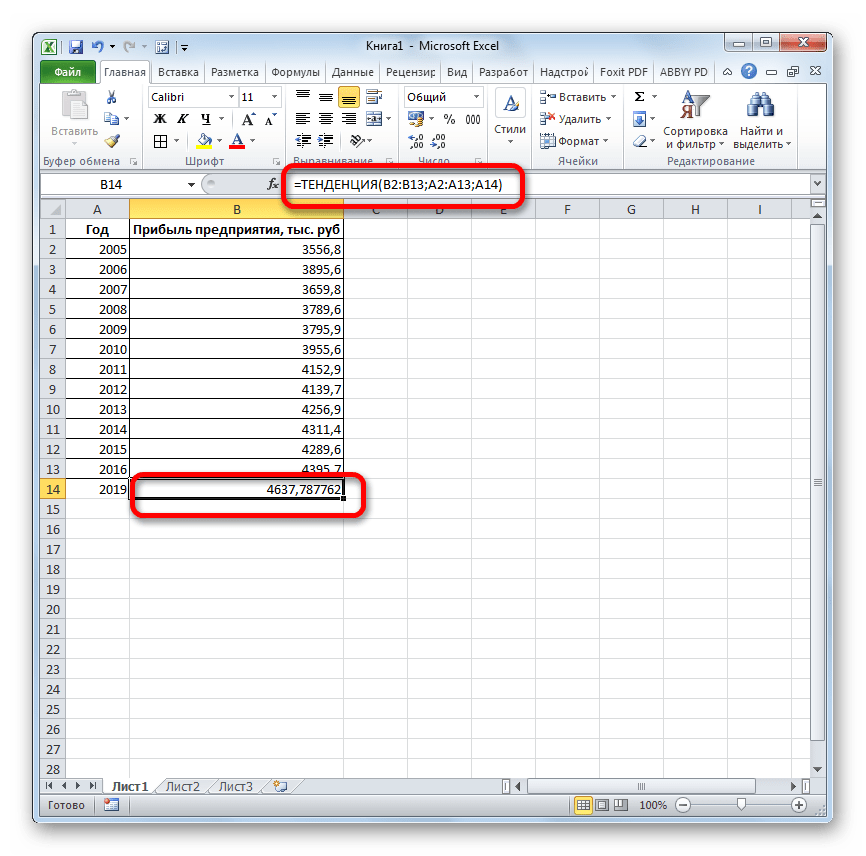
Способ 3: оператор ТЕНДЕНЦИЯ
Для прогнозирования можно использовать ещё одну функцию – ТЕНДЕНЦИЯ. Она также относится к категории статистических операторов. Её синтаксис во многом напоминает синтаксис инструмента ПРЕДСКАЗ и выглядит следующим образом:
=ТЕНДЕНЦИЯ(Известные значения_y;известные значения_x; новые_значения_x;[конст])
Как видим, аргументы «Известные значения y» и «Известные значения x» полностью соответствуют аналогичным элементам оператора ПРЕДСКАЗ, а аргумент «Новые значения x» соответствует аргументу «X» предыдущего инструмента. Кроме того, у ТЕНДЕНЦИЯ имеется дополнительный аргумент «Константа», но он не является обязательным и используется только при наличии постоянных факторов.
Данный оператор наиболее эффективно используется при наличии линейной зависимости функции.
Посмотрим, как этот инструмент будет работать все с тем же массивом данных. Чтобы сравнить полученные результаты, точкой прогнозирования определим 2019 год.
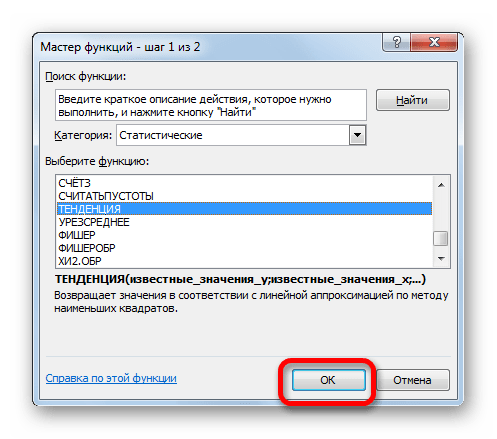
- Производим обозначение ячейки для вывода результата и запускаем Мастер функций обычным способом. В категории «Статистические» находим и выделяем наименование «ТЕНДЕНЦИЯ». Жмем на кнопку «OK».
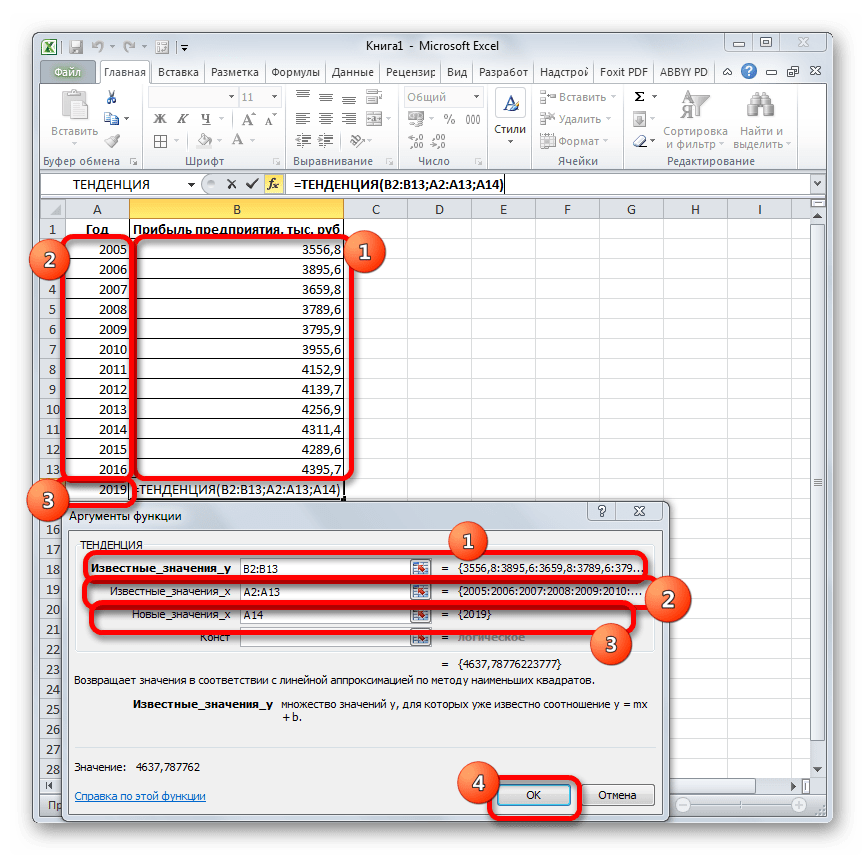
Открывается окно аргументов оператора ТЕНДЕНЦИЯ. В поле «Известные значения y» уже описанным выше способом заносим координаты колонки «Прибыль предприятия». В поле «Известные значения x» вводим адрес столбца «Год». В поле «Новые значения x» заносим ссылку на ячейку, где находится номер года, на который нужно указать прогноз. В нашем случае это 2019 год. Поле «Константа» оставляем пустым. Щелкаем по кнопке «OK».
Оператор обрабатывает данные и выводит результат на экран. Как видим, сумма прогнозируемой прибыли на 2019 год, рассчитанная методом линейной зависимости, составит, как и при предыдущем методе расчета, 4637,8 тыс. рублей.
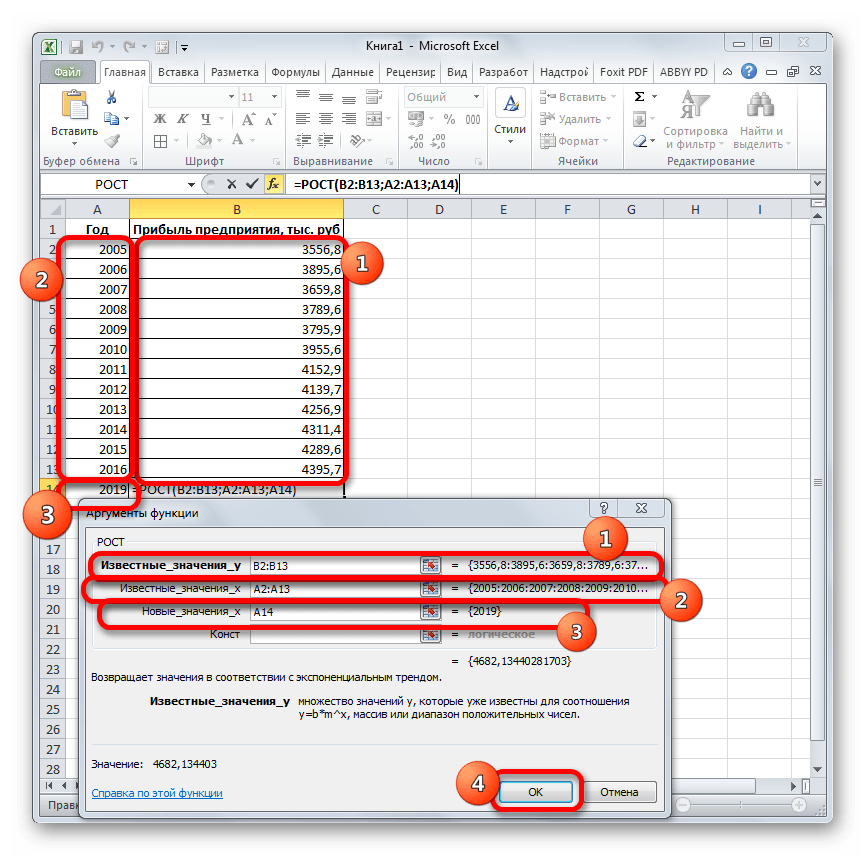
Способ 4: оператор РОСТ
Ещё одной функцией, с помощью которой можно производить прогнозирование в Экселе, является оператор РОСТ. Он тоже относится к статистической группе инструментов, но, в отличие от предыдущих, при расчете применяет не метод линейной зависимости, а экспоненциальной. Синтаксис этого инструмента выглядит таким образом:
=РОСТ(Известные значения_y;известные значения_x; новые_значения_x;[конст])
Как видим, аргументы у данной функции в точности повторяют аргументы оператора ТЕНДЕНЦИЯ, так что второй раз на их описании останавливаться не будем, а сразу перейдем к применению этого инструмента на практике.
- Выделяем ячейку вывода результата и уже привычным путем вызываем Мастер функций. В списке статистических операторов ищем пункт «РОСТ», выделяем его и щелкаем по кнопке «OK».
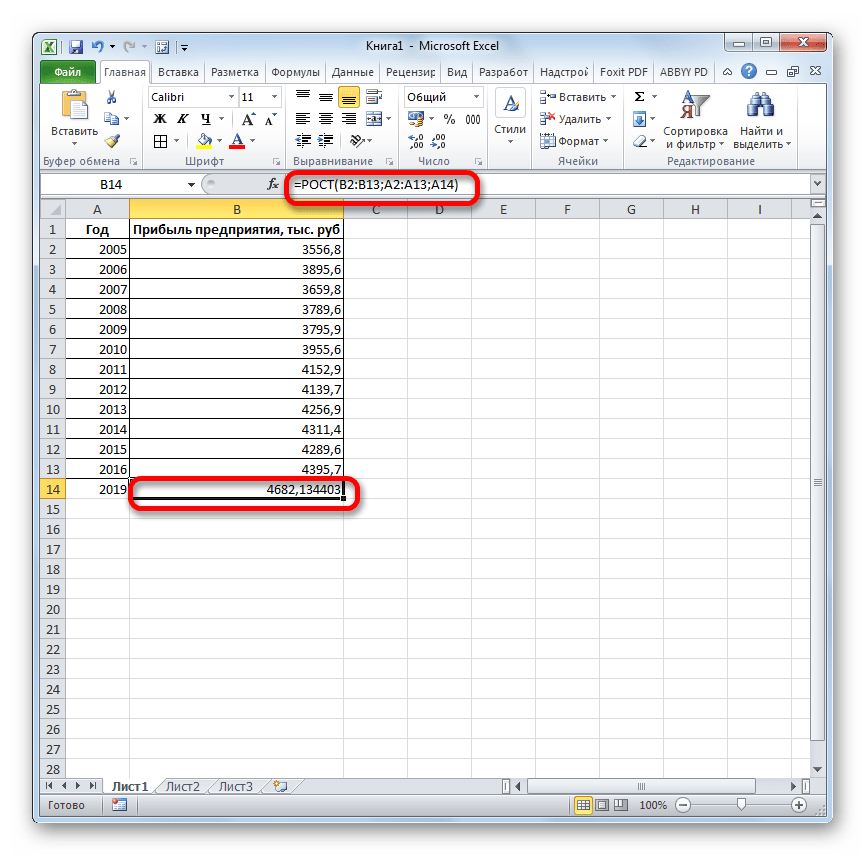
Происходит активация окна аргументов указанной выше функции. Вводим в поля этого окна данные полностью аналогично тому, как мы их вводили в окне аргументов оператора ТЕНДЕНЦИЯ. После того, как информация внесена, жмем на кнопку «OK».
Результат обработки данных выводится на монитор в указанной ранее ячейке. Как видим, на этот раз результат составляет 4682,1 тыс. рублей. Отличия от результатов обработки данных оператором ТЕНДЕНЦИЯ незначительны, но они имеются. Это связано с тем, что данные инструменты применяют разные методы расчета: метод линейной зависимости и метод экспоненциальной зависимости.
Способ 5: оператор ЛИНЕЙН
Оператор ЛИНЕЙН при вычислении использует метод линейного приближения. Его не стоит путать с методом линейной зависимости, используемым инструментом ТЕНДЕНЦИЯ. Его синтаксис имеет такой вид:
=ЛИНЕЙН(Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])
Последние два аргумента являются необязательными. С первыми же двумя мы знакомы по предыдущим способам. Но вы, наверное, заметили, что в этой функции отсутствует аргумент, указывающий на новые значения. Дело в том, что данный инструмент определяет только изменение величины выручки за единицу периода, который в нашем случае равен одному году, а вот общий итог нам предстоит подсчитать отдельно, прибавив к последнему фактическому значению прибыли результат вычисления оператора ЛИНЕЙН, умноженный на количество лет.
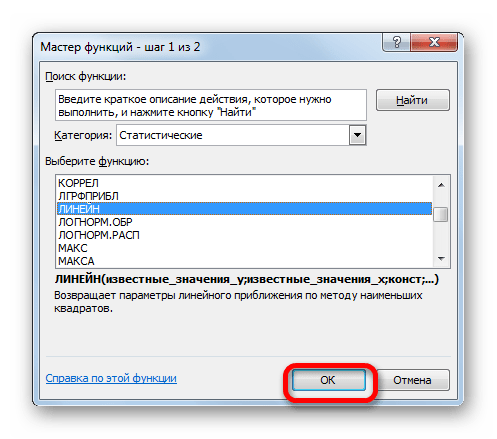
- Производим выделение ячейки, в которой будет производиться вычисление и запускаем Мастер функций. Выделяем наименование «ЛИНЕЙН» в категории «Статистические» и жмем на кнопку «OK».
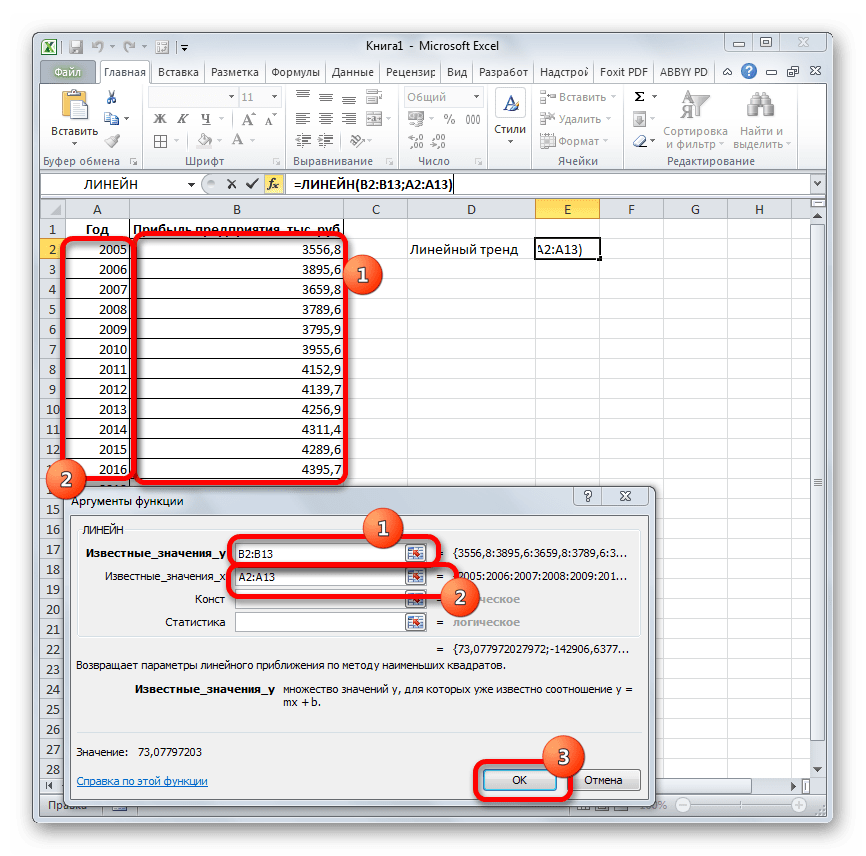
В поле «Известные значения y», открывшегося окна аргументов, вводим координаты столбца «Прибыль предприятия». В поле «Известные значения x» вносим адрес колонки «Год». Остальные поля оставляем пустыми. Затем жмем на кнопку «OK».
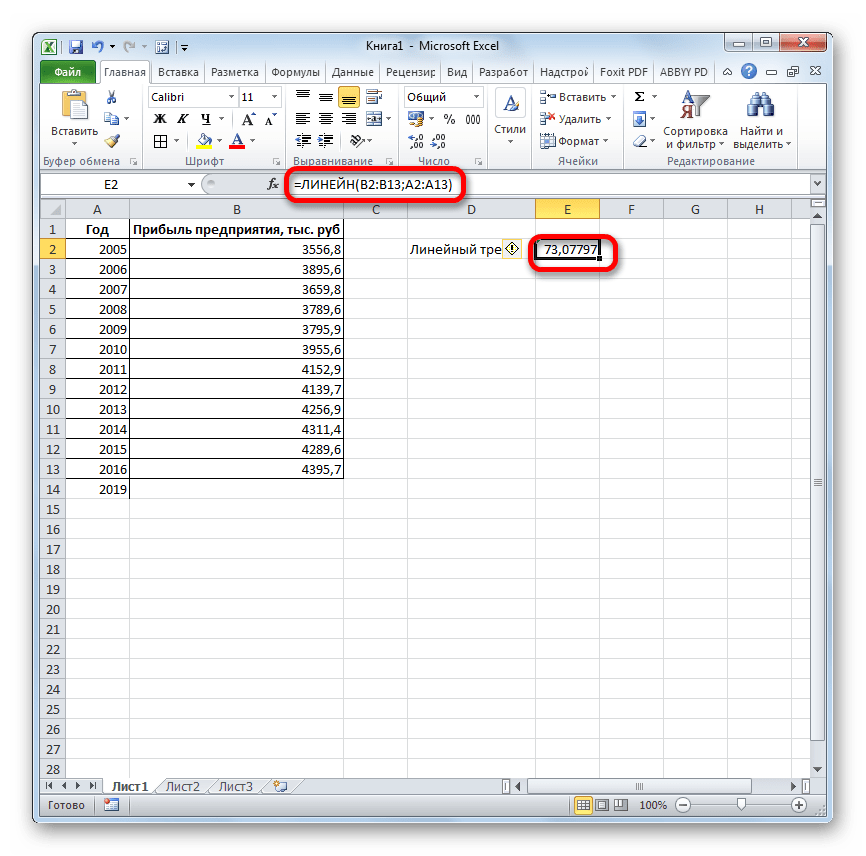
Программа рассчитывает и выводит в выбранную ячейку значение линейного тренда.
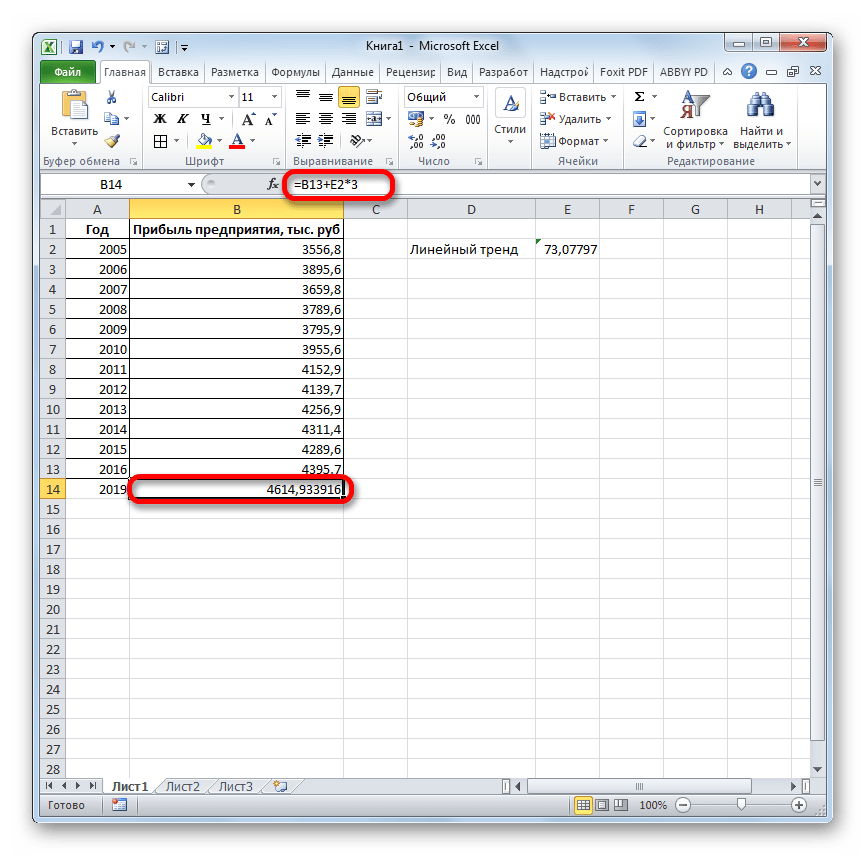
Теперь нам предстоит выяснить величину прогнозируемой прибыли на 2019 год. Устанавливаем знак «=» в любую пустую ячейку на листе. Кликаем по ячейке, в которой содержится фактическая величина прибыли за последний изучаемый год (2016 г.). Ставим знак «+». Далее кликаем по ячейке, в которой содержится рассчитанный ранее линейный тренд. Ставим знак «*». Так как между последним годом изучаемого периода (2016 г.) и годом на который нужно сделать прогноз (2019 г.) лежит срок в три года, то устанавливаем в ячейке число «3». Чтобы произвести расчет кликаем по кнопке Enter.
Как видим, прогнозируемая величина прибыли, рассчитанная методом линейного приближения, в 2019 году составит 4614,9 тыс. рублей.
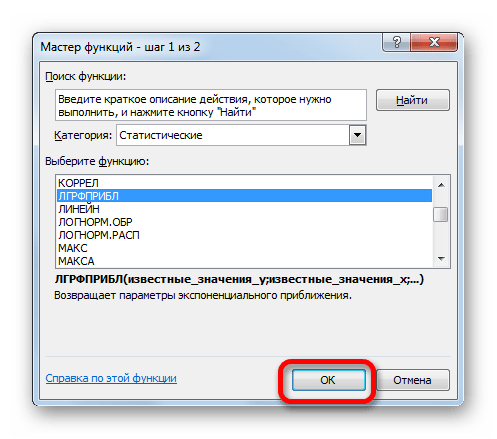
Способ 6: оператор ЛГРФПРИБЛ
Последний инструмент, который мы рассмотрим, будет ЛГРФПРИБЛ. Этот оператор производит расчеты на основе метода экспоненциального приближения. Его синтаксис имеет следующую структуру:
= ЛГРФПРИБЛ (Известные значения_y;известные значения_x; новые_значения_x;[конст];[статистика])
Как видим, все аргументы полностью повторяют соответствующие элементы предыдущей функции. Алгоритм расчета прогноза немного изменится. Функция рассчитает экспоненциальный тренд, который покажет, во сколько раз поменяется сумма выручки за один период, то есть, за год. Нам нужно будет найти разницу в прибыли между последним фактическим периодом и первым плановым, умножить её на число плановых периодов (3) и прибавить к результату сумму последнего фактического периода.
- В списке операторов Мастера функций выделяем наименование «ЛГРФПРИБЛ». Делаем щелчок по кнопке «OK».
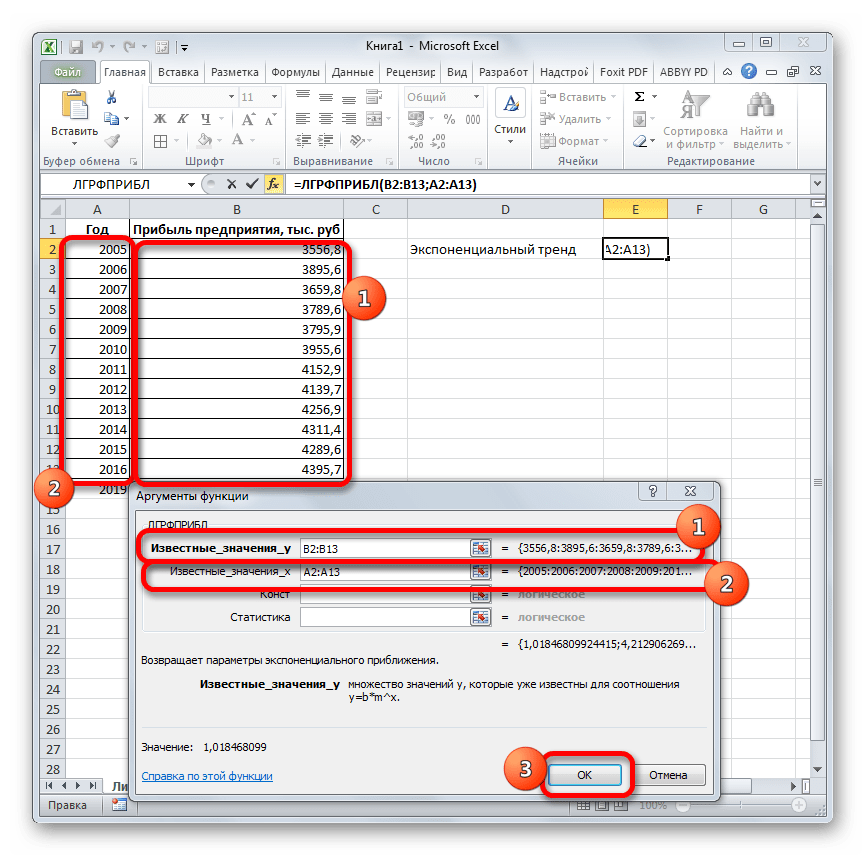
Запускается окно аргументов. В нем вносим данные точно так, как это делали, применяя функцию ЛИНЕЙН. Щелкаем по кнопке «OK».
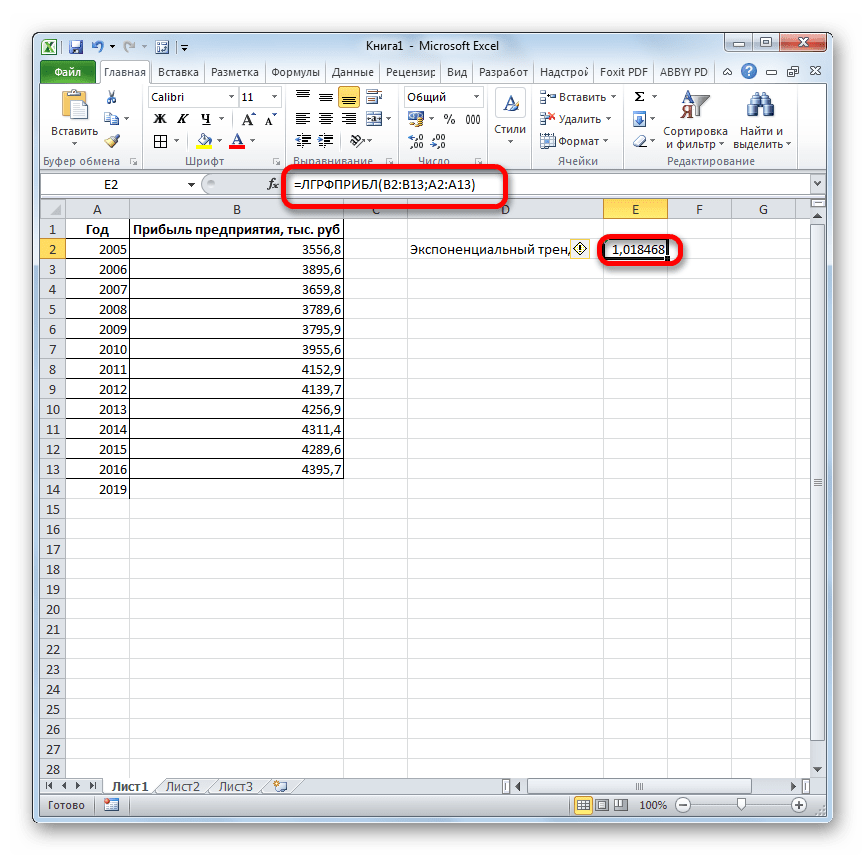
Результат экспоненциального тренда подсчитан и выведен в обозначенную ячейку.
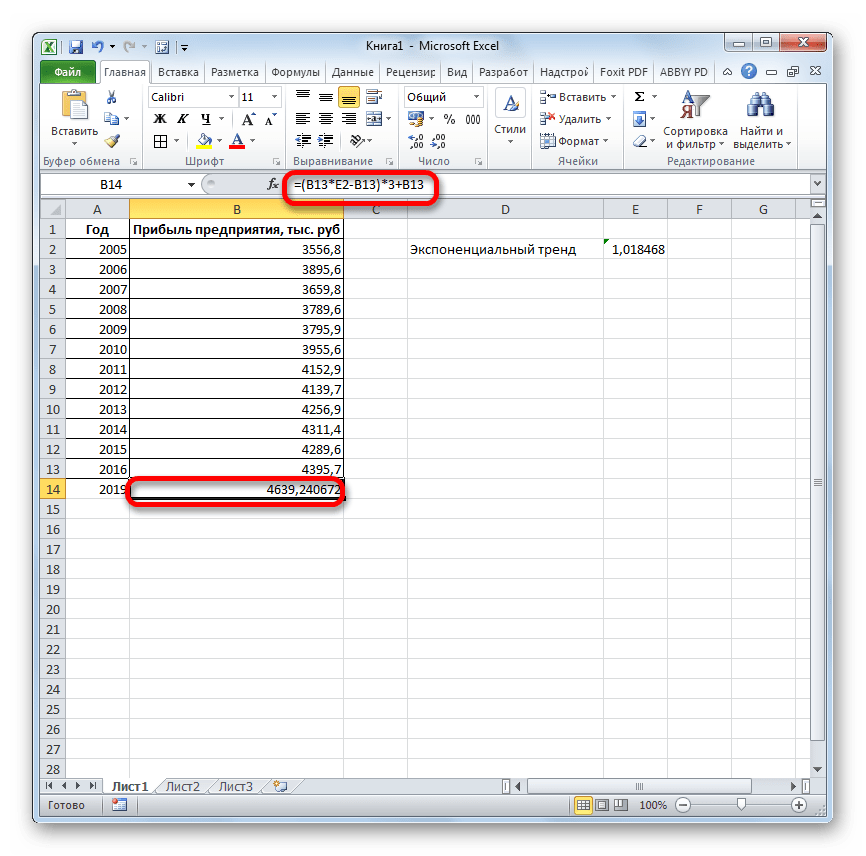
Ставим знак «=» в пустую ячейку. Открываем скобки и выделяем ячейку, которая содержит значение выручки за последний фактический период. Ставим знак «*» и выделяем ячейку, содержащую экспоненциальный тренд. Ставим знак минус и снова кликаем по элементу, в котором находится величина выручки за последний период. Закрываем скобку и вбиваем символы «*3+» без кавычек. Снова кликаем по той же ячейке, которую выделяли в последний раз. Для проведения расчета жмем на кнопку Enter.
Прогнозируемая сумма прибыли в 2019 году, которая была рассчитана методом экспоненциального приближения, составит 4639,2 тыс. рублей, что опять не сильно отличается от результатов, полученных при вычислении предыдущими способами.
Мы выяснили, какими способами можно произвести прогнозирование в программе Эксель. Графическим путем это можно сделать через применение линии тренда, а аналитическим – используя целый ряд встроенных статистических функций. В результате обработки идентичных данных этими операторами может получиться разный итог. Но это не удивительно, так как все они используют разные методы расчета. Если колебание небольшое, то все эти варианты, применимые к конкретному случаю, можно считать относительно достоверными.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Это первая статья из серии «Как самостоятельно рассчитать прогноз продаж с учетом роста и сезонности», из которой вы узнаете о 5 способах расчета значений линейного тренда в Excel.
Для того, чтобы легче было научиться прогнозировать продажи с учетом роста и сезонности, я разбил 1 большую статью о расчете прогноза на 3 части:
- Расчет значений тренда (рассмотрим на примере Линейного тренда в этой статье);
- Расчет сезонности;
- Расчет прогноза;
После изучения данного материала вы сможете выбрать оптимальный способ расчета значений линейного тренда, который будет удобен для решения вашей задачи, а в последствии, и для расчета прогноза наиболее удобным для вас способом.
Линейный тренд хорошо применять для временного ряда, данные которого увеличиваются или убывают с постоянной скоростью.
Рассмотрим линейный тренд на примере расчета прогноза продаж в Excel по месяцам.
Временной ряд продажи по месяцам (см. вложенный файл).
В этом временном ряду у нас есть 2 переменных:
Уравнение линейного тренда y(x)=a+bx, где
y — это объёмы продаж
x — номер периода (порядковый номер месяца)
a – точка пересечения с осью y на графике (минимальный уровень);
b – это значение, на которое увеличивается следующее значение временного ряда;
1-й способ расчета значений линейного тренда в Excel с помощью графика
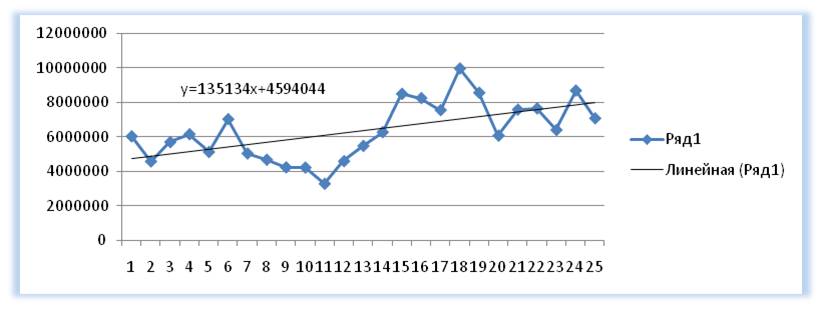
Для прогнозирования нам необходимо рассчитать значения линейного тренда, как для анализируемых значений, так и для будущих периодов.
При расчете значений линейного тренде нам будут известны:
- Время — значение по оси Х;
- Значение «a» и «b» уравнения линейного тренда y(x)=a+bx;
Рассчитываем значения тренда для каждого периода времени от 1 до 25, а также для будущих периодов с 26 месяца до 36.
Например, для 26 месяца значение тренда рассчитывается по следующей схеме: в уравнение подставляем x=26 и получаем y=135134*26+4594044=8107551
27-го y=135134*27+4594044=8242686
2-й способ расчета значений линейного тренда в Excel — функция ЛИНЕЙН
1. Рассчитаем коэффициенты линейного тренда с помощью стандартной функции Excel:
=ЛИНЕЙН(известные значения y, известные значения x, константа, статистика)
Для расчета коэффициентов в формулу вводим
известные значения y (объёмы продаж за периоды),
известные значения x (номера периодов),
вместо константы ставим 1,
вместо статистики 0,
Получаем 135135 — значение (b) линейного тренда y=a+bx;
Для того чтобы Excel рассчитал сразу 2 коэффициента (a) и (b) линейного тренда y=a+bx, необходимо
- установить курсор в ячейку с формулой и выделить соседнюю справа, как на рисунке;
- нажимаем клавишу F2, а затем одновременно — клавиши CTRL + SHIFT + ВВОД.
Получаем 135135, 4594044 — значение (b) и (a) линейного тренда y=a+bx;
2. Рассчитаем значения линейного тренда с помощью полученных коэффициентов . Подставляем в уравнение y=135134*x+4594044 номера периодов — x, для которых хотим рассчитать значения линейного тренда.
2-й способ точнее, чем первый, т.к. коэффициенты тренда мы получаем без округления, а также быстрее.
3-й способ расчета значений линейного тренда в Excel — функция ТЕНДЕНЦИЯ
Рассчитаем значения линейного тренда с помощью стандартной функции Excel:
=ТЕНДЕНЦИЯ(известные значения y; известные значения x; новые значения x; конста)
Подставляем в формулу
- известные значения y — это объёмы продаж за анализируемый период (фиксируем диапазон в формуле, выделяем ссылку и нажимаем F4);
- известные значения x — это номера периодов x для известных значений объёмов продаж y;
- новые значения x — это номера периодов, для которых мы хотим рассчитать значения линейного тренда;
- константа — ставим 1, необходимо для того, чтобы значения тренда рассчитывались с учетом коэффицента (a) для линейного тренда y=a+bx;
Для того чтобы рассчитать значения тренда для всего временного диапазона, в «новые значения x» вводим диапазон значений X, выделяем диапазон ячеек равный диапазону со значениями X с формулой в первой ячейке и нажимаем клавишу F2, а затем — клавиши CTRL + SHIFT + ВВОД.
4-й способ расчета значений линейного тренда в Excel — функция ПРЕДСКАЗ
Рассчитаем значения линейного тренда с помощью стандартной функции Excel:
=ПРЕДСКАЗ(x; известные значения y; известные значения x)
Вместо X поставляем номер периода, для которого рассчитываем значение тренда.
Вместо «известные значения y» — объёмы продаж за анализируемый период (фиксируем диапазон в формуле, выделяем ссылку и нажимаем F4);
«известные значения x» — это номера периодов для каждого выделенного объёма продаж.
3-й и 4-й способ расчета значений линейного тренда быстрее, чем 1 и 2-й, однако с его помощью невозможно управлять коэффициентами тренда, как описано в статье «О линейном тренде».
5-й способ расчета значений линейного тренда в Excel — Forecast4AC PRO
2. Заходим в меню программы и нажимаем «Start_Forecast». Значения линейного тренда рассчитаны.
Для расчета прогноза осталось применить к значениям трендов будущих периодов коэффициенты сезонности, и прогноз продаж с учетом роста и сезонности готов.
В следующих статье «Как самостоятельно сделать прогноз продаж с учетом роста и сезонности» мы:
О том, что еще важно знать о линейном тренде, вы можете узнать в статье «Что важно знать о линейном тренде».
Точных вам прогнозов!
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite — автоматический расчет прогноза в Excel .
- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
Видео:Excel для полных чайников Урок 16 Линия трендаСкачать
Периодические линии тренда в прогнозировании объемов продаж
Недавно мое внимание привлекли две интересные публикации на www.cfin.ru: «Алгоритм прогнозирования объема продаж в MS Excel» С.А. Кошечкина (опубликовано в 2001 г.) и «Доработка алгоритма прогнозирования объема продаж» А.В. Бондаренко (опубликовано в 2004 г.). Авторы проделали замечательную работу, в результате которой читатели могут взять на вооружение простую, практичную и работоспособную методику среднесрочного прогнозирования объемов продаж сезонного товара. Возможности этой методики могут быть существенно расширены, если выйти за рамки ограниченного набора типов линий тренда, предлагаемых «по умолчанию» в MS Excel.
Зачем это нужно? Затем, что выбор линии тренда может быть не просто формальным актом в математических вычислениях. Выделение трендов, коррелирующих с поведением реальных факторов, влияющих на прогнозируемую величину, повышает достоверность прогнозов, делает их более «прозрачными» для понимания. Данная статья показывает, как выбирать и использовать дополнительные типы линий тренда в рамках упомянутой методики.
В качестве примера будем использовать все те же данные об объемах продаж Нижегородского мороженого, приведенные С.А. Кошечкиным. Напомним их:
| № п.п. | Месяц | Объем продаж (руб.) | № п.п. | Месяц | Объем продаж (руб.) |
| 1 | июль | 8174,40 | 13 | июль | |
| 2 | август | 5078,33 | 14 | август | |
| 3 | сентябрь | 4507,20 | 15 | сентябрь | |
| 4 | октябрь | 2257,19 | 16 | октябрь | |
| 5 | ноябрь | 3400,69 | 17 | ноябрь | |
| 6 | декабрь | 2968,71 | 18 | декабрь | |
| 7 | январь | 2147,14 | 19 | январь | |
| 8 | февраль | 1325,56 | 20 | февраль | |
| 9 | март | 2290,95 | 21 | март | |
| 10 | апрель | 2953,34 | 22 | апрель | |
| 11 | май | 4216,28 | 23 | май | |
| 12 | июнь | 8227,569 | 24 | июнь | 9050,3264 |
Полезно взглянуть также и на графическое отображение изменений объемов продаж, которое показано на рис. 1.
Рис. 1.
Напомню поставленную предыдущими авторами задачу: составить прогноз продаж продукции на следующий год по месяцам.
Конечно, если бы автор нашел годовые графики среднемесячных температур в Нижнем Новгороде, данные о числе ненастных дней по месяцам, кривые заболеваемости ОРВИ (что происходило по октябрям в Н.Н., с чем коррелирует наблюдаемый спад продаж?), возможно, что-то еще, то наше прогнозирование пошло бы иным путем. Но в отсутствие этих данных мы можем констатировать лишь одно: налицо нечто, напоминающее периодическую функцию. А периодическая функция может быть представлена в виде суммы гармонических функций или, иначе говоря, рядом Фурье.
Итак, попробуем выделить из наблюдаемого ряда значений синусоидальный тренд с периодом колебания 12 месяцев: 
Здесь Y12 – функция тренда, A12 — смещение синусоиды относительно нуля, B12 — амплитуда синусоиды, C12 имеет смысл начальной фазы колебания, индекс 12 указывает на выбранный нами период изменения функции. Эта функция будет отражать воздействие температурного (погодного) фактора на продажи мороженого.
Для того, чтобы MS Excel помогла нам сделать необходимые вычисления, понадобится активизировать (а, возможно, и доустановить) некоторые надстройки. Зайдите в меню «Сервис» и выберите команду «Надстройки…». В показанном списке надстроек установите флажки напротив «Analysis ToolPak — VBA», «Пакет анализа» и «Поиск решения». Нажмите ОК. Возможно, что MS Excel потребует установочный диск — приготовьте его заранее.
Теперь поручим MS Excel подобрать наилучшие значения A12, B12 и C12. Должен сразу предупредить, что все, описанное ниже, вы можете посмотреть в файле MS Excel Решение_НН_Мороженое.xls, который можно скачать здесь.
Итак, на чистом рабочем листе (назовем его «Шаг 1») в ячейки А3:А26 запишем номера месяцев наблюдения от 1 до 24, а в ячейки В3:В26 — наблюдаемые объемы продаж. Особенность надстройки «Поиск решения» состоит в том, что требуется задать затравочные значения A12, B12 и C12. Значение A12 должно быть близко к среднему значению объема продаж за год; в качестве затравочного значения выберем 4000 и занесем это число в ячейку Н3. B12 — это амплитуда искомой синусоиды, ее затравочное значение определим как «A12 минус минимальное значение объема продаж». Подойдет самая грубая оценка: 3000; занесем это число в ячейку I3. Судя по графику, C12 или начальная фаза приблизительно составляет – 1/4 периода, или – 3 месяца. Запишем – 3 в ячейку J3. В ячейку К3 поместим наш период: 12 (подбирать его мы не будем, но нам удобно, чтобы он фигурировал в этой ячейке). Наш следующий шаг: необходимо уравнение нашей синусоиды записать в виде формулы MS Excel. Для этого в ячейку D3 заносим: =$H$3+$I$3*SIN(2*ПИ()*(A3-$J$3)/$K$3) (все буквы, кроме «ПИ», латинские; ПИ() — это функция русифицированного MS Excel, которая возвращает константу 3,1415926…; в наборе формулы важно не ошибиться! ). Если после ввода формулы в ячейке D3 появится число 6598 (десятичные знаки опущены), то у вас все получилось, и можно автозаполнителем скопировать эту формулу в ячейки D4:D26. Теперь в ячейках Е3:Е26 вычислим отклонения нашей синусоиды от базовой линии прогноза: в Е3 запишем формулу: =B3–D3 , и скопируем ее автозаполнителем в указанный диапазон. В ячейках F3:F26 необходимо рассчитать квадраты отклонений, для чего в F3 запишем: =E3*E3 и скопируем эту формулу ниже автозаполнителем. В ячейке F27 подсчитаем сумму квадратов отклонений: =СУММ(F3:F26).
И вот наступает ответственный момент. Выделив ячейку F27 с подсчитанной суммой квадратов отклонений, в меню «Сервис» выбираем команду «Поиск решения…». В диалоговом окне в поле «Установить целевую ячейку» должно быть указано $F$27. В переключателе «равной» выбираем «минимальному значению», а в поле «Изменяя ячейки» указываем: $H$3:$J$3 . Скриншот этого диалога показан на рис. 2.
Рис.2. Настроенное окно диалога «Поиск решения»
Нажав кнопку «Выполнить», мы получаем в ячейках H3:J3 значения A12=4160, B12=2686 и C12=–2,03, наилучшим образом приближающие нашу синусоиду к базовой линии. Осталось в завершающем диалоге подтвердить сохранение найденного решения.
Полезно вычислить квадрат коэффициента корреляции (коэффициент детерминации R 2 ) полученного тренда с базовым рядом; в ячейку G27 введем формулу: =КВПИРСОН(D3:D26;B3:B26) . У меня получилось 0,696669. Хорошо это или плохо? Насколько значим полученный коэффициент детерминации?
Для оценки значимости коэффициента детерминации воспользуемся t-критерием Стьюдента. Обычно требуется определить фактическое значение критерия 

На рис.3 показаны графики базовой линии прогноза, линии тренда и отклонений.

Рис. 3.
Что можно сказать о поведении отклонений? Не прослеживается ли в них тоже периодичность, но уже с меньшим периодом — 6 месяцев? Есть ли факторы, которые могут с такой периодичностью воздействовать на продажи мороженого? На последний вопрос должны ответить маркетологи. Я же позволю себе пофантазировать… например, рождественские каникулы и летние отпуска, экзаменационные сессии у студентов, каникулы у школьников имеют полугодичные ритмы. Если люди, живущие в полугодичных ритмах, составляют существенную часть сегмента потребителей мороженого, то почему бы этим ритмам не проявиться в колебаниях спроса? Однако при серьезном подходе к прогнозированию я бы рекомендовал воздерживаться от фантазий и задавать побольше вопросов маркетологам. Но мы изучаем метод, и поэтому примем гипотезу о полугодичном периоде в тренде (а иначе что будет предметом нашего дальнейшего рассмотрения?).
Итак, запасайтесь терпением: нам будет необходимо проделать все то же самое, но для периода 6 месяцев: теперь мы отыщем линию тренда 
- Создайте копию листа «Шаг 1», переименуйте эту копию в «Шаг 2».
- В ячейку В3 запишите формулу: =’Шаг 1′!E3 («Е» — латинское!) и автозаполнителем скопируйте ее в ячейки В4:В26; мы сейчас заменили исходный ряд наблюдений разностями, полученными на листе «Шаг 1».
- В ячейке Н3 укажите затравочное значение для A6; подойдет ноль.
- В ячейке I3 укажите затравочное значение для B6; можно начать с 1000.
- В ячейке К3 укажите период: 6.
- В ячейке J3 укажите затравочное значение для C6; подойдет любое число в диапазоне от -3 до 3.
- Выделите ячейку F27 и выполните «Поиск решения».
Результатом будет A6=0,0127, B6=1449 и C6=-1,099; коэффициент детерминации
R 2 =0,66827 > 0,16284. Таким образом, эту корреляцию также следует признать существенной.
На рис.4 показаны графики базовой линии прогноза, суммы трендов 12 и 6 месяцев, отклонений суммы трендов от базовой линии.
Рис. 4.
Что теперь можно сказать об отклонениях? Во-первых, в них по-прежнему можно заметить периодичность. Причем с приблизительно одинаковой значимостью в них обнаруживаются колебания с периодами 3 и 4 месяца. Во-вторых, в них просматривается тенденция постепенного роста. Что ж, мы тоже будем действовать постепенно.
Уже знакомым нам способом выделим в отклонениях колебания с периодом 3 месяца:

Для этого:
- Создадим копию листа «Шаг 2», переименуем эту копию в «Шаг 3».
- В ячейку В3 запишем формулу: =’Шаг 2′!E3 и автозаполнителем скопируем ее в ячейки В4:В26.
- В ячейке Н3 укажем затравочное значение для A3; подойдет ноль.
- В ячейке I3 укажем затравочное значение для B3; можно начать с 1000.
- В ячейке К3 укажем период: 3.
- В ячейке J3 укажем затравочное значение для C6: 0.
- Выделим ячейку F27 и выполним «Поиск решения».
Результатом будет A3=0, B3=608 и C3=–0,566; коэффициент детерминации
R 2 =0,354638 > 0,16284. Таким образом, и эту корреляцию следует признать существенной.
Теперь займемся периодом 4 месяца: 
- Создадим копию листа «Шаг 3», переименуем эту копию в «Шаг 4».
- В ячейку В3 запишем формулу: =’Шаг 3′!E3 и автозаполнителем скопируем ее в ячейки В4:В26.
- В ячейке Н3 укажем затравочное значение для A4: 0.
- В ячейке I3 укажем затравочное значение для B4: 500.
- В ячейке К3 укажем период: 4.
- В ячейке J3 укажем затравочное значение для C4: 0.
- Выделим ячейку F27 и выполним «Поиск решения».
A4=0, B4=543 и C4=-0,168; коэффициент детерминации R 2 =0,438435 > 0,16284. Корреляция существенна.
Вопрос о природе этих периодов адресуем все тем же маркетологам. Фантазии: ритм 4 месяца — это Рождество, Пасха, начало учебного года. Ритм 3 месяца — сдача квартальных отчетов в налоговые инспекции (как тут не наесться мороженым?). Но вернемся к нашим цифрам: на рис.5 показаны графики базовой линии прогноза, суммы всех выделенных периодических трендов и отклонений суммы трендов от базовой линии.
Рис. 5.
Больше статистически значимых периодических трендов в наших наблюдениях выделить не удастся. Но у нас еще остался возрастающий тренд. Какую аппроксимацию выбрать для него? Если величина тренда невелика по сравнению со значениями базового ряда, то лучше всего выбирать линейную аппроксимацию, т.к. какой бы ни была реальная функция тренда, в первом приближении можно ограничиться линейным членом разложения в ряд Тейлора. Итак, ищем аппроксимацию 
- Создадим копию листа «Шаг 4», переименуем эту копию в «Шаг 5».
- В ячейку В3 запишем формулу: =’Шаг 4′!E3 и автозаполнителем скопируем ее в ячейки В4:В26.
- В ячейку Н3 запишем формулу =ОТРЕЗОК(B3:B26;A3:A26) ; с помощью этой формулы рассчитывается величина AL.
- В ячейку I3 запишем формулу =НАКЛОН(B3:B26;A3:A26) ; с помощью этой формулы рассчитывается величина BL.
- В ячейку D3 запишем формулу расчета линейного тренда с полученными параметрами: =H$3+I$3*A3 ; с помощью автозаполнителя скопируем ее в ячейки D4:D26.
Коэффициент детерминации для линейного тренда составляет 0,156414, что меньше 0,16284, таким образом, эта корреляция может быть расценена как несущественная. Но все не так плохо. Мы можем принять этот тренд, если смягчим требования: уменьшим доверительную вероятность с 0,95 всего до 0,94.
На Рис.6.
Далее будем следовать методу Кошечкина-Бондаренко. В соответствии с этим методом рассчитаем «сезонную компоненту», т.е. усредненные по периодам отклонения от модели.
- Создадим копию листа «Шаг 5», переименуем эту копию в «Шаг 6».
- В ячейку В3 запишем формулу: =’Шаг 5′!E3 и автозаполнителем скопируем ее в ячейки В4:В26.
- В ячейку D3 запишем формулу: =(B3+B15)/2 ; с помощью автозаполнителя скопируем ее в ячейки D4:D14.
- В ячейку D15 запишем ту же формулу: =(B3+B15)/2 , и с помощью автозаполнителя скопируем ее в ячейки D16:D26.
- В ячейке D27 рассчитаем сумму сезонной компоненты: за 2 периода она равна 9,66´10 -13 , т.е. практически равна нулю. По Кошечкину-Бондаренко это — признак сезонности.
- Создадим копию листа «Шаг 1», переименуем эту копию в «Шаг 7».
- В ячейку D3 запишем формулу: =’Шаг 1′!D3+’Шаг 2′!D3+’Шаг 3′!D3+’Шаг 4′!D3+’Шаг 5′!D3+’Шаг 6′!D3; с помощью автозаполнителя скопируем ее в ячейки D4:D26.
- В ячейку Q3 запишем формулу расчета относительных квадратов отклонений модели, которые А.В.Бондаренко почему-то называет среднеквадратичными отклонениями: =(E3/D3)*(E3/D3); с помощью автозаполнителя скопируем формулу в ячейки Q4:Q26.
- В ячейку Q27 запишем формулу вычисления среднего относительного квадрата отклонения модели: =СУММ(Q3:Q26)/H27 ; оно равно 0,000597 (сравните с данными в Таблице 8 у А.В. Бондаренко — лучшее значение для линейного тренда составляет 0,0019; таким образом, точность нашей модели по А.В. Бондаренко составляет 99,94%).
- Относительное среднеквадратичное отклонение будет равно корню квадратному из среднего относительного квадрата отклонения; вычислим его в ячейке Р27: =КОРЕНЬ(Q27)
Диаграмма листа «Модель» покажет график нашей модели — см. рис.7. Коэффициент детерминации модели равен 0,99279.
Рис. 7.
К сожалению, наших данных недостаточно, чтобы судить о распределении ошибок модели. Поэтому будем строить доверительные интервалы, лишь уповая на нормальность распределения ошибок. Доверительный интервал для доверительной вероятности a рассчитывается по формулам: 
- В ячейки R3, S3 запишем формулы расчета границ доверительных интервалов: =D3*(1-P$27*I$27/КОРЕНЬ(H$27)) и =D3*(1+P$27*I$27/КОРЕНЬ(H$27)) соответственно; с помощью автозаполнителя скопируем эти формулы в ячейки R4:R26 и S4:S26.
И, наконец, настала пора перейти к собственно прогнозированию на основе построенной модели. Для этого
- На листах «Шаг 1» — «Шаг 7» в ячейках А27:А38 запишем номера периодов с 25 по 36.
- На листах «Шаг 1» — «Шаг 5», «Шаг 7» формулу из ячейки D26 автозаполнителем скопируем в ячейки D27:D38.
- На листе «Шаг 6» в ячейку D27 запишем формулу =(B3+B15)/2 и с помощью автозаполнителя скопируем ее в ячейки D28:D38
- На листе «Шаг 7» формулы из ячеек R26 и S26 автозаполнителем скопируем в ячейки R27:R38 и S27:S38.
Прогнозируемый объем продаж, верхняя и нижняя границы доверительных интервалов находятся в ячейках D27:D38, R27:R38 и S27:S38 листа «Шаг 7» соответственно. Они же представлены в таблице 2.
| № п.п. | Месяц | Прогнозируемый объем продаж (руб.) | Верхняя граница доверительного интервала (руб.); a=0,95 | Нижняя граница доверительного интервала (руб.); a=0,95 |
| 25 | июль | 9030,028 | 9123,176 | 8936,88 |
| 26 | август | 5779,153 | 5838,767 | 5719,539 |
| 27 | сентябрь | 5179,468 | 5232,896 | 5126,04 |
| 28 | октябрь | 2816,958 | 2846,016 | 2787,9 |
| 29 | ноябрь | 4017,633 | 4059,077 | 3976,19 |
| 30 | декабрь | 3564,053 | 3600,818 | 3527,289 |
| 31 | январь | 2701,403 | 2729,269 | 2673,537 |
| 32 | февраль | 1838,748 | 1857,716 | 1819,781 |
| 33 | март | 2852,408 | 2881,832 | 2822,985 |
| 34 | апрель | 3547,913 | 3584,511 | 3511,315 |
| 35 | май | 4874,003 | 4924,28 | 4823,726 |
| 36 | июнь | 9085,856 | 9179,58 | 8992,132 |
В этом месте самое время делать высоконаучные выводы о том, как надо прогнозировать. Но вместо этого автор решил рассказать поучительную историю.
Не далее, как ранней осенью 2006 года автор делал по заказу одного из своих клиентов прогноз продаж женских сумочек на осень/зиму 2006/2007 гг. В распоряжении автора были наблюдения за 5 предшествующих лет. Модель получилась красивой и очень статистически достоверной. Но, как вы наверное уже догадываетесь, прогноз провалился. Да не просто провалился, и даже не с треском провалился, а провалился со свистом и грохотом! А вся штука оказалась в том, что из-за аномально теплой зимы украинские дамы не одели шубки, а проходили зиму в осенних пальто и кардиганах, и им не понадобилось менять сумочки на сугубо зимние! Мораль сей истории такова: пока существенный фактор влияния на спрос ведет себя стабильно, вы можете даже не подозревать о его существовании. И прогнозировать, прогнозировать, прогнозировать… Но у этой «медали» есть и обратная сторона: изучайте факторы влияния на спрос, учитывайте их в математических моделях, и ваши прогнозы будут чаще сбываться. А пример того, как в MS Excel построить модель с практически любой функциональной зависимостью, как раз и дала вам эта статья.
© Интернет-проект «Корпоративный менеджмент», 1998–2021
💥 Видео
22 Добавление линии трендаСкачать

Уроки Excel. Статистические функции. Линия Тренда.Скачать

22 Добавление линии трендаСкачать

Совмещение графиков в MS Excel (построение комбинированного графика)Скачать

Аппроксимация в ExcelСкачать

#MicrosoftExcel Как добавить линию тренда в диаграммуСкачать

Распознай ИНФОРМАЦИЮ | Как Определить СМЕНУ ТРЕНДА | Технический Анализ | Обучение ТрейдингуСкачать

Апроксимация набора данных в Excel инструментом Линия трендаСкачать

Лабораторная работа Прогнозирование по уравнению трендаСкачать

Как добавить линию тренда на диаграмму в ExcelСкачать

2 Кусочно-линейная интерполяция по 5 точкам MS Excel Линия трендаСкачать

Линия тренда, достоверная величина аппроксимации, функция КОРРЕЛ, ПРЕДСКАЗСкачать