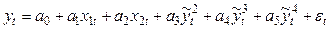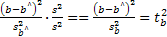Тестирование спецификации регрессионного уравнения на пропущенные переменные (5 видео)

Спецификация эконометрической модели: способы и диагностика отбора экзогенных переменных. Тесты Рамсея и Амемья.

Спецификация модели множественной линейной регрессии включает проверку:

1. правильного выбора экзогенных переменных.

2. корректного выбора формы зависимости мду эндо- и экзогенной переменными.

Для решения 1 задачи различают пропущенные и избыточные экзогенные переменные

Пропущенные переменные – существенные факторы, которые не были включены в эконометрическую модель по ошибке. Опасность наличия пропущенных переменных заключается в смещении оценок параметров при включенных переменных. Признак, по которому определяют пропущенную переменную: Знак “+” у произведения оценки параметра при подозреваемой пропущенной переменной и коэффициента корреляции этой переменной с другими переменными, включенными в модель.

Выбранная модель с пропуском переменной :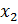

, где

Тогда, применяя МНК для оценки усеченной модели получаем формулу смещения оценки ^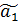

Экзогенную переменную относят к избыточным, если она по ошибке включена в эконометрическую модель. Включение избыточной переменной оказывает влияние на уменьшение точности (увеличение дисперсии) оценок параметров модели, что, в свою очередь, вызывает уменьшение t-статистик и коэффициента детерминации.

Если – избыточная, то коэффициент корреляции , тогда будет уменьшаться, а в соответствии с формулой будет возрастать.

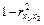
Замещающие переменные – обычно бывает полезно вместо пропущенной переменной, которую трудно измерить, использовать некоторый её заменитель.

4 основных качественных правила спецификации экономической модели:

1. Опираясь на эконометрическую теорию, следует ответить на вопрос: «Является ли переменная существенной в модели зависимости с эндогенной переменной?».

2. Осуществить проверку значимого отличия от нуля t-статистик.

3. Осуществить проверку, насколько значимо изменяется коэффициент детерминации при добавлении некоторой переменной в модель.

4. Существенно ли изменяются оценки других переменных после добавления новой переменной в модель.

Кроме отмеченных правил спецификации модели, наиболее из-вестны два следующих количественных критерия спецификации:

Критерий Рамсея (Ramsey):

RESET-тест Рамсея — это обобщенный тест на наличие следующих ошибок спецификации модели линейной регрессии:

наличие пропущенных переменных. Регрессия содержит не все объясняющие переменные;
неверная функциональная форма. Некоторые или все переменные должны быть преобразованы с помощью логарифмической, степенной, обратной или какой-либо другой функции;
корреляция между фактором Х и случайной составляющей модели, которая может быть вызвана ошибками измерения факторов, рассмотрением систем уравнений или другими причинами.

Тест Рамсея позволяет проверить, стоит ли начинать поиск дополнительной переменной для включения в уравнение

1. Оценивается уравнение регрессии

2. Вычисляются степени оценок зависимой переменной

3. Оценивается уравнение регрессии с этими степенями

4. Проводится оценка улучшения по F-критерию

Ошибки такого рода приводят к смещению среднего остатков регрессионной модели.

1. Оценивают зависимость в соответствии с выбранной моделью по МНК:

2. Анализируют вид функциональной зависимости остатков и её номинальное приближение включают в модель.

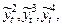
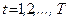
3. Например, с учетом 2) вычисляют величины , конструируют новую модель:

и применяют для ее оценивания по МНК.

4) Сравнивают качество модели по отношению к модели с помощью F-критерия:

Если где M – число дополнительных переменных, включенных в модель (M=3), k – число экзогенных переменных в то модель плохо специфицирована.

Недостаток: он указывает только на наличие ошибочной спец-ции модели, но не выявляет, сколько и какого рода переменную нужно добавить в модель.

Критерий Амемья (Amemiya):

Решающей функцией F-критерия служит:

Модель, для которой значение AF меньше, является лучше специфицированной.

Этот критерий минимизирует число экзогенных переменных.

Содержание

F-тест качества спецификации парной линейной регрессионной модели
F-тест качества спецификации множественной регрессионной модели
1. Роль степеней свободы (degree of freedom) в статистике
2. Анализ дисперсии, F-тест
3. Выбор линейной регрессионной модели
3 Проверка значимости линейной регрессии
Заключение
🎬 Видео

Видео:Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать

F-тест качества спецификации парной линейной регрессионной модели

F-тест — оценивание качества уравнения регрессии — состоит в проверке гипотезы Н₀ о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического F_выч и критического (табличного) F_крит значений F-критерия Фишера. F_выч определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы.

Коэффициент детерминации является случайной величиной (так как вычисляется по выборочным данным), и для оценки его статистической
значимости, в соответствии со стандартной процедурой, следовало бы
сравнить его вычисленное значение с табличным (критическим). Однако
таблиц распределения коэффициента детерминации не существует, поэтому для проверки статистической гипотезы о значимости R 2 используется косвенный метод: вычисляется некоторая вспомогательная статистика с известным распределением; проверяется гипотеза ее статистической значимости; устанавливается взаимосвязь между вспомогательной статисткой и коэффициентом детерминации; на основании этой взаимосвязи делается вывод о статистической значимости коэффициента детерминации. Для составления вспомогательной статистики рассмотрим две случайные величины U и V. Статистика U имеет распределение х 2 (хи-квадрат)

(1)

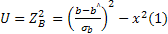
так как случайная величина 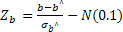, как было показано выше, имеет стандартное нормальное распределение, а ее квадрат можно рассматривать как сумму квадратов стандартных нормальных величин, включающую только одно слагаемое.

В качестве второй вспомогательной статистики, имеющей распределение х 2 с параметром, равным числу степеней свободы n — 2, используется статистика вида:

(2)

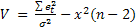
Статистика F, как легко проверить, совпадает с квадратом f-статистики для параметра b:

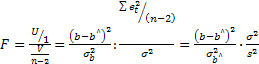
и имеет распределение Фишера с параметрами v₁=1,v₂=n-2 (n— объем выборки):

(3)

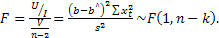
Для проверки гипотезы Н₀:b = 0 статистика (3) принимает вид:

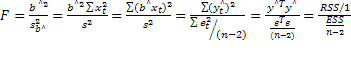
Связь между статистиками F и R 2 для случая парной регрессии
(k=2) имеет вид:

F= 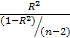(4)

Справедливость (4) проверяется непосредственно:

(5)

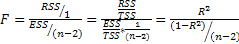
Таким образом, как следует из формулы (5), F = 0 в том случае, если R 2 =0. Поэтому, проверяя значимость F статистики (сравнивая ее вычисленное по выборочным данным значение с табличным), мы можем проверить статистическую значимость коэффициента детерминации. ЕслиF_выч

Дата добавления: 2015-01-10 ; просмотров: 5107 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Простые показатели качества модели регрессии (R2, критерии Акаике и Шварца)Скачать

F-тест качества спецификации множественной регрессионной модели

Цель этой статьи — рассказать о роли степеней свободы в статистическом анализе, вывести формулу F-теста для отбора модели при множественной регрессии.

Видео:Интерпретация коэффициента при логарифмировании в уравнениях регрессииСкачать

1. Роль степеней свободы (degree of freedom) в статистике

Имея выборочную совокупность, мы можем лишь оценивать числовые характеристики совокупности, параметры выбранной модели. Так не имеет смысла говорить о среднеквадратическом отклонении при наличии лишь одного наблюдения. Представим линейную регрессионную модель в виде:

Сколько нужно наблюдений, чтобы построить линейную регрессионную модель? В случае двух наблюдений можем получить идеальную модель (рис.1), однако есть в этом недостаток. Причина в том, что сумма квадратов ошибки (MSE) равна нулю и не можем оценить оценить неопределенность коэффициентов . Например не можем построить доверительный интервал для коэффициента наклона по формуле:

А значит не можем сказать ничего о целесообразности использования коэффициента в данной регрессионной модели. Необходимо по крайней мере 3 точки. А что же, если все три точки могут поместиться на одну линию? Такое может быть. Но при большом количестве наблюдений маловероятна идеальная линейная зависимость между зависимой и независимыми переменными (рис. 1).

Рисунок 1 — простая линейная регрессия

Количество степеней свободы — количество значений, используемых при расчете статистической характеристики, которые могут свободно изменяться. С помощью количества степеней свободы оцениваются коэффициенты модели и стандартные ошибки. Так, если имеется n наблюдений и нужно вычислить дисперсию выборки, то имеем n-1 степеней свободы.

Мы не знаем среднее генеральной совокупности, поэтому оцениваем его средним значением по выборке. Это стоит нам одну степень свободы.

Представим теперь что имеется 4 выборочных совокупностей (рис.3).

Рисунок 3

Каждая выборочная совокупность имеет свое среднее значение, определяемое по формуле . И каждое выборочное среднее может быть оценено . Для оценки мы используем 2 параметра , а значит теряем 2 степени свободы (нужно знать 2 точки). То есть количество степеней свобод Заметим, что при 2 наблюдениях получаем 0 степеней свободы, а значит не можем оценить коэффициенты модели и стандартные ошибки.

Таким образом сумма квадратов ошибок имеет (SSE, SSE — standard error of estimate) вид:

Стоит упомянуть, что в знаменателе стоит n-2, а не n-1 в связи с тем, что среднее значение оценивается по формуле . Квадратные корень формулы (4) — ошибка стандартного отклонения.

В общем случае количество степеней свободы для линейной регрессии рассчитывается по формуле:

где n — число наблюдений, k — число независимых переменных.

Видео:Множественная регрессияСкачать

2. Анализ дисперсии, F-тест

При выполнении основных предположений линейной регрессии имеет место формула:

где ,

В случае, если имеем модель по формуле (1), то из предыдущего раздела знаем, что количество степеней свободы у SSTO равно n-1. Количество степеней свободы у SSE равно n-2. Таким образом количество степеней свободы у SSR равно 1. Только в таком случае получаем равенство .

Масштабируем SSE и SSR с учетом их степеней свободы:

Получены хи-квадрат распределения. F-статистика вычисляется по формуле:

Формула (9) используется при проверке нулевой гипотезы при альтернативной гипотезе в случае линейной регрессионной модели вида (1).

Видео:Эконометрика. Линейная парная регрессияСкачать

3. Выбор линейной регрессионной модели

Известно, что с увеличением количества предикторов (независимых переменных в регрессионной модели) исправленный коэффициент детерминации увеличивается. Однако с ростом количества используемых предикторов растет стоимость модели (под стоимостью подразумевается количество данных которые нужно собрать). Однако возникает вопрос: “Какие предикторы разумно использовать в регрессионной модели?”. Критерий Фишера или по-другому F-тест позволяет ответить на данный вопрос.

Определим “полную” модель: (10)

Определим “укороченную” модель: (11)

Вычисляем сумму квадратов ошибок для каждой модели:

(12)

(13)

Определяем количество степеней свобод

(14)

Нулевая гипотеза — “укороченная” модель мало отличается от “полной (удлиненной) модели”. Поэтому выбираем “укороченную” модель. Альтернативная гипотеза — “полная (удлиненная)” модель объясняет значимо большую долю дисперсии в данных по сравнению с “укороченной” моделью.

Коэффициент детерминации из формулы (6):

Из формулы (15) выразим SSE(F):

SSTO одинаково как для “укороченной”, так и для “длинной” модели. Тогда (14) примет вид:

Поделим числитель и знаменатель (14a) на SSTO, после чего прибавим и вычтем единицу в числителе.

Используя формулу (15) в конечном счете получим F-статистику, выраженную через коэффициенты детерминации.

Видео:Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать

3 Проверка значимости линейной регрессии

Данный тест очень важен в регрессионном анализе и по существу является частным случаем проверки ограничений. Рассмотрим ситуацию. У линейной регрессионной модели всего k параметров (Сейчас среди этих k параметров также учитываем ).Рассмотрим нулевую гипотеза — об одновременном равенстве нулю всех коэффициентов при предикторах регрессионной модели (то есть всего ограничений k-1). Тогда “короткая модель” имеет вид . Следовательно. Используя формулу (14.в), получим

Видео:Регрессионное и smoke тестированиеСкачать

Заключение

Показан смысл числа степеней свободы в статистическом анализе. Выведена формула F-теста в простом случае(9). Представлены шаги выбора лучшей модели. Выведена формула F-критерия Фишера и его запись через коэффициенты детерминации.

Можно посчитать F-статистику самому, а можно передать две обученные модели функции aov, реализующей ANOVA в RStudio. Для автоматического отбора лучшего набора предикторов удобна функция step.

Надеюсь вам было интересно, спасибо за внимание.

При выводе формул очень помогли некоторые главы из курса по статистике STAT 501