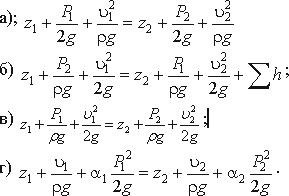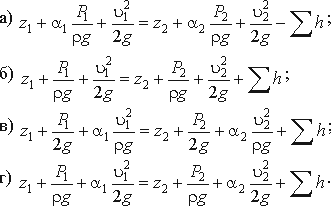Тест на тему уравнение бернулли

Видео:Закон БернуллиСкачать

Тест на тему уравнение бернулли

3.1. Площадь поперечного сечения потока, перпендикулярная направлению движения называется

а) открытым сечением;
б) живым сечением;
в) полным сечением;
г) площадь расхода.

3.2. Часть периметра живого сечения, ограниченная твердыми стенками называется

а) мокрый периметр;
б) периметр контакта;
в) смоченный периметр;
г) гидравлический периметр.

3.3. Объем жидкости, протекающий за единицу времени через живое сечение называется

а) расход потока;
б) объемный поток;
в) скорость потока;
г) скорость расхода.

3.4. Отношение расхода жидкости к площади живого сечения называется

а) средний расход потока жидкости;
б) средняя скорость потока;
в) максимальная скорость потока;
г) минимальный расход потока.

3.5. Отношение живого сечения к смоченному периметру называется

а) гидравлическая скорость потока;
б) гидродинамический расход потока;
в) расход потока;
г) гидравлический радиус потока.

3.6. Если при движении жидкости в данной точке русла давление и скорость не изменяются, то такое движение называется

а) установившемся;
б) неустановившемся;
в) турбулентным установившимся;
г) ламинарным неустановившемся.

3.7. Движение, при котором скорость и давление изменяются не только от координат пространства, но и от времени называется

а) ламинарным;
б) стационарным;
в) неустановившимся;
г) турбулентным.

3.8. Расход потока обозначается латинской буквой

3.9. Средняя скорость потока обозначается буквой

3.10. Живое сечение обозначается буквой

3.11. При неустановившемся движении, кривая, в каждой точке которой вектора скорости в данный момент времени направлены по касательной называется

а) траектория тока;
б) трубка тока;
в) струйка тока;
г) линия тока.

3.12. Трубчатая поверхность, образуемая линиями тока с бесконечно малым поперечным сечением называется

а) трубка тока;
б) трубка потока;
в) линия тока;
г) элементарная струйка.

3.13. Элементарная струйка — это

а) трубка потока, окруженная линиями тока;
б) часть потока, заключенная внутри трубки тока;
в) объем потока, движущийся вдоль линии тока;
г) неразрывный поток с произвольной траекторией.

3.14. Течение жидкости со свободной поверхностью называется

а) установившееся;
б) напорное;
в) безнапорное;
г) свободное.

3.15. Течение жидкости без свободной поверхности в трубопроводах с повышенным или пониженным давлением называется

а) безнапорное;
б) напорное;
в) неустановившееся;
г) несвободное (закрытое).

3.16. Уравнение неразрывности течений имеет вид

3.17. Уравнение Бернулли для идеальной жидкости имеет вид

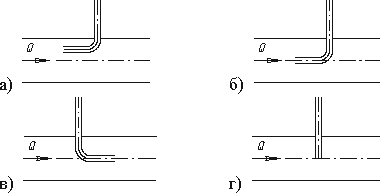
3.18. На каком рисунке трубка Пито установлена правильно

3.19. Уравнение Бернулли для реальной жидкости имеет вид

3.20. Член уравнения Бернулли, обозначаемый буквой z, называется

а) геометрической высотой;
б) пьезометрической высотой;
в) скоростной высотой;
г) потерянной высотой.

3.21. Член уравнения Бернулли, обозначаемый выражением 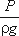называется

а) скоростной высотой;
б) геометрической высотой;
в) пьезометрической высотой;
г) потерянной высотой.

3.22. Член уравнения Бернулли, обозначаемый выражением 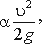называется

а) пьезометрической высотой;
б) скоростной высотой;
в) геометрической высотой;
г) такого члена не существует.

3.23. Уравнение Бернулли для двух различных сечений потока дает взаимосвязь между

а) давлением, расходом и скоростью;
б) скоростью, давлением и коэффициентом Кориолиса;
в) давлением, скоростью и геометрической высотой;
г) геометрической высотой, скоростью, расходом.

3.24. Коэффициент Кориолиса в уравнении Бернулли характеризует

а) режим течения жидкости;
б) степень гидравлического сопротивления трубопровода;
в) изменение скоростного напора;
г) степень уменьшения уровня полной энергии.

3.25. Показание уровня жидкости в трубке Пито отражает

а) разность между уровнем полной и пьезометрической энергией;
б) изменение пьезометрической энергии;
в) скоростную энергию;
г) уровень полной энергии.

3.26. Потерянная высота характеризует

а) степень изменения давления;
б) степень сопротивления трубопровода;
в) направление течения жидкости в трубопроводе;
г) степень изменения скорости жидкости.

3.27. Линейные потери вызваны

а) силой трения между слоями жидкости;
б) местными сопротивлениями;
в) длиной трубопровода;
г) вязкостью жидкости.

3.28. Местные потери энергии вызваны

а) наличием линейных сопротивлений;
б) наличием местных сопротивлений;
в) массой движущейся жидкости;
г) инерцией движущейся жидкоcти.

3.29. На участке трубопровода между двумя его сечениями, для которых записано уравнение Бернулли можно установить следующие гидроэлементы

а) фильтр, отвод, гидромотор, диффузор;
б) кран, конфузор, дроссель, насос;
в) фильтр, кран, диффузор, колено;
г) гидроцилиндр, дроссель, клапан, сопло.

3.30. Укажите правильную запись

3.31. Для измерения скорости потока используется

а) трубка Пито;
б) пьезометр;
в) вискозиметр;
г) трубка Вентури.

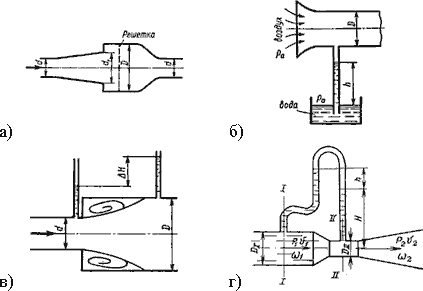
3.32. Для измерения расхода жидкости используется

а) трубка Пито;
б) расходомер Пито;
в) расходомер Вентури;
г) пьезометр.

3.33. Укажите, на каком рисунке изображен расходомер Вентури

3.34. Установившееся движение характеризуется уравнениями

3.35. Расход потока измеряется в следующих единицах

3.36. Для двух сечений трубопровода известны величины P₁, υ₁, z₁ и z₂. Можно ли определить давление P₂ и скорость потока υ₂?

а) можно;
б) можно, если известны диаметры d₁ и d₂;
в) можно, если известен диаметр трубопровода d₁;
г) нельзя.

3.37. Неустановившееся движение жидкости характеризуется уравнением

3.38. Значение коэффициента Кориолиса для ламинарного режима движения жидкости равно

3.39. Значение коэффициента Кориолиса для турбулентного режима движения жидкости равно

3.40. По мере движения жидкости от одного сечения к другому потерянный напор

а) увеличивается;
б) уменьшается;
в) остается постоянным;
г) увеличивается при наличии местных сопротивлений.

3.41. Уровень жидкости в трубке Пито поднялся на высоту H = 15 см. Чему равна скорость жидкости в трубопроводе

Видео:Урок 133. Закон Бернулли. Уравнение БернуллиСкачать

Самостоятельная работа по физике Движение жидкости. Уравнение Бернулли 10 класс

Самостоятельная работа по физике Движение жидкости. Уравнение Бернулли 10 класс с ответами. Самостоятельная работа включает 5 вариантов, в каждом по 2 задания.

Видео:Галилео. Эксперимент. Закон БернуллиСкачать

Вариант 1

1. По горизонтальной трубе переменного сечения течёт жидкость. Скорость течения в широкой части трубы 2 м/с. Определите ско­рость течения в узкой части трубы, если площади поперечного сечения этих частей трубы различаются в 1,5 раза.

2. В цилиндрическом сосуде уровень воды составляет 20 см. С ка­кой скоростью начнёт вытекать вода, если открыть кран, уста­новленный у основания этого сосуда?

Видео:Закон БернуллиСкачать

Вариант 2

1. По горизонтальной трубе переменного сечения течёт вода. Ско­рость течения в широкой части трубы 5 м/с, в узкой — 20 м/с. Во сколько раз различаются диаметры сечений этой трубы?

2. Скорость истечения воды из бассейна по трубе, расположенной в ос­новании бассейна, составляет 10 м/с. Определите глубину бассейна.

Видео:Уравнение БернуллиСкачать

Вариант 3

1. На вертикальную стену, действуя перпендикулярно, ветер оказы­вает давление 100 Па. Определите скорость ветра, если плотность воздуха равна 1,29 кг/м 3 .

2. Подводная лодка находится на глубине 100 м. С какой скоростью будет поступать вода в лодку, если открыть люк? Давление воз­духа в лодке считайте равным атмосферному.

Видео:Уравнение Бернулли гидравликаСкачать

Вариант 4

1. Из брандспойта вертикально вверх бьёт струя воды с расходом 1 кг за 1 с. Площадь поперечного сечения у основания струи равна 1,5 см 2 . Определите площадь поперечного сечения струи на высоте 2 м.

2. В горизонтальной трубе перемен­ного сечения течёт вода. Площадь поперечного сечения широкой ча­сти трубы равна 20 см 2 , узкой — 10 см 2 . Разность уровней воды в вертикальных трубках одинаково­го сечения равна 20 см (см. рису­нок).

Определите объём воды, протекающей через поперечное сечение за 1 с.

Видео:10. Уравнения БернуллиСкачать

Вариант 5

1. Для смазки инструмента используется шприц с площадью порш­ня 1 см 2 . С какой скоростью вытекает масло (ρ_м = 800 кг/м 3 ) из отверстия площадью 0,6 см 2 , если на поршень действует сила 4 Н?

2. Определите высоту, на которую поднимется вода в вертикальной трубке, впаянной в узкую часть (диаметром 3 см) горизонтальной
трубы (см. рисунок), если в широ­кой части этой же трубы (диаме­тром в 3 раза большим) скорость протекания воздуха составляет 0,25 м/с.

Ответы на самостоятельную работа по физике Движение жидкости. Уравнение Бернулли 10 класс
Вариант 1
1. 3 м/с
2. 2 м/с
Вариант 2
1. В 2 раза
2. 5 м
Вариант 3
1. ≈ 6,23 м/с
2. ≈ 44,72 м/с
Вариант 4
1. 4,8 см 2
2. ≈ 2,3 л
Вариант 5
1. 12,5 м/с
2. 0,255 м

Видео:Закон БернуллиСкачать

Тест №5 «Формула Бернулли»

Проводят n независимых опытов, в каждом из которых событие A может наступить с одинаковой вероятностью р=р(А). Вероятность неудачи в каждом опыте q=1-p.

Формула Бернулли дает вероятность того, что в n опытах событие A наступит ровно m раз:

Из этой формулы можно получить, что в n опытах наиболее вероятное число успехов будет:

Если число (np — q) целое, то m0 имеет два значения:

Если благоприятное событие соответствует нескольким значениям m, то вероятность такого успеха:

1. Станок-автомат даёт в среднем 4% брака. Взяли на проверку 30 деталей.

а) Среди них 2шт. — брак. Вероятность этого составляет.
1) 2/30 2) 0,24 3) 0,,1

б) Среди них 1 шт. — брак. Вероятность этого составляет.
1) 0,2 2) 0,/30 4) 0,04

в) Наивероятнейшее число бракованных деталей в 30шт составляет.
1 4

2. Денежный приемник автомата может сработать неправильно с вероятностью 0,03. Опустили 150 монет. Наиболее вероятное число правильной работы автомата составляет.

3. Коробку канцелярских кнопок (100шт) рассыпали по полу. Вероятность, что кнопка легла остриём вверх составляет 0,36. Следует ожидать, что на полу остриём вверх лежит … кнопок.

4. Играют два шахматиста одинаковой спортивной квалификации, т. е вероятность выиграть или проиграть одинакова. Для каждого из них вероятнее выиграть 2 партии из 4-х или 3 партии из 6-ти (без ничьих).

1) две из 4-х 2) три из 6-ти

5. Монету бросают 25 раз. Наиболее вероятно, что герб выпадет.

1) 11 и 12 рази 13 разили 14 раз

6. Монету бросают 8 раз. Вероятность того, что герб выпадет 5 раз
составляет.

1) 0,22 2) 0,44 3) 0,5

7. В семье 5 детей. Считая, что вероятность мальчика и девочки одинакова, вероятность того, что среди детей 2 мальчика составляет.

8. Игральную кость бросили 46 раз. Наиболее вероятно, что 6 очков выпадет … раз.

1) m0=6 2) m0=7 3) m0=8

9. Монету бросают 10 раз. Вероятность того, что герб выпадет от 4-х до 6-ти раз составляет.

1) 0,66 2) 0,5 3) 0,25

10. Вероятность попадания в мишень при любом одном выстреле равна
0,8. Делают 5 выстрелов в мишень.

а) Вероятность того, что будет ровно 2 попадания в мишень
составляет.

1) 0,31 2) 0,25 3) 0,0512

б) Наиболее вероятное число попаданий в мишень составляет.
1

в) Вероятность, соответствующая наиболее вероятному числу попаданий, составляет…

11. Игральную кость бросили 120 раз. Ожидают событие — «число
очков кратно 3-м». Это событие вероятнее всего наступит. раз.

12. В ящике 20 белых и 10 черных шаров. Вынимают подряд 4 шара, причем каждый раз вынутый шар возвращают в ящик перед извлечением следующего и шары перемешивают. Вероятность того, что из 4-х вынутых шаров окажутся 2 белых составляет…

1) 8/27 2) 1/4 3) 1/3

13. Вероятность того, что станок в течение часа потребует внимания рабочего, равна 0,6. Рабочий обслуживает 4 одинаковых станка. Вероятность того, что в течение часа какой-либо один станок из 4-х потребует внимания рабочего, составляет…

1) 0,1 3) 0,4

14. Для нормальной работы автобазы на линии должно быть не меньше 9-ти автомобилей, а их на автобазе 10шт. Вероятность выхода каждой автомашины на линию равна 0,9. Вероятность нормальной работы автобазы в ближайший день равна…

15. У n испытаний Бернулли число возможных элементарных событий составляет…

1) 2) 3) 2n

16. Проводят три испытания Бернулли – три раза бросают монету. Тогда вероятность любого элементарного события(ОРО, ООР и т. д.) составляет…

17. В испытании Бернулли вероятность успеха равна 0,2; тогда вероятность неудачи составляет…

1) 0,8 2) 3) 1/0,2

18. Проводят несколько испытаний в одинаковых условиях. В каждом испытании вероятность появления события А составляет 0,4. Вероятность того, что событие А произойдет 2 раза в 2-х испытаниях, составляет…

1) 0,8 2) 0,16 3) 0,24

19. Проводят несколько испытаний в одинаковых условиях. В каждом испытании вероятность появления события А составляет 0,4. Вероятность того, что событие А произойдет 2 раза в 3-х испытаниях, составляет…

20. Канцелярскую кнопку бросают на стол 400 раз. Наиболее вероятное число «успехов» — острие вверх равно 90.вероятность события: «кнопка упала острием вверх» составляет…

21. В тесте 16 задач; каждая задача имеет 4 варианта ответа, — один из них правильный. Ученик отвечает наугад. Наиболее вероятное число правильных ответов, составляет…

22. Бросают одновременно 5 игральных кубиков. Вероятность того, что на двух из пяти кубиков появится число 1, составляет…

23. Вероятность попадания при одном выстреле равна 0,2. Ожидаемое (необходимое) число попаданий равно 5. Для этого нужно произвести … выстрелов.

24. По цели стреляют 5 раз. Вероятность попадания при каждом выстреле равна 0,2. Для поражения цели достаточно не менее трех попаданий. Вероятность поражения цели составляет…

25. Монету бросают 10 раз. Вероятность того, что герб выпадет от 4-х до 6-ти раз, составляет…

1) 21/32 2) 0,5 3) 0,4

Опыт — проверка каждой из 30 деталей. Событие A — появление брака; вероятность этого ; тогда.

По формуле Бернулли:

а)

б)

в) Наивероятнейшее число брака в 30-ти деталях составляет:

По условию: n=150; p=0,97; q=0,03. По формуле: имеем:

Наивероятнейшее число вычислим так:

По условию p=q=1/2 и безразлично в какой последовательности будут выиграны партии. Значит:

Две из 4-х выиграть вероятнее, чем три из 6-ти.

n=25; p=q=0,5; по формуле:

Если в неравенстве справа и слева два целых числа, то ответ — оба этих числа.

Используем формулу Бернулли:

По условию: n=46; p=1/6; q=5/6

n=10; p=q=1/2. Вероятность:

По условию n=5; p=0,8; q=0,2.

а) вероятность ровно 2-х попаданий:

б) Наиболее вероятное число попаданий:

в) Вероятность соответствующая m0 = 4 будет:

По формуле: , получим

Вероятность извлечения белого шара одинакова во всех 4-х случаях.

По формуле Бернулли:

По формуле Бернулли:

(1)=∙∙=4∙0,6∙=0,1536

(9, 10)=(9) +(10)=∙∙0,1+ ∙=

У n испытаний Бернулли число возможных событий равно

Вероятность любого элементарного события в испытании Бернулли равна 1/=1/=1/8

В испытании Бернулли q=1 — p=1 — 0,2=0,8

(2)=∙∙=1∙∙1=0,16

(2)=∙∙=3∙∙0,6=0,288

=n∙p → 90=400∙p → p=90/400=0,225

n=16; p=1/4; =n∙p=16∙1/4=4

(2)=∙∙=10∙ 125/7776≈0,161

=5; p=0,2 → =n∙p

По условию: n=5; р=0,2; q=0,8

Цель будет поражена, если в нее попадут 3,4 или 5 раз из пяти выстрелов, т. е.

p= (3)+(4)+(5)

(3)=∙∙=0,0512

(4)=∙∙=0,0064

(5)=∙=0,00032

p(4≤k≤6) =(4)+(5)+(6)

(4)=∙∙=∙=210/1024

(5)=∙∙=∙=252/1024

(6)=∙∙=∙=210/1024

💥 Видео

Дифференциальные уравнения, 5 урок, Уравнение БернуллиСкачать

Уравнение Бернулли Метод БернуллиСкачать

Уравнение Бернулли. Практическая часть. 10 класс.Скачать

Уравнение Бернулли. Диаграмма Бернулли.Скачать

Уравнение Бернулли для потока жидкостиСкачать

🌑 Интересный эксперимент не показывать детям! Физика в ванной Закон Бернулли #Shorts Игорь БелецкийСкачать

Уравнение БернуллиСкачать

Уравнение Бернулли и его приложения | Гидродинамика, ГидравликаСкачать

Урок 134. Применения уравнения Бернулли (ч.1)Скачать

Лайфхак закон БернуллиСкачать

Закон Бернулли и движение по инерцииСкачать

ЛР3 Уравнение БернуллиСкачать