Главная страница — на ней вы найдете информацию по стоимости и примеры работ.
Примеры вопросов по предмету
Здесь Вы найдете некоторые из тестовых вопросов, на которые мы можем помочь Вам ответить.
Ответы на некоторые вопросы теста
Здесь Вы найдете ответы на несколько вопросов по данному предмету
Для заявки
Здесь Вы сможете оставить заявку и посмотреть контакты для связи.
Видео:Математика это не ИсламСкачать

Математика и Математический анализ
Сдача (решение) одного теста по данному предмету — 100 руб.
Список некоторых вопросов из тестов, на которые мы можем помочь с ответами.
• Непрерывная двумерная случайная величина распределена внутри прямоугольного треугольника с вершинами О (0;0), А(0;14), В(14;0). Найти плотность системы.
• Найти угол между векторами a и b a = и b =
• Найдите значение х, при котором векторы a(3;2х;–1), b(2;5;–2). a и b будут ПЕРПЕНДИКУЛЯРНЫ
• Найдите значение х, при котором векторы a(3;2;–1), b(2;х;–2). a и b будут ПАРАЛЛЕЛЬНЫ
• Найдите координаты середины отрезка A = (9;5) В=(7;10)
• Задано распределение двумерной случайной величины. Найти распределения X и Y 0.24
• Задано распределение двумерной случайной величины. Найти безусловные математические ожидания и дисперсии. X и Y
• Найти корреляционный момент случайных величин X и Y, заданных распределением:12-30.15
• Найти коэффициент корреляции случайных величин X и Y, заданных распределением: 0.17 0.1
• Возведите число x = 2 в степень p = frac 32
• Переведите координаты точки A (4; 1) из декартовой системы координат в полярную:
• Место точки в пространстве координат определяется …
• Из точек А(-2;2), C(2;0), С(9;-5), Р(0;-8) выберите те, которые лежат на оси абсцисс:
• Найти предел последовательности lim_frac =?
• Какими преобразованиями можно получить график функции y = sqrt из графика функции y = sqrt x?
• Заданы точки: А (-2;1), В(-2; 6), С(2;-5), К(-2;-7). Какой из отрезков параллелен оси ординат?
• Запишите с помощью знака модуля неравенство -3 0 степенная функция определена в точке
• При целых значениях p степенная функция определена в области
• График функции y = x^p, где p>1, выглядит следующим образом:
• Выберите верный график функции y=ln 2x:
• Логарифмическая функция убывает при…
• При возведении в степень показатели степеней
• Исследуйте функцию y=sqrt x на четность
• Какими преобразованиями получается график функции y= f(-x) из графика функции y=f(x)?
• При любом действительном значении показатели степени p степенная функция определена в области
• Пределом последовательности Ɛ называется …
• Возвести число x в дробную степень p=frac mn значит…
• Пределом функции y=f(x) в точке x_0 называется …
• Отметьте сходящиеся ряды n+5
• Найдите сумму ряда 5/7
• Найдите сумму ряда 2/7
• Отметьте условно сходящиеся ряды
• Найдите сумму ряда 5/8
• Отметьте абсолютно сходящиеся ряды (n+3)3
• Расстояние |ab| между точками a=M(xa, ya) и b=M(xb, yb) определяется по формуле:
• Расстояние |ab| между точками a=M(x_a, y_a) и b=M(x_b, y_b) определяется по формуле:
• Оси координат разбивают плоскость на четыре части, которые называются …
• Проекции (x_a, y_a) заданной точки на две взаимно перпендикулярные числовые оси Ox и Oy это …
• Если принять начало координат за полюс, а ось Ox за полярную ось, взаимная связь декартовых координат и полярных координат точки может быть выражена следующими формулами:
• Число C = (A) называется максимумом (наибольшим элементом) некоторого подмножества действительных чисел A, если …
• Полюс это …
• Логарифмическая функция возрастает при…
• Логарифмическая функция не существует при…
• Период функции y = ctgx:
• Показательная функция возрастает при…
• Переведите комплексное число z = 4(cospi + icdotsinpi) из тригонометрической формы в алгебраическую:
• Переведите комплексное число из тригонометрической формы в алгебраическую:
• Величинаsin22x равна:
• Число a называется пределом функции y=f(x) при x стремящемся к бесконечности, если …
• Числовая последовательность это …
• Найти предел функции lim_frac =?
• Какая из перечисленных функций является непрерывной на всей числовой прямой?
• Из точек А(-2;0), В(2;0), С(9;-5), Р(0;-8) выберите те, которые лежат на оси абсцисс:
• Абсцисса и ордината заданной точки называются … точки.
• Второй замечательный предел:
• Выберите верное определение понятия график
• Чему равна сумма ряда sum^5_2+2^?
• График какой функции получится, если y = x^3 перенести на 5 единицы влево вдоль оси OX?
• При любом действительном значении показателя степени p функция y = x^p определена в области
• Переведите комплексное число z = 6(cosfrac6 + icdotsinfrac6)из тригонометрической формы в алгебраическую:
• Найдите общий интеграл дифференциального уравнения dy/y=x21dx
• Дано дифференциальное уравнение xy’=y-5 при y(5)=5. Выберите интегральную кривую, которая определяет его решение
• Найдите общий интеграл дифференциального уравнения dy/y6=x7dx
• Дано дифференциальное уравнение xy’=y-10 при y(10)=10. Выберите интегральную кривую, которая определяет его решение
• Дано дифференциальное уравнение y’=4x при y(0)=2. Выберите интегральную кривую, которая определяет его решение
• Найдите решение дифференциального уравнения y’=-6y+2
• Установите соответствие между дифференциальным уравнением и его типом
• Найдите решение дифференциального уравнения y’=-7y+3
• Укажите правильное решение линейного однородного дифференциального уравнения второго порядка с постоянным коэффициентами y»+4y’-3y=0
• Определите вид частного решение для неоднородного дифференциального уравнения y»-2y=x+4
• Найдите общий интеграл дифференциального уравнения dy/y4=x7dx
• Укажите правильное решение линейного однородного дифференциального уравнения второго порядка с постоянным коэффициентами y»-y’-2y=0
• Производная функции S(t)=-5e5t+3ln6t
• Установите соответствие между дифференциальным уравнением и его типом
• Найдите общий интеграл дифференциального уравнения dy/y=x6dx
• Дано дифференциальное уравнение y’=-x при y(0)=2. Выберите интегральную кривую, которая определяет его решение
• Установите соответствие между дифференциальным уравнением и его типом
• Установите соответствие между дифференциальным уравнением и его типом
• Дано дифференциальное уравнение xy’=y-26 при y(27)=26. Выберите интегральную кривую, которая определяет его решение
• Найдите решение дифференциального уравнения y’=-2y+3
• Определите вид частного решение для неоднородного дифференциального уравнения y»-2y’=5e2x
• Установите соответствие между дифференциальным уравнением и его типом
• Определите вид частного решение для неоднородного дифференциального уравнения y»-5y’=x+1
• В вазе 5 апельсинов, 6 бананов и 7 яблок. Найдите вероятность того, что вынутый фрукт не апельсин
• В вазе 10 яблок, 12 бананов и 8 апельсинов. Найдите вероятность того, что вынутый фрукт не яблоко
• В вазе 13 бананов, 10 яблок и 7 апельсинов. Найдите вероятность того, что вынутый фрукт не банан
• Случайная величина ξ нормально распределена с параметрами a=-10, b=10. С точностью 2 знака после запятой найдите P(ξ
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

ТЕСТЫ ПО ДИСЦИПЛИНЕ «МАТЕМАТИЧЕСКИЙ АНАЛИЗ»
Тесты для проверки усвоения пройденного материала
по дисциплине «Математический анализ»
для студентов заочного отделения
Просмотр содержимого документа
«ТЕСТЫ ПО ДИСЦИПЛИНЕ «МАТЕМАТИЧЕСКИЙ АНАЛИЗ»»
Тесты для проверки усвоения пройденного материала
по дисциплине «Мтематический анализ»
ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
Последовательность 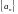
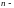
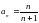
а) возрастающей; б) убывающей; в) неограниченной; г) невозрастающей.
Последовательность 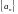
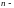
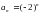
а) возрастающей; б) неубывающей; в) неограниченной; г) ограниченной.
Предел последовательности 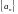
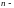
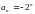
а) 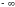

Предел последовательности 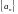
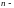

а) 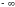

Предел последовательности 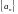
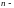
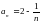
а) 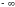

Предел последовательности 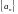
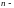
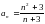
а) 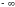

Предел последовательности 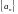
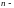
а) 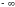

Среди перечисленных вариантов ответов выбрать значение предела :
а) 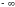
Среди перечисленных вариантов ответов выбрать значение предела :
Среди перечисленных вариантов ответов выбрать значение предела :
а) 1; б) 0; в) 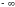

Указать числовой промежуток, на котором определена функция :
Указать числовой промежуток, на котором определена функция :
Указать числовой промежуток, на котором определена функция :
Какова область значений функции :
Какова область значений функции :
Какова область значений функции :
Какое из перечисленных свойств относится к функции :
а) функция является чётной; б) функция является нечётной; в) функция является функцией общего вида; г) функция является периодической.
Какое из перечисленных свойств относится к функции :
а) функция является чётной; б) функция является нечётной; в) функция является функцией общего вида; г) функция является периодической.
Какая из перечисленных функций является обратной для функции на промежутке :
Какая из перечисленных линий является графиком функции :
а) кубическая парабола; б) квадратичная парабола; в) гипербола; г) экспонента.
Какая из перечисленных линий является графиком функции :
а) кубическая парабола; б) квадратичная парабола; в) гипербола; г) экспонента.
Какое из перечисленных утверждений истинно? Функция на всей области определения является:
а) неубывающей; б) невозрастающей; в) неотрицательной; г) неположительной.
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения. Однородное уравнение.Скачать

Тест «Дифференциальное и интегральное исчисление»
Тест по тема 3.1. Дифференциальное и интегральное исчисление
- Производная это …
- предел произведения приращения функции и приращения аргумента при
.
- предел отношения приращения функции к приращению аргумента при
.
- предел суммы приращения функции и приращения аргумента при
.
- предел разности приращения функции и приращения аргумента при
.
2. Уравнение касательной имеет вид:
а.
b.
c.
d.
3. Если при переходе через критические точки I рода производная меняет свой знак с «+»
а. функция имеет максимум
b. функция имеет минимум
c. не имеет экстремума
d. ваш вариант ответа
- Если производная функции y = f(x) в данном промежутке …, то функция возрастает в этом промежутке
5. Приращение F(b) – F(a) любой из первообразных функций F(x)+c при изменении аргумента от 

a. 

6. Геометрический смысл производной заключается в том, что производная это …
- площадь криволинейной трапеции
- угловой коэффициент касательной
- ускорение прямолинейного движения материальной точки в любой момент времени
- мгновенная скорость прямолинейного движения материальной точки в любой момент времени
7. Точки экстремума это точки…
- в которых промежутки выпуклости меняются на промежутки вогнутости
- максимума и минимума
- в которых производная равна нулю или не существует
- ваш вариант.
9. Производная произведения двух функций равна …
a. 

10. Если при переходе через критические точки I рода производная меняет свой знак с «-»
а. функция имеет максимум
b. функция имеет минимум
c. не имеет экстремума
d. ваш вариант ответа
11. Геометрический смысл определенного интеграла заключается в том, что определенный интеграл это …
- площадь криволинейной трапеции
- угловой коэффициент касательной
- ускорение прямолинейного движения материальной точки в любой момент времени
- мгновенная скорость прямолинейного движения материальной точки в любой момент времени
12. Механический смысл первой производной заключается в том, что производная это …
- площадь криволинейной трапеции
- угловой коэффициент касательной
- ускорение прямолинейного движения материальной точки в любой момент времени
- мгновенная скорость прямолинейного движения материальной точки в любой момент времени
13. Если вторая производная функции y = f(x) в данном промежутке значений х положительна, то кривая в этом промежутке …
15. Функция F(x) называется первообразной для всех f(x), если выполняется равенство:
a.
b.
c.
d. Ваш вариант ответа
- Производная частного двух функций равна …
- Точки перегиба это точки…
- в которых промежутки выпуклости меняются на промежутки вогнутости
- максимума и минимума
- в которых производная равна нулю или не существует
- ваш вариант.
- Критические точки это точки…
- в которых промежутки выпуклости меняются на промежутки вогнутости
- максимума и минимума
- в которых производная равна нулю или не существует
- ваш вариант.
- Формула Ньютона-Лейбница:
- Множество всех первообразных для функции y = f(x) имеет вид:
а. 


📹 Видео
2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать

Математика без Ху!ни. Ряды. Часть 1. Сумма ряда. Сходимость. Геометрическая прогрессия.Скачать

13. Как решить дифференциальное уравнение первого порядка?Скачать

Математика без ху!ни. Интегралы, часть 1. Первообразная. Дифференцирование и интегрирование.Скачать

Проверка интеграла Проверить дифференцированием интегралСкачать

6. Числовые ряды. Интегральный признак КошиСкачать

Дельта альфа альфа штрих | МФТИСкачать

Дифференциальные уравнения. 11 класс.Скачать

Приближенное вычисление интеграла с помощью ряда Тейлора. 2-ой пример.Скачать

КАК РАЗОБРАТЬСЯ В ВЫСШЕЙ МАТЕМАТИКЕСкачать

Применение степенных рядов к решению дифференциальных уравнений.Скачать

Как распознать талантливого математикаСкачать

Математика без Ху!ни. Метод неопределенных коэффициентов.Скачать

Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать

Математика без ху!ни. Несобственные интегралы, часть 1. Сходимость и расходимость.Скачать


 .
. .
.













