Термодинамическая вероятность и энтропия связаны уравнением больцмана (8 видео)

Связь энтропии с термодинамической вероятностью

Термодинамической вероятностью W какого-либо состояния называют число микросостояний, с помощью которых может быть осуществлено данное макросостояние. Каждое термодинамическое состояние можно рассматривать как с макроскопической, так и с микроскопической точек зрения.

Все доступные микросостояния равновероятны за длительный период времени – эргодическая гипотеза.

Энтропия связана с термодинамической вероятностью соотношением 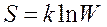, где k – постоянная Больцмана. Таким образом, энтропия – скалярная физическая величина, характеризующая макросостояние термодинамической системы, и численно равная постоянной Больцмана, умноженной на натуральный логарифм термодинамической вероятности этого состояния.

Основное неравенство термодинамики:

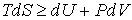Термодинамическая вероятность и энтропия связаны уравнением больцмана

(11.19)

В этом выражении знак равенства соответствует равновесным термодинамическим процессам, а знак неравенства — неравновесным.

Основное уравнение термодинамики равновесных (обратимых) процессов:

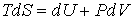(11.20)

Дата добавления: 2017-06-02 ; просмотров: 3012 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:2 Лекция 16 Формула БольцманаСкачать

Термодинамическая вероятность и энтропия.

Энтропия — это показатель неупорядоченности системы. Чем выше энтропия, тем хаотичнее движение материальных частиц, составляющих систему.

Для определения физического содержания энтропии берут отношение теплоты Q, которое получило тело в изотермическом процессе, к температуре Т теплоотдающего тела, называемое приведенным количеством теплоты.

Приведенное количество теплоты, которое сообщается телу на малом участке процесса, равно δQ/T. Строгий формальный анализ показывает, что приведенное количество теплоты, которое сообщается телу в любом обратимом круговом процессе, равно нулю:

Из равенства нулю интеграла, взятого по замкнутому контуру, следует, что подынтегральное выражение δQ/T есть полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от пути, которым система пришла в это состояние. Таким образом,

Функция состояния, у которой дифференциал равен δQ/T, называется энтропией и обозначается S.

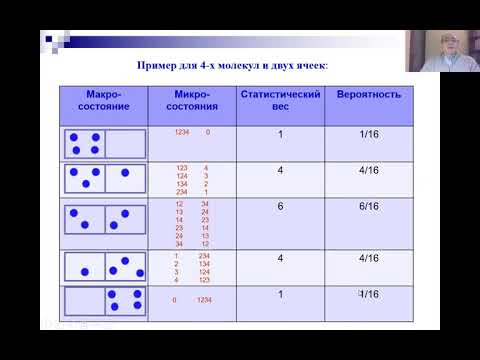
Термодинамическая вероятность W состояния системы — это число способов, с помощью которых может быть реализовано данное состояние макроскопической системы, или число микросостояний, которые осуществляют данное макросостояние.

Cогласно Больцману, энтропия cиcтемы и термодинамическая вероятность связаны между собой следующим образом:

,где k — постоянная Больцмана.

Таким образом, энтропия определяется логарифмом числа микросостояний, с помощью которых может быть осуществлено данное макросостояние. Значит, энтропия может рассматриваться как мера вероятности состояния термодинамической системы. Формула Больцмана позволяет дать энтропии следующее статистическое толкование: энтропияявляется мерой неупорядоченности системы. Действительно, чем больше число микросостояний, которые реализуют данное макросостояние, тем больше энтропия. В состоянии равновесия — наиболее вероятного состояния системы — число микросостояний максимально, при этом также максимальна и энтропия.

Второй закон термодинамики.

Второй закон термодинамики — физический принцип, накладывающий ограничение на направление процессов, которые могут происходить в термодинамических системах.

Второй закон термодинамики запрещает так называемые вечные двигатели второго рода, показывая, что коэффициент полезного действия не может равняться единице, поскольку для кругового процесса температура холодильника не может равняться абсолютному нулю.

Видео:Энтропия и вероятность. Часть 4. Формула Больцмана. Связь энтропии и термодинамической вероятности.Скачать

Начала термодинамики. Энтропия и вероятность. Принцип Больцмана

Термодинамика сначала исследовала тепловые явления, а после установления закона сохранения и превращения энергии стала изучать также превращения энергии во всех ее формах. Термодинамика основана на трех-четырех утверждениях, которые включили в себя огромный опыт человечества по превращению энергии и называются началами термодинамики. Исторически первым установлено второе начало, потом — первое и третье, а последним — нулевое.

Нулевое начало термодинамики уточняет понятие температура. Тепловое равновесие существует, если система А приведена в тепловой контакт с системой В, но потоки энергии отсутствуют. Количественно введено понятие температуры: если системы А и В имеют одинаковую температуру, то системы находятся в тепловом равновесии друг с другом.

Первое начало термодинамики — это закон сохранения и превращения энергии в изолированной системе, утверждение существования внутренней энергии, поэтому его называют принципом энергии. Энергия утвердилась как основная сохраняющаяся величина (1847), когда договорились о терминах Кельвин и Джоуль. Теплота и работа определяют способы передачи энергии.

Второе начало термодинамики устанавливает направленность всех процессов в изолированных системах. Кельвин и Кла-узиус отделили это начало — хотя полное количество энергии сохраняется в любом процессе, распределение энергии изменяется необратимо. Второе начало называют принципом энтропии. Теплота переходит самопроизвольно только от более нагретых тел к менее нагретым. При этом для направления, в котором происхо-

дит изменение распределения энергии, оказывается не важно само количество энергии. Это начало проявилось при преобразовании теплоты в полезную работу, оно сыграло важнейшую роль в преобразовании энергии, запасенной в топливе, в движущую силу. Ограничения, устанавливаемые вторым началом термодинамики, показали, что трудно выделить упорядоченное движение из неупорядоченного. В формулировке Кельвина второе начало таково: «Невозможен процесс, единственный результат которого состоял бы в поглощении теплоты от нагревателя и полного преобразования этой теплоты в работу».

Третье начало термодинамики определяет свойства веществ при очень низких температурах, утверждая, что нельзя охладить тела до температуры абсолютного нуля за конечное число процессов. Оно предполагает атомное строение вещества, тогда как остальные являются обобщением опытных данных и не содержат сведений о какой-либо структуре вещества.

Достоинство термодинамики в том, что она позволяет рассмотреть общие свойства систем при равновесии и общие закономерности установления равновесия, получить многие сведения о веществе, не зная в полной мере его внутреннюю структуру. Ее законы применимы к любому веществу, к любым системам, включающим электрические и магнитные поля и излучение, поэтому они вошли в физику газовых и конденсированных сред, химию и технику, необходимы в геофизике и физике Вселенной, используются в биологии и управлении процессами. В начале XX в. американский ученый Гиббс разработал метод термодинамических потенциалов, в котором состояние системы характеризуется той или иной функцией: внутренней энергией, энтальпией, свободной энергией или потенциалом Гиббса (см. гл. 8). Термодинамика строилась как классическая динамическая теория, так как все устанавливаемые ею связи носили однозначный характер и все описываемые ею явления объяснялись как абсолютно необходимые. Как и в механике, случайность не входит в теорию.

Энтропия — мера беспорядка в системах, как и сами понятия порядка и беспорядка, приобретает фундаментальное значение. Более глубокое толкование и понимание смысла энтропии и начал термодинамики было дано с позиций статистической физики. Если каждое макроскопическое состояние газа может быть получено с определенной вероятностью, то вероятность может быть вычислена через вероятности микросостояний.

Термодинамической вероятностью W называют число микросостояний, которыми может быть осуществлено данное макроскопическое состояние. Замена одной микрочастицы на другую из-за их неотличимости не меняет макроскопического состояния, хотя с микроскопической точки зрения ситуация изменилась. Свойства термодинамической вероятности похожи на свойства энтро-

пии — обе максимальны в состоянии равновесия, и переход к равновесию связан с их ростом. Энтропия является аддитивной (от лат. additivus — придаточный) величиной и пропорциональна логарифму термодинамической вероятности: Это извест-

ное выражение определяет принцип Больцмана.

Пусть сначала газ, содержащий N молей, занимает объем V₁ после открытия заслонки он расширился в объем V₂. При этом логарифм вероятности его возрос на величину Сравним ее с величиной изменения энтропии при расширении газа в пустоту: они отличаются только единицами измерения, и при умножении логарифма вероятности на величину R/N получим изменение энтропии при необратимом процессе. Итак, логарифм изменения вероятности состояния с точностью до постоянного множителя совпадает с изменением энтропии. Больцман считал атомистическую гипотезу обоснованной. Бесконечное или огромное число частиц делает невозможным механическое, требует статистического описания. Математическим инструментом статистики является исчисление вероятностей. Больцман показал, что поскольку в основе термодинамических процессов лежат обратимые кинетические процессы, то необратимость в термодинамике, измеряемая энтропией, не может быть абсолютной. Поэтому и энтропия должна быть связана с вероятностью осуществления данного микросостояния.

Понятие вероятности, неявно использованное Максвеллом, Больцман применил для преодоления трудностей, связанных с пониманием второго начала термодинамики и гипотезы «тепловой смерти Вселенной» (1878). Вершиной творчества Больцмана явилось установление связи между энтропией и термодинамической вероятностью. Планк записал эту связь через введение константы k = R/N, которую назвал постоянной Больцмана.

Итак, необратимый процесс есть переход из менее вероятного состояния в более вероятное, а логарифм изменения вероятности состояния с точностью до постоянного множителя совпадает с изменением энтропии состояния. Эту связь Больцман установил сначала для идеального газа.

Чем выше степень беспорядка в координатах и скоростях частиц системы, тем больше вероятность того, что система будет в состоянии хаоса. Формула Больцмана может рассматриваться как определение энтропии.

Поскольку S увеличивается с ростом W, и все системы стремятся перейти в более вероятное состояние, то и изменение энтропии S₂ — S₁ =

При расширении газа в пустоту пропорционально соответствующему изменению объемов в степени N, поэтому для изменения энтропии можно записать Nkln(V₁/V₂). Умножая и деля это выражение на Г, получим: Но так как

то в числителе формулы для изменения энтропии стоит подводимая к системе по обратимому пути теплота.

Рассмотрим два одинаковых по массе т и удельной теплоемкости с тела, которые первоначально имели разные температуры После

установления между ними теплового контакта в результате перехода теплоты dQ их температуры изменились: Поскольку dQ =

равны, то и

Если для каждого процесса можно записать:

Суммарное изменение энтропии равно: а

температуры Так как

или

Это значит, что при теплота будет самопроизвольно

перетекать от тела с более высокой температурой к менее нагретому телу. И при увеличении энтропии замкнутой системы, содержащей тела с разными температурами, ее рост сопровождается потерями механической работы в количестве, равном величине dS, умноженной на температуру более холодного тела. Можно ли уменьшить энтропию? Второе начало термодинамики применимо только к изолированным системам, при совместном рассмотрении всех частей системы энтропия не уменьшается.

Деятельность человека может приводить к локальному уменьшению энтропии. Холодильники и тепловые насосы перекачивают теплоту от холодного тела к более горячему за счет траты энергии извне, но в полной системе энтропия может только расти. Больцману удалось установить в теории газов основное различие между тепловыми и механическими явлениями, которое долгое время было главным аргументом против всякой кинетической теории. Механические явления обратимы, и знак времени в них не играет никакой роли, тогда как тепловые явления так же необратимы, как и выравнивание двух температур. Если теория газов, основанная на механике, приводит к необратимым явлениям, то это связано с гипотезой молекулярного беспорядка, и аналогия с ростом энтропии здесь очевидна. В настоящее время понятие энтропии получило дальнейшее развитие в теории информации, лежащей в основе кибернетики, но об этом речь будет идти позже.