Тепловой режим электродвигателя уравнение нагрева и охлаждения (4 видео)

Содержание

Нагрев и охлаждение электродвигателей
Нагрев и охлаждение электродвигателей
ТЕПЛОВОЙ РЕЖИМ И НОМИНАЛЬНАЯ МОЩНОСТЬ ДВИГАТЕЛЯ
📽️ Видео

Видео:Защита электродвигателя. Настройка теплового реле на электродвигателе!Скачать

Нагрев и охлаждение электродвигателей

Тепловой режим электродвигателя зависит от нагрузки и от интенсивности его охлаждения. Во время работы двигателя его температура Т_ДВ не должна быть выше предельно допустимой температуры. Большинство двигателей охлаждаются вентиляторами, которые установлены на валу со стороны задней крышки статора. Однако для правильного выбора двигателя, предназначенного для работы в любом из основных режимов, необходимо знать закон изменения во времени превышения температуры υ двигателя над температурой окружающей среды Т_СР (υ = Т_ДВ — Т_СР).

В большинстве случаев использования двигателя широко распространенных типов приводов с продолжительным режимом работы его мощность рассчитывается по эмпирическим формулам, помещенным в справочники. Для малоизученных приводов с этим режимом работы мощность двигателя определяют опытным путем либо рассчитывают на основе удельного расхода энергии при выпуске продукции.

При кратковременном и повторно-кратковременном режимах, когда не требуется высокая точность, используют упрощенный метод расчета, основанный на предположении, что двигатель представляет собой однородное тело. В этом случае процесс нагрева двигателя можно описать уравнением:

(6.2)

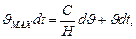
где С – теплоемкость электродвигателя; Н – теплоотдача электродвигателя; υ _MAX = Q₀/H; Q₀ – тепловая мощность (тепловая энергия, образующаяся в двигателе в единицу времени).

Решение уравнения (6.2) будет иметь вид:

(6.3)

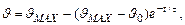
где τ = С/Н – постоянная времени нагрева электродвигателя, определяемая экспериментальным путем; υ₀ – начальное значение превышения температуры.

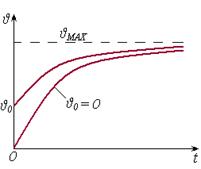Тепловой режим электродвигателя уравнение нагрева и охлаждения

Рис. 6.1 – Графическая зависимость υ(t)

Графически зависимость υ(t), полученная согласно выражению (6.3), приведена на рис. 6.1. При υ₀ = 0 эта зависимость нарастает по экспоненциальному закону, стремясь к значению υ_MAX. При υ₀ > 0 изменяется только скорость возрастания превышения температуры υ. Характер процесса остается экспоненциальным. Построение таких графиков позволяет оценивать возможности использования двигателя по его загруженности.

При повторно-кратковре-менном режиме электродвигатель попеременно то нагревается, то охлаждается. Изменение его температуры в каждом таком цикле зависит от предыдущего цикла (Рис. 6.2). Если в каком-то цикле происходит значительное изменение условий охлаждения (длительная остановка двигателя, существенное изменение температуры окружающей среды), то изменится постоянная времени нагрева электродвигателя, что приведет к изменению скорости процессов нагрева и охлаждения. Это необходимо учитывать при построении графиков нагрева.

Такие графики, хотя и отображают наглядно процессы нагрева и охлаждения двигателя, однако не дают точных результатов и требуют много времени на их построение.

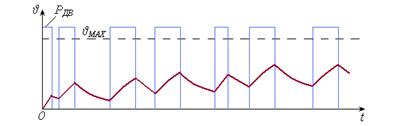Рис. 6.2 – График нагрева двигателя при повторно-кратковременном режиме работы

На практике для выбора мощности двигателя применяют более простые методы, такие как метод эквивалентного тока иметод эквивалентного момента.

В основу метода эквивалентного тока положено допущение, что при переменной нагрузке на двигатель его средние потери равны потерям при продолжительной номинальной нагрузке. Так как мощность переменных потерь пропорциональна квадрату рабочего тока I и сопротивлению соответствующей обмотки R, то суммарные потери энергии W_∑ за все рабочее время Т, равное сумме отдельных рабочих промежутков времени двигателя, должны быть равны

(6.4)

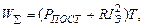
где Р_ПОСТ – мощность постоянных потерь (трение, потери в магнитопроводе, затраты на возбуждение); I_Э – эквивалентный ток.

Эквивалентный ток определяется как

(6.5)

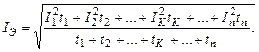
Если известен эквивалентный ток, номинальное напряжение и номинальный коэффициент мощности, то можно определить номинальную мощность двигателя:

Метод эквивалентного тока применим при постоянных потерях в двигателе в течение всего рабочего времени. Это условие, например, не выполняется в двигателях с последовательным возбуждением, у которых при изменении нагрузки изменяются магнитный поток и частота вращения, соответственно будут изменяться потери в магнитопроводе и потери на трение.

Метод эквивалентного момента базируется на том, что у всех электродвигателей вращающий момент пропорционален произведению тока и магнитного потока. Магнитный поток можно считать практически постоянным у всех двигателей, кроме двигателей с последовательным и смешанным возбуждением. В этом случае М_ВР = k_BP I (k_BP — постоянная величина). Тогда

(6.7)

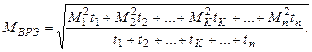
По известному моменту М_ВРЭ и номинальной угловой скорости ω_НОМ получают номинальную мощность двигателя

Видео:Количество теплоты, удельная теплоемкость вещества. 8 класс.Скачать

Нагрев и охлаждение электродвигателей

Для обеспечения нормального режима эксплуатации электрических машин необходимы знания теплового режима работы изоляции электродвигателя.

Учет всех тепловых процессов, происходящих в электрической машине, задача далеко не из легких, так как существует различие материалов, использованных при изготовлении электродвигателя (медь, изоляция, электротехническая сталь), условия работы элементов (вращающиеся и неподвижные), а также довольно сложные процессы обмена тепла между отдельными частями электродвигателя.

В процессе работы электродвигателя избежать потерь в нем невозможно. Эти потери будут вызывать нагрев отдельных компонентов и создавать процессы теплообмена. Поэтому при изучении процессов нагрева и охлаждения электрическую машину рассматривают как систему нескольких однородных тел, которые связаны взаимными тепловыми потоками.

Например, асинхронный электродвигатель следовало бы рассматривать как систему четырех тел, а именно: сталь и медь статора, которые разделены изоляцией, медь и сталь ротора, а также охлаждающая среда. При подобных допущениях тепловые процессы внутри асинхронного электродвигателя будут описываться довольно сложной системой дифференциальных уравнений. В случае же переменной нагрузки система уравнений значительно усложняется, что делает расчет практически невозможным.

Более простым случаем является нагрев двух тел. В таком случае нагревание статора и ротора рассматривается отдельно друг от друга. Нагрев каждого из этих элементов рассматривают как процессы теплообмена между медью и сталью под действием соответствующих потерь. Однако даже такое весьма упрощенное и приближенное рассмотрение процессов теплообмена электрических двигателей требует значительного количества конструктивных и расчетных параметров, таких как теплоотдача лобовых частей обмотки статора, теплоотдача между медью и сталью ротора через пазовую изоляцию и другие параметры. Эти данные в каталогах производители не приводят, что делает подобные методы расчета практически недоступными для проектировщиков систем электроприводов, не говоря уже об эксплуатирующем персонале. В случаях необходимости установления нагрева электродвигателя при определенной нагрузке используют более грубые и простые методы.

Упрощение достигается тем, что процесс нагревания электрической машины заменяют процессом нагревания однородного твердого тела, обладающего бесконечно большой теплопроводимостью. Этому телу на единицу времени по всему объему будет передано определенное количество тепла, которое определяется потерями:

Где Р – мощность полезная на валу машины; η – КПД соответствующий данной нагрузке.

При нагревании электромашины ее температура повышается. Как только она превысит температуру окружающей среды — электродвигатель станет излучать тепло и, соответственно, процесс нагрева замедлится. С увеличением температуры электродвигателя будет увеличиваться и количество теплоты, отдаваемое им в окружающую среду. При определенной температура наступает тепловое равновесия – это когда количество теплоты, получаемое объектом, равно количеству теплоты отдаваемой им. При достижении равновесия температура установится на определенном уровне и не будет изменятся.

Отдача тепла телом может происходить тремя способами – конвекцией, лучеиспусканием, теплопроводностью.

Тепло, отдаваемое лучеиспусканием, будет пропорционально разности четвертых степеней абсолютных температур тела и среды.

Тепло, отдаваемое при конвекции, пропорционально разности температур в степени 1,25; а в случае с теплопроводностью – пропорционально данной разности.

Ввиду того, что температуры нагрева в электромашиностроении не велики, количество тепла, отдаваемое путем лучеиспускания, будет весьма невелико и им, как правило, пренебрегают. Наиболее существенное влияние оказывают процессы конвекции и теплопроводимости, поэтому для упрощения расчетов в дальнейшем принимается, что отдаваемое тепло пропорционально разности температур.

В соответствии с принятыми ранее допущениями можно записать условия теплового равновесия:

Где: Q – количество теплоты, которое сообщается телу за единицу времени, размерность кал/сек или дж/сек;

С – теплоемкость тела (количества тепло необходимого для повышения температуры на 1 0 ), размерность кал/град или дж/град;

А – теплоотдача (количество тепла, рассеиваемое поверхностью в секунду при разности температур тела и среды в 1 0 ), размерность кал/сек∙град или дж/сек∙град;

τ – превышение температуры тела над температурой окружающей среды;

Проинтегрировав выражение (2) получим:

Постоянную интегрирования можно найти из начальных условий: при t = 0 и τ = τ_нач, подставив которые получим:

Использовав значение постоянной интегрирования:

Отношение теплоемкости электродвигателя к его теплоотдаче назовем постоянной времени нагрева и обозначим:

В соответствии с размерностью входящих в формулу (5) величин размерность постоянной времени будет равна:

Подставив Θ в выражение (4) получим:

Полученная в результате вычислений кривая нагрева будет иметь следующий вид:

Кривая показывает, что в начальном этапе (при t = 0) начальное превышение температуры было равно τ = τ_нач. По истечению бесконечно большого времени (t = ∞) превышение температуры достигнет какого-то установившегося значения:

Используя понятия об установившейся температуре выражению можно придать вид:

Если в начальный момент времени превышение температуры тела над окружающей средой τ_нач = 0 уравнение процесса нагрева примет более простой вид:

Выражение (7) показывает, что установившаяся температура перегрева тела определяется только количеством выделяемого в теле тепла и его теплоотдачей и совершенно не зависит от теплоемкости тела. Отсюда следует, что при сохранении постоянства теплоотдачи установившаяся температура перегрева будет пропорциональна количеству тепла, сообщаемого телу.

Но с другой стороны, улучшив отвод тепла от тела (принудительное охлаждение) мы пропорционально снижаем его перегрев.

Соотношение (7) позволяет наметить основные пути, направленные к более рациональному использованию материалов при конструировании электрических машин. Правильно рассчитанный электродвигатель должен иметь при номинальной нагрузке максимально допустимую температуру перегрева изоляции:

Подставив значение потерь при номинальном режиме, выраженное через КПД и номинальную мощность, а также значение теплоотдачи и решив все относительно Р_ном получим:

Выражение (12) показывает, что для получения максимальной мощности электродвигателя необходимо иметь максимальный КПД. В этом случае потери будут сведены к минимуму. Мощность электрической машины будет больше в случае более интенсивного охлаждения и большей охлаждаемой площади. С этой целью в электрических машинах широкое распространение получили вентиляторы, которые улучшают охлаждение. Для увеличения площади охлаждающей поверхности корпус электрических машин очень часто выполняют ребристым (особенно наглядно видно на примере асинхронных электродвигателей). Также существует еще один способ повышения мощности – это повышение теплостойкости изоляции.

Формула (12) позволяет сделать вывод, что открытая машина при одинаковых габаритах будет иметь мощность больше, чем закрытая. Это связано с тем, что воздух, проходящий через внутренние части открытой машины, лучше охлаждает ее компоненты чем в закрытой, так как площадь охлаждения внешней поверхности в закрытой машине будет значительно ниже.

Для различного рода приближенных расчетов по формуле (10) удобно использовать номограмму:

Задавшись значениями Θ и t и проведя через эти точки прямую до третьей вертикали получают повышение температуры в долях установившегося перегрева тела.

Продолжим анализ выражения (10). Температура перегрева тела представляет собой сумму трех слагаемых. Соотношение этих слагаемых будут определять характер процесса. При сообщении телу какого-то количества теплоты Q, которому соответствует установившаяся температура перегрева τ_у, при τ_у> τ_нач будет иметь место нагрев тела до температуры τ_у.

В случае подведения меньшего количества теплоты Q, а именно при τ_нач> τ_у>0, произойдет понижение температуры от τ_нач до τ_у.

При отсутствии подвода тепла Q = 0 и τ_у = 0 превышение температуры будет равно:

Вследствие наличия разности температур в сторону превышения τ_нач>0 и Q = 0, тело начнет охлаждаться, то есть отдавать тепло.

Очевидно, что процесс теплообмена будет продолжатся до тех пор, пока температуры окружающей среды и тела не сравняются.

На рисунке ниже показана кривая нагрева электрической машины и ее составляющие:

Кривая τ₁ соответствует нагреву, τ₂ охлаждению при сообщении тепла, а τ₃ – охлаждение до температуры окружающей среды. Таким образом, в зависимости от значений τ_нач и τ_у можно иметь любой характер теплового процесса.

При охлаждении электродвигателя с самовентиляцией в отключенном состоянии с неподвижным якорем или ротором условия отдачи тепла будут хуже и отдача А меньше, чем в процессе работы машины. Поэтому постоянная Θ₀ = С/А будет при охлаждении больше, чем при нагреве, то есть Θ₀>Θ.

Кривая охлаждения неподвижной электрической машины приведена ниже, для сравнения там приведена и кривая нагрева:

Видео:Процессы нагрева и охлаждения потребителей электрической энергииСкачать

ТЕПЛОВОЙ РЕЖИМ И НОМИНАЛЬНАЯ МОЩНОСТЬ ДВИГАТЕЛЯ

При работе электродвигателя в нём возникают потери, на покрытие которых расходуется часть потребляемой им электрической энергии. Потери возникают в активном сопротивлении обмоток, потери стали, вызваны изменением магнитного потока в магнитопроводе, механические потери на трение в подшипниках и трение о воздух вращающихся частей машины. В конечном итоге вся энергия потерь превращается в тепловую энергию, рассеивающуюся в окружающей среде. Потери в двигателе бывают постоянные и переменные. К постоянным относятся потери в стали и механические потери, ко вторым ─ потери в обмотках двигателя. Потери, возникающие в обмотках двигателя, вызывают его нагрев.

В начальный период после включения двигателя большая часть выделяющегося в двигателе тепла идёт на повышение его температуры, а меньшая отдаётся в окружающую среду. Затем по мере увеличения температуры двигателя всё большее количество тепла передаётся в окружающую среду, и наступает момент, когда всё выделяемое тепло рассеивается в пространстве. Тогда наступает тепловое равенство и дальнейшее повышение температуры двигателя прекращается. Такая температура нагрева двигателя называется установившейся; она с течением времени остаётся постоянной, если нагрузка двигателя не изменяется. Количества тепла Q, которое выделяется в двигателе за 1сек. Можно определить по формуле

(340)

Где :

Р₂ – мощность на валу двигателя.

Из выражения (340) следует, что чем больше нагрузка двигателя, тем больше тепла в нём выделяется и тем выше его установившаяся температура.

Наиболее чувствительным к нагреву элементом двигателя является изоляция обмоток, огранивающая температуру нагрева двигателя, а следовательно, и использование его мощности. Так, двигатель с обмоткой в хлопчатобумажной изоляции при нормальной нагрузке и температуре нагрева 100 о С может работать 15 – 20 лет; при температуре на 25% температура нагрева обмотки повышается до 145 о С и двигатель выйдет из строя уже через 1,5 месяца: при перегрузке на 50% температура обмотки составит 225 о С и она разрушится примерно через 3ч. работы двигателя.

Согласно ГОСТ8865 – 58 изоляционные материалы, используемые в электромашиностроении, по нагревостойкости делятся на семь классов, для каждого из которых устанавливается максимально допустимая температура (табл. 1).

Характеристика материала	Класс нагревостойкости	Предельно допустимая температура С о
Непропитанные хлопчатобумажные ткани, пряжа, бумага и волокнистые материалы из целлюлозы и шёлка	y
Те же материалы, но пропитанные связующие	A
Некоторые синтетические органические плёнки	E
Материалы из слюды асбеста и стекловолокна, содержащие органические связующие вещества	B
Те же материалы в сочетании с синтетическими связующими и пропитывающими составами	F
Те же материалы, но в сочетании с кремний органическими связующими и пропитанными веществами	H
Слюда, керамические материалы, стекло, кварц, асбест, применяемые без связующих составом или с органическими связующими составами	C	Более 180

Допустимые превышение температуры обмотки двигателя над температурой окружающей среды (в СССР принято +35 о С) для класса нагревостойкости y составляет 55 о С; для класса А – 70; для класса В – 95; для класса С – более145 о С. Превышение температуры данного двигателя зависит от величины его нагрузки и режима работы. При температуре окружающей среды ниже 35 о С двигатель можно нагрузить выше его номинальной мощности, но так, чтобы при этом температура перегрева изоляции не превышала допустимой нормы.

Исходя из известного количества тепла Q, выделенного при работе двигателя, можно подсчитать превышение температуры двигателя t о С над температурой перегрева

_о (341)

где: А – теплоотдача двигателя, кал/град · сек;

e – основание натуральных логарифмов (e=2,718);

С – теплоёмкость двигателя, кал/град;

t_о – начальное превышение температуры двигателя при t = о;

Установившаяся температура t_у двигателя может быть получена из предыдущего выражения, если принять t =¥. Тогда . При _о =о равенство (341) примет вид

(342)

Обозначим отношение через Т, тогда

, (343)

где: Т – постоянная времени нагрева, сек.

Кривая нагрева, постоянная по уравнению, показана на рис. 61,а.

Постоянная времени нагрева — это время, в течении которого двигатель нагрелся бы до установившейся температуры при отсутствии теплоотдачи в окружающую среду. При наличии теплоотдачи температура нагрева будет меньше и равна 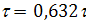_у. Постоянная времени может быть найдена графически. Для этого из начала координат проводят касательную ос до пересечения с горизонтальной прямой, проходящей через точку a, соответствующую температуре установившегося нагрева. Отрезок bc будет равен Т, а отрезок ab – времени , в течение которого двигатель достигает установившейся температуры . Обычно принимают равным 4Т.

Постоянная времени зависит от номинальной мощности двигателя, скорости его вращения, конструкции и способа охлаждения, но не зависит от величины его нагрузки.

Если двигатель после того, как он нагреется, отключить от сети, то, начиная с этого момента, он уже не получает тепла, а накопленное в его частях тепло продолжает рассеиваться в окружающей среде и двигатель охлаждается.

Уравнение охлаждения имеет вид

(344)

а кривая показана на рис. 61, б. В выражении (344) Т_о — постоянная времени охлаждении. Она отличается от постоянной времени нагрева Т, так как теплоотдача двигателя, находящегося в покое, отличается от теплоотдачи работающего двигателя. Равенство Т_о = Т возможно лишь в том случае, когда двигатель, отключенный от сети, продолжает вращаться или имеет постороннюю вентиляцию. Обычно кривая охлаждения идет более полого, чем кривая нагрева. У двигателей с внешним обдувом Т_о, больше Т примерно в 2 раза, у двигателей открытого типа — в 3 раза, а у двигателей закрытого типа с естественным охлаждением постоянные времени Т и Т_о примерно равны. Практически можно считать, что через промежуток времени, равный от 3 до 5 Т_о, температура двигателя становится равной температуре окружающей среды.

Рис. 61. Кривые нагревания и охлаждения электродвигателя:

а — графическое определение постоянной времени; б – кривые нагревания и охлаждения;

в – кривые нагревания двигателя при различных нагрузках

При правильном выборе номинальной мощности двигателя установившаяся температура перегрева τ_у должна быть равна допустимому превышению температуры τ_доп соответствующему классу изоляции обмоточного провода. Различным нагрузкам Р₁

Исходя из изложенного, можно дать следующее определение номинальной мощности двигателя. Номинальная мощность двигателя представляет собой мощность на валу, при которой температура его обмотки превышает температуру окружающей среды на величину, соответствующую принятым нормам перегрева

ЧТО И КАК ПИСАЛИ О МОДЕ В ЖУРНАЛАХ НАЧАЛА XX ВЕКА Первый номер журнала «Аполлон» за 1909 г. начинался, по сути, с программного заявления редакции журнала.

Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам.

Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все.

Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право.

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте: