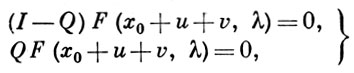Теория ветвления решений нелинейных уравнений

ВЕТВЛЕНИЕ РЕШЕНИЙ нелинейных уравнений — явление перехода нек-рого решения нелинейного уравнения в несколько решений (пли полное его исчезновение) при малых изменениях параметров. Более точно, пусть нелинейное уравнение

с (не обязательно числовым) параметром λ имеет при фиксированном значении λ₀ решение х₀. Тогда при значениях λ, близких к λ₀, уравнение (*) может иметь несколько (более одного) решений х(λ), близких к х₀. В этих случаях говорят, что происходит ветвление решения х₀, а пара (х₀, λ₀) наз. точкой ветвления уравнения (*).

Пример: Уравнение х 2 — λ = 0, где х и λ — комплексные переменные, имеет точку ветвления (х₀, λ₀) = (0, 0), ибо существует двузначное решение х = √λ, т. е. решение х = 0 (при λ = 0) разветвляется при малых λ ≠ 0 на два малых нетривиальных решения.

Современная теория В. р. основывается на идеях А. М. Ляпунова [1] и Э. Шмидта [2] и наиболее развита для нелинейных уравнений в банаховых пространствах.

Пусть Е₁ и Е₂ — комплексные банаховы пространства, x ∈ E₁, λ — комплексное переменное, a F(x, λ) -нелинейный оператор, непрерывный вместе с Фреше производной F_x(x, λ) в окрестности Ω точки (х₀, λ₀), отображающий Ω в окрестность нуля пространства Е₂ и такой, что F(x₀, λ₀) = 0, a F_x(x₀, λ₀) ≡ В — Фредгольма оператор.

Задача состоит в том, чтобы найти в шаре ||х — х₀|| -1 , то задача имеет единственное решение х(λ), причем х(λ₀) = х₀. Если же В -1 не существует, то нуль-пространство N(В) оператора В имеет размерность n ≥ 1. В этом случае задача может быть сведена к аналогичной конечномерной задаче. Пусть через Р обозначен проектор Е₁ на N(В), а через I — Q — проектор Е₂ на область значений оператора В, где I — тождественный оператор. Уравнение (*) может быть записано в виде системы

где u = (I — P)(x — x₀), v = P(x — x₀). Из первого уравнения системы определяется неявный оператор u = f(v, λ). В результате его подстановки во второе уравнение системы получается уравнение

для определения v; оно наз. уравнением разветвления. Полное решение задачи о нахождении в шаре ||v||

Видео:После этого видео, ТЫ РЕШИШЬ ЛЮБУЮ Систему Нелинейных УравненийСкачать

Диаграмма Ньютона и ветвление решений

Нелинейных уравнений

В этом параграфе рассмотрены особые случаи задачи о не­явных операторах. Пусть нелинейное уравнение F(x, Х)= 0 с параметром X имеет при фиксированном значении параметра Хо решение хо. Если при значениях X, близких к А,₀, это уравнение имеет несколько (более одного) решений х(>»), близких к хо, то говорят, что происходит ветвление решения .vo.

Современная теория ветвления решений нелинейных уравне­ний (см. [2]) основывается на идеях А. М. Ляпунова и Э. Шмидта и широко использует методы функционального ана­лиза. В одномерном случае, который здесь рассматривается, важную роль играет метод диаграммы Ньютона. С помощью этого метода решаются, впрочем, и некоторые другие матема­тические проблемы.

37.1. Метод диаграммы Ньютона. Пусть комплекснозначная функция f(x,X) комплексных переменных х и X представляет со­бою многочлен степени л относительно х:

где, согласно определению многочлена степени л, /_Л(Я)#0. От­носительно коэффициентов f_s(X) мы сделаем довольно слабые предположения. Пусть они представимы в окрестности точки А = 0 в виде сходящихся рядов:

где p_s — рациональные числа, а р— общее для всех f_s нату­ральное число.

Заметим, что если при некотором s f_s(k0, то можно счи­тать, что j₀s Ф 0. Будем далее считать, что ыФ 0, т. е. f(0,Я) Ф Ф-Q. Будем разыскивать решения х = х(Х) уравнения

где f определена равенствами (1), (2), представимые в виде

л: = + х, (4)

где х_гф 0, а Х=0<Я е ) при Я->0. Чтобы найти возможные значения показателя е и коэффициента х_е, нужно подставить (4) в (I) и приравнять нулю главный член, т. е. коэффициент при наинизшей степени Я. Однако, пока показатель е остается неизвестным, нельзя сказать, какие из членов (после этой под­становки) будут низшими. Ясно только, что члены наинизшего порядка содержатся среди следующих:

/оо* 00 . L*> 0k+ke > (5)

где к пробегает те из значений 1, 2, . л— 1, для которых f_k(Х)Ф 0. Так как /₀о Ф 0 и f_0n Ф 0, то отличны от нуля по мень­шей мере два члена в (5).

Для уничтожения члгнов наинизшего по Я порядка необхо­димо подобрать показатель е так, чтобы по крайней мере два из показателей р₀, р* + кг, р_л + ле совпали, а остальные были не меньше их. Это соображение позволяет отыскивать все воз­можные значения е и соответствующие им значения коэффи­циента х_е.

Для нахождения значений е используется диаграмма Нью­тона. Нанесем в декартовой прямоугольной системе координат точки (рис. 22) (0, р₀), (k, рО, (л, р„), где k пробегает те же значения, что ив (5). Проведем в точке (0, ро) прямую так, чтобы она совпала с осью ординат, и станем ее вращать вокруг точки (0, ро) против часовой стрелки до тех пор, пока на нее впервые не попадет другая из нанесенных точек, например _t(l, pi). Тангенс угла между этим положением прямой L и отрицательным направлением оси абсцисс равен одному из воз­можных значений е, ибо tg а = (ро — pi) /1-е. Если под таким углом провести прямые через точки (s,p_s), отличные от попав­ших на L, то эти прямые будут лежать выше L, а потому ps + ss > pt -f- 1г.

Отметим, что на прямой, соединяющей точки (0, ро) и (/, р/), могут оказаться и другие точки (k, рь). Будем теперь вращать прямую L в том же направлении вокруг той оказавшейся на прямой L точки (/, р;), у которой абсцисса наибольшая, пока на L не попадет другая из нанесенных точек, например (р, р_Р). Тангенс угла между новым направлением прямой L и отрица­тельным направлением оси абсцисс определит другое возмож­ное значение е:

ибо прямые, проходящие через другие точки (s, p_s) параллельно этому новому направлению L, будут лежать выше, а значит, pi + es > pi -f el = p_p + ер. Продолжая этот процесс, получим всевозможные значения е. Выпуклая ломаная, соединяющая точки поворота прямой L, называется диаграммой Ньютона.

Перейдем к определению возможных значений коэффициен­тов х_е. Пусть (/, р,) и (J, р/) — крайние точки одного из звеньев диаграммы — отрезка, определяющего одно из возможных зна­чений е. Для того чтобы после подстановки (4) в (3) уничто­жились низшие члены, необходимо и достаточно, чтобы

s

где знак штрих у суммы здесь означает, что суммирование про­водится по s, удовлетворяющим соотношению p_s + se = р е в разложе­нии (4).

Для нахождения следующего члена разложения у нужно подставить (4) в (3) и тем же приемом определить низший член разложения, полагая

Х = хА г ‘ + О (X е ‘).

Продолжая этот процесс, можно показать (строгие формули­ровки и доказательства см. в [2], § 2), что все п решений урав­нения (3) имеют вид (ряды Пюизо)

х = х_еХ г + луА е + лг_е»А е + . (7)

Отметим, далее, что диаграмма, построенная для определе­ния первого показателя е, имеет общую длину звеньев, рав­ную п. Она разбивается в общем случае на три участка: убы­вающий, постоянный и возрастающий. Убывающий участок (в наших предположениях он существует) определяет поло­жительные значения показателей е и, значит, приводит к опреде­лению решений уравнения (3) таких, что х(0) = 0. Постоянный участок диаграммы соответствует значению е = 0 и определяет, согласно (4), неявные функции х = х(Я) вида х(я) = хо + о(1) при Я —> 0, где Хо ф 0. Наконец, возрастающий участок диаграм­мы Ньютона приводит к опреде­лению так называемых «боль­ших решений» уравнения (3), стремящихся к бесконечности при Я- чения показателя е отрицательны.

37.2. Примеры на определение неявных функций с помощью диаграммы Ньютона. Приведем несколько примеров, иллюстри­рующих метод.

Пример 1. Рассмотрим следующее кубическое уравнение с малым параметром Я:

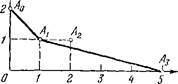
(— Я + Я 2 ) + х (1 + Я-Я 2 ) + х 2 (- 1 — Я 2 + Я 3 ) + х 3 Я = 0. (1) Выберем декартову прямоугольную систему координат. По оси абсцисс будем откладывать значения показателей k степеней х в уравнении (1), а по оси ординат будем откладывать значения показателей р_й степеней Я в этом же уравнении (рис. 23).

Построим точки Л₀ = (0, 1), А =(1,0), Л₂ = (2,0), Л₃ = = (3,1). Выпуклая ломаная, соединяющая последовательно эти точки, и является, согласно п. 37.1, диаграммой Ньютона урав­нения (1). Ее убывающее звено — отрезок, соединяющий точки Л₀ и Ль — соответствует значению е=1 и определяет един­ственное решение Х1(Я) уравнения (1), аналитическое при X = 0, такое, что х(0)= 0, согласно теореме п. 36.5. При этом х,(Я)= Я + о(Я).

Постоянное звено диаграммы — отрезок, соединяющий точки А у и Л₂,— определяет неявную функцию х(Я), удовлетворяю­щую условию х₂(0) = 1, также аналитическую при к = 0, так что

Наконец, возрастающая часть диаграммы также состоит из одного звена — отрезка, соединяющего точки А₂ и Л₃. Этому отрезку отвечает значение е = —1 и «большое» решение х₃(Я) уравнения (1):

Упражнение 1. Покажите, что х₃(Я) разлагается в схо­дящийся в окрестности точки л = 0 с выколотой точкой % = О ряд Лорана

Указание. Воспользуйтесь замечанием п. 37Л и просто­той соответствующего корня уравнения (6) п. 37Л.

г И

Рис.23. Рис. 24.

Упражнение 2. Найдите с точностью О (к) решения х, (к), /=1,2,3, уравнения (1).

Итак, все три решения уравнения (I) можно найти методом диаграммы Ньютона. Пример 2. Пусть

/ (х, Я) = Я 2 — Ях 2 — Ях 3 + х 5 = 0. (2)

Построим точки А₀ = (0, 2), А — (2, 1), Л₂ = (3, 1), Л₃ = (5,0) (рис. 24). Диаграмма Ньютона имеет только убывающую часть и состоит из двух звеньев — отрезка А_йА и отрезка Л]Л₃. Им отвечают два значения е: е=1/2 и е = 1/3. Полагая в (2) х = х,_/2Я 1/2 + X_lf2(k), получаем для определения х_х/2 уравнение 1 — x_j2 = 0,откуда ху, = ±1, причем оба корня простые. Ана­логично, полагая в (2) х = х 1/зЯ 1/3 + Х_1/3(к), приходим к урав­нению — х 2 _/3 + Х[_/3 = 0. Это уравнение имеет три ненулевых

простых корня xi/3 = -v^l . Итак, уравнение (2) определяет дву­значную неявную функцию

и трехзначную неявную функцию

оо

Упражнение 3. Покажите, что при Я>0 уравнение (2) имеет два вещественных решения вида (3) и одно веществен­ное решение вида (4).

Упражнение 4. Найдите вещественные решения уравне­ния (2) при Я 2 — 2кх -f А 2 — ж 3 = 0. (5)

Упражнение 5. Покажите, что уравнение f(x, Я) = 0 имеет решение вида х(к) = Я + о(Я), причем 1—двукратный корень определяющего уравнения.

Для нахождения следующего члена х(к) полагаем в (5) х = Я + и. После уничтожения подобных членов получаем для определения и уравнение

и 2 — Я 3 — ЗЯ 2 ы — ЗЯы 2 — и 3 = 0.

Упражнение 6. Постройте диаграмму Ньютона для этого уравнения и покажите, что и = Я 3/2 , причем 1 — простой корень определяющего его уравнения. Таким образом, уравне­ние (5) имеет двузначное решение вида

*(Я) = Я + Я 3/2 + Т,х_кк щ . (6)

Упражнение 7. Покажите, что в вещественном случае при Я > 0 уравнение (5) определяет два решения вида (6), а при Я 1

и пусть числа г> 0 и р>0 таковы, что при сходится, мажорирующий ряд (1), числовой ряд

£ fi,r l p’.(2)

Нашей целью является локальное определение непрерывных неявных функций х = х<Х)— решений уравнения

удовлетворяющих условию х <0)=0. Ниже такие неявные функ­ции мы будем называть малыми решениями уравнения (3).

Случай, когда /ю = fx (0, 0) ф 0, уже рассмотрен нами в тео­реме п. 36.5. Согласно этой теореме уравнение (3) имеет един­ственное малое решение, аналитическое в точке X = 0; значит, представимое сходящимся рядом

с ненулевым радиусом сходимости.

Ниже мы предполагаем, что /ю = 0. Это означает, что мы не можем воспользоваться теоремой о неявных операторах п. 36.5. Уравнение (3) принимает теперь следующий вид:

Естественно предположить, далее, что найдется номер п та­кой, что

В противном случае уравнение (5) можно сократить на X, и если fa ф 0, то оно малых решений не имеет. Если же/oi = 0, то после сокращения на X мы снова получим уравнение типа (4).

Оказывается, что в предположении (6) уравнение (5) имеет ровно п, с учетом кратности, малых решений и все они предста- вимы сходящимися рядами по целым или дробным степеням параметра X. Доказательство этого утверждения может быть проведено с помощью так называемой подготовительной тео­ремы Вейерштрасса. Согласно этой теореме, в сделанных нами относительно f(x,X) предположениях, в окрестности точки (0, 0) эта функция может быть представлена в виде

где q(x,X)—аналитическая в (0,0) функция, причем п + р_п_ ,(*, X)

с аналитическими при Я = 0 коэффициентами, удовлетворяю­щими условиям pk(0) = 0, k = 0, 1, . п—1. Из (7) видно, что малые решения уравнения (5) и малые решения уравнения

совпадают. Но тогда, согласно методу диаграммы Ньютона (см. п. 37.1), уравнение (8), а с ним и уравнение (5), имеет п ма­лых решений, представпмых сходящимися рядами по целым или дробным степеням Я.

Для практического нахождения малых решений уравнения (5) нет необходимости переходить, к представлению (7). Можно применить метод диаграммы Ньютона непосредственно к урав­нению (5). В этом случае диаграмма может состоять из счет­ного числа отрезков. Однако поскольку нас интересуют лишь малые решения уравнения (5), то мы должны рассмотреть только убывающий участок диаграммы Ньютона, который всег­да состоит из конечного числа звеньев.

Упражнение. С помощью метода диаграммы Ньютона найдите все малые решения уравнения

sin х — х -f х 2 sin Я — Я 4 = 0.

Указание. Воспользуйтесь тейлоровским разложением си­нуса.

37.4. Точки ветвления и точки бифуркации. Продолжим ис­следование уравнения (1) п. 36.1

в предположении, что

Пусть оператор F определен на множестве Q, Q(х₀, Я₀) 0 и р > 0 такие, что при каж­дом Яе5р(Яо) существует единственное решение х = х(Я)е eS,(*о) уравнения(1), то точку (а’о, Яо) будем называть регу­лярной точкой этого уравнения. Теоремы о неявных операторах дают условия, достаточные для регулярности точки (хо, Яо).

Среди нерегулярных точек важное место занимают точки ветвления.

Определение 1. Точка (хо, Я₀) называется точкой вет­вления уравнения (1), если для любых г>0 и р>0 найдется Яе5р(Яо), которому отвечают по крайней мере два решения уравнения (1), лежащих в шаре Sr(x₀).

Приведем простейшие примеры точек ветвления.

Пример 1. Для уравнения х 2 — Я = 0 в комплексном слу­чае точка (0, 0) является точкой ветвления, так как уравнение определяет в ее окрестности двузначную неявную функцию

х— д/я ._Это верно и в вещественном случае, где два решения х = ± д/Я определены при Я > 0.

Пример 2. Пусть X = Y — С[—1,+1], Л = £> (рассмат­ривается вещественный случай). Покажем, что для интеграль­ного уравнения

1 1 x(t) = sx 2 (s)ds (3)

точка х = 0, Я = 1/2 является точкой ветвления. В самом деле,

из (3) следует, что x(t)= Ха Ц- Ь, где а — ^ х (s) ds, b = ^ sx 2 X

-i -i «X(s)ds. Интегрируя на [—1,1] x(() и tx 2 <t),получим систему уравнений

а = 21а + 26, 6= 0.

Если Хф!2, то а = 0, откуда .*■(/) s=0. Если же Я =1/2, то а произвольно. Итак, уравнение (3) при всех X имеет три­виальное решение, а при X, = 1/2 решением (3) является также функция x(t)^= с, где с — произвольная постоянная. Поскольку при X — 1/2 уравнение (3) имеет бесчисленное множество ре­шений, точка (0, 1/2) является точкой ветвления этого уравне­ния.

Пример 3. Интегральное уравнение

1 1 x(i) = x_jx(s)ds+ J x 2 (s)ds о о

имеет два решения: х(/) = 0 и *(/)= 1 —X. Следовательно, точ­ка (0, 0) является его точкой ветвления.

Вернемся к уравнению (1). Пусть теперь f(0, Я) = 0. Определение 2. Точка Хо называется точкой бифуркации уравнения (1), если точка (0, Яо) является точкой ветвления этого уравнения.

Примеры 2 и 3 дают, очевидно, примеры точек бифуркации. 37.5. Уравнение разветвления Ляпунова — Шмидта. Предпо­ложим здесь, что оператор F(x,X) непрерывен в £2(дго, Яо) и что он имеет в Q(*o, Яо) непрерывную частную производную F_x(x, Я). Пусть, далее, оператор А ——F_x(x ₀, Я₀) фредгольмов, причем п = &m N1 (N(А)—подпространство нулей А, см.§ 21). Для изучения уравнения (1) с условием (2) п. 37.4 запишем это уравнение в виде

Пусть ? — базис в N (А), » — биортогональная к нему система из Х* пусть, далее, — базис в N (A*), a fo>? — биортогональная к нему система элементов из Y. Введем линей­ный оператор

В = А + К, где К=Z 41 как параметр, можно применить теорему п. 36.3 о неявных опе­раторах. Однако удобнее сначала немного преобразовать это уравнение. А именно положим в (2)

u = v + £ ьчч. (4)

Поскольку Вф; = г,, i — 1,2. я, подстановка (4) в (2) при­водит к уравнению

Это уравнение имеет при всех достаточно малых р, gi, . единственное малое решение у = у(р, £i £„). Следователь­но, уравнение (2), в соответствии с (4)> имеет единственное ма­лое решение

Это решение должно также удовлетворять уравнениям (3).Учи­тывая условия биортогональности = 8i/, мы получаем для определения |ь . |_л следующую систему уравнений:

Эта система называется уравнением разветвления Ляпунова — Шмидта. Нетрудно показать, что формула (6) устанавливает взаимно однозначное соответствие между малыми решениями уравнения (1) и системы (7).

Придадим теперь уравнению разветвления (7) другую, бо­лее удобную форму.

В п. 21.4 мы установили, что

где черта означает комплексное сопряжение. Отсюда, вслед­ствие биортогональности = 6,/, имеем К*Ф/=)’/ (про­верьте!). Следовательно, так как е N(A*),

= (А»+ /Г)Ч>/ = Г+/ = V/, /= 1. л- (8)

Применяя к обеим частям уравнения (5) функционал ‘Фа, полу­чаем с помощью формул (8)

Обращаясь к системе (7), мы видим теперь, что ее можно ваписать в такой форме:

С учетом формул (6) получаем окончательно

Напомним, что функция ц(р, £ь . |„) определяется как малое решение уравнения (2).

37.6. Исследование задачи о ветвлении в одномерном ана­литическом случае. В этом пункте мы предположим дополни­тельно, что оператор F(x,X) аналитичен в точке (*оДо), т. е. разлагается вблизи (х₀, Ао) в степенной ряд (F(x₀, А₀) = 0)

Далее, предполагается, что п = dim N(A) = 1. Положим ф! = ф, 2i = 2, ^ = 1. Уравнение (2) п. 37.5 здесь при­

Положим В- 1 = Г и будем искать малое решение уравнения (1) в виде

£ (2)r+s^l

Чтобы получить уравнение разветвления, мы должны подста­вить этот ряд в уравнение (9) п. 37.5, которое здесь выглядит так: , (

Подстановка (2) в (3) приводит к следующему уравнению:

Таким оЗразом, уравнение разветвления Ляпунова — Шмид­та в рассматриваемом случае совпадает с уравнением (5) п. 37.3 и может быть исследовано с помощью метода диаграммы Нью­тона. Возможен, впрочем, и вырожденный случай, когда /oi = 0. fti = 0, i + j ^ 2. В этом случае в качестве | = |(р) можно взять любую функцию к. Если же выполнено условие (6) п. 37.3, то уравнение (3) имеет ровно п, с учетом их кратности, малых решений, причем все они разлагаются в сходящиеся ряды по целым или дробным степеням параметра ц. Но тогда это заклю­чение верно и для исходной задачи.

Коэффициенты уравнения разветвления (4) можно подсчи­тать с помощью (1), (2), (3).

Упражнение 1. Покажите, чго ию = Г2 = 2 , (6)

Здесь х = С 2 [0, я] — вещественное пространство дважды не­прерывно дифференцируемых на [0, я] функций, удовлетворяю­щих граничным условиям (7), А = Е У = С[0, л]. Можно принять ф = if> = 2 = y = s ‘ n t-

Далее, главные коэффициенты уравнения разветвления (3) имеют вид (см. (5))

л

/oi = (sin/, ф) = ^ sin 2 tdt = -^-, о

л

Следовательно, убывающая часть диаграммы Ньютона состоит из одного отрезка, соединяющего точки (0, 1) и (2,0), так что

6 = 1/2 и x = x_mW’ 2 +о(ц ! ‘ 2 ).

Для определения х_1/г получаем уравнение f₀₁ + = О, откуда х_щ = ± . Итак при р > 0 задача (6) — (7) имеет

два малых решения вида

Эти решения аналитичны относительно переменной Viu

Упражнение 2. Найдите точки бифуркации краевой за­дачи и главные члены ее решений

-х» + Хх = х 3 , х(0) = х(п) = 0.

Упражнение 3. Найдите главные члены малых решений интегрального уравнения

Видео:Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать

Ветвление решений нелинейных уравнений в пространствах функций на многообразиях Текст научной статьи по специальности « Математика»

Видео:Нелинейные уравнения с двумя переменными и их геометрический смысл. 9 класс.Скачать

Аннотация научной статьи по математике, автор научной работы — Эргашбаев Т.

В статье приводится общая постановка задачи теории ветвления нелинейных уравнений , инвариантных относительно некоторой группы симметрии.

Видео:Математика это не ИсламСкачать

Похожие темы научных работ по математике , автор научной работы — Эргашбаев Т.

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Branching off the solution of non-linear equitation in space functions of diversities

The article deales with the description of theory of branching off non-linear equations which are the invariants towards some groups of symmetry. Equation of the branching off the groups SO(2) and O(2) have also been studied.

Видео:Методы численного анализа - Метод Ньютона, секущих для решения систем нелинейных уравненийСкачать

Текст научной работы на тему «Ветвление решений нелинейных уравнений в пространствах функций на многообразиях»

ДОКЛАДЫ АКАДЕМИИ НАУК РЕСПУБЛИКИ ТАДЖИКИСТАН _2014, том 57, №5_

ВЕТВЛЕНИЕ РЕШЕНИЙ НЕЛИНЕЙНЫХ УРАВНЕНИЙ В ПРОСТРАНСТВАХ

ФУНКЦИЙ НА МНОГООБРАЗИЯХ

Худжандский государственный университет им. академика Б.Гафурова

(Представлено членом-корреспондентом АН Республики Таджикистан З.Х.Рахмоновым 16.01.2014 г.)

В статье приводится общая постановка задачи теории ветвления нелинейных уравнений, инвариантных относительно некоторой группы симметрии.

Ключевые слова: уравнение разветвления — инвариантность — группа — бифуркация — действие группы — нелинейное уравнение.

Общая задача теории ветвления (теории бифуркации) в банаховых пространствах заключается в следующем:

Рассматривается операторное уравнение

где Ф — оператор, непрерывно зависящий от параметра Л. Требуется описать множества решений

уравнения (1), близких к заданному решению (х0, Л) . Если Ф — нётеров оператор, то для описания

такого множества уравнения (1) с помощью конструкции Ляпунова-Шмидта заменяется уравнением разветвления:

где у — элемент пространства кег В, здесь В означает линейную часть оператора Ф в точке х0.

Оказывается, что если оператор Ф инвариантен относительно некоторой группы Ли, то в определённых условиях вместо уравнения (2) можно написать уравнение

где у — элемент некоторого подпространства в кег В. Таким образом, исследование уравнения (1) сводится к исследованию уравнения (3), которое зависит от меньшего числа вспомогательных параметров.

Уравнение ф (у, /I) = 0, заданное в области конечномерного пространства V х Л0, называется редуцированным уравнением для исходного уравнения (1). Таким образом, получается конечное число уравнений, зависящих от конечного числа параметров. При этом исходный оператор может не

Адрес для корреспонденции: Эргашбаев Т. 735700, Республика Таджикистан, г. Худжанд, проезд Мавлянбеко-ва 1, Худжандский государственный университет. E-mail: abulkosim-m@mail.ru

быть нётеровым, так как его ядро может быть бесконечномерным, если банахова группа имеет бесконечную размерность.

Определение: Действием группы на многообразии X называется отображение ж : X х О ^ X, подчиненное условиям:

1) ж(х,е) = х, 2) ж(х, gh) = ж(ж(x, g), к),

где е — единица группы.

Образ элемента (х, g) при отображении ж обозначим через gx . Множество g е О>

называется орбитой точки х0. Действие группы дифференцируемо, если дифференцируемо отображение ж. Если X = Е — банахово пространство, то отображение ж будем обозначать Ь ■ Рассмотрим задачу о точке бифуркации

Вх = Я (х, к), Я (0,к) = 0, Ях (0,0) = 0 (4)

В : Е ^ Е — линейный нётеров ограниченный оператор с й -характеристикой (п, т), Я (•, к) -нелинейный оператор, определённый в окрестности нуля пространства Е1. Пусть уравнение (4) допускает группу О , то есть существуют её представления Ь и К в пространствах Е1 и Е2 соответственно такие, что для любого g е О;

В^х = КВ, Я (LgX, к) = КЯ (х, к) .

Тогда подпространство кег В инвариантно относительно операторов , а 1т В — относительно К . Предположим выполненным

Условие: существует прямое дополнение Е» п к ядру оператора В, инвариантное относительно представления Ь .

Нелинейное функциональное уравнение может быть задано на £ -мерном компактном многообразии V с краем йу или без края в (£ +1) -мерном пространстве Я£+1. Если V имеет край, то к

уравнению следует добавить краевое условие. Как правило, соответствующие нелинейные операторы, определённые в функциональных пространствах, на многообразиях допускают группу симметрии многообразий и некоторую её часть. При изучении ветвления решений таких уравнений мы будем использовать элементы группового анализа. Приведём вначале простые примеры, первый из которых заимствован из работы [1].

Пусть уравнения ^ = ^ (^,т2) = 0, i = 1,2 допускают группу вращений плоскости Я2

Теорема 1. Двумерное аналитическое уравнение с симметрией SO (2) имеет вид:

ч (^, ^) = ЕCk (т12+т22) (^со55 а — ^ ^п а) =0,

Ч (^ ) = Е Ck (Т12 + Т22 )(*! sinаk + ^ СО^ ) = 0

В случае симметрии О (2) (дополнительная инвариантность относительно отражения J (г1, г2) = (г1, — г2) в (6)) ак = 0 при всех к .

Согласно общей теории группового анализа [2], выписываем инфинитезимальный оператор группы преобразований (5):

v „ , д д д д Х, T = —г2-+ r—t2-+ tx-

V ) дтх дт2 д ^ д tl

Переходя к полярным координатам r = r cosp, r2 = r sinp, r = ^ cosp +12 sinp ,

rp = —1 sin p +12 cosp , находим Х =-. Следовательно, Ix = r = *Лтх +T2, I2 = tr, I3 = t обра-

зуют полную систему функционально независимых инвариантов. Поскольку r = 1, редуцированное уравнение записывается в виде tr = U (r) = 0, t^ = V (r) = 0, откуда в силу аналитичности t (r, r) получаем (6).

В дальнейшем удобнее выполнять подобные рассуждения в комплексных переменных

=^ (Г1 + ir2 ) , t) = ^2 «r2t1. /3 (t) = t12 -t:

Так как г = 1, по теореме Л.В.Овсянникова получаем редуцированные с помощью инвариантов уравнения

Z1t2 -T2t1 = (Z -Т22 ) >

откуда методом неопределённых коэффициентов определяется уравнение разветвления. Если использовать другую систему инвариантов

I1 (Z) = Z — Z2, /2 (z>t) = ^2 — Z2 t1 , h (z> t) = — Z2 t2 ,

то приходиться исключать особое инвариантное многообразие zf — г2 = 0.

Поступило 16.01.2014 г.

1. Логинов Б.В., Рахматова Х.Р., Юлдашев Н.Н. — Уравнения смешанного типа и задачи со свободной границей. — Ташкент: Фан, 1987, с. 183-195.

2. Овсяников Л.В. Групповой анализ дифференциальных уравнений. — М.: Наука, 1978, 400 с.

3. Эргашбаев Т.С. — Успехи мат. наук, 1984, т.39, № 6, с. 213-214.

ШОХАРОНИИ Х,АЛЛХ,ОИ МУОДИЛА^ОИ ГАЙРИХАТТЙ ДАР ФАЗО^ОИ

ФУНКСИЯ^О ДАР БИСЁРШАКЛА^О

Донишгохи давлатии Хуцанд ба номи академик Б.Рафуров

Дар макола гузориши умумии масъалаи шохаронии даллдои муодиладои гайрихаттй нисбат ба гуруди симметриядо инвариантй оварда шуда, муодилаи шохаронии гуруддои SO (2)

ва O (2) ба вучудоварда омухта мешавад.

Калимацои калидй: муодилаи шохаронй — инвариантй — гуру% — бифуркатсия — таъсири гуру% -муодилаи гайрихаттй.

BRANCHING OFF THE SOLUTION OF NON-LINEAR EQUITATION IN SPACE

FUNCTIONS OF DIVERSITIES

B.Gafurov KhujandState University The article deales with the description of theory of branching off non-linear equations which are the invariants towards some groups of symmetry. Equation of the branching off the groups SO(2) and O(2) have also been studied.

Key words: Branching off — equation — invariant — group — bifurcation — group action — nonlinear equation.

🔥 Видео

Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать

1 3 Решение нелинейных уравнений методом простых итерацийСкачать

4.2 Решение систем нелинейных уравнений. МетодыСкачать

ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

МЗЭ 2021 Лекция 11 Метод Ньютона для решения систем нелинейных уравненийСкачать

СИСТЕМА УРАВНЕНИЙ нелинейных 9 класс алгебраСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Нелинейные уравнения. Практическая часть. 9 класс.Скачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Как решают уравнения в России и США!?Скачать

Как решать Диофантовы уравнения ★ 9x+13y=-1 ★ Решите уравнение в целых числахСкачать

15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

НЕПОМНЯЩИЙ ⚔️ ЛИЖЭНЬ! Абдусатторов Борется за Лидерство | Супертурнир в Вейк-ан-Зее 2024 | Тур 9Скачать

Как решать уравнения и неравенства? | Ботай со мной #072 | Борис Трушин |Скачать