Количественная зависимость константы скорости реакции от температуры была впервые предложена тоже Я.Вант-Гоффом (1887) в виде уравнений изохоры и изобары химической реакции (см. п. 4.5.2).
Эта идея была развита С.Аррениусом (1889), который открыл, что температурную зависимость скорости многих реакций можно описать уравнением:
k = Ае — Е* / RT
где k — константа скорости, e — основание натуральных логарифмов, R — универсальная газовая постоянная, T – температура, А — предэкспоненциальный множитель, Е* — энергия активации реакции.
Чтобы выяснить физический смысл величин А и Е*, входящих в уравнение Аррениуса, следует сначала познакомиться с основными положениями теории активных соударений(столкновений)(С.Аррениус и Я.Вант-Гофф; 1880-е г.г.):
1) Химическое взаимодействие между молекулами возможно только при их столкновении.
2) Не каждое столкновение молекул приводит к химическому взаимодействию, т. е. является результативным или, по терминологии Аррениуса, активным. Существует некий энергетический барьер, преодолеть который и вступить во взаимодействие может лишь часть молекул, причём, как правило, это очень малая часть от их общего числа в системе.
3) Причиной, обусловливающей существование энергетического барьера, является взаимное отталкивание электронных оболочек молекул при их сближении.
Когда две частицы удалены друг от друга на очень большое расстояние, между ними нет никакого взаимодействия и потенциальная энергия такой системы равна нулю. При меньших расстояниях между частицами они притягиваются друг к другу, и потенциальная энергия системы понижается. При дальнейшем уменьшении расстояния становятся заметными силы отталкивания электронных оболочек молекул и потенциальная энергия резко возрастает. Поэтому для сближения частиц до расстояния, на котором начнется перераспределение электронов на их орбиталях (т. е. химическое взаимодействие), частицы должны обладать достаточно большим запасом кинетической энергии. Силы отталкивания между частицами и представляют между собой так называемый потенциальный или энергетический барьер, а химическое взаимодействие возможно только в том случае, если сталкивающиеся молекулы способны преодолеть его.
4) Для того, чтобы молекулы могли при столкновении преодолеть энергетический барьер, они должны двигаться навстречу друг другу с достаточно большой скоростью. Для достижения этой необходимой скорости нужна определённая энергия, называемая энергией активации. Энергия активацииЕ* — это избыток энергии активных молекул по сравнению с неактивными, или иначе, энергия, которой должны обладать молекулы, чтобы иметь возможность вступить во взаимодействие. Размерность СИ энергии активации — Дж/моль.
5) Чем больше энергия активации реакции, тем больше энергетический барьер, и тем меньшее число молекул способно его преодолеть. Поэтому, чем больше Е*, тем медленнее идёт реакция.
6) С повышением температуры увеличивается скорость теплового движения молекул, поэтому доля активных молекул возрастает. Иными словами, при повышении температуры происходит термическая активация, приводящая к увеличению скорости реакции.
Возвращаясь к уравнению Аррениуса, отметим, что величина e — Е* / RT (“экспонента”) равна доле активных молекул, обладающих избыточной энергией Е* для вступления в химическое взаимодействие, а коэффициент А (предэкспоненциальный множитель) равен полной частоте соударений между молекулами реагирующих веществ в реакционном объёме.
Логарифмируя уравнение Аррениуса, получим уравнение прямой, не проходящей через начало координат:
| E* ln k = ln A — ¾¾ . RT |
Построив по экспериментальным данным график зависимости ln k от 1/T (т. н. “аррениусовскую зависимость”), можно вычислить энергию активации изучаемой реакции по тангенсу угла наклона, который в этом случае равен —Е*/R (рис. 12.5).
 Рис. 12.5. Аррениусовская зависимость и энергия активации Рис. 12.5. Аррениусовская зависимость и энергия активации |
Дифференцируя логарифмическую форму уравнения Аррениуса по температуре, получим уравнение, подобное уравнению изобары (изохоры) Вант-Гоффа:
| d ln k E* ¾¾¾ =¾¾ dT RT 2 |
Интегрирование его в пределах k1 ¸ k2 и Т1 ¸ Т2 приводит к уравнению
| k2 E* 1 1 ln ¾ = ¾ (¾ — ¾) k1 R T2 T1 |
| k2 E* Т2 — Т1 ln ¾ =¾ ( ¾¾¾) , (12.11) k1 R T1 T2 |
где k1 и k2 — константы скорости данной реакции при температурах T1 и T2 соответственно.
С помощью уравнения (12.11), также называемого уравнением Аррениуса, можно вычислить константу скорости k2 при заданной температуре Т2, если известны значения константы скорости k1 при температуре Т1 и энергия активации реакции Е*. Кроме того, это уравнение позволяет вычислить энергию активации реакции по значениям двух констант скорости при различных температурах:
| R T1 T2 k2 E* = ¾¾¾¾ ln¾ . Т2 — Т1 k1 |
Таким образом, в соответствии с теорией активных соударений повышение температуры увеличивает скорость химических реакций потому, что при этом возрастает доля активных молекул, способных преодолеть потенциальный барьер при столкновении.
Видео:Лекция 9: теория активных столкновений (06.11.2019)Скачать

Теория активных столкновений
Теория активных столкновений (С. Аррениус) основана на том, что химическое взаимодействие осуществляется только при столкновении активных частиц, которые обладают достаточной энергией для преодоления потенциального барьера реакции и ориентированы в пространстве друг относительно друга. Чтобы произошла реакция, частицы в момент столкновения должны обладать некоторым минимальным избытком энергии, называемым энергией активации.
В теории активных столкновений считается, что акт превращения начальных веществ в конечные продукты совершается в момент столкновения активных молекул и протекает мгновенно. При этом молекулы рассматриваются как бесструктурные частицы, хотя в действительности химические реакции происходят путем постепенной перестройки молекул и перераспределения энергии между химическими связями.
Согласно молекулярно-кинетической теории энергия активации равна разности между средней энергии активных столкновений и средней энергии всех столкновений. Доля активных молекул, как показывают расчеты, составляет примерно от 10 -20 до 10 -10 . Если эта доля меньше, то скорость реакции мала, если же она больше, то реакция происходит быстро, иногда практически мгновенно. Чем выше энергия активации данной реакции, тем при более высоких температурах она совершается. Энергия активации ниже энергии диссоциации реагирующих молекул, так как для протекания реакции достаточно такого ослабления связей в молекулах, при котором начинают преобладать силы образования новых связей.
Источники активации могут быть самые разнообразные. Реакции между ионами в растворе происходят с небольшой энергией активации, которая требуется для дегидратации ионов. Реакции между свободными атомами и радикалами не требуют энергии активации, так как атомы и радикалы являются активными частицами. В гомогенных газовых реакциях основным источником активации служат столкновения, доля которых определяется законом распределения Больцмана и растет с температурой. В гетерогенных каталитических реакциях источниками активации могут служить изменения, происходящие в реагирующих молекулах при адсорбции их поверхностью катализатора. Активация может быть вызвана также внешними причинами: поглощением квантов света при фотохимических реакциях, действием электрических разрядов, ударом электронов, α – частиц, нейтронов и других излучений.
При подсчете числа столкновений нужно учитывать эффективный диаметр молекул ?. Рассмотрим элементарную бимолекулярную реакцию:
А + В → Продукты (XI.1)
Предположим, что молекула А неподвижна, а молекулы В движутся в пространстве параллельно прямой, проходящей через центр молекулы А. При отсутствии взаимодействия между молекулами А и В с молекулой А столкнутся все молекулы В, центры которых находятся внутри цилиндра, имеющего радиус r.
где σ1 и σ2 – диаметры молекул А и В соответственно. При притяжении между молекулами А и В прямолинейные пути молекул В, начиная с некоторого расстояния, искривляются, и молекулы сближаются, в результате чего с молекулой А столкнется часть молекул В, центры которых первоначально находились вне цилиндра с радиусом r. Тогда
При отталкивании молекул
где σ’1, σ’2, σ»1, σ»2 – эффективные диаметры молекул. Таким образом, эффективный диаметр молекул характеризует не только диаметры сталкивающихся молекул, но и взаимодействие между ними. Величина πσ 2 12 называется сечением соударений и имеет большое значение в современной теории кинетики химических реакций.
Эффективный диаметр σ молекул одного вида в газе рассчитывается с помощью молекулярно-кинетической теории или по эмпирическим уравнениям. Средний эффективный диаметр при столкновении с молекул разного вида вычисляем по уравнению

Согласно молекулярно-кинетической теории газов полное число столкновений L0 за 1 с в 1 м 3 между одинаковыми молекулами рассчитываются по уравнению

где n – число молекул в 1 м 3 ; m – масса частиц, кг.
Если в системе реагируют молекулы двух разных видов, то

Число столкновений активных молекул La, рассчитанное на основе закона распределения Максвелла–Больцмана, определяется соотношением

где L0 – полное число столкновений; E’ – энергия активации.
Исходя из теории активных соударений и молекулярно-кинетических представлений, вычислим константу скорости элементарной бимолекулярной реакции (XI.1) с участием молекул двух видов. Скорость рассматриваемой элементарной реакции согласно основному постулату химической кинетики выражается уравнением
где k – константа скорости; c1 и c2 – концентрации веществ А и В, моль/м 3 ;


где n1 и n2 – число частиц А и В в 1 м 3 ; NA – число Авогадро.
Число активных столкновений равно числу реагирующих молекул А или В:

При этом скорость реакции

И с учетом (XI.8) и (XI.5) примет вид

Приравнивая правые части уравнений (XI.6) и (XI.10) с учетом (XI.7), получаем

Подставляя L0 из (XI.4) в (XI.11), получаем уравнение для расчета константы скорости реакции



Можно написать вместо (XI.13)
Подставляя (XI.15) в (XI.12), получаем:

Логарифмирование уравнения (XI.16) дает:

Дифференцирование по T равенства (XI.17) приводит к соотношению (так как В’ приближенно не зависит от температуры)

Прологарифмированное уравнение Аррениуса
где k – константа скорости реакции; A – предэкспоненциальный множитель; E – энергия активации. Продифференцируем его и сравним с (XI.18), то получим

При температуре 300 — 400 К RT/2 = 1,2 — 1,4 кДж/моль. Поскольку энергия активации химической реакции обычно имеет значение от 50 до 200 кДж/моль, то при практических расчетах можно считать Е ≈ Е’. Поэтому для приближенного расчета констант скоростей бимолекулярных реакций вместо Е’ можно использовать энергию активации Е, вычисленную по уравнению Аррениуса на основании опытных данных.
Уравнение (XI.12) можно рассматривать как теоретическое обоснование уравнения Аррениуса на основе теории активных столкновений. Энергия активации в теории активных столкновений не вычисляется, а определяется опытным путем по зависимости скорости реакции от температуры. (Для некоторых сравнительно простых элементарных реакций энергия активации может быть вычислена из квантово-химических представлений). Предэкспоненциальные множители для бимолекулярных элементарных реакций рассчитываются по уравнению (XI.13). Однако бимолекулярные реакции, для которых экспериментально найденные предэкспоненциальные множители совпадают с рассчитанными, встречаются сравнительно редко. Чаще всего предэкспоненциальные множители, рассчитанные теоретически как для реакций в газах, так и растворах, значительно превышают экспериментальные значения. Это связано с упрощенным характером теории активных столкновений, которая считает, что столкновения между молекулами аналогичны столкновениям упругих шаров. В связи с этим в уравнение (XI.12) вводится множитель P, учитывающий отклонение теоретических расчетов от опытных данных. Этот множитель называется стерическим или энтропийным фактором. Уравнение (XI.12) с учетом этого фактора принимает вид

При столкновении активных молекул должно быть вполне определенное расположение в пространстве активных групп, входящих в состав молекулы, которое бы обеспечило образование конечных продуктов. Стерический фактор P в большинстве случаев характеризует вероятность определенной геометрической конфигурации частиц при столкновении.
Есть и другие причины, приводящие к расхождению теории активных столкновений с опытом, которые также учитываются стерическим или энтропийным фактором. Вследствие туннельного эффекта элементарный акт может произойти при значениях энергии активации меньше Е. Это формально характеризуется величиной Р > 1. Вновь образующиеся молекулы могут быть сильно возбужденными. Если такие молекулы не освободятся от избытка энергии после своего возникновения, то они вновь могут превратиться в молекулы исходного вещества; в этом случае Р > k2

где k1 = cAB / (cA cB) – константа равновесия. Вторая стадия реакции является лимитирующей.
Во втором предельном случае при k-1 3 раствора; dc2 / dr – градиент концентрации вещества B.
Чтобы определить поток J , разделим переменные r и c2 и проинтегрируем (XI.96) от R * до ∞ и от 0 до c2:

где R * – расстояние между молекулами A и B при образовании пары столкновения; полагаем, что на расстоянии меньше R, c2 = 0.
Для простоты полагаем, что раствор достаточно разбавленный, и в процессе диффузии молекул B к молекуле A через слой раствора они не встречаются с другими молекулами, A и, поэтому, поток J имеет постоянное значение.
В результате интегрирования (XI.97), получаем
Скорость реакции, контролируемая диффузией, определяется скоростью потока молекул B к молекуле A. При этом скорость реакции w равна числу пар столкновения, которые образуются в 1 с в 1 м 3 раствора:

где n1 = NA c1 – число молекул A в 1 м 3 раствора.
Подставляя значение J из (XI.98) в (XI.99), определяем
где D = D1 + D2, так как нужно учесть, что молекулы A также диффундируют в растворе навстречу молекулам B.
Приравнивая правые части уравнений (XI.100) и (XI.92), получаем для k3 выражение
Это выражение можно преобразовать, если для D1 и D2 использовать соотношение Стокса–Эйнштейна



где η – коэффициент вязкости раствора (или растворителя для достаточно разбавленного раствора). Подставляя (XI.103) в (XI.101), получаем


Таким образом, в рассмотренном предельном случае ( k1 ≠ → Продукты (XI.105)
константа скорости согласно (*) (при χ = 1) равна

Но термодинамическая константа равновесия в растворе выражается через активности


Подставляя уравнение (XI.108) в (XI.106), получаем

При γA = γB = γ ≠ = 1 уравнение (XI.109) преобразуется к виду
где k0 – константа скорости реакции, коэффициенты активности равны единице. Между константами k и k0 имеется соотношение

С этим случаем мы встречаемся, например, когда одна и та же реакция может проводиться как в газовой фазе ( k0 ), так и в растворе ( k ).
Если исходные вещества A и B являются молекулами и, кроме того, принять γA = γB = γ ≠ = γ, то из выражения (XI.110) получаем, что k = k0 γ. Это означает, что для бимолекулярных реакций между молекулами константы скорости реакции при проведении ее в газовой фазе и в растворе различны.
Для мономолекулярной реакции
А → А ≠ → Продукты (XI.111)
Рассуждая аналогично, получаем выражение

Если вещество A находится в растворе в молекулярной форме и принимая γA = γ ≠ = γ, то из уравнения (XI.112) получаем, что k = k0, т.е. для мономолекулярной реакции теория абсолютных скоростей реакций предсказывает слабое влияние растворителя и его природы на кинетику реакции, если конфигурация активированного комплекса мало отличается от исходных молекул.
Опыт во многих случаях подтверждает теорию. Например, мономолекулярная реакция разложения оксида азота ( N2O5 ) в газовой фазе при температуре 293 К имеет константу скорости, равную 3,4 ⋅ 10 -5 с -1 . При использовании в качестве растворителя хлороформа, дихлорэтана, нитрометана, жидкого брома и тетрахлорида углерода константы скорости при той же температуре равны соответственно 3,7 ⋅ 10 -5 ; 4,2 ⋅ 10 -5 ; 3,1 ⋅ 10 -5 ; 4,1 ⋅ 10 -5 с -1 . В случае бимолекулярных элементарных реакций перенос реакции из газовой фазы в раствор, а также изменение природы растворителя, как правило, заметно влияют на константу скорости реакции в соответствии с предсказанием теории абсолютных скоростей реакций.
Важное подтверждение теории абсолютных скоростей реакций получила для реакций между ионами в растворах сильных электролитов, так как в этом случае коэффициенты активности могут быть вычислены из теории сильных электролитов Дебая–Хюккеля. Если раствор электролита разбавленный, то коэффициенты активности можно выразить приближенно с помощью предельного закона Дебая–Хюккеля:

где A – теоретический коэффициент, который для водных растворов равен 0,509; zi – заряд i-го иона; I – ионная сила раствора.
Если в реакции (XI.105) исходные вещества A и B являются ионами с зарядами zA и zB , то коэффициенты активности в уравнении (XI.110) можно приближенно выразить из уравнения (XI.113), принимая, что заряд активированного комплекса равен алгебраической сумме zA + zB зарядов реагирующих ионов:

Таким образом, из теории активированного комплекса следует, что если в бимолекулярной реакции в растворе участвуют два иона с одинаковыми зарядами ( zA zB > 0 ), то lg ( k / k0 ) > 0 и константа скорости реакции увеличивается с ростом ионной силы раствора. Если же заряды ионов противоположные ( zA zB < 0 ), то и константа скорости реакции уменьшается с ростом ионной силы. Кроме того, согласно уравнению (XI.114) график в координатах lg ( k / k0 ) — √I в достаточно разбавленных растворах должен изображаться прямыми линиями, выходящими из начала координат, причем чем больше произведение zA zB, тем больше должен быть угол наклона этих прямых. Опытные данные хорошо подтверждают предсказания теории (рис.2).
Влияние ионной силы раствора на константу скорости реакции между ионами из-за изменения коэффициента активности ионов в растворах сильных электролитов называется первичным (или кинетическим) солевым эффектом. В реакциях с участием одного из ионов слабого электролита (например, иона водорода слабой кислоты) посторонний электролиз может влиять непосредственно на его концентрацию и, следовательно, на скорость реакции. Это – вторичный солевой эффект.
Видео:Использование уравнения Аррениуса для решения задач (1/2). Химия для поступающих.Скачать

ХИМИЧЕСКАЯ КИНЕТИКА
ХИМИЧЕСКАЯ КИНЕТИКА – (от греч. кинетикос – движущий) наука о механизмах химических реакций и закономерностях их протекания во времени.
В 19 в. результате развития основ химической термодинамики химики научились рассчитывать состав равновесной смеси для обратимых химических реакций. Кроме того, на основании несложных расчетов можно было, не проводя экспериментов, сделать вывод о принципиальной возможности или невозможности протекания конкретной реакции в данных условиях. Однако «принципиальная возможность» реакции еще не означает, что она пойдет. Например, реакция С + О2 → СО2 с точки зрения термодинамики весьма благоприятна, во всяком случае, при температурах ниже 1000° С (при более высоких температурах происходит уже распад молекул СО2), т.е. углерод и кислород должны (практически со 100%-ным выходом) превратиться в диоксид углерода. Однако опыт показывает, что кусок угля может годами лежать на воздухе, при свободном доступе кислорода, не претерпевая никаких изменений. То же можно сказать и о множестве других известных реакций. Например, смеси водорода с хлором или с кислородом могут сохраняться очень долго без всяких признаков химических реакций, хотя в обоих случаях реакции термодинамически благоприятны. Это означает, что после достижения равновесия в стехиометрической смеси H2 + Cl2 должен остаться только хлороводород, а в смеси 2Н2 + О2 – только вода. Другой пример: газообразный ацетилен вполне стабилен, хотя реакция C2H2 → 2C + H2 не только термодинамически разрешена, но и сопровождается значительным выделением энергии. Действительно, при высоких давлениях, ацетилен взрывается, однако в обычных условиях он вполне стабилен.
Термодинамически разрешенные реакции, подобные рассмотренным, могут пойти только в определенных условиях. Например, после поджигания уголь или сера самопроизвольно соединяются с кислородом; водород легко реагирует с хлором при повышении температуры или при действии ультрафиолетового света; смесь водорода с кислородом (гремучий газ) взрывается при поджигании или при внесении катализатора. Почему же для осуществления всех этих реакций необходимы специальные воздействия – нагревание, облучение, действие катализаторов? Химическая термодинамика не дает ответа на этот вопрос – понятие времени в ней отсутствует. В то же время для практических целей очень важно знать, пройдет ли данная реакция за секунду, за год или же за многие тысячелетия.
Опыт показывает, что скорость разных реакций может отличаться очень сильно. Практически мгновенно идут многие реакции в водных растворах. Так, при добавлении избытка кислоты к щелочному раствору фенолфталеина малинового цвета раствор мгновенно обесцвечивается, это означает, что реакция нейтрализации, а также реакция превращения окрашенной формы индикатора в бесцветную идут очень быстро. Значительно медленнее идет реакция окисления водного раствора иодида калия кислородом воздуха: желтая окраска продукта реакции – иода появляется лишь через продолжительное время. Медленно протекают процессы коррозии железных и особенно медных сплавов, многие другие процессы.
Предсказание скорости химической реакции, а также выяснение зависимости этой скорости от условий проведения реакции – одна из важных задач химической кинетики – науки, изучающей закономерности протекания реакций во времени. Не менее важна и вторая задача, стоящая перед химической кинетикой – изучение механизма химических реакций, то есть детального пути превращения исходных веществ в продукты реакции.
Видео:Как температура влияет на скорость химической реакции? Уравнение АррениусаСкачать

Скорость реакции.
Проще всего определить скорость для реакции, протекающей между газообразными или жидкими реагентами в гомогенной (однородной) смеси в сосуде постоянного объема. В этом случае скорость реакции определяется как изменение концентрации любого из участвующих в реакции веществ (это может быть исходное вещество или продукт реакции) в единицу времени. Это определение можно записать в виде производной: v = dc/dt, где v – скорость реакции; t – временя, c – концентрация. Эту скорость легко определить, если есть экспериментальные данные по зависимости концентрации вещества от времени. По этим данным можно построить график, который называется кинетической кривой. Скорость реакции в заданной точке кинетической кривой определяется наклоном касательной в этой точке. Определение наклона касательной всегда связано с некоторой ошибкой. Точнее всего определяется начальная скорость реакции, поскольку вначале кинетическая кривая обычно близка к прямой; это облегчает проведение касательной в начальной точке кривой.
Если время измерять в секундах, а концентрацию – в молях на литр, то скорость реакции измеряется в единицах моль/(л·с). Таким образом, скорость реакции не зависит от объема реакционной смеси: при одинаковых условиях она будет одинаковой и в маленькой пробирке, и в многотоннажном реакторе.
Величина dt всегда положительна, тогда как знак dc зависит от того, как изменяется со временем концентрация – уменьшается (для исходных веществ) или увеличивается (для продуктов реакции). Чтобы скорость реакции всегда оставалась величиной положительной, в случае исходных веществ перед производной ставят знак минус: v = –dc/dt. Если реакция идет в газовой фазе, вместо концентрации веществ в уравнении скорости часто используют давление. Если газ близок к идеальному, то давление р связано с концентрацией с простым уравнением: p = cRT.
В ходе реакции разные вещества могут расходоваться и образовываться с разной скоростью, в соответствии с коэффициентами в стехиометрическом уравнении (см. СТЕХИОМЕТРИЯ), поэтому, определяя скорость конкретной реакции, следует учитывать эти коэффициенты. Например, в реакции синтеза аммиака 3H2 + N2 → 2NH3 водород расходуется в 3 раза быстрее, чем азот, а аммиак накапливается в 2 раза быстрее, чем расходуется азот. Пэтому уравнение скорости для этой реакции записывают следующим образом: v = –1/3 dp(H2)/dt = –dp(N2)/dt = +1/2 dp(NH3)/dt. В общем случае, если реакция стехиометрическая, т.е. протекает точно в соответствии с записанным уравнением: aA + bB → cC + dD, ее скорость определяют как v = –(1/a)d[A]/dt = –(1/b)d[B]/dt = (1/c)d[C]/dt = (1/d)d[D]/dt (квадратными скобками принято указывать молярную концентрацию веществ). Таким образом, скорости по каждому веществу жестко связаны между собой и, определив экспериментально скорость для любого участника реакции, легко рассчитать ее для любого другого вещества.
Большинство реакций, используемых в промышленности, относятся к гетерогенно-каталитическим. Они протекают на поверхности раздела фаз между твердым катализатором и газовой или жидкой фазой. На поверхности раздела двух фаз протекают и такие реакции как обжиг сульфидов, растворение металлов, оксидов и карбонатов в кислотах, ряд других процессов. Для таких реакций скорость зависит и от величины поверхности раздела, поэтому скорость гетерогенной реакции относят не к единице объема, а к единице поверхности. Измерить величину поверхности, на которой идет реакция, не всегда просто.
Если реакция протекает в замкнутом объеме, то ее скорость в большинстве случаев максимальна в начальный момент времени (когда максимальна концентрация исходных веществ), а затем, по мере превращения исходных реагентов в продукты и, соответственно, снижения их концентрации, скорость реакции уменьшается. Встречаются и реакции, в которых скорость увеличивается со временем. Например, если медную пластинку опустить в раствор чистой азотной кислоты, то скорость реакции будет расти со временем, что легко наблюдать визуально. Ускоряются со временем также процессы растворения алюминия в растворах щелочей, окисления многих органических соединений кислородом, ряд других процессов. Причины такого ускорения могут быть разными. Например, это может быть связано с удалением защитной оксидной пленки с поверхности металла, или с постепенным разогревом реакционной смеси, или с накоплением веществ, ускоряющих реакцию (такие реакции называются автокаталитическими).
В промышленности реакции обычно проводят путем непрерывной подачи в реактор исходных веществ и вывода продуктов. В таких условиях можно добиться постоянной скорости протекания химической реакции. С постоянной скоростью протекают и фотохимические реакции при условии полного поглощения падающего света (см. ФОТОХИМИЧЕСКИЕ РЕАКЦИИ).
Видео:Уравнение Аррениуса, часть 1Скачать

Лимитирующая стадия реакции.
Если реакция осуществляется путем последовательно протекающих стадий (не обязательно все из них являются химическими) и одна из этих стадий требует значительно большего времени, чем остальные, то есть идет намного медленнее, то такая стадия называется лимитирующей. Именно эта самая медленная стадия определяет скорость всего процесса. Рассмотрим в качестве примера каталитическую реакцию окисления аммиака. Здесь возможны два предельных случая.
1. Поступление молекул реагентов – аммиака и кислорода к поверхности катализатора (физический процесс) происходит значительно медленнее, чем сама каталитическая реакция на поверхности. Тогда для повышения скорости образования целевого продукта – оксида азота совершенно бесполезно повышать эффективность катализатора, а надо позаботиться об ускорении доступа реагентов к поверхности.
2. Подача реагентов к поверхности происходит значительно быстрее самой химической реакции. Вот здесь имеет смысл совершенствовать катализатор, подбирать оптимальные условия для каталитической реакции, так как лимитирующей стадией в данном случае является каталитическая реакция на поверхности.
Видео:Влияние температуры на скорость химических реакций. 10 класс.Скачать

Теория столкновений.
Исторически первой теорией, на основании которой можно было рассчитывать скорости химических реакций, была теория столкновений. Очевидно, что для того, чтобы молекулы прореагировали, они прежде всего должны столкнуться. Отсюда следует, что реакция должна идти тем быстрее, чем чаще сталкиваются друг с другом молекулы исходных веществ. Поэтому каждый фактор, влияющий на частоту столкновений между молекулами, будет влиять и на скорость реакции. Некоторые важные закономерности, касающиеся столкновений между молекулами, были получены на основании молекулярно-кинетической теории газов.
В газовой фазе молекулы движутся с большими скоростями (сотни метров в секунду) и очень часто сталкиваются друг с другом. Частота столкновений определяется прежде всего числом частиц в единице объема, то есть концентрацией (давлением). Частота столкновений зависит также и от температуры (с ее повышением молекулы движутся быстрее) и от размера молекул (большие молекулы сталкиваются друг с другом чаще, чем маленькие). Однако концентрация влияет на частоту столкновений значительно сильнее. При комнатной температуре и атмосферном давлении каждая молекула средних размеров испытывает в секунду несколько миллиардов столкновений.
На основании этих данных можно рассчитать скорость реакции А + В → С между двумя газообразными соединениями А и В, предполагая, что химическая реакция проходит при каждом столкновении молекул реагентов. Пусть в литровой колбе при атмосферном давлении есть смесь реагентов А и В при равных концентрациях. Всего в колбе будет 6·10 23 /22,4 = 2,7·10 22 молекул, из которых 1,35·10 22 молекул вещества А и столько же молекул вещества В. Пусть за 1 с каждая молекула А испытывает 10 9 столкновений с другими молекулами, из которых половина (5·10 8 ) приходится на столкновения с молекулами В (столкновения А + А не приводят к реакции). Тогда всего в колбе за 1 с происходит 1,35·10 22 ·5·10 8
7·10 30 столкновений молекул А и В. Очевидно, что если бы каждое из них приводило к реакции, она прошла бы мгновенно. Однако многие реакции идут достаточно медленно. Отсюда можно сделать вывод, что лишь ничтожная доля столкновений между молекулами реагентов приводит к взаимодействию между ними.
Для создания теории, которая позволяла бы рассчитать скорость реакции на основании молекулярно-кинетической теории газов, нужно было уметь рассчитывать общее число столкновений молекул и долю «активных» столкновений, приводящих реакции. Нужно было также объяснить, почему скорость большинства химических реакций сильно возрастает при повышении температуры – скорость молекул и частота столкновений между ними увеличиваются с температурой незначительно – пропорционально 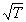
Эти проблемы были решены на основании теории столкновений следующим образом. При столкновениях молекулы непрерывно обмениваются скоростями и энергиями. Так, данная молекула в результате «удачного» столкновения может заметно увеличить свою скорость, тогда как при «неудачном» столкновении она может почти остановиться (похожую ситуацию можно наблюдать на примере бильярдных шаров). При нормальном атмосферном давлении столкновения, а следовательно, изменения скорости происходят с каждой молекулой миллиарды раз в секунду. При этом скорости и энергии молекул в значительной степени усредняются. Если в данный момент времени «пересчитать» в заданном объеме газа молекулы, обладающие определенными скоростями, то окажется, что значительная часть их имеет скорость, близкую к средней. В то же время многие молекулы обладают скоростью меньше средней, а часть движется со скоростями больше средней. С увеличением скорости доля молекул, имеющих данную скорость, быстро уменьшается. В соответствии с теорией столкновений, реагируют только те молекулы, которые при столкновении обладают достаточно высокой скоростью (и, следовательно, большим запасом кинетической энергии). Такое предположение было сделано в 1889 году шведским химиком Сванте Аррениусом.
Видео:Теории кислот, оснований и растворов. Теория Аррениуса-Оствальда. 11 класс.Скачать

Энергия активации.
Аррениус ввел в обиход химиков очень важное понятие энергии активации (Ea) – это та минимальная энергия, которой должна обладать молекула (или пара реагирующих молекул), чтобы вступить в химическую реакцию. Энергию активации измеряют обычно в джоулях и относят не к одной молекуле (это очень маленькая величина), а к молю вещества и выражают в единицах Дж/моль или кДж/моль. Если энергия сталкивающихся молекул меньше энергии активации, то реакция не пойдет, а если равна или больше, то молекулы прореагируют.
Энергии активации для разных реакций определяют экспериментально (из зависимости скорости реакции от температуры). Изменяться энергия активации может в довольно широких пределах – от единиц до нескольких сотен кДж/моль. Например, для реакции 2NO2 → N2O4 энергия активации близка к нулю, для реакции 2Н2О2 → 2Н2О + О2 в водных растворах Ea = 73 кДж/моль, для термического разложения этана на этилен и водород Ea = 306 кДж/моль.
Энергия активации большинства химических реакций значительно превышает среднюю кинетическую энергию молекул, которая при комнатной температуре составляет всего лишь около 4 кДж/моль и даже при температуре 1000° С не превышает 16 кДж/моль. Таким образом, чтобы прореагировать, молекулы обычно должны иметь скорость значительно больше средней. Например, в случае Ea = 200 кДж/моль сталкивающиеся молекулы небольшой молекулярной массы должны иметь скорость порядка 2,5 км/с (энергия активации в 25 раз больше средней энергии молекул при 20° С). И это – общее правило: для большинства химических реакций энергия активации значительно превышает среднюю кинетическую энергию молекул.
Вероятность для молекулы запасти в результате серии столкновений большую энергию очень мала: такой процесс требует для нее колоссального числа последовательных «удачных» столкновений, в результате которых молекула только набирает энергию, не теряя ее. Поэтому для многих реакций лишь ничтожная доля молекул имеет энергию, достаточную для преодоления барьера. Эта доля, в соответствии с теорией Аррениуса, определяется формулой: a = e –Ea /RT = 10 –Ea /2,3RT
10 –Ea /19Т, где R = 8,31 Дж/(моль . К). Из формулы следует, что доля молекул, обладающих энергией Ea, как и доля активных столкновений a, очень сильно зависит как от энергии активации, так и от температуры. Например, для реакции с Ea = 200 кДж/моль при комнатной температуре (Т
300 К) доля активных столкновений ничтожно мала: a = 10 –200000/(19,300)
10 –35 . И если каждую секунду в сосуде происходит 7·10 30 столкновений молекул А и В, то понятно, что реакция идти не будет.
Если увеличить вдвое абсолютную температуру, т.е. нагреть смесь до 600 К (327° С); при этом доля активных столкновений резко возрастет: a = 10 –200000/(19,600)
4·10 –18 . Таким образом, повышение температуры в 2 раза увеличило долю активных столкновений в 4·10 17 раз. Теперь каждую секунду из общего числа примерно 7·10 30 столкновений к реакции будет приводить 7·10 30 ·4·10 –18
3·10 13 . Такая реакция, в которой каждую секунду исчезает 3·10 13 молекул (из примерно 10 22 ), хотя и очень медленно, но все же идет. Наконец, при температуре 1000 К (727° C) a
3·10 –11 (из каждых 30 миллиардов столкновений данной молекулы реагента одно приводит к реакции). Это уже много, так как за 1 с в реакцию будут вступать 7·10 30 ·3·10 –11 = 2·10 20 молекул, и такая реакция пройдет за несколько минут (с учетом снижения частоты столкновений с уменьшением концентрации реагентов).
Теперь понятно, почему повышение температуры может так сильно увеличить скорость реакции. Средняя скорость (и энергия) молекул с повышением температуры увеличивается незначительно, но зато резко повышается доля «быстрых» (или «активных») молекул, обладающих достаточной для протекания реакции скоростью движения или достаточной колебательной энергией.
Расчет скорости реакции с учетом общего числа столкновений и доли активных молекул (т.е. энергии активации), часто дает удовлетворительное соответствие с экспериментальными данными. Однако для многих реакций наблюдаемая на опыте скорость оказывается меньше рассчитанной по теории столкновений. Это объясняется тем, что для осуществления реакции нужно, чтобы столкновение было удачным не только энергетически, но и «геометрически», то есть молекулы должны в момент столкновения определенным образом ориентироваться относительно друг друга. Таким образом, при расчетах скорости реакций по теории столкновений, помимо энергетического, учитывают и стерический (пространственный) фактор для данной реакции.
Видео:Коробов М. В. - Физическая химия II - Теория активных столкновений: основное уравнениеСкачать

Уравнение Аррениуса.
Зависимость скорости реакции от температуры обычно описывают уравнением Аррениуса, которое в простейшем виде можно записать как v = v0 a = v0e –Ea/RT , где v0 – скорость, которую имела бы реакция при нулевой энергии активации (фактически это частота столкновений в единице объеме). Поскольку v0 слабо зависит от температуры, все определяет второй сомножитель – экспоненциальный: с увеличением температуры этот сомножитель быстро увеличивается, причем тем быстрее, чем больше энергия активации Еа. Указанная зависимость скорости реакции от температуры называется уравнением Аррениуса, оно – одно из важнейших в химической кинетике. Для приблизительной оценки влияния температуры на скорость реакции иногда используют так называемое «правило Вант-Гоффа» (см. ВАНТ-ГОФФА ПРАВИЛО).
Если реакция подчиняется уравнению Аррениуса, логарифм ее скорости (измеренной, например, в начальный момент) должен линейно зависеть от абсолютной температуры, то есть график зависимости lnv от 1/Т должен быть прямолинейным. Наклон этой прямой равен энергии активации реакции. По такому графику можно предсказать, какова будет скорость реакции при данной температуре или же – при какой температуре реакция будет идти с заданной скоростью.
Несколько практических примеров использования уравнения Аррениуса.
1. На упаковке замороженного продукта написано, что его можно хранить на полке холодильника (5° С) в течение суток, в морозильнике, отмеченном одной звездочкой (–6° С), – неделю, двумя звездочками (–12° С) – месяц, а в морозильнике со значком *** (что означает температуру в нем –18° С) – 3 месяца. Предположив, что скорость порчи продукта обратно пропорциональна гарантийному сроку хранения tхр, в координатах lntхр, 1/Т получаем, в соответствии с уравнением Аррениуса, прямую. Из нее можно рассчитать энергию активации биохимических реакций, приводящие к порче данного продукта (около 115 кДж/моль). Из того же графика можно выяснить, до какой температуры надо охладить продукт, чтобы его можно было хранить, например, 3 года; получается –29° С.
2. Альпинисты знают, что в горах трудно сварить яйцо, и вообще любую пищу, требующую более или менее длительного кипячения. Качественно причина этого понятна: с понижением атмосферного давления уменьшается температура кипения воды. С помощью уравнения Аррениуса можно рассчитать, сколько времени потребуется, например, чтобы сварить вкрутую яйцо в г. Мехико, расположенном на высоте 2265 м, где нормальным считается давление 580 мм рт.ст., а вода при таком пониженном давлении кипит при 93° С. Энергия активации реакция «свертывания» (денатурации) белка была измерена и оказалась очень большой по сравнению со многими другими химическими реакциями – порядка 400 кДж/моль (она может несколько отличаться для различных белков). В таком случае понижение температуры от 100 до 93° С (то есть от 373 до 366 К) приведет к замедлению реакции в 10 (400000/19)(1/366 – 1/373) = 11,8 раза. Именно поэтому жители высокогорья предпочитают варке пищи ее жарку: температура сковородки, в отличие от температуры кастрюли с кипятком, не зависит от атмосферного давления.
3. В кастрюле-скороварке пища готовится при повышенном давлении и, следовательно, при повышенной температуре кипения воды. Известно, что в обычной кастрюле говядина варится 2–3 часа, а компот из яблок – 10–15 мин. Учитывая, что оба процесса имеют близкую энергию активации (около 120 кДж/моль), можно по уравнению Аррениуса рассчитать, что в скороварке при 118°С мясо будет вариться 25–30 мин, а компот – всего 2 мин.
Уравнение Аррениуса очень важно для химической промышленности. При протекании экзотермической реакции выделяющаяся тепловая энергия нагревает не только окружающую среду, но и сами реагенты. это может привести к нежелательному сильному ускорению реакции. Расчет изменения скорости реакции и скорости тепловыделения при повышении температуры позволяет избежать теплового взрыва (см. ВЗРЫВЧАТЫЕ ВЕЩЕСТВА).
Видео:С.Аррениус. Определение кислоты как вещества (видео 1) | Кислоты и Основания | ХимияСкачать

Зависимость скорости реакции от концентрации реагентов.
Скорость большинства реакций со временем постепенно снижается. Этот результат хорошо согласуется с теорией столкновений: по мере протекания реакции концентрации исходных веществ падают, снижается и частота столкновений между ними; соответственно уменьшается и частота столкновения активных молекул. Это приводит к уменьшению скорости реакции. В этом состоит сущность одного из основных законов химической кинетики: скорость химической реакции пропорциональна концентрации реагирующих молекул. Математически это можно записать в виде формулы v = k[A][B], где k – постоянная, называемая константой скорости реакции. Приведенное уравнение называется уравнением скорости химической реакции или кинетическим уравнением. Константа скорости для данной реакции не зависит от концентрации реагентов и от времени, но она зависит от температуры в соответствии с уравнением Аррениуса: k = k0e –Ea/RT .
Простейшее уравнение скорости v = k[A][B] всегда справедливо в том случае, когда молекулы (или другие частицы, например, ионы) А, сталкиваясь с молекулами В, могут непосредственно превращаться в продукты реакции. Подобные реакции, идущие в один прием (как говорят химики, в одну стадию), называются элементарными реакциями. Таких реакций немного. Большинство реакций (даже таких с виду таких простых как H2 + I2 ® 2HI) не являются элементарными, поэтому исходя из стехиометрического уравнения такой реакции записать его кинетическое уравнение нельзя.
Кинетическое уравнение можно получить двумя способами: экспериментально – измеряя зависимость скорости реакции от концентрации каждого реагента по отдельности, и теоретически – если известен детальный механизм реакции. Чаще всего (но не всегда) кинетическое уравнение имеет вид v = k[A] x [B] y , где x и y называются порядками реакции по реагентам А и В. Эти порядки, в общем случае, могут быть целыми и дробными, положительными и даже отрицательными. Например, кинетическое уравнение для реакции термического распада ацетальдегида CH3CHO ® CH4 + CO имеет вид v = k[CH3CHO] 1,5 , т.е. реакция имеет полуторный порядок. Иногда возможно случайное совпадение стехиометрических коэффициентов и порядков реакции. Так, эксперимент показывает, что реакция H2 + I2 ® 2HI имеет первый порядок как по водороду, так и по иоду, то есть ее кинетическое уравнение имеет вид v = k[H2][I2] (именно поэтому эту реакцию в течение многих десятилетий считали элементарной, пока в 1967 не был доказан ее более сложный механизм).
Если известно кинетическое уравнение, т.е. известно, как скорость реакции зависит от концентраций реагентов в каждый момент времени, и известна константа скорости, то можно рассчитать зависимость от времени концентраций реагентов и продуктов реакции, т.е. теоретически получить все кинетические кривые. Для таких расчетов используются методы высшей математики или компьютерные расчеты, и они не представляют принципиальных трудностей.
С другой стороны, полученное экспериментально кинетическое уравнение помогает судить о механизме реакции, т.е. о совокупности простых (элементарных) реакций. Выяснение механизмов реакций является важнейшей задачей химической кинетики. Это очень трудная задача, так как механизм даже простой с виду реакции может включать множество элементарных стадий.
Можно проиллюстрировать применение кинетических методов для определения механизма реакции на примере щелочного гидролиза алкилгалогенидов с образованием спиртов: RX + OH – → ROH + X – . Экспериментально было обнаружено, что для R = CH3, C2H5 и т.д. и X = Cl скорость реакции прямо пропорционально концентрациям реагентов, т.е. имеет первый порядок по галогениду RX и первый – по щелочи, и кинетическое уравнение имеет вид v = k1[RX][OH – ]. В случае третичных алкилиодидов (R = (CH3)3C, X = I) порядок по RX – первый, а по щелочи – нулевой: v = k2[RX]. В промежуточных случаях, например, для изопропилбромида (R = (CH3)2CH, X = Br), реакция описывается более сложным кинетическим уравнением: v = k1[RX][OH – ] + k2[RX]. На основании этих кинетических данных был сделан следующий вывод о механизмах подобных реакций.
В первом случае реакция идет в один прием, путем непосредственного столкновения молекул спирта с ионами ОН – (так называемый механизм SN2). Во втором случае реакция идет в две стадии. Первая стадия – медленная диссоциация алкилиодида на два иона: RI → R + + I – . Вторая – очень быстрая реакция между ионами: R + + OH – → ROH. Скорость суммарной реакции зависит только от медленной (лимитирующей) стадии, поэтому она не зависит от концентрации щелочи; отсюда – нулевой порядок по щелочи (механизм SN1). В случае вторичных алкилбромидов осуществляются одновременно оба механизма, поэтому кинетическое уравнение более сложное.
🔍 Видео
ДВИ по химии. Термохимия. Уравнение Аррениуса, закон Гесса, задачи на теплоемкостьСкачать

Порядок реакции и энергия активацииСкачать

Лекция 8: уравнение Аррениуса (30.10.2019)Скачать

Решение задач на тему: "Правило Вант-Гоффа". 1 часть. 10 класс.Скачать

Кинетика || Лекция 16 || Теория активных столкновенийСкачать

6 Уравнение Аррениуса, ч 2Скачать

Лекция 10: теория активных столкновений, схема Линдемана (13.11.2019)Скачать

Лекция 14 || 2021 || Статистический смысл энергии активации, теория активных столкновенийСкачать

Лекция 13 || 2021 || Температурная зависимость скорости, уравнение Аррениуса, энергия активацииСкачать
Использование уравнения Аррениуса для решения задач (2/2). Химия для поступающих.Скачать

Вахрушева В А Скорость химической реакцииСкачать

Лекция 25.11.20 | Статистический смысл энергии активации, Теория столкновений | Химическая кинетикаСкачать