Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Муниципальное бюджетное общеобразовательное учреждение
Семлевская средняя общеобразовательная школа №1
Вяземского района Смоленской области
Научно-исследовательская работа по теме
«Теория сравнения по модулю»
Подготовила
ученица 9 класса: Попова Анастасия
Преподаватель: Перцева С.М.
Понятие модуля числа известно каждому, а вот что означает понятие сравнение по модулю, знают далеко не все. Тема моей работы «Теория сравнения по модулю». Я обратилась к этой теме, так как она недостаточно полно изложена в действующих учебниках математики, а задачи по этой теме предлагаются как на олимпиадах, так и на вступительных экзаменах в вузы.
Цель работы : разобраться с понятием «сравнение по модулю», развить умение применять знания в решении практических заданий .
1) Изучить краткий исторический обзор возникновения теории;
2) Дать определение сравнения по модулю;
3) Изучить свойства сравнения по модулю;
4) Рассмотреть операции со сравнениями;
5) Применить знания для решения практических заданий.
1)Теоретический анализ и обобщение научной литературы;
2)Математический расчет;
1.Историческая справка . Предпосылкой к созданию теории сравнений стало восстановление сочинений Диофанта, которые были выпущены в подлиннике и с латинским переводом, благодаря Баше де Мезириаку, в 1621. Их изучение привело Ферма́ к открытиям, которые по значению существенно опередили свое время. Этой же темой независимо от Ферма занимался Лейбниц. Позже изучение вопросов теории сравнений, было продолжено Эйлером. Утвердившуюся в математике символику предложил Гаусс. Он же впервые использовал сравнения по модулю в своей книге «Арифметические исследования» в 1801 году. Гаусс преобразовал все накопленные до него сведения, связанные с операциями сравнения по модулю, в стройную теорию, которая и была впервые изложена в этой книге.
Теорию сравнения по модулю называют модульной арифметикой. В математике модульная арифметика — система арифметики для целых чисел, где числа «обертывают вокруг» после достижения определенной стоимости — модуль . Знакомое использование модульной арифметики находится в 12-часовых часах , в которых день разделен на два 12-часовых периода. Если время будет 7:00 теперь, то 8 часов спустя это будет 3:00. Обычное дополнение предложило бы, чтобы более позднее время было 7 + 8 = 15, но это не ответ, потому что время часов «обертывает вокруг» каждые 12 часов; в 12-часовое время нет никаких «15 часов». Аналогично, если запуски часов в 12:00 (полдень) и 21 час протекут, то время будет 9:00 на следующий день, а не 33:00. Так как число часа начинается после того, как оно достигает 12, это — арифметический модуль 12. Согласно определению ниже, 12 подходящее не только 12 самому, но также и 0, таким образом, время, названное «12:00», можно было также назвать «0:00», так как 12 подходящее 0 модулям 12.
Если два целых числа 
и 
при делении на 
дают одинаковые остатки, то они называются сравнимыми по модулю числа .
Сравнимость чисел и записывается в виде формулы ( сравнения ):
Число называется модулем сравнения.
Определение сравнимости чисел и по модулю равносильно любому из следующих утверждений:
Разность чисел и делится на без остатка; 
Число может быть представлено в виде 
, где 
— некоторое целое число.
Например : 32 и −10 сравнимы по модулю 7, так как оба числа при делении на 7 дают остаток 4:
Также, 32 и −10 сравнимы по модулю 7, так как их разность 42 делится на 7, и к тому же имеет место представление:
Видео:✓ Сравнение по модулю. Арифметика остатков | Ботай со мной #034 | Борис ТрушинСкачать
Сравнение чисел по модулю
Определение 1. Если два числа 1 ) a и b при делении на p дают один и тот же остаток r, то такие числа называются равноостаточными или сравнимыми по модулю p.
Утверждение 1. Пусть p какое нибудь положительное число. Тогда всякое число a всегда и притом единственным способом может быть представлено в виде
| a=sp+r, | (1) |
где s — число, и r одно из чисел 0,1, . p−1.
1 ) В данной статье под словом число будем понимать целое число.
Действительно. Если s получит значение от −∞ до +∞, то числа sp представляют собой совокупность всех чисел, кратных p. Рассмотрим числа между sp и (s+1)p=sp+p. Так как p целое положительное число, то между sp и sp+p находятся числа
  |
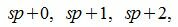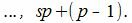Но эти числа можно получить задав r равным 0, 1, 2. p−1. Следовательно sp+r=a получит всевозможные целые значения.
Покажем, что это представление единственно. Предположим, что p можно представить двумя способами a=sp+r и a=s1p+r1. Тогда
 |
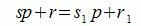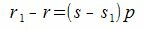 | (2) |
Так как r1 принимает один из чисел 0,1, . p−1, то абсолютное значение r1−r меньше p. Но из (2) следует, что r1−r кратно p. Следовательно r1=r и s1=s.
Число r называется вычетом числа a по модулю p (другими словами, число r называется остатком от деления числа a на p).
Утверждение 2. Если два числа a и b сравнимы по модулю p, то a−b делится на p.
Действительно. Если два числа a и b сравнимы по модулю p, то они при делении на p имеют один и тот же остаток p. Тогда
 |
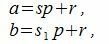где s и s1 некоторые целые числа.
Разность этих чисел
 | (3) |
делится на p, т.к. правая часть уравнения (3) делится на p.
Утверждение 3. Если разность двух чисел делится на p, то эти числа сравнимы по модулю p.
Доказательство. Обозначим через r и r1 остатки от деления a и b на p. Тогда
 |
 |
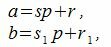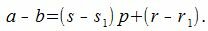По утверждению a−b делится на p. Следовательно r−r1 тоже делится на p. Но т.к. r и r1 числа 0,1. p−1, то абсолютное значение |r−r1| Свойство 1. Для любого a и p всегда
| a≡a mod (p). |
Свойство 2. Если два числа a и c сравнимы с числом b по модулю p , то a и c сравнимы между собой по тому же модулю, т.е. если
| a≡b mod (p), b≡c mod (p). |
| a≡c mod (p). |
Действительно. Из условия свойства 2 следует a−b и b−c делятся на p. Тогда их сумма a−b+(b−c)=a−c также делится на p.
| a≡b mod (p) и m≡n mod (p), |
| a+m≡b+n mod (p) и a−m≡b−n mod (p). |
Действительно. Так как a−b и m−n делятся на p, то
| (a−b)+ (m−n)=(a+m)−(b+n) , |
| (a−b)−(m−n)=(a−m)−(b−n) |
также делятся на p.
Это свойство можно распространить на какое угодно число сравнений, имеющих один и тот же модуль.
| a≡b mod (p) и m≡n mod (p), |
| am≡bn mod (p). |
Действительно.Так как a−b делится на p, то (a−b)m также делится на p, следовательно
| am≡bm mod (p). |
Далее m−n делится на p, следовательно b(m−n)=bm−bn также делится на p, значит
| bm≡bn mod (p). |
Таким образом два числа am и bn сравнимы по модулю с одним и тем же числом bm, следовательно они сравнимы между собой (свойство 2).
| a≡b mod (p). |
| a k ≡b k mod (p). |
где k некоторое неотрицательное целое число.
Действительно. Имеем a≡b mod (p). Из свойства 4 следует
| a·a≡b·b mod (p). |
| a·a·a≡b·b·b mod (p). |
| . |
| a k ≡b k mod (p). |
Все свойства 1-5 представить в следующем утверждении:
Утверждение 4. Пусть f(x1, x2, x3, . ) целая рациональная функция с целыми коэффициентами и пусть
| a1≡b1, a2≡b2, a3≡b3, . mod (p). |
| f(a1, a2, a3, . )≡f(b1, b2, b3, . ) mod (p). |
При делении все обстоит иначе. Из сравнения
| am≡bm mod (p) |
не всегда следует сравнение
| a≡b mod (p). |
Утверждение 5. Пусть
| am≡bm mod (p), |
| a≡b mod (p/λ), |
Доказательство. Пусть λ наибольший общий делитель чисел m и p. Тогда
| m=m1λ и k=k1λ. |
Так как m(a−b) делится на k, то
 |
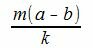имеет нулевой остаток. Тогда
  . |
 |
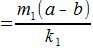имеет нулевой остаток, т.е. m1(a−b) делится на k1. Но числа m1 и k1 числа взаимно простые. Следовательно a−b делится на k1=k/λ и, тогда, a≡b mod (p/λ).
Утверждение 6. Если
| a≡b mod (p) |
и m является один из делителей числа p, то
| a≡b mod (m). |
Действительно. a−b делится на p. p делится на m. Следовательно a−b делится на m.
Утверждение 7. Если
| a≡b mod (p), a≡b mod (q), a≡b mod (s) |
| a≡b mod (h), |
где h наименьшее общее кратное чисел p,q,s.
Действительно. Разность a≡b должна быть числом, кратным p,q,s. и, следовательно должна быть кратным h.
В частном случае, если модули p,q,s взаимно простые числа, то
| a≡b mod (h), |
Заметим, что можно допустить сравнения по отрицательным модулям, т.е. сравнение a≡b mod (p) означает и в этом случае, что разность a−b делится на p. Все свойства сравнений остаются в силе и для отрицательных модулей.
Видео:Сравнение по модулю (Теория и примеры)Скачать
Решение сравнений и их приложения.
Решение сравнений и их приложения
Видео:Теория чисел. 6. Методы решения сравнений 1 й степениСкачать
Скачать:
| Вложение | Размер |
|---|---|
| reshenie_sravnenii_i_ih_prilozheniya.docx | 131.78 КБ |
Видео:Теория чисел. 4. Сравнения. Свойства сравненийСкачать
Предварительный просмотр:
Решение сравнений и их приложения.
Глава1. Общие вопросы теории сравнений
§1. Сравнение по модулю
§2. Свойства сравнений
- Свойства сравнений, не зависящие от модуля
- Свойства сравнений, зависящие от модуля
§3. Система вычетов
- Полная система вычетов
- Приведённая система вычетов
§4. Теорема Эйлера и Ферма
- Функция Эйлера
- Теорема Эйлера и Ферма
Глава2. Теория сравнений с переменной
§1. Основные понятия, связанные с решением сравнений
- Корни сравнений
- Равносильность сравнений
- Теорема Вильсона
§2. Сравнения первой степени и их решения
- Метод подбора
- Способы Эйлера
- Метод алгоритма Евклида
- Метод цепных дробей
§3. Системы сравнений 1-ой степени с одним неизвестным
§4. Деление сравнений высших степеней
§5. Первообразные корни и индексы
- Порядок класса вычетов
- Первообразные корни по простому модулю
- Индексы по простому модулю
Глава3. Приложение теории сравнений
§1. Признаки делимости
§2. Проверка результатов арифметических действий
§3. Обращение обыкновенной дроби в конечную
десятичную систематическую дробь
В нашей жизни часто приходится сталкиваться с целыми числами и задачами связанными с ними. В данной дипломной работе я рассматриваю теорию сравнения целых чисел.
Два целых числа, разность которых кратна данному натуральному числу m называются сравнимыми по модулю m.
Слово «модуль» происходит от латинского modulus, что по–русски означает «мера», «величина».
Утверждение «а сравнимо с b по модулю m» обычно записывают в виде a b (mod m) и называют сравнением.
Определение сравнения было сформулировано в книге К. Гаусса «Арифметические исследования». Эту работу, написанную на латинском языке начали печатать в 1797 году, но книга вышла в свет лишь 1801 году из-за того, что процесс книгопечатания в то время был чрезвычайно трудоёмким и длительным. Первый раздел книги Гаусса так и называется: «О сравнении чисел вообще».
Сравнениями очень удобно пользоваться в тех случаях, когда достаточно знать в каких – либо исследованиях числа с точностью до кратных некоторого числа.
Например, если нас интересует, на какую цифру оканчивается куб целого числа a, то нам достаточно знать a лишь с точностью до кратных чисел 10 и можно пользоваться сравнениями по модулю 10.
Целью данной работы является рассмотрение теории сравнений и исследование основных методов решения сравнений с неизвестными, а также изучение применения теории сравнений к школьной математике.
Дипломная работа состоит из трёх глав, причём каждая глава разбита на параграфы, а параграфы на пункты.
В первой главе изложены общие вопросы теории сравнений. Здесь рассматриваются понятие сравнения по модулю, свойства сравнений, полная и приведённая система вычетов, функция Эйлера, теорема Эйлера и Ферма.
Вторая глава посвящена теории сравнений с неизвестной. В ней излагаются основные понятия, связанные с решением сравнений, рассматриваются способы решения сравнений первой степени ( метод подбора, способ Эйлера, метод алгоритма Евклида, метод цепных дробей, с помощью индексов), систем сравнений первой степени с одной неизвестной, сравнений высших степеней и др.
Третья глава содержит некоторые приложения теории чисел к школьной математике. Рассмотрены признаки делимости, проверка результатов действий, обращение обыкновенных дробей в систематические десятичные дроби.
Изложение теоретического материала сопровождается большим количеством примеров, раскрывающих суть вводимых понятий и определений.
🎬 Видео
Решение сравнений первой степениСкачать
Т.чисел 9. Система сравнений Метод подстановкиСкачать
Сравнения по модулю: решение задач №1 | Vasily mathsСкачать
Т.чисел 10. Система сравнений. Два метода решенияСкачать
СРАВНЕНИЕ ПО МОДУЛЮ 😉 #shorts #егэ #огэ #математика #профильныйегэСкачать
Т.чисел 8. Система сравнений. Китайская теорема об остаткахСкачать
Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать
ПРостой стрим. Олимпиадная теория чисел в течение 12 часов!Скачать
Модуль числа. 6 класс.Скачать
Теория чисел. 7. Решаем сравнения 1 й степениСкачать
Арифметика остатковСкачать
Теория чисел. Сравнение первой степени. Метод подходящих дробейСкачать
Малая теорема Ферма и теорема Эйлера | Ботай со мной #037 | Борис Трушин !Скачать
Доказываем сравнение по модулю 37 | Теория чисел | КАК РЕШАТЬ?Скачать
Признаки делимости | Сравнение по модулю | Ботай со мной #035 | Борис Трушин !Скачать
МодульСкачать
