Теория о структуре общего решения линейного однородного уравнения n го порядка

Фундаментальная система решений линейного однородного дифференциального уравнения. Теорема о структуре общего решения решений линейного однородного дифференциального уравнения. В этом разделе мы докажем, что базисом линейного пространства частных решений однородного уравнения может служить любой набор из n его линейно независимых решений.

Опр. 14.5.5.1. фундаментальной системы решений. Фундаментальной системой решений линейного однородного дифференциального уравнения n-го порядка называется любая линейно независимая система y1(x), y2(x), …, yn(x) его n частных решений.

Теорема 14.5.5.1.1 о структуре общего решения линейного однородного дифференциального уравнения. Общее решение y(x) линейного однородного дифференциального уравнения есть линейная комбинация функций из фундаментальной системы решений этого уравнения:

y(x) = C1 y1(x) + C2 y2(x) + …+ Cn yn(x).

Док-во. Пусть y1(x), y2(x), …, yn(x) — фундаментальная система решений линейного однородного дифференциального уравнения. Требуется доказать, что любое частное решение yчо(x) этого уравнения этого уравнения содержится в формуле y(x) = C1 y1(x) + C2 y2(x) + …+ Cn yn(x) при некотором наборе постоянных C1, C2, …, Cn. Возьмём любую точку , вычислим в этой точке числа и найдём постоянные C1, C2, …, Cn как решение линейной неоднородной системы алгебраических уравнений

Такое решение существует и единственно, так как определитель этой системы равен . Рассмотрим линейную комбинацию y(x) = C1 y1(x) + C2 y2(x) + …+ Cn yn(x) функций из фундаментальной системы решений с этими значениями постоянных C1, C2, …, Cn и сравним её с функцией yчо(x). Функции y(x) и yчо(x) удовлетворяют одному уравнению и одинаковым начальным условиям в точке x0, следовательно, по единственности решения задачи Коши, они совпадают: yчо(x) = C1 y1(x) + C2 y2(x) + … + Cn yn(x). Теорема доказана.

Из этой теоремы следует, что размерность линейного пространства частных решений однородного уравнения с непрерывными коэффициентами не превышает n. Осталось доказать, что эта размерность не меньше n.

Теорема 14.5.5.1.2 о существовании фундаментальной системы решений линейного однородного дифференциального равнения. Любое линейное однородное дифференциальное уравнение n -го порядка с непрерывными коэффициентами имеет фундаментальную систему решений, т.е. систему из n линейно независимых решений.

Док-во. Возьмём любой числовой определитель n -го порядка, не равный нулю

.

Возьмём любую точку и сформулируем для уравнения (21) n задач Коши, причём начальные условия в точке x0 для i-ой задачи возьмём из i-го столбца этого определителя:

Пусть y1(x), y2(x), …, yn(x) — решения этих задач. Эта система линейно независима на (a, b), так как её определитель Вронского в точке x0 равен взятому числовому определителю и отличен от нуля, следовательно, это фундаментальная система решений. Теорема доказана.

Итак, мы доказали, что размерность линейного пространства частных решений однородного уравнения с непрерывными коэффициентами равна n, и базисом в этом пространстве служит любая фундаментальная система решений. Общее решение такого уравнения равно линейной комбинации функций из фундаментальной системы решений. Остаётся вопрос — как находить фундаментальную систему решений; оказывается, что в общем случае это возможно только в случае уравнения с постоянными коэффициентами. Мы займёмся этим дальше; предварительно рассмотрим ещё ряд свойств решений однородного уравнения.

Видео:Теорема о структуре общего решения линейного однородного дифференциального уравненияСкачать

Фундаментальная система решений. Теорема о структуре общего решения линейного однородного уравнения n-го порядка

Функции называются линейно зависимыми на , если существуют числа , из которых хотя бы одно не равно нулю, такие, что . (4)

Если тождество (4) выполняется лишь в случае, когда все , то функции называются линейно независимыми на . Система из линейно независимых на интервале решений однородного дифференциального уравнения -го порядка (3) с непрерывными на коэффициентами называется фундаментальной системой решений этого уравнения.

Чтобы решить линейное однородное дифференциальное уравнение -го порядка (3) с непрерывными коэффициентами , надо найти его фундаментальную систему решений.

Согласно теореме, произвольная линейная комбинация из решений , т. е. сумма

где — произвольные числа, есть в свою очередь решение уравнения (3) на . Таким образом, общее решение однородного дифференциального уравнения (3) имеет вид (5), где — произвольные постоянные, а — частные решения (3), образующие фундаментальную систему решений однородного уравнения.

Видео:Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентамСкачать

Разностные уравнения, определение порядка уравнения

РАЗНОСТНЫЕ УРАВНЕНИЯ [difference equations] — уравнения, содержащие конечные разности искомой функции. (Конечная разность определяется как соотношение, связывающее дискретный набор значений функции y = f(x), соответствующих дискретной последовательности аргументов x₁, x₂, . x_n.) В экономических исследованиях значения величин часто берутся в определенные дискретные моменты времени. Напр., о выполнении плана судят по показателям на конец планируемого периода. Поэтому вместо скорости изменения какой-либо величины df/dt приходится брать среднюю скорость за определенный конечный интервал времени Дf/Дt. Если выбрать масштаб времени так, что длина рассматриваемого периода равна 1, то скорость изменения величины можно представить как разность

которую часто называют первой разностью. При этом различают правую и левую разности, в частности

— левая, а приведенная выше — правая. Можно определить вторую разность:

Д(Дy) = Дy(t + 1) — Дy(t) = y(t + 2) —

и разности высших порядков

Теперь можно определить Р. у. как уравнение, связывающее между собой конечные разности в выбранной точке:

f [y(t), Дy(t), . Д n y(t)] = 0.

Р. у. всегда можно рассматривать как соотношение, связывающее значения функции в ряде соседних точек

При этом разность между последним и первым моментами времени называется порядком уравнения.

При численном решении дифференциальных уравнений их часто заменяют разностными. Это возможно, если решение Р. у. стремится к решению соответствующего дифференциального уравнения, когда интервал Дt стремится к нулю.

Видео:Теорема о структуре общего решения линейного неоднородного дифференциального уравненияСкачать

Теорема о структуре общего решения ЛОДУ (док). Понятие ФСР

Опр: Система n линейно-независимого решения ЛОДУ n-го порядка называется ФСР

Теорема о структуре общего решения ЛОДУ

Если функции y₁(х)_, y₂(х)_, … ,y_n(х) – образует ФСР ЛОДУ у ( n ) + P₁y ( n -1) +…+ P_n-1 y’ + P_n y = 0 , то y(х) = C₁y₁(x) + C₂y₂(x) + … + C_ny_n(x) = , есть общее решение этого уровня. (4).

Из теоремы о неравенстве нулю вронскиана линейно-независимых решений ЛОДУ:

Если n решений y_1, y_2, … ,y_n ЛОДУ (2) и они линейно-независимы, на интервале (а,b) то определитель Вронского не может обращаться в ноль (0) ни в одной точке х ‌| для любого Х из (а,b) .

ð что (4) являются решением у ( n ) + P₁y ( n -1) +…+ P_n-1 y’ + P_n y = 0

остается доказать, что можно подобрать const-ты то С₁, С₂, … С_n , таким образом что функция (4) удовлетворяет любой системе начальных условий [н.у.]

Задаем н.у. , при x₀ (а,b) y(х₀) = y₀, y’(х₀) = y₀’, y ( n -1) (x₀) = y₀ ( n -1) определяем C_1,C₂,…, C_n

Определение:

Определителем этой системы является определитель Вронского

W[y_1, y_2, … ,y_n] 0, C_1,C₂,…, C_n — определяется един-м образом

Построим = C₁y₁(x) + C₂y₂(x) + … + C_ny_n(x) ,

согласно свойству (если y₁) α₁y₁ + α₂y₂ + …+ α_ny_n = 0 причем хотя бы одно h_i 0.

— является решением ДУ(2) = y(x) , т.к. система (5) определена теми же н.у., что и y(x) ч.т.д.

1) максимальное число линейно-независимых решение ЛОДУ, коэффициенты непрерывны на (a,b) равно порядку этого уравнения.

2) независимо от н.у. все другие решения таких уравнений ЛОДУ является линейной комбинацией этих независимых решений (решений ФС)

3) Пространство решений ЛОДУ n-го порядка имеет базис из n-векторов, т.е. пространство n-мерное.

4) Для решения ЛОДУ n-го порядка необходимо найти ФСР. Общее решение получается как линейная комбинация решений ФС.

11. Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентами. Вид частных решений, характеристическое уравнение(×)

ЛОДУ с постоянными коэффициентами

у ( n ) + P₁y ( n -1) +…+ P_n-1 y’ + P_n y = 0, где все P_i (i= 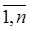)= const

будем искать частное решение y=e kx , к – неизвестная постоянная

y ( n ) =k ( n ) e kx

k (n) e kx + P₁k (n-1) e kx + … + P_ne kx = e kx (k (n) + P₁k (n-1) + … + P_n) = 0

e kx 0 => k (n) + P₁k (n-1) + … + P_n = 0, (1)

ð y=e kx — решение ДУ

(1) – характеристическое уравнение для ЛОДу с постоянными коэффициентами, выражения слева характеристический многочлен.

Решением характеристич уравнения (1) дает систему частных решений ЛОДу, структура ФСР зависит от вида корней характер уравнения.

(1) – алгебраическое уравнение n-ой степени, может иметь не более, чем n корней, обознач-м эти корни характеристического уравнения через k₁ ,k₂ …k_n

1)все корни хар-го уранения вещественны и различны

2)все корни различны, но среди них есть комплексные

3)среди действительных корней имеются кратные

4)среди комплексных корней есть кратные

Общий алгоритм решения ЛОДу с постоянным коэффициентом

1) составим характер уравнение : y=e kx , k ( n ) + P₁k ( n -1) + … + P_n = 0

2) найти корни характер уравнения k₁ ,k₂ …k_n

3) по характеру корней находим частное линейно-независимое решение по таблице 1

4) подставляем частное решение на основе Теоремы о структуре общего решения ЛОДУ и получаем общее решение y =

№	Вид корня	Соответственное решение
Действ корень кратности 1	e kx
Пара корней a bi;кратнос 1	e а x cosbx , e а x sinbx
Действит корень кратност α	e kx , хe kx , х 2 e kx , х 3 e kx ,…, х α-1 e kx
Пара сопряж корней α a bi	e а x cosbx , e а x sinbx хe а x cosbx , хe а x sinbx х 2 e а x cosbx , х 2 e а x sinbx х α-1 e а x cosbx , х α-1 e а x sinbx

13. Линейные неоднородные дифференциальные уравнения n-го порядка. Теорема о структуре общего решения (док. для n=2). Теорема о суперпозиции решений (док. для n=2).

у ( n ) + P₁y ( n -1) +…+ P_n-1 y’ + P_n y = f(x) (1) P_i – непрерывна на отрезке (a,b)

Теорема о структуре общего решения ЛНДУ

Общее решение ЛНДУ есть сумма частного решения и общего решения соответственного ему однородного уравнения

Для уравнения 2-го порядка ( но теорема применима для уравнений любого порядка)

Обозначим у*(х) – частное решение ЛНДУ

(х) – общее решение ЛОДУ

(2) у= у*+ — общее решение ЛНДУ

Дважды дифференцируем функцию (2) и подставляем у, y’,y” в (1’)

у*”(x) + ”(x) + P₁(x)[ у*(x)+ ’(x)] + P₂(x)[ у*(x)+ (x)] =

= [у*”(x)+ P₁(x) у*’(x)+ P₂(x) у*(x)] + [ ”(x) + P₁(x) ’ (x)+ P₂(x) (x)] = f(x) + 0 = 0

= C₁y₁(x) + C₂y₂(x), y_1,y₂ – частное решение ЛОДУ y” + P₁y’ + P₂ = 0

C₁C₂ – подбираем так, чтобы они удовлетворяли начальным условиям

y(x₀)=y₀ , y’(x₀)=y₀’, для любых х₀ (а,в), и любых y₀ ,y₀’

Линейная неоднородная система, определитель этой системы, определитель Вронского

W[y_1, y₂]≠0 =>система имеет единственное решение при любых ₀ , ’₀ ,y*_{0 ,}y*’₀ , это означает у= у*+ — общее решение ЛНДУ

Теорема2 принцип суперпозиции (принцип сложения решений)

Если функция y_i(x) является решением ЛНДУ

(3) y ( n ) + P₁y ( n -1) + … + P_ny = f_i(x) то функция = α₁y₁ + α₂y₂ + … + α_ny_n , то это функция является решением y ( n ) + P₁y ( n -1) + … + P_ny = α₁ f₁(x) + α₂ f₂(x) + … + α_n f_n(x) (4)

Подставим y, y’, y”, в (4) , учитываем что y₁ y₂ решение соответственного уравнения (3)

14. Линейные неоднородные дифференциальные уравнения n-го порядка с постоянными коэффициентами. Метод неопределенных коэффициентов для уравнений со специальной правой частью. Метод вариации произвольных постоянных (вывод рабочей формулы).

Рассмотрим ЛНДУ с постоянными коэф-ми.

Метод неопр-х коэф-в можно применять если правое ур-е имеет следующий вид: f(x)= , , -многочлены степени g и r соотв-но a и b некоторые числа. В основе метода неопр-х коэф-в лежит знание формы частного решения, а именно частное решение стоит искать в аналогич-ой форме свободного члена.

№	Вид правой части (f(x))	Корни харак-го уравнения	Вид частного решения y*
P (x)=A x +A x +… +A x+ A	а) число 0 не явл-ся корнем хар-го ур-я б) число 0 явл-ся корнем хар-го ур-я кратности	а) y*=b x +b x +…+ +b б) y*=x (B x +B x +… +B )
P (x)e = e ( A x + +A x +…+A x+ A ) p-действ-е число	а) число p не явл-ся корнем хар-го ур-я б) число p явл-ся корнем хар-го ур-я кратности	a) y*= e ( b x +b x +…+ +b ) б) y*= e x ( b x +b x +…+ +b )
P (x)cosgx+Q (x)singx g-число	а) число gi-не явл-ся корнем хар-го ур-я б) число gi-явл-ся корнем хар-го ур-я кратности	а) y*= (x)cosgx+ (x)singx б) y*=x ( (x)cosgx+ (x)singx)
P (x)e cosgx+ Q (x)e singx	а) число gi-не явл-ся корнем хар-го ур-я б) число gi-явл-ся корнем хар-го ур-я кратности	а) y*= (x) e cosgx+ (x)singx б) y*= x ( (x) e cosgx+ + (x)singx)

Замечание к таблице: 1)степени многоч-ов P и Q в случаях (3) и (4) можно считать одинаковыми, если они различны, то коэф-ты при недостающих степенях одного из многоч-ов можно считать=0.

2)правая часть ур-я может содержать несколько слагаемых; в этом случае сост-ся из неск-ких слагаемых в соотв-ии с Теоремой о неравенстве нулю вронскиана линейно-независимых решений ЛОДУ

Метод вариации производных постоянных(метод Лагранджа).

Метод позволяет найти решение ДУ независимо от вида правой части, когда известно общее решение соотв-го однородного ДУ.

Например: ДУ 2-го порядка. Пусть y”+P (x)y’+P (x)y=f(x) (1) пусть y (x) и y (x)-ФСРЛОДУ

y”+P (x)y’+P (x)y=0 (x)= C y (x)+C y (x) (2). Частное решение y*(x) в виде (14) считая при этом C и C не постоянными, а неизв-ми функциями от x.

y*= C (x)y (x)+C (x)y (x), y*= C’ (x)y (x)+C(x) y’ (x)+C’ (x)y (x)+ C(x) y’ (x)

Пусть C (x) и C (x) C’ (x)y (x)+ C’ (x)y (x)=0 /справедливое равенство (3), тогда y* ’= C (x)y’ (x)+ C (x)y’ (x); y* ”= C (x)y’ (x)+ C (x)y” (x)+ C’ (x)y’ (x)+ C (x)y” (x).

Подставим y*, y* ’, y* ” в (1): C (x)[ y” (x) + P (x)y ’(x) + P (x) y (x)] + C (x)[ y” (x) + P (x)y ’(x) + P (x) y (x)] + C’ (x)y’ (x)+ C’ (x)y’ (x)=f(x). Т.к. y (x), y (x) решения ОДУ, то выражения []=0 C’ (x)y’ (x) + C’ (x)y’ (x)=0.

Объясним два условия и (3):

C’ (x)y (x)+ C’ (x)y (x)=0

C’ (x)y’ (x)+ C’ (x)y’ (x)=f(x) (4)

Неопр-е ф-ии C’ (x) и C’ (x).

Определитель этой системы: W[y , y ]= 0 решая систему мы получим C (x)= (x),

C (x)= (x) проинтегрируем и получим решение C (x) и C (x) найдены. Подставим в y*.

Для ЛНДУ n-го порядка ф-ии C 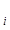(x) определяются из системы:

C’ (x)y + C’ (x)y +…+ C’ (x)y =0

C’ (x)y’ + C’ (x)y’ +…+ C’ (x)y’ =0

C’ (x)y + C’ (x)y +…+ C’ (x)y =0

C’ (x)y + C’ (x)y +…+ C’ (x)y =f(x)

Алгоритм решения ЛНДУ

1) найти ФСР однородного уравнения и записать его общее решение (ОУ)

2) записать частное решение неоднородного ДУ в форме общего решения ОУ считая C_i=C_i (x)

3) построить систему для определения C_i ‘(x) – решить ее

4) найти C_i (x) и подставить их в общее решение НДУ

🎦 Видео

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

15. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать

15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Теорема о структуре общего решения однородной системы линейных уравненийСкачать

Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Скачать

16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Видеоурок "Линейные однородные диф. уравнения n-го порядка"Скачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Решение линейного однородного дифференциального уравнения. Практическая часть. 11 класс.Скачать

19. Общее решение линейного уравненияСкачать

Однородное линейное дифференциальное уравнение. Алгоритм решенияСкачать

Дифференциальные уравнения, 3 урок, Однородные уравненияСкачать

4. Однородные дифференциальные уравнения (часть 1)Скачать