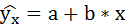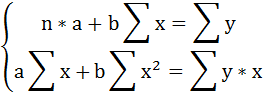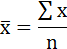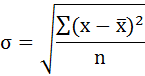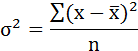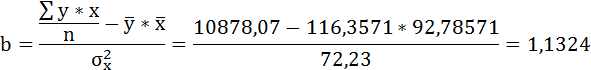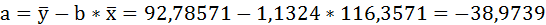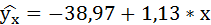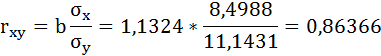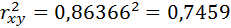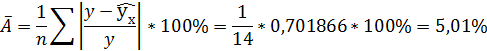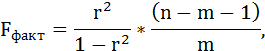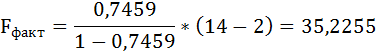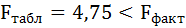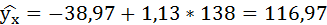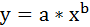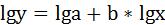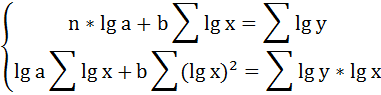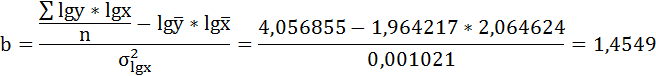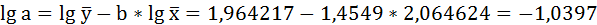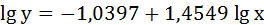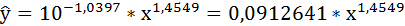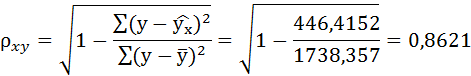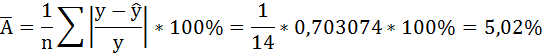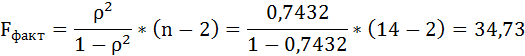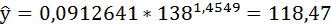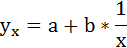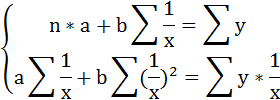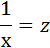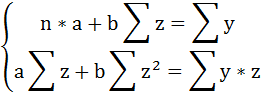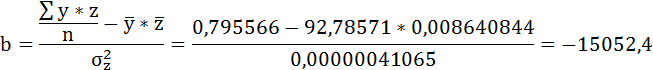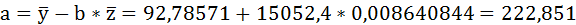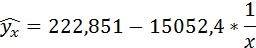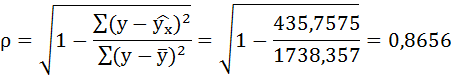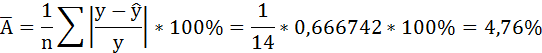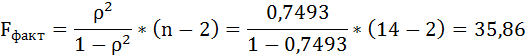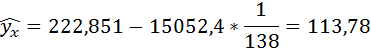Теории статистики при построении уравнения регрессии используют следующие оценки значимости (3 видео)

V1: Многомерный статистический анализ

S: Связь между признаками можно признать существенной при значении линейного коэффициента корреляции …

S: В теории статистики по аналитическому выражению выделяют следующие виды связей между признаками:

S: В теории статистики при исследовании взаимосвязи признаков, выраженных в ранжированной форме, используются следующие коэффициенты:

+: ранговый коэффициент корреляции Кендалла

+: коэффициент корреляции рангов Спирмена

S: В теории статистики показатель «коэффициент корреляции» характеризуют следующие утверждения:

+: принимает значения в интервале [-1; 1]

+: показатель тесноты линейной корреляционной зависимости

S: В теории статистики показатель «коэффициент детерминации» характеризуют следующие утверждения:

+: универсальный показатель стохастической зависимости

+: принимает значения в интервале [0; 1]

S: В теории статистики при построении уравнения регрессии используют следующие оценки значимости:

+: уравнения в целом (по критерию Фишера)

+: коэффициентов регрессии (по критерию Стьюдента)

S: Закончите предложение.

Связь является функциональной, если определенному значению факторного признака соответствует … .

+: строго определенное значение результативного признака

S: Коэффициент ассоциации определяется для:

+: двух качественных признаков, каждый из которых состоит из двух групп

S: Если линейный коэффициент корреляции имеет положительное значение, то значение коэффициента регрессии…

S: Для определения степени тесноты связи между качественными признаками используется:

S: Коэффициент детерминации представляет собой долю:

+: дисперсии зависимой переменной , объясняемой регрессией в общей дисперсии

S: По направлению связи в статистике классифицируются на:

+: прямые и обратные

S: Оценка значимости коэффициента регрессии осуществляется с помощью:

+: t – критерия Стъюдента

S: Если коэффициент корреляции равен нулю, то это означает:

S: Коэффициент детерминации изменяется в пределах:

S: Связь между -: У и -: Х можно признать существенной, если значение линейного коэффициента корреляции равно:

S: Согласно теории статистики установите соответствие между показателями и их содержанием:

L1: парный коэффициент корреляции

L2: множественный коэффициент корреляции

L3: коэффициент конкордации

L4: частный коэффициент корреляции

R3: показатель связи между произвольным числом ранжированных признаков

R1: показатель связи между двумя количественными признаками

R2: показатель связи между одним и множеством других количественных признаков

R:4 показатель связи между количественными результативным и факторным признаками при элиминированном влиянии других факторных признаков

S: Согласно теории статистики установите соответствие между значениями коэффициента корреляции и смысловой интерпретацией связи:

R3: связь обратная, практически отсутствует

R1: связь обратная умеренная

R4: связь прямая сильная

R2: показатель не имеет смысла

S: Согласно теории статистики установите соответствие между классификационными признаками и видами корреляционной связи:

L1: теснота связи

L2: направление связи

L3: аналитическое выражение связи

L4: число взаимосвязанных статистических признаков

R2: прямая, обратная

R3: линейная, нелинейная

R1: практически отсутствующая, слабая, умеренная, сильная

R4: парная, множественная

S: Согласно теории статистики установите соответствие между видами переменных и используемыми показателями взаимосвязи:

L1: факторный и результативный признаки выражены количественными переменными

L2: несколько факторных и результативный признаки выражены количественными переменными

L3: факторный и результативный признаки выражены ранговыми переменными

L4: признаки являются альтернативными

R3: ранговый коэффициент корреляции Спирмена

R4: коэффициенты ассоциации и контингенции

R2: коэффициент конкордации

R1: парный коэффициент корреляции Пирсона

S: Согласно теории статистики установите соответствие между показателями взаимосвязи и условиями их применения:

L1: парный коэффициент корреляции Пирсона

L2: коэффициент конкордации

L3: коэффициент ассоциации

L4: корреляционное отношение

R4: линейная или нелинейная связь между двумя количественными признаками

R2: связь между двумя и более ранговыми переменными

R1: линейная связь между двумя количественными признаками

R3: связь между альтернативными признаками

S: Связь между признаками является функциональной, если значение линейного коэффициента корреляции равно … .

S: Определение параметров уравнения регрессии между двумя признаками является целью:

S: Расчет коэффициента детерминации невозможен без значения коэффициента:

S: Связи в статистике по направлению бывают:

S: Термин «регрессия» предложил…

S: Первое в истории регрессионное исследование ставило своей целью выявление зависимостей между:

+: ростом отцов и сыновей

S: Выберите верное утверждение:

+: при тесной корреляционной связи между признаками причинно-следственная связь между процессами, которые они характеризуют, может как наличествовать, так и отсутствовать;

S: В теории статистики явление, при котором два признака демонстрируют тесную корреляционную связь, но при этом характеризуемые ими процессы вообще не связаны причинно-следственной связью, называется:

V1: Статистика населения

S: Сведения о численности, составе и размещении населения берутся из:

S: Если численность населения на 1 января текущего года 12 тыс. чел., на 1 апреля текущего года 11тыс. чел., на 1 июля текущего года 13 тыс. чел., на 1 октября текущего года 12,5 тыс.чел., на 1 января следующего года 12 тыс. чел., то средняя численность населения муниципального образования равна (Результат округлить до целого и ввести в виде числа без указания единиц измерения).

S: В течение анализируемого периода времени в области родилось 600 человек, умерло 900 человек. Средняя численность населения области 30000 человек. Коэффициент рождаемости населения области равен промилле .

S: В течение анализируемого периода времени в область прибыло из других областей 100 человек, а выбыло с территории 300 человек. Средняя численность населения области составляла 30000 человек. Коэффициент выбытия равен промилле .

S: Лица старше 16 лет, которые в отчетный период времени выполняли работу по найму на условиях полного и неполного рабочего дня, временно отсутствовали на работе из-за болезни, в связи с отпуском и по другим причинам, установленным законодательством, либо выполняли работу без оплаты в семейном предприятии, относятся к:

S: Численность населения на начало года – 126 тыс. чел. В течение года: родилось 1,89 тыс. чел., умерло 1,26 тыс. чел., заключено браков 2,52 тыс. чел., зарегистрировано разводов – 3,78 тыс. чел., прибыло – 0,63 тыс. чел., убыло – 0,5 тыс. чел. Коэффициент брачности составляет:

S: В течение анализируемого периода времени в область прибыло из других областей 600 человек, а выбыло с территории 300 человек. Средняя численность населения области составляла 30000 человек. Коэффициент прибытия равен промилле .

S: По нижеприведенным данным определить среднюю численность населения за период 2002-2005 гг.

S: К наличному населению относятся:

+: лица, фактически находящиеся в данном пункте

S: В отечественной практике для выделения городских населенных пунктов используется:

S: Численность умерших в среднем на каждую 1000 человек населения отражает ________________ коэффициент смертности.

S: Численность прибывших и выбывших на 1000 человек населения отражает:

+: коэффициент интенсивности миграционного оборота

S: Процессы эмиграции населения из страны характеризует:

+: значение коэффициента выбытия населения

S: Статистика населения изучает два вида движения населения:

S: В статистике населения механическое движение населения характеризуют следующие из нижеприведенных абсолютных показателей:

S: В статистике населения для вычисления коэффициента пенсионной нагрузки используют следующие данные:

+: численность населения старше трудоспособного возраста

+: численность населения в трудоспособном возрасте

S: В статистике населения показатель «миграционный прирост населения» характеризуют следующие утверждения:

+: абсолютный показатель механического движения населения

+: разность числа прибывших и числа выбывших в течение года

S: В статистике населения сущность показателя «общий коэффициент разводимости» характеризуют следующие утверждения:

+: относительный показатель естественного движения населения

+: отношение числа расторгнутых браков к среднегодовой численности населения

S: Возрастные интервалы в половозрастной группировке населения бывают:

S: Характеристиками изменения состава населения служат коэффициенты …

S: В статистике населения общий коэффициент брачности характеризуют следующие утверждения:

+: отношение числа заключенных браков в течение года к среднегодовой численности населения

S: В статистике населения при изучении численности и структуры населения используют следующие показатели:

+: показатели демографической нагрузки населения

+: средняя численность населения

S: К общим коэффициентам естественного движения населения относятся:

S: К частным коэффициентам движения населения относятся:

+: брутто-коэффициент воспроизводства населения

+: нетто-коэффициент воспроизводства населения

S: Соотнесите группу и вид характеристики, включаемой в программу переписи населения:

R3: Число лет обучения

R2: Источник доходов

S: Текущий учет населения в РФ осуществляют органы:

+: Залы актов гражданского состояния

S:В настоящее время единицей наблюдения в ходя переписей населения в России является:

S: Половозрастная пирамида населения говорит о депопуляции в том случае, если к основанию она…

S: В статистике населения все коэффициенты, характеризующие его движение, берутся в расчете на:

S: В практике статистики наиболее широко используемым видом демографических таблиц являются:

Содержание

Статистические методы моделирования связи социально-экономических явлений и процессов
Пример нахождения статистической значимости коэффициентов регрессии
Задача №1 Построение уравнения регрессии
Требуется:
Решение:
🔍 Видео

Видео:Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать

Статистические методы моделирования связи социально-экономических явлений и процессов

213. Задание <> ТЗ № 224

Согласно теории статистики установите соответствие между показателями и их содержанием

Парный коэффициент корреляции	Показатель связи между двумя количественными признаками
Множественный коэффициент корреляции	Показатель связи между одним и множеством других количественных признаков
Коэффициент конкордации	Показатель связи между произвольным числом ранжированных признаков
Частный коэффициент корреляции	Показатель связи между количественными результативным и факторным признаками при элиминированном влиянии других факторных признаков
Показатель связи между несколькими атрибутивными признаками

214. Задание <> ТЗ № 192

Согласно теории статистики установите соответствие между показателями взаимосвязи и условиями их применения

Парный коэффициент корреляции Пирсона	Линейная связь между двумя количественными признаками
Коэффициент конкордации	Связь между двумя и более ранговыми переменными
Коэффициент ассоциации	Связь между альтернативными признаками
Корреляционное отношение	Линейная или нелинейная связь между двумя количественными признаками
Связь между двумя и более атрибутивными признаками

215. Задание <> ТЗ № 193

Согласно теории статистики установите соответствие между классификационными признаками и видами корреляционной связи

Тесная связь	Практически отсутствует, слабая, умеренная, сильная
Направление связи	Прямая, обратная
Аналитическое выражение связи	Линейная, нелинейная
Число взаимосвязанных статистических признаков	Парная, множественная
Количественная, качественная

216. Задание <> ТЗ № 194

Согласно теории статистики уравнение регрессии характеризует следующие утверждения

R статистически значимо при значении критерия Фишера больше критического

£ отражает форму связи между альтернативными признаками

R отражает форму зависимости результативного признака от факторных признаков

£ статистически значимо при значении критерия Фишера меньше критического

217. Задание <> ТЗ № 195

В теории статистики при построении уравнения регрессии используют следующие оценки значимости

R коэффициентов регрессии (по критерию Стьюдента)

R уравнения в целом ( по критерию Фишера)

218. Задание <> ТЗ № 196

В теории статистики по аналитическому выражению выделяют следующие виды связей между признаками

219. Задание <> ТЗ № 197

По результатам статистического исследования получено значение коэффициента корреляции Пирсона, равное 0,8. В этом случае можно сделать вывод о том, что линейная связь

220. Задание <> ТЗ № 198

Согласно теории статистики корреляционное отношение характеризуют следующие утверждения

R изменяется в пределах от 0 до 1

£ позволяет установить наличие нелинейной связи

£ устанавливает связь между альтернативными признаками

R изменяется в пределах от 0 до 100%

221. Задание <> ТЗ № 199

Связь между Y и Х можно признать существенной, если значение линейного коэффициента корреляции равно

222. Задание <> ТЗ № 200

Коэффициент ассоциации определяется для

£ двух количественных признаков

£ одного количественного и одного качественного признаков

£ двух относительных признаков

R двух качественных признаков, каждый из которых состоит из двух групп

223. Задание <> ТЗ № 201

Знак «+» или «-» у коэффициента корреляции указывает на

R направление связи

224. Задание <> ТЗ № 202

Модель, в которой структурные компоненты ряда суммируются, называется

225. Задание <> ТЗ № 203

Модель, в которой результативный показатель равен произведению факторных называется

226. Задание <> ТЗ № 204

По аналитическому выражению корреляционные связи могут быть

227. Задание <> ТЗ № 205

В теории статистики при исследовании взаимосвязи от двух и более признаков используются следующие виды коэффициентов корреляции

228. Задание <> ТЗ № 206

В теории статистики функциональную зависимость среднего значения результативного признака от значения факторного признака характеризуют следующие утверждения

£ аналитически выражается дисперсионным уравнением

R это — корреляционная зависимость

£ это — вариационная зависимость

R аналитически выражается уравнением регрессии

229. Задание <> ТЗ № 207

Согласно теории статистики установите соответствие между показателями и их содержанием

Парный коэффициент корреляции	показатель связи между факторным и результативным признаками
множественный коэффициент корреляции	показатель связи между несколькими факторными и результативным признаками
ранговый коэффициент корреляции Спирмена	показатель связи между количественными или качественными признаками, при условии их ранжирования
коэффициент ассоциации	показатель связи между двумя альтернативными признаками
показатель связи между тремя атрибутивными признаками

230. Задание <> ТЗ № 208

Для выявления формы воздействия одних факторов на другие используется метод анализа

231. Задание <> ТЗ № 209

Корреляционное отношение используется для

£ выявления направления связи

£ определения тесноты связи

£ определения остаточной вариации

R определение факторной вариации

232. Задание <> ТЗ № 210

В теории статистики при исследовании взаимосвязи признаков, выраженных в порядковой шкале, используются следующие коэффициенты

£ коэффициент множественной корреляции Пирсона

R ранговый коэффициент корреляции Кендалла

£ коэффициент парной корреляции Присона

R коэффициент корреляции рангов Спирмена

233. Задание <> ТЗ № 211

Коэффициент детерминации изменяется в пределах

£ всех положительных чисел

234. Задание <> ТЗ № 190

Согласно теории статистики установите соответствие между значениями коэффициента корреляции и смысловой интерпретацией связи

-0,5	Связь обратная умеренная
1,9	показатель не имеет смысла
-0,1	Связь обратная, практически отсутствует
0,95	Связь прямая сильная
Связь прямая умеренная

235. Задание <> ТЗ № 191

Согласно теории статистики установите соответствие между видами переменных и используемыми показателями взаимосвязи

Факторный и результативный признаки выражены количественными переменными	Парный коэффициент корреляции Пирсона
Несколько факторных и результативных признаков выражены количественными переменными	Множественный и частные коэффициенты корреляции
Факторный и результативный признаки выражены ранговыми переменными	Ранговый коэффициент корреляции Спирмена
Признаки являются альтернативными	Коэффициент ассоциации и контингенции
Коэффициент конкордации

236. Задание <> ТЗ № 240

Коэффициент корреляции изменяется в пределах

£ всех положительных чисел

237. Задание <> ТЗ № 241

В практике статистики для вычисления средних интервального ряда используют следующие данные

R середины интервалов

R частоты (частости)

£ нижние границы интервалов

238. Задание <> ТЗ № 242

Для определения степени тесноты связи между качественными признаками используется

£ линейный коэффициент корреляции

R коэффициент контингенции

£ множественный коэффициент корреляции

239. Задание <> ТЗ № 243

В теории статистики различают в зависимости от числа группировочных признаков следующие виды группировок

240. Задание <> ТЗ № 244

Сущность метода условно-натурального измерения заключается в том, что натуральные единицы пересчитываются в условно-натуральные путем выражения разновидностей явления в

R единицах какого-либо эталона

241. Задание <> ТЗ № 245

Связь является функциональной, если определенному значению факторного признака соответствует

£ 0 значений результативного признака

£ 2 значения результативного признака

R строго определенное значение результативного признака

£ несколько значений результативного признака

242. Задание <> ТЗ № 249

По направлению связи в статистике классифицируются на

£ сильные и слабые

£ линейные и нелинейные

R прямые и обратные

£ закономерные и произвольные

243. Задание <> ТЗ № 252

Для трех предприятий с балансовой прибылью: первое предприятие с прибылью 10 млн. руб.; второе предприятие с прибылью 12 млн. руб.; третье предприятие с прибылью 10 млн. руб. ранги соответственно равны:

£ 1 ранг — первое предприятие; 2 ранг — второе предприятие; 3 ранг — третье предприятие

£ 1 ранг — второе предприятие; 2 ранг — первое предприятие; 3 ранг — третье предприятие

£ 1 ранг — третье предприятие; 2 ранг — первое предприятие; 3 ранг — второе предприятие

R 1 ранг — второе предприятие; 2,5 ранг — первое предприятие; 2,5 ранг — третье предприятие

Видео:Парная регрессия: линейная зависимостьСкачать

Пример нахождения статистической значимости коэффициентов регрессии

Числитель в этой формуле может быть рассчитан через коэффициент детерминации и общую дисперсию признака-результата: .
Для параметра a критерий проверки гипотезы о незначимом отличии его от нуля имеет вид:
,
где — оценка параметра регрессии, полученная по наблюдаемым данным;
μ_a – стандартная ошибка параметра a.
Для линейного парного уравнения регрессии:
.
Для проверки гипотезы о незначимом отличии от нуля коэффициента линейной парной корреляции в генеральной совокупности используют следующий критерий:
, где r_yx — оценка коэффициента корреляции, полученная по наблюдаемым данным; m_r – стандартная ошибка коэффициента корреляции r_yx.
Для линейного парного уравнения регрессии:
.
В парной линейной регрессии между наблюдаемыми значениями критериев существует взаимосвязь: t ₍ _b ₌₀₎ = t ₍_r₌₀₎.

Пример №1 . Уравнение имеет вид y=ax+b
1. Параметры уравнения регрессии.
Средние значения

Коэффициент детерминации
R 2 = 0.73 2 = 0.54, т.е. в 54% случаев изменения х приводят к изменению y . Другими словами — точность подбора уравнения регрессии — средняя.

x	y	x 2	y 2	x ∙ y	y(x)	(y-y cp ) 2	(y-y(x)) 2	(x-x p ) 2
69	124	4761	15376	8556	128.48	491.36	20.11	367.36
83	133	6889	17689	11039	141.4	173.36	70.56	26.69
92	146	8464	21316	13432	149.7	0.03	13.71	14.69
97	153	9409	23409	14841	154.32	46.69	1.73	78.03
88	138	7744	19044	12144	146.01	66.69	64.21	0.03
93	159	8649	25281	14787	150.63	164.69	70.13	23.36
74	145	5476	21025	10730	133.1	1.36	141.68	200.69
79	152	6241	23104	12008	137.71	34.03	204.21	84.03
105	168	11025	28224	17640	161.7	476.69	39.74	283.36
99	154	9801	23716	15246	156.16	61.36	4.67	117.36
85	127	7225	16129	10795	143.25	367.36	263.91	10.03
94	155	8836	24025	14570	151.55	78.03	11.91	34.03
1058	1754	94520	258338	155788	1754	1961.67	906.57	1239.67

2. Оценка параметров уравнения регрессии
Значимость коэффициента корреляции

По таблице Стьюдента находим Tтабл
T_табл (n-m-1;a) = (10;0.05) = 1.812
Поскольку Tнабл > Tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициента корреляции статистически — значим.

Анализ точности определения оценок коэффициентов регрессии

S _a = 0.2704
Доверительные интервалы для зависимой переменной

Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X = 88,16
(128.06;163.97)
Проверка гипотез относительно коэффициентов линейного уравнения регрессии
1) t-статистика

Статистическая значимость коэффициента регрессии a подтверждается (3.41>1.812).

Статистическая значимость коэффициента регрессии b подтверждается (2.7>1.812).
Доверительный интервал для коэффициентов уравнения регрессии
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими (t_табл=1.812):
(a — t_табл·S _a; a + t_табл·S_a)
(0.4325;1.4126)
(b — t_табл·S _b; b + t_табл·S_b)
(21.3389;108.3164)
2) F-статистики

Fkp = 4.96
Поскольку F > Fkp, то коэффициент детерминации статистически значим.

Пример №2 . По территориям региона приводятся данные за 199Х г.;

Номер региона	Среднедушевой прожиточный минимум в день одного трудоспособного, руб., х	Среднедневная заработная плата, руб., у
1	78	133
2	82	148
3	87	134
4	79	154
5	89	162
6	106	195
7	67	139
8	88	158
9	73	152
10	87	162
11	76	159
12	115	173

Требуется:
1. Построить линейное уравнение парной регрессии у от х.
2. Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации.
3. Оценить статистическую значимость параметров регрессии и корреляции.
4. Выполнить прогноз заработной платы у при прогнозном значении среднедушевого прожиточного минимума х , составляющем 107% от среднего уровня.
5. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.

Решение находим с помощью калькулятора.
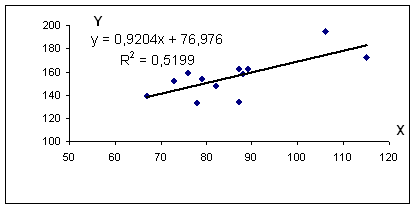
Использование графического метода .
Этот метод применяют для наглядного изображения формы связи между изучаемыми экономическими показателями. Для этого в прямоугольной системе координат строят график, по оси ординат откладывают индивидуальные значения результативного признака Y, а по оси абсцисс — индивидуальные значения факторного признака X.
Совокупность точек результативного и факторного признаков называется полем корреляции.
На основании поля корреляции можно выдвинуть гипотезу (для генеральной совокупности) о том, что связь между всеми возможными значениями X и Y носит линейный характер.
Линейное уравнение регрессии имеет вид y = bx + a + ε
Здесь ε — случайная ошибка (отклонение, возмущение).
Причины существования случайной ошибки:
1. Невключение в регрессионную модель значимых объясняющих переменных;
2. Агрегирование переменных. Например, функция суммарного потребления – это попытка общего выражения совокупности решений отдельных индивидов о расходах. Это лишь аппроксимация отдельных соотношений, которые имеют разные параметры.
3. Неправильное описание структуры модели;
4. Неправильная функциональная спецификация;
5. Ошибки измерения.
Так как отклонения ε_i для каждого конкретного наблюдения i – случайны и их значения в выборке неизвестны, то:
1) по наблюдениям x_i и y_i можно получить только оценки параметров α и β
2) Оценками параметров α и β регрессионной модели являются соответственно величины а и b, которые носят случайный характер, т.к. соответствуют случайной выборке;
Тогда оценочное уравнение регрессии (построенное по выборочным данным) будет иметь вид y = bx + a + ε, где e_i – наблюдаемые значения (оценки) ошибок ε_i, а и b соответственно оценки параметров α и β регрессионной модели, которые следует найти.
Для оценки параметров α и β — используют МНК (метод наименьших квадратов).
Система нормальных уравнений.
Для наших данных система уравнений имеет вид
12a+1027b=1869
1027a+89907b=161808
Из первого уравнения выражаем а и подставим во второе уравнение. Получаем b = 0.92, a = 76.98
Уравнение регрессии: y = 0.92 x + 76.98

1. Параметры уравнения регрессии.
Выборочные средние.

Коэффициент корреляции
Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:

Линейный коэффициент корреляции принимает значения от –1 до +1.
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 0 – прямая связь, иначе — обратная). В нашем примере связь прямая.
Коэффициент эластичности.
Коэффициенты регрессии (в примере b) нежелательно использовать для непосредственной оценки влияния факторов на результативный признак в том случае, если существует различие единиц измерения результативного показателя у и факторного признака х.
Для этих целей вычисляются коэффициенты эластичности и бета — коэффициенты. Коэффициент эластичности находится по формуле:

Он показывает, на сколько процентов в среднем изменяется результативный признак у при изменении факторного признака х на 1%. Он не учитывает степень колеблемости факторов.
Коэффициент эластичности меньше 1. Следовательно, при изменении среднедушевого прожиточного минимума в день на 1%, среднедневная заработная плата изменится менее чем на 1%. Другими словами — влияние среднедушевого прожиточного минимума Х на среднедневную заработную плату Y не существенно.
Бета – коэффициент показывает, на какую часть величины своего среднего квадратичного отклонения изменится в среднем значение результативного признака при изменении факторного признака на величину его среднеквадратического отклонения при фиксированном на постоянном уровне значении остальных независимых переменных:

Т.е. увеличение x на величину среднеквадратического отклонения этого показателя приведет к увеличению средней среднедневной заработной платы Y на 0.721 среднеквадратичного отклонения этого показателя.
1.4. Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации.

Поскольку ошибка меньше 15%, то данное уравнение можно использовать в качестве регрессии.
Коэффициент детерминации.
Квадрат (множественного) коэффициента корреляции называется коэффициентом детерминации, который показывает долю вариации результативного признака, объясненную вариацией факторного признака.
Чаще всего, давая интерпретацию коэффициента детерминации, его выражают в процентах.
R 2 = 0.72 2 = 0.5199, т.е. в 51.99 % случаев изменения среднедушевого прожиточного минимума х приводят к изменению среднедневной заработной платы y. Другими словами — точность подбора уравнения регрессии — средняя. Остальные 48.01% изменения среднедневной заработной платы Y объясняются факторами, не учтенными в модели.

x	y	x 2	y 2	x·y	y(x)	(y i — y ) 2	(y-y(x)) 2	(x i — x ) 2	\|y-y x \|:y
78	133	6084	17689	10374	148,77	517,56	248,7	57,51	0,1186
82	148	6724	21904	12136	152,45	60,06	19,82	12,84	0,0301
87	134	7569	17956	11658	157,05	473,06	531,48	2,01	0,172
79	154	6241	23716	12166	149,69	3,06	18,57	43,34	0,028
89	162	7921	26244	14418	158,89	39,06	9,64	11,67	0,0192
106	195	11236	38025	20670	174,54	1540,56	418,52	416,84	0,1049
67	139	4489	19321	9313	138,65	280,56	0,1258	345,34	0,0026
88	158	7744	24964	13904	157,97	5,06	0,0007	5,84	0,0002
73	152	5329	23104	11096	144,17	14,06	61,34	158,34	0,0515
87	162	7569	26244	14094	157,05	39,06	24,46	2,01	0,0305
76	159	5776	25281	12084	146,93	10,56	145,7	91,84	0,0759
115	173	13225	29929	19895	182,83	297,56	96,55	865,34	0,0568
1027	1869	89907	294377	161808	1869	3280,25	1574,92	2012,92	0,6902

2. Оценка параметров уравнения регрессии.
2.1. Значимость коэффициента корреляции.

По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=10 находим t_крит:
t_крит = (10;0.05) = 1.812
где m = 1 — количество объясняющих переменных.
Если t_набл > t_критич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку t_набл > t_крит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически — значим.
В парной линейной регрессии t 2 _r = t 2 _b и тогда проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.

2.3. Анализ точности определения оценок коэффициентов регрессии.
Несмещенной оценкой дисперсии возмущений является величина:

S 2 _y = 157.4922 — необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии).

12.5496 — стандартная ошибка оценки (стандартная ошибка регрессии).
S _a — стандартное отклонение случайной величины a.

S_b — стандартное отклонение случайной величины b.

2.4. Доверительные интервалы для зависимой переменной.
Экономическое прогнозирование на основе построенной модели предполагает, что сохраняются ранее существовавшие взаимосвязи переменных и на период упреждения.
Для прогнозирования зависимой переменной результативного признака необходимо знать прогнозные значения всех входящих в модель факторов.
Прогнозные значения факторов подставляют в модель и получают точечные прогнозные оценки изучаемого показателя.
(a + bx_p ± ε)
где
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X _p = 94

(76.98 + 0.92*94 ± 7.8288)
(155.67;171.33)
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.
2.5. Проверка гипотез относительно коэффициентов линейного уравнения регрессии.
1) t-статистика. Критерий Стьюдента.
Проверим гипотезу H₀ о равенстве отдельных коэффициентов регрессии нулю (при альтернативе H₁ не равно) на уровне значимости α=0.05.
t_крит = (10;0.05) = 1.812

Поскольку 3.2906 > 1.812, то статистическая значимость коэффициента регрессии b подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).

Поскольку 3.1793 > 1.812, то статистическая значимость коэффициента регрессии a подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Доверительный интервал для коэффициентов уравнения регрессии.
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:
(b — t_крит S_b; b + t_крит S_b)
(0.9204 — 1.812·0.2797; 0.9204 + 1.812·0.2797)
(0.4136;1.4273)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
(a-t_a)
(76.9765 — 1.812·24.2116; 76.9765 + 1.812·24.2116)
(33.1051;120.8478)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
2) F-статистики. Критерий Фишера.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с k1=(m) и k2=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.

где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H₀: R 2 =0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:

где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=10, Fkp = 4.96
Поскольку фактическое значение F > Fkp, то коэффициент детерминации статистически значим (Найденная оценка уравнения регрессии статистически надежна).

Видео:Эконометрика. Оценка значимости параметров уравнения регрессии. Критерий Стьюдента.Скачать

Задача №1 Построение уравнения регрессии

Имеются следующие данные разных стран об индексе розничных цен на продукты питания (х) и об индексе промышленного производства (у).

Индекс розничных цен на продукты питания (х)	Индекс промышленного производства (у)
1	100	70
2	105	79
3	108	85
4	113	84
5	118	85
6	118	85
7	110	96
8	115	99
9	119	100
10	118	98
11	120	99
12	124	102
13	129	105
14	132	112

Требуется:

1. Для характеристики зависимости у от х рассчитать параметры следующих функций:

В) равносторонней гиперболы.

2. Для каждой модели рассчитать показатели: тесноты связи и среднюю ошибку аппроксимации.

3. Оценить статистическую значимость параметров регрессии и корреляции.

4. Выполнить прогноз значения индекса промышленного производства у при прогнозном значении индекса розничных цен на продукты питания х=138.

Решение:

1. Для расчёта параметров линейной регрессии

Решаем систему нормальных уравнений относительно a и b:

Построим таблицу расчётных данных, как показано в таблице 1.

Таблица 1 Расчетные данные для оценки линейной регрессии

№ п/п	х	у	ху	x 2	y 2
1	100	70	7000	10000	4900	74,26340	0,060906
2	105	79	8295	11025	6241	79,92527	0,011712
3	108	85	9180	11664	7225	83,32238	0,019737
4	113	84	9492	12769	7056	88,98425	0,059336
5	118	85	10030	13924	7225	94,64611	0,113484
6	118	85	10030	13924	7225	94,64611	0,113484
7	110	96	10560	12100	9216	85,58713	0,108467
8	115	99	11385	13225	9801	91,24900	0,078293
9	119	100	11900	14161	10000	95,77849	0,042215
10	118	98	11564	13924	9604	94,64611	0,034223
11	120	99	11880	14400	9801	96,91086	0,021102
12	124	102	12648	15376	10404	101,4404	0,005487
13	129	105	13545	16641	11025	107,1022	0,020021
14	132	112	14784	17424	12544	110,4993	0,013399
Итого:	1629	1299	152293	190557	122267	1299,001	0,701866
Среднее значение:	116,3571	92,78571	10878,07	13611,21	8733,357	х	х
	8,4988	11,1431	х	х	х	х	х
	72,23	124,17	х	х	х	х	х

Среднее значение определим по формуле:

Cреднее квадратическое отклонение рассчитаем по формуле:

и занесём полученный результат в таблицу 1.

Возведя в квадрат полученное значение получим дисперсию:

Параметры уравнения можно определить также и по формулам:

Таким образом, уравнение регрессии:

Следовательно, с увеличением индекса розничных цен на продукты питания на 1, индекс промышленного производства увеличивается в среднем на 1,13.

Рассчитаем линейный коэффициент парной корреляции:

Связь прямая, достаточно тесная.

Определим коэффициент детерминации:

Вариация результата на 74,59% объясняется вариацией фактора х.

Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчётные) значения .

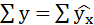
следовательно, параметры уравнения определены правильно.

Рассчитаем среднюю ошибку аппроксимации – среднее отклонение расчётных значений от фактических:

В среднем расчётные значения отклоняются от фактических на 5,01%.

Оценку качества уравнения регрессии проведём с помощью F-теста.

F-тест состоит в проверке гипотезы Н₀ о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического F_факт и критического (табличного) F_табл значений F-критерия Фишера.

F_факт определяется по формуле:

где n – число единиц совокупности;

m – число параметров при переменных х.

Таким образом, Н₀ – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.

Полученные оценки уравнения регрессии позволяют использовать его для прогноза.

Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:

2. Степенная регрессия имеет вид:

Для определения параметров производят логарифмирование степенной функции:

Для определения параметров логарифмической функции строят систему нормальных уравнений по способу наименьших квадратов:

Построим таблицу расчётных данных, как показано в таблице 2.

Таблица 2 Расчетные данные для оценки степенной регрессии

№п/п	х	у	lg x	lg y	lg x*lg y	(lg x) 2	(lg y) 2
1	100	70	2,000000	1,845098	3,690196	4,000000	3,404387
2	105	79	2,021189	1,897627	3,835464	4,085206	3,600989
3	108	85	2,033424	1,929419	3,923326	4,134812	3,722657
4	113	84	2,053078	1,924279	3,950696	4,215131	3,702851
5	118	85	2,071882	1,929419	3,997528	4,292695	3,722657
6	118	85	2,071882	1,929419	3,997528	4,292695	3,722657
7	110	96	2,041393	1,982271	4,046594	4,167284	3,929399
8	115	99	2,060698	1,995635	4,112401	4,246476	3,982560
9	119	100	2,075547	2,000000	4,151094	4,307895	4,000000
10	118	98	2,071882	1,991226	4,125585	4,292695	3,964981
11	120	99	2,079181	1,995635	4,149287	4,322995	3,982560
12	124	102	2,093422	2,008600	4,204847	4,382414	4,034475
13	129	105	2,110590	2,021189	4,265901	4,454589	4,085206
14	132	112	2,120574	2,049218	4,345518	4,496834	4,199295
Итого	1629	1299	28,90474	27,49904	56,79597	59,69172	54,05467
Среднее значение	116,3571	92,78571	2,064624	1,964217	4,056855	4,263694	3,861048
	8,4988	11,1431	0,031945	0,053853	х	х	х
	72,23	124,17	0,001021	0,0029	х	х	х

Продолжение таблицы 2 Расчетные данные для оценки степенной регрессии

№п/п	х	у
1	100	70	74,16448	17,34292	0,059493	519,1886
2	105	79	79,62057	0,385112	0,007855	190,0458
3	108	85	82,95180	4,195133	0,024096	60,61728
4	113	84	88,59768	21,13866	0,054734	77,1887
5	118	85	94,35840	87,57961	0,110099	60,61728
6	118	85	94,35840	87,57961	0,110099	60,61728
7	110	96	85,19619	116,7223	0,11254	10,33166
8	115	99	90,88834	65,79901	0,081936	38,6174
9	119	100	95,52408	20,03384	0,044759	52,04598
10	118	98	94,35840	13,26127	0,037159	27,18882
11	120	99	96,69423	5,316563	0,023291	38,6174
12	124	102	101,4191	0,337467	0,005695	84,90314
13	129	105	107,4232	5,872099	0,023078	149,1889
14	132	112	111,0772	0,85163	0,00824	369,1889
Итого	1629	1299	1296,632	446,4152	0,703074	1738,357
Среднее значение	116,3571	92,78571	х	х	х	х
	8,4988	11,1431	х	х	х	х
	72,23	124,17	х	х	х	х

Решая систему нормальных уравнений, определяем параметры логарифмической функции.

Получим линейное уравнение:

Выполнив его потенцирование, получим:

Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата 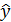. По ним рассчитаем показатели: тесноты связи – индекс корреляции и среднюю ошибку аппроксимации.

Связь достаточно тесная.

В среднем расчётные значения отклоняются от фактических на 5,02%.

Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:

3. Уравнение равносторонней гиперболы

Для определения параметров этого уравнения используется система нормальных уравнений:

Произведем замену переменных

и получим следующую систему нормальных уравнений:

Решая систему нормальных уравнений, определяем параметры гиперболы.

Составим таблицу расчётных данных, как показано в таблице 3.

Таблица 3 Расчетные данные для оценки гиперболической зависимости

№п/п	х	у	z	yz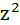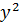
1	100	70	0,010000000	0,700000	0,0001000	4900
2	105	79	0,009523810	0,752381	0,0000907	6241
3	108	85	0,009259259	0,787037	0,0000857	7225
4	113	84	0,008849558	0,743363	0,0000783	7056
5	118	85	0,008474576	0,720339	0,0000718	7225
6	118	85	0,008474576	0,720339	0,0000718	7225
7	110	96	0,009090909	0,872727	0,0000826	9216
8	115	99	0,008695652	0,860870	0,0000756	9801
9	119	100	0,008403361	0,840336	0,0000706	10000
10	118	98	0,008474576	0,830508	0,0000718	9604
11	120	99	0,008333333	0,825000	0,0000694	9801
12	124	102	0,008064516	0,822581	0,0000650	10404
13	129	105	0,007751938	0,813953	0,0000601	11025
14	132	112	0,007575758	0,848485	0,0000574	12544
Итого:	1629	1299	0,120971823	11,13792	0,0010510	122267
Среднее значение:	116,3571	92,78571	0,008640844	0,795566	0,0000751	8733,357
	8,4988	11,1431	0,000640820	х	х	х
	72,23	124,17	0,000000411	х	х	х

Продолжение таблицы 3 Расчетные данные для оценки гиперболической зависимости

№п/п	х	у
1	100	70	72,3262	0,033231	5,411206	519,1886
2	105	79	79,49405	0,006254	0,244083	190,0458
3	108	85	83,47619	0,017927	2,322012	60,61728
4	113	84	89,64321	0,067181	31,84585	77,1887
5	118	85	95,28761	0,121031	105,8349	60,61728
6	118	85	95,28761	0,121031	105,8349	60,61728
7	110	96	86,01027	0,10406	99,79465	10,33166
8	115	99	91,95987	0,071112	49,56344	38,6174
9	119	100	96,35957	0,036404	13,25272	52,04598
10	118	98	95,28761	0,027677	7,357059	27,18882
11	120	99	97,41367	0,016024	2,516453	38,6174
12	124	102	101,46	0,005294	0,291565	84,90314
13	129	105	106,1651	0,011096	1,357478	149,1889
14	132	112	108,8171	0,028419	10,1311	369,1889
Итого:	1629	1299	1298,988	0,666742	435,7575	1738,357
Среднее значение:	116,3571	92,78571	х	х	х	х
	8,4988	11,1431	х	х	х	х
	72,23	124,17	х	х	х	х

Значения параметров регрессии a и b составили:

Связь достаточно тесная.

В среднем расчётные значения отклоняются от фактических на 4,76%.

По уравнению равносторонней гиперболы получена наибольшая оценка тесноты связи по сравнению с линейной и степенной регрессиями. Средняя ошибка аппроксимации остаётся на допустимом уровне.