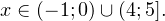Полный перечень схем равносильных преобразований, которые облегчают решение логарифмических неравенств.
Пусть $$ fleft( x right) = f $$, $$ gleft( x right) = g $$ — функции, $$ a,;b,;c $$ — действительные числа.
1. $$ log _a f vee 0 Leftrightarrow left( right)left( right) vee 0$$, ОДЗ: $$ left< begin f > 0; \ a > 0,<rm>a ne 1. \ end right.$$
2. $$ log _a f vee b Leftrightarrow left( right)left( right) vee 0 $$, ОДЗ: $$ left< begin f > 0; \ a > 0,<rm>a ne 1. \ end right.$$
3. $$ log _a f vee log _a g Leftrightarrow left( right)left( right) vee 0 $$, ОДЗ: $$ left< begin f > 0,<rm>g > 0; \ a > 0,<rm>a ne 1. \ end right. $$
4. $$ log _a f vee log _c f Leftrightarrow left( right)left( right)left( right)left( right) vee $$, ОДЗ: $$ left< begin f > 0; \ a > 0,<rm>a ne 1; \ c > 0,<rm>c ne 1. \ end right. $$
5. $$ left( right) vee 0 Leftrightarrow left( right)left( right) vee 0] $$, ОДЗ: $$ left< begin f > 0,<rm>g > 0; \ a > 0,<rm>a ne 1. \ end right. $$
6. $$ log _a f cdot log _c g vee 0 Leftrightarrow left( right)left( right)left( right)left( right) vee 0 $$, ОДЗ: $$ left< begin f > 0,<rm>g > 0; \ a > 0,<rm>a ne 1; \ c > 0,<rm>c ne 1. \ end right. $$
Замечание. Если в этих схемах $$ a,;b,;c$$ (действительные числа) заменить элементарными функциями, то получаться схемы равносильных преобразований логарифмических неравенств, содержащих в основании неизвестную величину.
- Логарифмические уравнения и неравенства
- Логарифмическая функция
- Определение
- Основные свойства
- Решение логарифмических уравнений и неравенств
- конспект урока «Равносильность уравнений (Логарифмические уравнения)» план-конспект урока по алгебре (11 класс) по теме
- Скачать:
- Предварительный просмотр:
- Предварительный просмотр:
- Подписи к слайдам:
- 🎥 Видео
Видео:Логарифмические уравнения. 11 класс.Скачать

Логарифмические уравнения и неравенства
Логарифмическим уравнениям и неравенствам в вариантах ЕГЭ по математике посвящена задача C3. Научиться решать задания C3 из ЕГЭ по математике должен каждый ученик, если он хочет сдать предстоящий экзамен на «хорошо» или «отлично». В данной статье представлен краткий обзор часто встречающихся логарифмических уравнений и неравенств, а также основных методов их решения.
Итак, разберем сегодня несколько примеров логарифмических уравнений и неравенств, которые предлагались учащимся в вариантах ЕГЭ по математике прошлых лет. Но начнет с краткого изложение основных теоретических моментов, которые нам понадобятся для их решения.
Видео:11 класс, 17 урок, Логарифмические уравненияСкачать

Логарифмическая функция
Определение
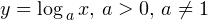
называют логарифмической функцией.
Основные свойства
Основные свойства логарифмической функции y = loga x:
| | a > 1 | 0 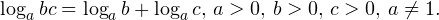 0,, b>0,, c>0,, ane 1. ]» title=»Rendered by QuickLaTeX.com»/> 0,, b>0,, c>0,, ane 1. ]» title=»Rendered by QuickLaTeX.com»/>• Логарифм частного двух положительных чисел равен разности логарифмов этих чисел:
• Если a и b — положительные числа, причем a ≠ 1, то для любого числа r справедливо равенство:
• Если a, b, c — положительные числа, причем a и c отличны от единицы, то имеет место равенство (формула перехода к новому основанию логарифма):
Видео:Проще простого! Как решить Логарифмическое Уравнение?Скачать  Решение логарифмических уравнений и неравенствПример 1. Решите уравнение: Решение. В область допустимых значений входят только те x, при которых выражение, находящееся под знаком логарифма, больше нуля. Эти значения определяются следующей системой неравенств:
С учетом того, что получаем промежуток, определяющий область допустимых значений данного логарифмического уравнения: На основании теоремы 1, все условия которой здесь выполнены, переходим к следующему равносильному квадратичному уравнению: В область допустимых значений входит только первый корень. Ответ: x = 7. Пример 2. Решите уравнение: Решение. Область допустимых значений уравнения определяется системой неравенств:
Очевидно, что эти два условия противоречат друг другу. То есть нет ни одного такого значения x, при котором одновременно выполнялись бы оба неравенства. Область допустимых значений уравнения является пустым множеством, а значит решений у данного логарифмического уравнения нет. Ответ: корней нет. Обратите внимание, что в этом задании нам вообще не пришлось искать корни уравнения. Достаточно оказалось определить, что его область допустимых значений не содержит ни одного действительно числа. Это одно из преимуществ такой последовательности решения логарифмических уравнений и неравенств (начинать с определения области допустимых значений уравнения, а затем решать его путем равносильных преобразований). Примет 3. Решите уравнение: Решение. Область допустимых значений уравнения определяется здесь легко: x > 0. Уравнение принимает вид: Оба ответа входят в область допустимых значений уравнения, поскольку являются положительными числами. Пример 4. Решите уравнение: Решение. Вновь начнем решение с определения области допустимых значений уравнения. Она определяется следующей системой неравенств:
Воспользовавшись правилом сложения логарифмов, переходим к равносильному в области допустимых значений уравнению: Основания логарифмов одинаковы, поэтому в области допустимых значений можно перейти к следующему квадратному уравнению: Первый корень не входит в область допустимых значений уравнения, второй — входит. Ответ: x = -1. Пример 5. Решите уравнение: Решение. Будем искать решения в промежутке x > 0, x≠1. Преобразуем уравнение к равносильному: Оба ответа входят в область допустимых значений уравнения. Пример 6. Решите уравнение: Решение. Система неравенств, определяющая область допустимых значений уравнения, имеет на этот раз вид: Используя свойства логарифма, преобразуем уравнение к равносильному в области допустимых значений уравнению: Используя формулу перехода к новому основанию логарифма, получаем: В область допустимых значений входит только один ответ: x = 4. Перейдем теперь к логарифмическим неравенствам. Это как раз то, с чем вам придется иметь дело на ЕГЭ по математике. Для решения дальнейших примеров нам потребуется следующая теорема: Теорема 2. Если f(x) > 0 и g(x) > 0, то: Решение. Начнем с определения области допустимых значений неравенства. Выражение, стоящее под знаком логарифмической функции, должно принимать только положительные значения. Это значит, что искомая область допустимых значений определяется следующей системой неравенств:
Так как в основании логарифма стоит число, меньшее единицы, соответствующая логарифмическая функция будет убывающей, а потому равносильным по теореме 2 будет переход к следующему квадратичному неравенству: Окончательно, с учетом области допустимых значений получаем ответ: Пример 8. Решите неравенство: Решение. Вновь начнем с определения области допустимых значений:
На множестве допустимых значений неравенства проводим равносильные преобразования: После сокращения и перехода к равносильному по теореме 2 неравенству получаем: С учетом области допустимых значений получаем окончательный ответ: Пример 9. Решите логарифмическое неравенство: Решение. Область допустимых значений неравенства определяется следующей системой:
Видно, что в области допустимых значений выражение, стоящее в основании логарифма, всегда больше единицы, а потому равносильным по теореме 2 будет переход к следующему неравенству: С учетом области допустимых значений получаем окончательный ответ: Пример 10. Решите неравенство: Решение. Область допустимых значений неравенства определяется системой неравенств:
I способ. Воспользуемся формулой перехода к новому основанию логарифма и перейдем к равносильному в области допустимых значений неравенству: Неравенство будет равносильно двум системам. Первой: Итак, окончательный ответ: II способ. Решаем методом интервалов. Преобразуем неравенство к виду: Вычтем из знаменателя С учетом того, что выражения Множество решений данного неравенства Итак, Итак, что нужно для того, чтобы решать логарифмические уравнения и неравенства?
Главное же требование — это настойчивость в достижении своей цели. Учитесь, тренируйтесь, если нужно — ежедневно, изучайте и запоминайте на примерах основные способы решения неравенств и их систем, анализируйте возникающие ошибки и не допускайте их в будущем. За помощью в этом нелегком деле вы можете обратиться к своему школьному учителю по математике, репетитору, родителям, друзьям и знакомым, книгам, а также огромному количеству материалов, доступных на просторах Интернета. Желаю вам успехов в подготовке к Единому государственному экзамену по математике. Видео:Логарифмы с нуля за 20 МИНУТ! Introduction to logarithms.Скачать  конспект урока «Равносильность уравнений (Логарифмические уравнения)» |
| Вложение | Размер |
|---|---|
| konspekt_ravnosilnost_uravneniy._logarifmicheskie_uravneniya.docx | 128.98 КБ |
| ravnosilnost_uravneniy._logarifmicheskie_uravneniya.ppt | 616 КБ |
Видео:Круговорот воды в природе ➜ Решение логарифмических уравнений из ЕГЭ #ShortsСкачать

Предварительный просмотр:
Урок с использованием ИКТ в рамках подготовки к ЕГЭ по математике.
Тема: Равносильность уравнений. (Логарифмические уравнения) 11 класс.
- продолжить изучение способов решения логарифмических уравнений, уделяя внимание этапам решения, характеристики преобразований, приводящих к нахождению корней;
- развивать логическое мышление через приемы сравнения, умение классифицировать, акцентировать внимание на постановку вопроса в задании;
- воспитывать ответственное отношение к учебному труду, дать рекомендации школьникам, собирающимся сдавать ЕГЭ.
компьютер, экран, обучающе — демонстрационная программа «Логарифмические уравнения».
I. Организационный момент. (перед началом урока для работы в группах разделить детей по 5-6 человек, а в начале урока учащиеся садятся за компьютеры,).
— Сегодняшний урок я хотела начать с вопроса: Бывает ли верно равенство 2=3? (заслушать высказывания учеников)
— На прошлом уроке я попросила вас написать свой вес на листочках, просмотрев их, я пришла к выводу, что в наше время 2 мальчика имеют тот же вес, что и 3 девочки…
— И в математике, оказывается можно встретить такое. Об этом вам расскажет_______________. (ученик подготовил «доказательство»).
«Доказать» это «равенство» можно следующим образом:
2 ,
(Ответ: ошибка заключается в неравносильном преобразовании при извлечении квадратного корня:
— Тема нашего урока «Равносильность уравнений» и сегодня мы рассмотрим только решение логарифмических уравнений и их преобразования, которые могут привести к неверному решению.
II. Актуализация знаний.
— Но сначала посмотрим, достаточно хорошо вы знаете определение логарифма и его свойства. Для этого предлагаю выполнить тест. (У каждого ученика бланк для ответов типа бланка для сдачи ЕГЭ, на выполнение отводится 3-5 мин. Проверку провести с помощью презентации.)
При выполнении заданий А1 – А5 в бланке ответов №1 под номером выполняемого задания поставьте знак » » в клеточке, номер которой соответствует номеру выбранного вами ответа.
А1. Найдите значение выражения
1) 5 2) 3 7 3) 3 4)
1) 0 2) — 1 3) 1 4) 5
А3. Укажите значение выражения
1) 1 2) 3 3) 2 4) 24
А4. Найдите область определения функции .
А5. Укажите промежуток, содержащий корень уравнения
1) (0;5) 2) (5;15) 3) (15;25) 4) (25;100)
При выполнении заданий А1 – А5 в бланке ответов №1 под номером выполняемого задания поставьте знак «» в клеточке, номер которой соответствует номеру выбранного вами ответа.
А1. Найдите значение выражения .
1) 1 2) 2 3) — 1 4) — 2
А3. Укажите значение выражения
А4. Найдите область определения функции .
А5. Укажите промежуток, содержащий корень уравнения
1) (1;30) 2) (30;50) 3) (50;100) 4) (100;200)
(после выполнения теста произвести проверку с помощью слайда презентации: вариант I: слайд 2, вариант II: слайд 3)
III. Систематизация теоретического материала.
— Итак, мы повторили определение и свойства логарифма. А теперь дайте определение равносильных уравнений, уравнения — следствия. Чем отличаются эти определения? Опишите схему решения любого уравнения. (технический этап, анализ решения, проверка) Совпадает ли множество корней последнего уравнения с множеством корней исходного уравнения?
Задание 1. ( слайд 4 )
— Можно ли сказать, что эти уравнения равносильны?
Что произошло с одним из корней первого уравнения?
Что можно сказать об области определения левой и правой частей свойств логарифмов ? ( слайд 5)
Задание 2. Решить уравнение (на сужение ОДЗ)
Задание 3. Решить уравнение
Какие преобразования в рассмотренных уравнениях приводят к потере корней?
— деление на выражение с переменной,
— формальное применение логарифмических формул.
Известны ли вам другие преобразования, приводящие к сужению ОДЗ?
— логарифмирование обеих частей уравнения,
— извлечение корня чётной степени.
Назовите преобразования, приводящие к расширению ОДЗ, появлению посторонних корней?
— освобождение от знаменателя, содержащего переменную величину,
— освобождение от знаков корней чётной степени,
Перечислите теоремы равносильности, которые гарантируют равносильность преобразований без дополнительных условий.
— перенос членов уравнения…,
— возведение в нечётную степень,
IV. Физминутка. (предложить группам сесть за столы)
Задание 4. (Работа в группах) Представьте, что решая некоторое уравнение, вы на каком-то шаге переходите от уравнения (1) к уравнению (2). Что произошло с корнями уравнения (1) при этом переходе?
Поставьте в колонке I знак «+», если при переходе от (1) к (2) ни один из корней (1) не потерялся, знак « — » — если потерялся;
в колонке II знак «+», если при переходе от (1) к (2) не появилось новых корней, знак « — » — если они появились;
в колонке III знак «+», если уравнения (1) и (2) равносильны, знак « — » — в противном случае.
IV. Решение заданий части С.
Задание 5. Решить уравнение
Решение. Можно заметить, что корень уравнения 1. Докажем, что других корней нет. Функция убывает на своей области определения, т.к. она является композицией убывающей линейной и возрастающей логарифмической функций. Функция возрастает на . Следовательно, графики этих функций могут иметь не более одной точки пересечения. Абсцисса этой точки уже найдена. Получаем, что единственным корнем уравнения является х=1.
VI. Рефлексия. (Проверь своё внимание!). (слайд 10)
Логарифмическая «комедия 2>3». ( слайд 11 )
верно? (бесспорно правильно.)
— запишем в виде степени числа .
верно? (не внушает сомнения)
— прологарифмируем обе части по основанию 10:
2lg 3 lg
— сократив на lg имеем 2
— В чём ошибка этого доказательства? (при сокращении на lg необходимо изменить знак неравенства, т.к. lg
VI. Итог урока.
— Наш урок заканчивается. Что на нем было самым главным? Что узнали нового?
1. Найдите ОДЗ уравнения
Пустое множество. Т.к. система, определяющая ОДЗ, не имеет решений.
Решение. Сумма двух неотрицательных выражений равна нулю тогда и только тогда, когда каждое из них равно нулю. Поэтому…
Корни первого уравнения числа -1 и 2. Решения системы содержатся среди этих чисел, поэтому достаточно проверить, являются ли они корнями второго уравнения. Подстановка показывает, что корнем второго уравнения яв. число -1.
Предварительный просмотр:
Видео:11 класс, 26 урок, Равносильность уравненийСкачать

Подписи к слайдам:
Логарифмические уравнения МБОУ «Гимназия №1» с. Красногвардейское Равносильность уравнений.
Ответы к заданиям с выбором ответа А1. Найдите значение выражения 1) 5 2) 3 7 3) 3 4) А2. Вычислите 1) 0 2) — 1 3) 1 4) 5 А3. Укажите значение выражения 1) 1 2) 3 3) 2 4) 24 А4. Найдите область определения функции 1) 2) 3) 4) А5. Укажите промежуток, содержащий корень уравнения 1) (0;5) 2) (5;15) 3) (15;25) 4) (25;100) Вариант 1
Ответы к заданиям с выбором ответа А1. Найдите значение выражения 1) 10 2) 5 3) 4) 20 А2. Вычислите 1) 1 2) 2 3) — 1 4) — 2 А3. Укажите значение выражения 1) 2) 3) 3,5 4) 4 А4. Найдите область определения функции 1) 2) 3) 4) А5. Укажите промежуток, содержащий корень уравнения 1) (1;30) 2) (30;50) 3) (50;100) 4) (100;200) Вариант 2
Преобразование, приводящее к потере корней уравнения. Преобразование, не приводящее к потере корней уравнения. log 2 log log х=16. log 2 log log х=16 или х = — 16. Задание 1.
Решить уравнение Решение. используя свойство логарифмов получим: или Первая система решений не имеет, решение второй системы: X=1. Ответ: 1. По определению логарифма Задание 2.
Задание 3. Решит е уравнение Решение. Преобразуем уравнение с помощью свойств логарифма, учитывая, что В ответе запишите число корней уравнения. Перенесём все члены уравнения в левую часть и разложим на множители: Корнями этого уравнения являются числа 1; 0,2 и 0,04. С учётом области определения получаем ,что корнями уравнения являются числа 0,2 и 0,04. Ответ: 2.
Задание 4. Представьте, что решая некоторое уравнение, вы на каком-то шаге переходите от уравнения (1) к уравнению (2). Что произошло с корнями уравнения (1) при этом переходе? Поставьте в колонке I знак «+», если при переходе от (1) к (2) ни один из корней (1) не потерялся, знак « — » — если потерялся; в колонке II знак «+», если при переходе от (1) к (2) не появилось новых корней, знак « — » — если они появились; в колонке III знак «+», если уравнения (1) и (2) равносильны, знак « — » — в противном случае.
(1) (2) I II III 1. + + + 2. + — — 3. + + + 4. + — — 5. — + — 6. + — — 7. + + + 8. — + — Ответы
Проверь своё внимание! 1) 2 ) 4 ) 5 ) 3 )
Логарифмическая «комедия 2>3». верно ? , lg lg 2 lg 3 lg 2 > 3. 2 Мне нравится
🎥 Видео
Умножаем логарифмы В УМЕ🧠Скачать

84 людей этого не знают! Секретный способ решения Логарифмических УравненийСкачать

✓ Как решать логарифмические уравнения и неравенства, не помня свойства логарифмов | Борис ТрушинСкачать

Интересная задача на логарифмы в ЕГЭСкачать

Решение логарифмических уравнений. Вебинар | МатематикаСкачать

Логарифмические уравнения 🥷🏿Скачать

Шпаргалка для школьника — Все Свойства Логарифмов за 15 минутСкачать

Решение логарифмических уравненийСкачать

ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯСкачать

решение логарифмических уравненийСкачать

Учимся решать сложные логарифмические уравненияСкачать

§19 Логарифмические уравненияСкачать

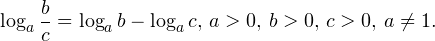 0,, b>0,, c>0,, ane 1. ]» title=»Rendered by QuickLaTeX.com»/>
0,, b>0,, c>0,, ane 1. ]» title=»Rendered by QuickLaTeX.com»/>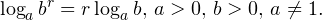 0,, b>0,, ane 1. ]» title=»Rendered by QuickLaTeX.com»/>
0,, b>0,, ane 1. ]» title=»Rendered by QuickLaTeX.com»/>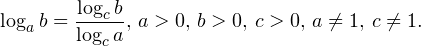 0,, b>0,, c>0,, ane 1,, cne 1. ]» title=»Rendered by QuickLaTeX.com»/>
0,, b>0,, c>0,, ane 1,, cne 1. ]» title=»Rendered by QuickLaTeX.com»/>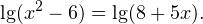
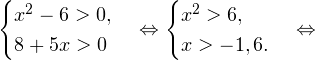 0, \ 8+5x > 0 end Leftrightarrow begin x^2 > 6, \ x>-1,6. end Leftrightarrow ]» title=»Rendered by QuickLaTeX.com»/>
0, \ 8+5x > 0 end Leftrightarrow begin x^2 > 6, \ x>-1,6. end Leftrightarrow ]» title=»Rendered by QuickLaTeX.com»/>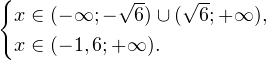
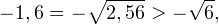 -sqrt, ]» title=»Rendered by QuickLaTeX.com»/>
-sqrt, ]» title=»Rendered by QuickLaTeX.com»/>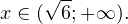
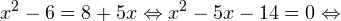
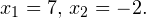
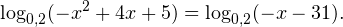
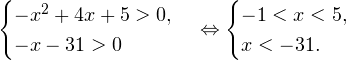 0, \ -x-31>0 endLeftrightarrow begin -1
0, \ -x-31>0 endLeftrightarrow begin -1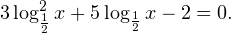
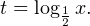
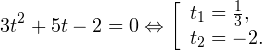
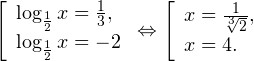
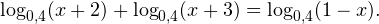
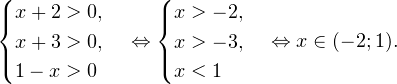 0, \ x+3>0, \ 1-x>0 endLeftrightarrow begin x>-2, \ x>-3, \ x
0, \ x+3>0, \ 1-x>0 endLeftrightarrow begin x>-2, \ x>-3, \ x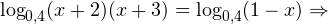
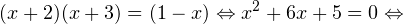
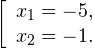
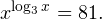
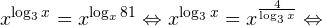
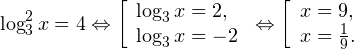
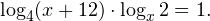
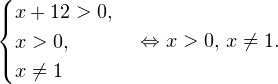 0, \ x>0, \ xne 1 endLeftrightarrow x>0,, xne 1. ]» title=»Rendered by QuickLaTeX.com»/>
0, \ x>0, \ xne 1 endLeftrightarrow x>0,, xne 1. ]» title=»Rendered by QuickLaTeX.com»/>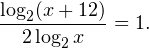
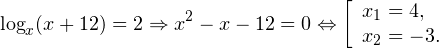
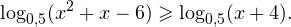
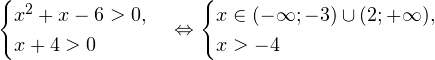 0, \ x+4>0 endLeftrightarrow begin xin(-mathcal;-3)cup(2;+mathcal), \ x>-4 end ]» title=»Rendered by QuickLaTeX.com»/>
0, \ x+4>0 endLeftrightarrow begin xin(-mathcal;-3)cup(2;+mathcal), \ x>-4 end ]» title=»Rendered by QuickLaTeX.com»/>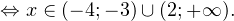
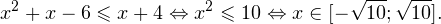
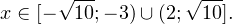
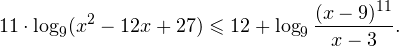
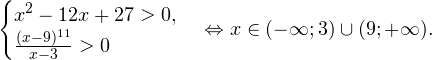 0, \ frac<(x-9)^>>0 endLeftrightarrow xin(-mathcal;3)cup(9;+mathcal). ]» title=»Rendered by QuickLaTeX.com»/>
0, \ frac<(x-9)^>>0 endLeftrightarrow xin(-mathcal;3)cup(9;+mathcal). ]» title=»Rendered by QuickLaTeX.com»/>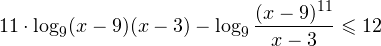
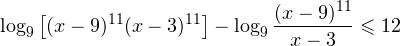
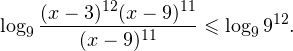
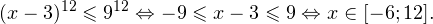
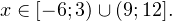
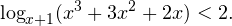
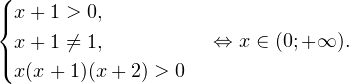 0, \ x+1ne 1,\ x(x+1)(x+2)>0 endLeftrightarrow xin (0;+mathcal). ]» title=»Rendered by QuickLaTeX.com»/>
0, \ x+1ne 1,\ x(x+1)(x+2)>0 endLeftrightarrow xin (0;+mathcal). ]» title=»Rendered by QuickLaTeX.com»/>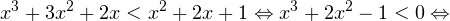
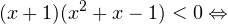
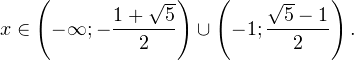
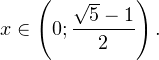
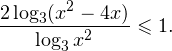
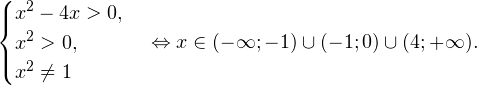 0, \ x^2>0, \ x^2ne 1 endLeftrightarrow xin(-mathcal;-1)cup(-1;0)cup(4;+mathcal). ]» title=»Rendered by QuickLaTeX.com»/>
0, \ x^2>0, \ x^2ne 1 endLeftrightarrow xin(-mathcal;-1)cup(-1;0)cup(4;+mathcal). ]» title=»Rendered by QuickLaTeX.com»/>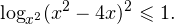
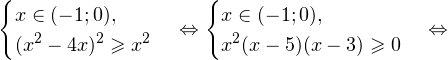
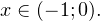
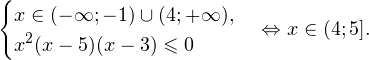
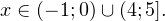
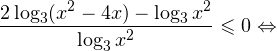
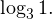 Это ничего не изменит, поскольку
Это ничего не изменит, поскольку 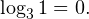
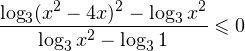
 и
и  — одного знака при
— одного знака при 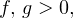 0,» title=»Rendered by QuickLaTeX.com» height=»18″ width=»74″ style=»vertical-align: -4px;»/> в области допустимых значений имеет место следующий равносильный переход:
0,» title=»Rendered by QuickLaTeX.com» height=»18″ width=»74″ style=»vertical-align: -4px;»/> в области допустимых значений имеет место следующий равносильный переход: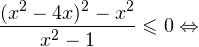
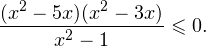
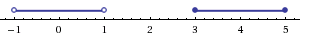
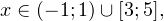 а с учетом области допустимых значений получаем тот же результат:
а с учетом области допустимых значений получаем тот же результат: