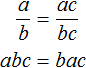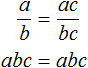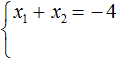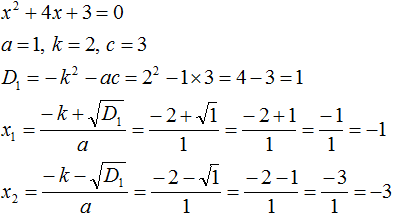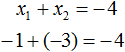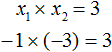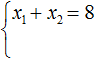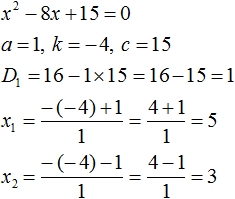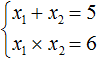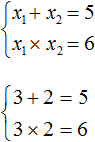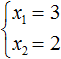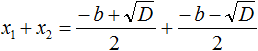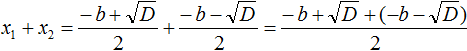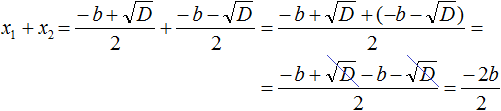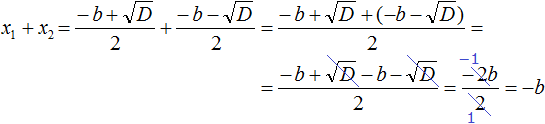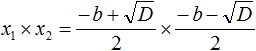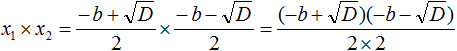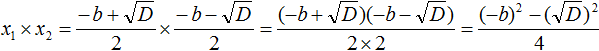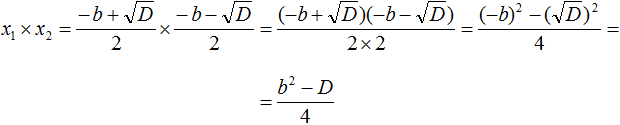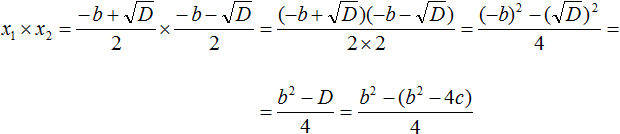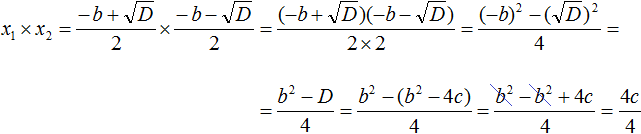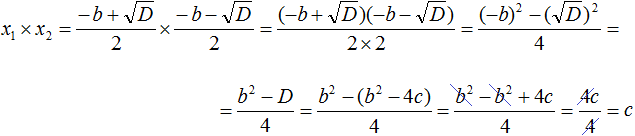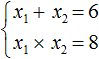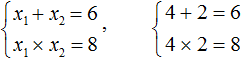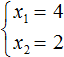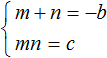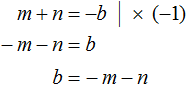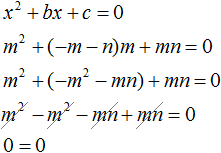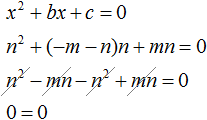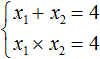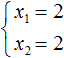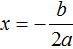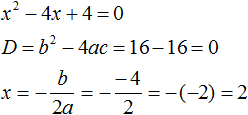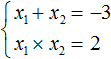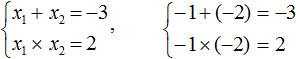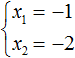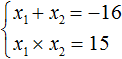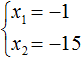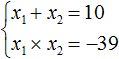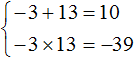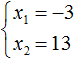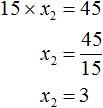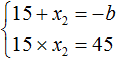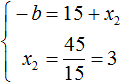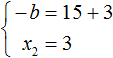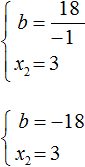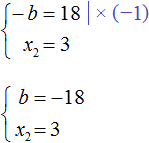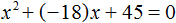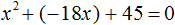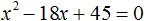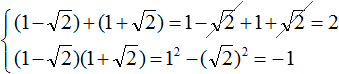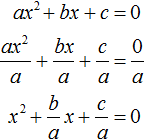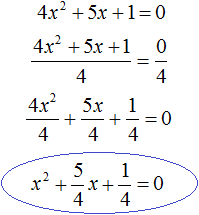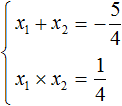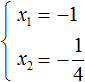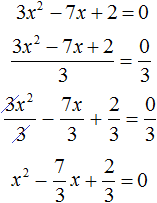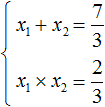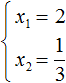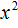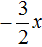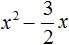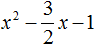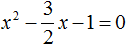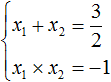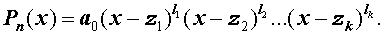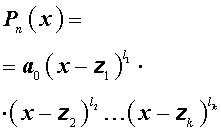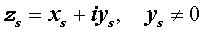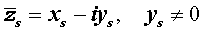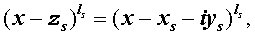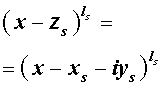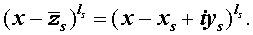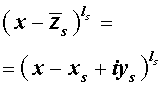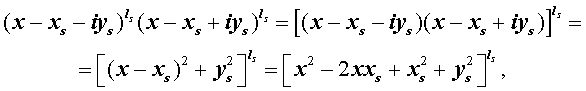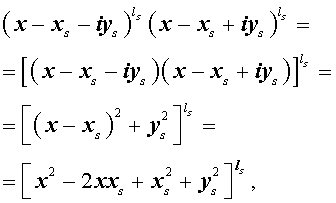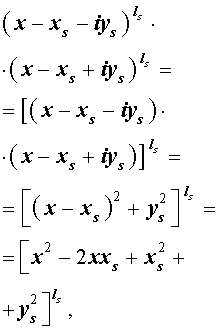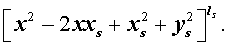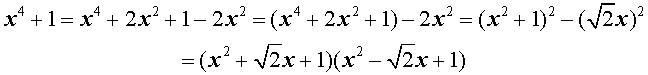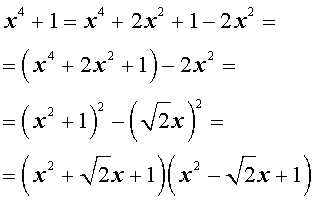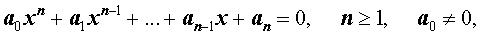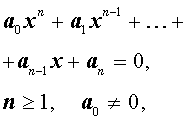- Что называют теоремой?
- Теорема Виета
- Доказательство теоремы Виета
- Теорема, обратная теореме Виета
- Примеры решения уравнений по теореме, обратной теореме Виета
- Когда квадратное уравнение неприведённое
- Разложение многочленов на множители. Формулы Виета
- Алгебраические уравнения
- Разложение многочленов на множители в комплексной области
- Разложение на множители многочленов с действительными коэффициентами
- Теорема (формулы) Виета
- Теорема Виета для уравнений третьей и четвертой степени
- Описание презентации по отдельным слайдам:
- Дистанционное обучение как современный формат преподавания
- Математика: теория и методика преподавания в образовательной организации
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Материал подходит для УМК
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- 💥 Видео
Видео:ТЕОРЕМА ВИЕТА ЗА 2 МИНУТЫСкачать

Что называют теоремой?
Если человек обнаружил в математике какую-нибудь закономерность, позволяющую быстро решить ту или иную задачу, то ему не следует говорить о том, что он сделал открытие. Потому что может случиться так, что эта закономерность работает только для определённых случаев, а для других не работает или вовсе решает задачу неправильно.
Чтобы поделиться своим открытием с другими людьми, найденную закономерность следует сформулировать в виде утверждения, а затем доказать это утверждение, приводя неоспоримые факты.
Сформулированное утверждение называют теоремой. А доказательство теоремы состоит из фактов, логических рассуждений и вычислений, которые не оспариваются.
Например, теоремой можно назвать следующее утверждение:
«Если числитель и знаменатель обыкновенной дроби умнóжить на какое-нибудь число, то значение данной дроби не измéнится».
А затем привести такое доказательство:
Пусть, имеется дробь 
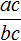

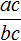
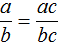
Для доказательства этого равенства воспользуемся основным свойством пропорции:
От перестановки мест сомножителей произведение не меняется. Поэтому в получившемся равенстве можно упорядочить правую часть по алфавиту:
Поскольку равенство 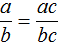

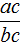
Видео:Теорема Виета для многочлена 3 порядка. 10 класс.Скачать

Теорема Виета
Французский математик Франсуа Виет выявил интересную взаимосвязь между коэффициентами приведённого квадратного уравнения и корнями этого же уравнения. Эта взаимосвязь представлена в виде теоремы и формулируется так:
Сумма корней приведённого квадратного уравнения x 2 + bx + c = 0 равна второму коэффициенту, взятому с противоположным знáком, а произведение корней равно свободному члену.
То есть, если имеется приведённое квадратное уравнение x 2 + bx + c = 0 , а его корнями являются числа x1 и x2 , то справедливы следующие два равенства:
Знак системы (фигурная скобка) говорит о том, что значения x1 и x2 удовлетворяют обоим равенствам.
Покажем теорему Виета на примере приведённого квадратного уравнения x 2 + 4x + 3 = 0 .
Мы пока не знаем какие корни имеет уравнение x 2 + 4x + 3 = 0 . Но по теореме Виета можно записать, что сумма этих корней равна второму коэффициенту 4 , взятому с противоположным знáком. Если коэффициент 4 взять с противоположным знáком, то получим −4 . Тогда:
А произведение корней по теореме Виета будет равно свободному члену. В уравнении x 2 + 4x + 3 = 0 свободным членом является 3 . Тогда:
Теперь проверим действительно ли сумма корней равна −4 , и равно ли произведение 3 . Для этого найдём корни уравнения x 2 + 4x + 3 = 0 . А для удобства воспользуемся формулами для чётного второго коэффициента:
Корнями уравнения являются числа −1 и −3 . По теореме Виета их сумма должна была равняться второму коэффициенту уравнения x 2 + 4x + 3 = 0 , взятому с противоположным знаком. Действительно, так оно и есть. Вторым коэффициентов в уравнении x 2 + 4x + 3 = 0 является 4 . Если взять его с противоположным знаком и приравнять сумму корней x1 + x2 к этому коэффициенту, то получается верное равенство:
А произведение корней −1 и −3 по теореме Виета должно было равняться свободному члену уравнения x 2 + 4x + 3 = 0 , то есть числу 3 . Видим, что это условие тоже выполняется:
Значит выражение 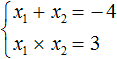
Рассмотрим квадратное уравнение x 2 − 8x + 15 = 0 . По теореме Виета сумма корней этого уравнения равна второму коэффициенту, взятому с противоположным знаком. Второй коэффициент равен −8 . Если взять его с противоположным знаком, то получим 8 . Тогда:
А произведение корней равно свободному члену. В уравнении x 2 − 8x + 15 = 0 свободным членом является 15 . Тогда:
Теперь проверим действительно ли сумма корней равна 8 , и равно ли произведение 15 . Для этого найдём корни данного уравнения. А для удобства воспользуемся формулами для чётного второго коэффициента. В этот раз пропустим нéкоторые подробные записи:
Видим, что корнями уравнения x 2 − 8x + 15 = 0 являются числа 5 и 3 . Их сумма равна 8 . То есть сумма корней равна второму коэффициенту уравнения x 2 − 8x + 15 = 0 , взятому с противоположным знаком.
А произведение чисел 5 и 3 равно 15 . То есть равно свободному члену уравнения x 2 − 8x + 15 = 0 .
Значит выражение 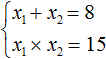
Замечание. Чтобы теорема Виета выполнялась, квадратное уравнение обязательно должно быть приведённым и иметь корни.
Например, рассмотрим квадратное уравнение x 2 − 2x + 4 = 0 . Напишем сумму и произведение корней этого уравнения:
Но уравнение x 2 − 2x + 4 = 0 не имеет корней, сумма которых равна 2, а произведение которых равно 4 . Убедиться в этом можно, вычислив дискриминант:
А значит записывать выражение 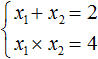
Теорема Виета полезна тем, что позволяет до начала решения узнать знаки корней уравнения.
Например, запишем для уравнения x 2 − 5x + 6 = 0 сумму и произведение его корней. Сумма корней равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:
Посмотрев на эти два равенства можно сразу понять, что оба корня должны быть положительными. Потому что произведение x1 × x2 = 6 будет выполняться только в двух случаях: если значения x1 и x2 положительны либо они оба отрицательны. Если эти значения будут отрицательными, то не будет выполняться равенство x1 + x2 = 5 , поскольку его правая часть равна положительному числу. А значения x1 и x2 должны удовлетворять как равенству x1 + x2 = 5 , так и равенству x1 × x2 = 6.
Ещё одна польза от теоремы Виета в том, что корни можно найти методом подбора. В данном примере корни должны быть такими, чтобы они удовлетворяли как равенству x1 + x2 = 5 так и равенству x1 × x2 = 6 . Очевидно, что таковыми являются корни 3 и 2
Доказательство теоремы Виета
Пусть дано приведённое квадратное уравнение x 2 + bx + c = 0 . Если его дискриминант больше нуля, то оно имеет два корня, сумма которых равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:
Вспомним формулы корней квадратного уравнения:
Найдём сумму корней x1 и x2 . Для этого подставим в выражение x1 + x2 вместо x1 и x2 соответствующие выражения из правой части формул корней квадратного уравнения. Не забываем, что в приведённом квадратном уравнении x 2 + bx + c = 0 старший коэффициент a равен единице. Тогда в процессе подстановки знаменатель станет равен просто 2
Запишем правую часть в виде дроби с одним знаменателем:
Раскроем скобки в числителе и приведём подобные члены:
Сократим дробь 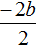
Теперь аналогично докажем, что произведение x1 × x2 равно свободному члену c .
Подставим вместо x1 и x2 соответствующие выражения из формул корней квадратного уравнения. Не забываем, что коэффициент a всё ещё равен единице:
Чтобы перемнóжить дроби, нужно перемнóжить их числители и знаменатели:
В числителе теперь содержится произведение суммы двух выражений и разности этих же выражений. Воспользуемся тождеством (a + b)(a − b) = a 2 − b 2 . Тогда в числителе полýчится 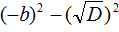
Теперь в числителе выражение (−b) 2 станет равно b 2 , а выражение 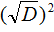
Но D равно b 2 − 4ac . Подстáвим это выражение вместо D , не забывая что a = 1 . То есть вместо b 2 − 4ac надо подставить b 2 − 4c
В получившемся выражении раскроем скобки в числителе и приведём подобные члены:
Сократим получившуюся дробь на 4
Таким образом, сумма корней приведённого квадратного уравнения x 2 + bx + c = 0 равна второму коэффициенту, взятому с противоположным знáком ( x1 + x2 = −b ), а произведение корней равно свободному члену ( x1 × x2 = c ). Теорема доказана.
Видео:Теорема Виета для уравнений высших степеней. Рациональные уравнения Часть 4 из 4Скачать

Теорема, обратная теореме Виета
Когда записана сумма и произведение корней приведённого квадратного уравнения, обычно начинается подбор подходящих корней к этому уравнению. В этот момент в работу включается так называемая теорема, обратная теореме Виета. Она формулируется так:
Если числа x1 и x2 таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знáком, а произведение чисел x1 и x2 равно свободному члену уравнения x 2 + bx + c = 0, то числа x1 и x2 являются корнями уравнения x 2 + bx + c = 0.
Обратные теоремы бывают поставлены так, что их утверждением является заключение первой теоремы.
Так, доказывая теорему Виета мы пришли к заключению, что сумма x1 и x2 равна −b , а произведение x1 и x2 равно c . В обратной же теореме это заключение служит утверждением.
Ранее мы решили уравнение x 2 − 5x + 6 = 0 и написали для него такую сумму и произведение корней:
А затем подобрали корни 3 и 2 . По сути мы применили теорему, обратную теореме Виета. Числа 3 и 2 таковы, что их сумма равна второму коэффициенту уравнения x 2 − 5x + 6 = 0 , взятому с противоположным знаком (числу 5 ), а произведение чисел 3 и 2 равно свободному члену (числу 6 ). Значит числа 3 и 2 являются корнями уравнения x 2 − 5x + 6 = 0 .
Пример 2. Решить квадратное уравнение x 2 − 6x + 8 = 0 по теореме, обратной теореме Виета.
В данном уравнении a = 1 . Значит квадратное уравнение является приведённым. Его можно решить по теореме, обратной теореме Виета.
Сначала запишем сумму и произведение корней уравнения. Сумма корней будет равна 6 , поскольку второй коэффициент исходного уравнения равен −6 . А произведение корней будет равно 8
Теперь имея эти два равенства можно подобрать подходящие корни. Они должны удовлетворять как равенству x1 + x2 = 6 , так и равенству x1 × x2 = 8
Подбор корней удобнее выполнять с помощью их произведения. Используя равенство x1 × x2 = 8 нужно найти такие x1 и x2 , произведение которых равно 8.
Число 8 можно получить если перемножить числа 4 и 2 либо 1 и 8.
4 × 2 = 8
1 × 8 = 8
Но значения x1 и x2 надо подбирать так, чтобы они удовлетворяли не только равенству x1 × x2 = 8 , но и равенству x1 + x2 = 6 .
Сразу делаем вывод, что значения 1 и 8 не годятся, поскольку они хоть и удовлетворяют равенству x1 × x2 = 8 , но не удовлетворяют равенству x1 + x2 = 6 .
Зато значения 4 и 2 подходят как равенству x1 × x2 = 8 , так и равенству x1 + x2 = 6 , поскольку эти значения удовлетворяют обоим равенствам:
Значит корнями уравнения x 2 − 6x + 8 = 0 являются числа 4 и 2 .
Обратная теорема, как и любая теорема нуждается в доказательстве. Докажем теорему, обратную теореме Виета. Для удобства корни x1 и x2 обозначим как m и n . Тогда утверждение теоремы, обратной теореме Виета примет следующий вид:
Если числа m и n таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знáком, а произведение чисел m и n равно свободному члену уравнения x 2 + bx + c = 0, то числа m и n являются корнями уравнения x 2 + bx + c = 0
Для начала запишем, что сумма m и n равна −b , а произведение mn равно c
Чтобы доказать, что числа m и n являются корнями уравнения x 2 + bx + c = 0 , нужно поочередно подстáвить буквы m и n в это уравнение вместо x , затем выполнить возможные тождественные преобразования. Если в результате преобразований левая часть станет равна нулю, то это будет означать, что числа m и n являются корнями уравнения x 2 + bx + c = 0 .
Помимо букв m и n нам нужно знать чему равен параметр b . Выразим его из равенства m + n = −b . Легче всего это сделать, умножив обе части этого равенства на −1
Теперь всё готово для подстановок. Подстáвим m в уравнение x 2 + bx + c = 0 вместо x , а выражение −m − n подставим вместо b
Видим, что при x = m получается верное равенство. Значит число m является корнем уравнения x 2 + bx + c = 0 .
Аналогично докажем, что число n является корнем уравнения x 2 + bx + c = 0 . Подставим вместо x букву n , а вместо c подставим mn , поскольку c = mn .
Видим, что при x = n тоже получается верное равенство. Значит число n является корнем уравнения.
Следовательно, числа m и n являются корнями уравнения x 2 + bx + c = 0 .
Видео:Теорема Виета. 8 класс.Скачать

Примеры решения уравнений по теореме, обратной теореме Виета
Пример 1. Решить квадратное уравнение x 2 − 4x + 4 = 0 по теореме, обратной теореме Виета.
Запишем сумму корней x1 и x2 и приравняем её к второму коэффициенту, взятому с противоположным знаком. Также запишем произведение корней x1 и x2 и приравняем его к свободному члену :
В данном примере очевидно, что корнями являются числа 2 и 2 . Потому что их сумма равна 4 и произведение равно 4
Значение x1 совпадает с x2 . Это тот случай, когда квадратное уравнение имеет только один корень. Если мы попробуем решить данное уравнение с помощью формул корней квадратного уравнения, то обнаружим что дискриминант равен нулю, и корень вычисляется по формуле
Данный пример показывает, что теорема обратная теореме Виета, работает и для уравнений, имеющих только один корень. Признаком того, что квадратное уравнение имеет только один корень является то, что значения x1 и x2 совпадают.
Пример 2. Решить уравнение x 2 + 3x + 2 = 0 по теореме, обратной теореме Виета.
Запишем сумму и произведение корней данного уравнения:
Теперь подберём значения x1 и x2 . Здесь начинается самое интересное. Произведение корней равно 2 . Число 2 можно получить перемножив 1 и 2 . Но сумма корней x1 + x2 равна отрицательному числу −3 . Значит значения 1 и 2 не подходят.
Сумма бывает отрицательной если оба слагаемых отрицательны либо отрицательным является одно слагаемое, модуль которого больше.
Если подберём корни с разными знаками, то не будет выполняться равенство x1 × x2 = 2 .
Если подберем положительные корни, то будет выполняться равенство x1 × x2 = 2 , но не будет выполняться равенство x1 + x2 = −3 .
Очевидно, что корнями являются два отрицательных числа. Произведение отрицательных чисел есть положительное число. А сумма отрицательных чисел есть отрицательное число.
Тогда равенствам будут удовлетворять числа −1 и −2 .
Итак, корнями являются числа −1 и −2
Пример 3. Решить уравнение x 2 + 16x + 15 = 0 по теореме, обратной теореме Виета.
Запишем сумму и произведение корней данного уравнения:
Как и в прошлом примере сумма корней равна отрицательному числу, а произведение корней — положительному числу.
Произведение бывает положительным если оба сомножителя положительны либо оба сомножителя отрицательны. Первый вариант отпадает сразу, поскольку сумма корней равна отрицательному числу. Тогда получается, что оба корня будут отрицательными. Попробуем подобрать их.
Число 15 можно получить, если перемножить числа −1 и −15 или (−3) и (−5) . В данном случае подходит первый вариант, поскольку сумма чисел −1 и −15 равна −16 , а их произведение равно 15 . Значит корнями уравнения x 2 + 16x + 15 = 0 являются числа −1 и −15
Пример 4. Решить уравнение x 2 − 10x − 39 = 0 по теореме, обратной теореме Виета.
Запишем сумму и произведение корней данного уравнения:
Произведение корней равно отрицательному числу. Значит один из корней является отрицательным. Число −39 можно получить если перемножить числа −3 и 13 либо −13 и 3 . Из этих комбинаций больше годится комбинация −3 и 13 , поскольку при перемножении этих чисел получается −39 , а при сложении 10
Значит корнями уравнения x 2 − 10x − 39 = 0 являются числа −3 и 13
Пример 5. Первый корень уравнения x 2 + bx + 45 = 0 равен 15 . Найти второй корень этого уравнения, а также значение коэффициента b .
По теореме Виета произведение корней приведённого квадратного уравнения равно свободному члену. В данном случае это произведение равно 45
При этом один из корней уже известен — это корень 15 .
Тогда второй корень будет равен 3 , потому что число 45 получается, если 15 умножить на 3
Этот второй корень также можно было бы получить, выразив из равенства 15 × x2 = 45 переменную x2
Теперь определим значение коэффициента b . Для этого напишем сумму корней уравнения:
По теореме Виета сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком. Если сумма корней равна 18, а 18 это положительное число, то в самóм уравнении этот коэффициент будет отрицательным:
Обычно решение к такой задаче записывают так. Сначала записывают основную теорему Виета в виде суммы и произведения корней:
Затем в это выражение подставляют имеющиеся известные значения. В нашем случае известно, что первый корень равен 15 , а свободный член уравнения x 2 + bx + 45 = 0 равен 45
Из этой системы следует найти x2 и b . Выразим эти параметры:
Из этой системы мы видим, что x2 равно 3. Подставим его в первое равенство:
Теперь из первого равенства мы видим, что −b равно 18
Но нас интересует b , а не −b . Следует помнить, что −b это −1b . Чтобы найти b нужно 18 разделить на −1 . Тогда b станет равно −18
Этот же результат можно получить если в выражении 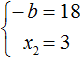
Теперь возвращаемся к исходному уравнению x 2 + bx + 45 = 0 и подставляем найденное значение b
Выполним умножение −18 на x . Получим −18x
Пример 6. Используя теорему Виета, написать приведённое квадратное уравнение, корнями которых являются числа 2 и 8 .
В этом задании корни уже известны. То есть x1 = 2 , x2 = 8 . По ним надо составить квадратное уравнение вида x 2 + bx + c = 0 .
Запишем сумму и произведение корней:
По теореме Виета сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком. Если сумма корней 2 и 8 равна 10 , то в самóм уравнении число 10 должно быть с противоположным знаком. Значит b = −10 .
Произведение корней по теореме Виета равно свободному члену. У нас это произведение равно 16 .
Значит b = −10 , c = 16 . Отсюда:
Пример 7. Используя теорему Виета, написать приведённое квадратное уравнение, корнями которых являются числа 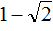
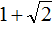
Запишем сумму и произведение корней:
Сумма корней равна 2. Тогда в уравнении второй коэффициент будет равен −2. А произведение корней равно −1. Значит свободный член будет равен −1. Тогда:
Видео:КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать

Когда квадратное уравнение неприведённое
Теорема Виета выполняется только тогда, когда квадратное уравнение является приведённым.
Если квадратное уравнение не является приведённым, но всё равно возникла необходимость применить теорему Виета, то обе части неприведённого квадратного уравнения следует разделить на коэффициент, который располагается перед x 2 .
Если к примеру в квадратном уравнении a x 2 + bx + c = 0 коэффициент a не равен единице, то данное уравнение является неприведённым. Чтобы сделать его приведённым, надо разделить обе его части на коэффициент, который располагается перед x 2 , то есть на a
Получилось уравнение 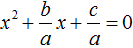


Например, решим квадратное уравнение 4x 2 + 5x + 1 = 0 . Это уравнение не является приведённым. Приведённым оно станет, если разделить обе его части на коэффициент, который располагается перед x 2 , то есть на 4
Получили приведённое квадратное уравнение. В нём второй коэффициент равен 

Отсюда методом подбора находим корни −1 и
Возможно этот метод вы редко будете использовать при решении квадратных уравнений. Но знать о нём не помешает.
Пример 2. Решить квадратное уравнение 3x 2 − 7x + 2 = 0
Данное уравнение не является приведённым, а значит его пока нельзя решить по теореме, обратной теореме Виета.
Сделаем данное уравнение приведенным. Разделим обе части на коэффициент, который располагается перед x 2
Получили уравнение 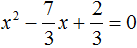
Отсюда методом подбора находим корни 2 и
Пример 3. Решить квадратное уравнение 2x 2 − 3x − 2 = 0
Это неприведённое квадратное уравнение. Чтобы сделать его приведённым, нужно разделить обе его части на 2 . Сделать это можно в уме. Если 2x 2 разделить на 2 , то полýчится x 2
Далее если −3x разделить на 2 , то полýчится 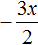
Далее если −2 разделить на 2 , то полýчится −1
Прирáвниваем получившееся выражение к нулю:
Теперь применяем теорему Виета. Сумма корней будет равна второму коэффициенту, взятому с противоположным знáком, а произведение корней свободному члену:
Отсюда методом подбора находим корни 2 и
Видео:Уравнение четвертой степениСкачать

Разложение многочленов на множители. Формулы Виета
 Алгебраические уравнения Алгебраические уравнения |
 Основная теорема алгебры. Разложение многочленов на линейные множители в комплексной области Основная теорема алгебры. Разложение многочленов на линейные множители в комплексной области |
 Разложение на множители многочленов с действительными коэффициентами Разложение на множители многочленов с действительными коэффициентами |
 Теорема (формулы) Виета Теорема (формулы) Виета |
Видео:ТЕОРЕМА ВИЕТА // Как решать Квадратные Уравнения по АЛГЕБРЕ 8 классСкачать

Алгебраические уравнения
Пусть n – произвольное натуральное число. Рассмотрим многочлен n – ой степени от переменной x
| Pn (x) = = a0 x n + a1 x n –1 + + … + an –1 x + an , | (1) |
| a0 , a1 , … , an –1 , an | (2) |
Заметим, что в этом случае коэффициент a0 отличен от нуля, и введем следующее определение.
Определение 1 . Алгебраическим уравнением степени n с неизвестным x называют уравнение вида
| Pn (x) = 0 . | (3) |
Определение 2 . Корнем уравнения (3) называют вещественное или комплексное число α , для которого
Определение 3 . Число α называют корнем кратности k уравнения (3), если справедливо равенство
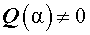
Видео:Теорема Виета, формула D/4 и другие хитростиСкачать

Разложение многочленов на множители в комплексной области
Основная теорема алгебры (теорема Гаусса) утверждает, что любое алгебраическое уравнение вида (3) имеет n корней, при условии, что каждый корень считается столько раз, какова его кратность.
– полный набор корней уравнения (3), а
– их кратности, то, во-первых,
а, во-вторых, справедливо равенство
Замечание . Линейными множителями называют многочлены первой степени
входящие в формулу (4), а саму формулу (4) называют формулой разложения многочленов на линейные множители в комплексной области .
Видео:#131 Урок 56. Теорема Виета. Нахождение значения выражения при помощи теоремы Виета. Алгебра 8 классСкачать

Разложение на множители многочленов с действительными коэффициентами
Рассмотрим теперь многочлены степени 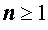
Тогда справедливо следующее
Утверждение . Если комплексное число
является корнем кратности ls многочлена с вещественными коэффициентами, то и комплексно сопряженное число
является корнем этого многочлена, причем тоже кратности ls .
Из утверждения вытекает, что в разложение (4) степень каждого бинома, содержащая комплексный корень zs и имеющая вид
входит в паре со степенью бинома, содержащей комплексно сопряженный корень 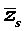
то произведение каждой пары биномов (5) и (6), входящей в формулу (4), даёт степень квадратного трехчлена с вещественными коэффициентами:
Следствие . Каждый многочлен ненулевой степени, коэффициенты которого являются вещественными числами, разлагается на множители, являющиеся многочленами с вещественными коэффициентами первой или второй степени.
Пример . Разложить на множители многочлен четвертой степени
Видео:Как решать уравнения 4 степени Решите уравнение четвертой степени Разложить на множители Безу столбиСкачать

Теорема (формулы) Виета
Снова рассмотрим уравнение n – ой степени от переменной x
и, немного изменив предыдущие обозначения, предположим, что
| z1 , z2 , … , zn –1 , zn | (8) |
— его корни, причем в записи (8) каждый корень взят столько раз, какова его кратность.
Тогда из формулы (4) вытекают следующие равенства, которые называют формулами Виета для уравнения n – ой степени :
Видео:Теорема Виета за 4 минуты с примерами. Как решать квадратные уравнения быстрее учителя.Скачать

Теорема Виета для уравнений третьей и четвертой степени
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Теорема Виета для уравнений третьей и четвертой степени Презентация по теме
Цель Научиться решать уравнения третьей и четвертой степени, используя формулы Виета.
Задачи Знакомство с научным вкладом Франсуа Виета. Вспомнить формулы Виета для приведенного квадратного уравнения. Ознакомиться с формулой для решения приведенного кубического уравнения. Ознакомиться с формулой для решения приведенного уравнения четвертой степени.
Франсуа Виет Франсуа Виет(1540—1603) — французский математик. В 1591 году ввёл буквенные обозначения не только для неизвестных величин, но и для коэффициентов уравнений; благодаря этому стало впервые возможным выражение свойств уравнений и их корней общими формулами. Ему принадлежит установление единообразного приёма решения уравнений 2-й, 3-й и 4-й степеней. В тригонометрии Франсуа Виет дал полное решение задачи об определении всех элементов плоского или сферического треугольника по трём данным.
Приведенное квадратное уравнение
Приведенное кубическое уравнение Если x1, x2, x3 – корни кубического уравнения x3 + bx2 + cx + d = 0, то
Если x1, x2, x3, x4 – корни уравнения четвертой степени x4 + bx3 + cx2 + dx + e = 0, то Приведенное уравнение четвертой степени
Вывод В данной работе мы достигли поставленных целей: я узнала о научной деятельности Ф. Виета, его вкладе в математику, ознакомилась с формулами для решения приведенных уравнений третьей и четвертой степени, мы закрепили новые знания, с помощью решения задач. Но при этом нужно отметить, что данный метод не всегда эффективен, т.к. с его помощью в некоторых ситуациях подобрать корни сложно или почти невозможно. Например: 1) x3 + 13×2 + 27x + 1 = 0 x1 = — 10,417 x2 = — 0,038 x3 = — 2,545
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 949 человек из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 681 человек из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 314 человек из 70 регионов
Ищем педагогов в команду «Инфоурок»
Видео:Теорема БезуСкачать

Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 566 551 материал в базе
Материал подходит для УМК
«Алгебра», Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др.
§ 29. Приведённое квадратное уравнение. Теорема Виета
Другие материалы
- 16.05.2019
- 438
- 0
- 16.05.2019
- 1465
- 1
- 13.05.2019
- 6618
- 142
- 13.05.2019
- 2101
- 38
- 12.05.2019
- 557
- 39
- 10.05.2019
- 1869
- 103
- 10.05.2019
- 2636
- 50
- 30.04.2019
- 376
- 1
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 20.05.2019 3484
- PPTX 1.6 мбайт
- 82 скачивания
- Оцените материал:
Настоящий материал опубликован пользователем Семикова Наталия Геннадиевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 5 лет и 4 месяца
- Подписчики: 0
- Всего просмотров: 9346
- Всего материалов: 8
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Как решать уравнения четвёртой степени. Формула Феррари | #БотайСоМной #026 | Борис ТрушинСкачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Онлайн-конференция о создании школьных служб примирения
Время чтения: 3 минуты
В Воронеже продлили удаленное обучение для учеников 5-11-х классов
Время чтения: 1 минута
Рособрнадзор не планирует переносить досрочный период ЕГЭ
Время чтения: 0 минут
У 76% российских учителей оклад ниже МРОТ
Время чтения: 2 минуты
ЕГЭ в 2022 году будут сдавать почти 737 тыс. человек
Время чтения: 2 минуты
Количество бюджетных мест в вузах по IT-программам вырастет до 160 тыс.
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
💥 Видео
5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Теорема Виета. Алгебра, 8 классСкачать

Математика | Кубические уравнения по методу СталлонеСкачать

Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Обратная теорема Виета - ЛЕГКО!Скачать

Теорема ВиетаСкачать

✓ Как решать кубические уравнения. Формула Кардано | Ботай со мной #025 | Борис ТрушинСкачать