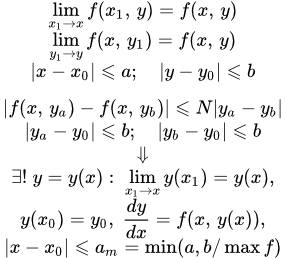Теорема существования и единственности дифференциальных уравнений пикара

Видео:Асташова И. В. - Дифференциальные уравнения I - Теорема существования и единственности Пикара - 1Скачать

Теорема Коши существования и единственности решения дифференциального уравнения первого порядка

Впервые существование решения дифференциального уравнения было доказано Коши. Приводимое ниже доказательство основано на методе последовательных приближений, который принадлежит Пикару. Этот метод имеет самостоятельное значение, поскольку позволяет получить приближенное решение дифференциального уравнения.

Видео:Асташова И. В. - Дифференциальные уравнения I - Теорема существования и единственности Пикара - 2Скачать

Формулировка теоремы

Пусть дано дифференциальное уравнение первого порядка:
(1)
с начальным условием
(1.1) .
Пусть – непрерывная функция двух переменных в замкнутой области :

и, следовательно, ограничена некоторым положительным значением :
(2) .
И пусть функция удовлетворяет условию Липшица:
(3) ,
.
Тогда существует единственное решение уравнения (1):
,
удовлетворяющее начальному условию , определенное и непрерывное для значений в интервале:
,
где есть наименьшее из двух чисел и .

Условие Липшица

Рассмотрим условие Липшица. Оно имеет вид:
(3) ,
где – положительное число;
, и – любые значения из области :
, , .

Смысл условия Липшица легко понять, если записать его в виде:
(3.1) .
При некотором фиксированном значении переменной , функция является функцией от переменной : . Пусть мы имеем график этой функции. Возьмем две точки, принадлежащие , на этом графике и проведем через них прямую. Тогда угол между прямой и осью ограничен некоторым значением , которое меньше . При таком ограничении график не имеет вертикальных касательных и скачков. А в тех точках, где существует частная производная , она ограничена:
.

Если в области функция имеет непрерывную частную производную , то в этой области выполняется условие Липшица (3).
Для доказательства заметим, что поскольку частная производная непрерывна в замкнутой области, то она ограничена:
.
По теореме Лагранжа о конечных приращениях, имеем:
,
где частные производные вычисляются в некоторой точке , в которой переменная принадлежат интервалу между и :
.
Тогда:
.

Видео:Линейная алгебра. Алексей Савватеев и Александр Тонис. Лекция 13.4. Существов. и единств. решения ДУСкачать

Доказательство существования решения

Приведем исходное уравнение (1) с начальным условием (1.1) к интегральному уравнению. Левая и правая части (1) являются функциями от . Заменим на :
.
Интегрируем это уравнение по от до :
;
Подставим начальное условие . В результате получим интегральное уравнение:
(4) .

Покажем, что интегральное уравнение (4) эквивалентно дифференциальному уравнению (1) с начальным условием (1.1). Для этого нужно показать, что из (1) и (1.1) следует (4) и из (4) следует (1) и (1.1). То, что из (1) и (1.1) следует (4) мы уже показали. Осталось показать, что из (4) следует (1) и (1.1). Для этого подставим в (4) . Получим начальное условие (1.1). Продифференцировав обе части уравнения (4) по , получаем уравнение (1).

Далее мы пытаемся найти решение уравнения (4) с помощью последовательных приближений. Для этого определяем ряд функций от переменной по формулам:
(5.1) ;
(5.2) ;
(5.3) ;
.
(5.n) .
Мы предполагаем, что при , стремится к решению уравнения (4):
(6) ,
где – решение уравнения (4). Если мы докажем это, то мы докажем существование решения.

Доказательство существования решения будем проводить в два этапа:
1> вначале докажем, что предел (6) существует;
2) затем докажем, что удовлетворяет уравнению (4):
.

1) Доказательство существования предела y_n при n стремящемся к бесконечности

Сведем последовательные приближения (5.1) – (5.n) к сумме ряда. Для этого пишем:

.
Таким образом нам нужно доказать, что ряд
(7)
сходится при .

Сначала покажем, что при , последовательные приближения принадлежат интервалу .
Действительно, при имеем:
.
Поскольку есть наименьшее из двух чисел и , то и
.

Далее, поскольку принадлежит интервалу , то . Тогда, аналогично предыдущему,
.
Отсюда
.

Далее, по индукции, поскольку принадлежат интервалу , то и
.
Отсюда
.

Итак, мы доказали, что последовательные приближения принадлежат интервалу
.
Теперь мы можем оценить члены ряда (7), применяя условие Липшица.

Для первого члена имеем:
;
(8.1) .
Для второго члена применяем условие Липшица и оценку (8.1):

;
(8.2) .
Для третьего члена применяем, аналогично, условие Липшица и оценку (8.2):

;
(8.3) .

Далее применим метод индукции. Пусть
(8.n) .
Тогда

;
(8.n+1) .
Итак, поскольку (8.n) справедливо для и из (8.n) следует (8.n+1), то (8.n) выполняется для любых .

Запишем ряд (7) в виде:
(7.1) ,
где .
Применим (8.n) и заменим наибольшим допустимым значением :
.
Тогда каждый член ряда (7.1) ограничен по модулю членом ряда
(9) .
Исследуем ряд (9) на сходимость. Применим признак Даламбера:
.
Итак, ряд (9) сходится. Поскольку все члены ряда (7.1), начиная со второго, по абсолютной величине меньше членов сходящегося ряда (9), то, в силу критерия Вейерштрасса, ряд (7.1) сходится равномерно для всех , удовлетворяющих условию . Поскольку интеграл есть непрерывная функция от верхнего предела, то каждый член ряда (7.1) есть непрерывная функция от . Поэтому предел
(10)
существует и является непрерывной функцией от .

2) Доказательство того, что Y является решением (4)

Рассмотрим уравнение (5.n):
(5.n) .
Докажем, что при , это уравнение стремится к уравнению
(11) .

В силу (10) левая часть уравнения (5.n) стремится к .

Теперь покажем, что
.

Перепишем правую часть (5.n):
.
Далее заметим, что поскольку все принадлежат закрытому интервалу , то и принадлежит этому интервалу, . Поэтому мы можем применить условие Липшица.

Оценим абсолютную величину последнего члена:

.
Поскольку, при , стремится к равномерно, то для любого положительного числа можно указать такое натуральное число , что для всех ,
.
Тогда
.
Поскольку произвольно, то

Поэтому
.
То есть при уравнение
(5.n)
принимает вид
(11) .

Видео:Лукьяненко Д. В. - Дифференциальные уравнения - Лекция 2Скачать

Доказательство единственности решения

Предположим, что уравнение
(4)
имеет два решения и , различающиеся в некоторой точке , принадлежащей интервалу .
Рассмотрим функцию
.
Будем считать, что . В противном случае поменяем местами и .
Поскольку и непрерывны, то и непрерывная функция. Поэтому она отлична от нуля в некотором интервале, содержащем точку :
при .
Поскольку , то . То есть точка не принадлежит этому интервалу.

Если , то преобразуем (4) следующим образом:
,
где
.
Если переобозначить постоянные
,
то получим задачу (4), для которой
;
при ,
где – некоторое число, не превосходящее .

Если , то поступаем аналогично:
,
Переобозначим постоянные:
.
Получаем задачу (4), для которой
;
при ,
где – некоторое число, не меньшее .

Итак, мы имеем:
;
при ( или при ).
Далее возьмем произвольное положительное число ( или ) и рассмотрим закрытый интервал ( или ). Поскольку функция непрерывна, то она достигает наибольшего значения в одной из точек этого интервала:
( или ).

Сделаем оценку, применяя уравнение (4) и условие Липшица:

;
.
Поскольку , то разделим на :
.
Возникает противоречие, поскольку при это неравенство не выполняется.

Следовательно, не может иметь отличных от нуля значений. Поэтому . Что и требовалось доказать.

Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.

Автор: Олег Одинцов . Опубликовано: 04-06-2016 Изменено: 20-06-2016

Видео:Теорема Пикара для задачи КошиСкачать

Теорема существования и единственности: доказательство, примеры и упражнения

Теорема существования и единственности: доказательство, примеры и упражнения — Наука

Видео:Практика 9 Теорема ПикараСкачать

Содержание:

В Теорема существования и единственности устанавливает необходимые и достаточные условия для того, чтобы дифференциальное уравнение первого порядка с заданным начальным условием имело решение, и это решение было единственным.

Однако теорема не дает никаких методов или указаний, как найти такое решение. Теорема существования и единственности также распространяется на дифференциальные уравнения высшего порядка с начальными условиями, известную как задача Коши.

Формальная формулировка теоремы существования и единственности следующая:

«Для дифференциального уравнения у ‘(х) = е (х, у) с начальным условием у (а) = б, существует хотя бы одно решение в прямоугольной области плоскости XY содержащий в точку (а, б)да уж f (x, y) это непрерывно в этом регионе. И если частная производная от F в отношении Y: g = ∂f / ∂инепрерывно в той же прямоугольной области, то решение единственно в окрестности точки (а, б) содержание в области непрерывности F Y грамм.”

Полезность этой теоремы заключается, во-первых, в знании того, в каких областях плоскости XY может существовать решение, а также в знании, является ли найденное решение единственно возможным или существуют другие.

Обратите внимание, что если условие единственности не выполняется, теорема не может предсказать, сколько всего решений имеет задача Коши: возможно, это одно, два или более.

Видео:3. Условия существования и единственности решения задачи КошиСкачать

Доказательство теоремы существования и единственности.

Известны два возможных доказательства этой теоремы: одно из них — доказательство Шарля Эмиля Пикара (1856-1941), а другое — Джузеппе Пеано (1858-1932), основанное на работах Огюстена Луи Коши (1789-1857). .

Примечательно, что в доказательстве этой теоремы принимали участие самые блестящие математические умы девятнадцатого века, так что интуитивно понятно, что ни одно из них не является простым.

Чтобы формально доказать теорему, необходимо сначала установить ряд более сложных математических понятий, таких как функции липшицевого типа, банаховы пространства, теорема существования Каратеодори и некоторые другие, которые выходят за рамки статьи.

Большая часть дифференциальных уравнений, которые используются в физике, имеют дело с непрерывными функциями в интересующих нас областях, поэтому мы ограничимся демонстрацией того, как теорема применяется к простым уравнениям.

Видео:Существование и единственность Теорема и задачи ДзСкачать

Примеры

Видео:Теорема Пикара. Часть 1.Скачать

— Пример 1

Рассмотрим следующее дифференциальное уравнение с начальным условием:

у ‘(х) = — у; с участиему (1) = 3

Есть ли решение этой проблемы? Это единственно возможное решение?

Видео:Теорема Пикара. Часть 3. Единственность и пример.Скачать

Ответы

Во-первых, оценивается существование решения дифференциального уравнения и то, что оно также удовлетворяет начальному условию.

В этом примереf (x, y) = — y условие существования требует знания того,f (x, y) непрерывна в области плоскости XY содержащий точку с координатами x = 1, y = 3.

Но f (x, y) = — y это аффинная функция, который является непрерывным в области действительных чисел и существует во всем диапазоне действительных чисел.

Отсюда заключаем, что f (x, y) непрерывна в R 2 , поэтому теорема гарантирует существование хотя бы одного решения.

Зная это, необходимо оценить, уникально ли решение или, наоборот, их больше одного. Для этого необходимо вычислить частную производную от F по переменной Y:

Такг (х, у) = -1 которая является постоянной функцией, которая также определена для всех R 2 и там он тоже непрерывен. Отсюда следует, что теорема существования и единственности гарантирует, что эта задача с начальным значением действительно имеет единственное решение, хотя и не сообщает нам, что это такое.

Видео:05.09.2022 Теоремы существования и единственности. Приближение Пикара.Скачать

— Пример 2

Рассмотрим следующее обыкновенное дифференциальное уравнение первого порядка с начальным условием:

Есть ли решение у (х) для этой проблемы? Если да, то определите, один или несколько.

Видео:Лекция 1.7 Теорема Пикара существования и единственности 1. Диффуры – И.В. АсташоваСкачать

Ответить

Рассмотрим функцию f (x, y) = 2√y. Функция F определяется только дляy≥0, поскольку мы знаем, что отрицательное число не имеет действительного корня. В дальнейшемf (x, y) непрерывна в верхней полуплоскости R 2 включая ось X, поэтому теорема существования и единственности гарантирует хотя бы одно решение в этом регионе.

Теперь начальное условие x = 0, y = 0 находится на краю области решения. Затем берем частную производную f (x, y) по y:

В этом случае функция не определена для y = 0, где именно находится начальное условие.

Что говорит нам теорема? Это говорит нам, что, хотя мы знаем, что есть по крайней мере одно решение в верхней полуплоскости оси X, включая ось X, поскольку условие уникальности не выполняется, нет гарантии, что будет уникальное решение.

Это означает, что может быть одно или несколько решений в области непрерывности f (x, y). И, как всегда, теорема не говорит нам, какими они могли быть.

Видео:Лекция 4. Теоремы существования и единственности.Скачать

Решенные упражнения

Видео:3 Теорема существования и единственности решения задачи Коши неоднородного линейного ОДУ первого поСкачать

— Упражнение 1

Решите задачу Коши из примера 1:

у ‘(х) = — у; с участиему (1) = 3.

Найдите функцию y (x), которая удовлетворяет дифференциальному уравнению и начальному условию.

Видео:Дифференциальные уравнения. Теоретический билет 3/6. Теорема ПикараСкачать

Решение

В Примере 1 было определено, что эта проблема имеет решение и к тому же уникальна. Чтобы найти решение, первое, что нужно отметить, это то, что это дифференциальное уравнение первой степени разделимых переменных, которое записывается следующим образом:

dy / dx = — y → dy = -y dx

Разделение между и в обоих членах для разделения имеющихся переменных:

Неопределенный интеграл применяется к обоим членам:

Решая неопределенные интегралы, мы имеем:

где C — постоянная интегрирования, которая определяется начальным условием:

ln (3) = -1 + C, то есть C = 1 + ln (3)

Подставив значение C и переставив его, остается:

ln (y) — ln (3) = -x + 1

Применяя следующее свойство логарифмов:

Разница логарифмов — это логарифм частного

Вышеупомянутое выражение можно переписать так:

Экспоненциальная функция с основанием e в обоих членах применяется для получения:

Это единственное решение уравнения y ’= -y с y (1) = 3. График этого решения показан на рисунке 1.

Видео:Волков В. Т. - Дифференциальные уравнения - Теорема о существовании и единственности решенияСкачать

— Упражнение 2.

Найдите два решения проблемы, поставленной в примере 2:

Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Решение

Это также уравнение разделимых переменных, которое в дифференциальной форме выглядит так:

Остается принять неопределенный интеграл в обоих членах:

Откуда ты это знаешь y≥0 в области решения имеем:

Но так как начальное условие x = 0, y = 0 должно выполняться, то константа C равна нулю и остается следующее решение:

Но это решение не единственное, функция y (x) = 0 также является решением поставленной задачи. Теорема существования и единственности, примененная к этой проблеме в примере 2, уже предсказывала, что может быть более одного решения.

Видео:Лекция 1.8 Теорема Пикара существования и единственности 2. Диффуры – И.В. АсташоваСкачать

Ссылки

1. Коддингтон, граф А.; Левинсон, Норман (1955), Теория обыкновенных дифференциальных уравнений, Нью-Йорк: McGraw-Hill.
2. Энциклопедия математики. Теорема Коши-Липшица. Получено с: encyclopediaofmath.org
3. Lindelöf, Sur l’application de la méthode des Approvalations Aux équations différentielles ordinaires du premier ordre; Comptes rendus hebdomadaires des séances de l’Académie des Sciences. Т. 116, 1894 г., стр. 454–457. Получено с: gallica.bnf.fr.
4. Википедия. Метод последовательного приближения Пикара. Получено с: es.wikipedia.com
5. Википедия. Теорема Пикара-Линделёфа. Получено с: es.wikipedia.com.
6. Зилл, Д. 1986. Элементарные дифференциальные уравнения с приложениями, Прентис Холл.

Патологическое пристрастие к азартным играм: симптомы, причины, последствия и лечение

Теорема Пикара (дифференциальные уравнения)

Связанные понятия

Параболические уравнения — класс дифференциальных уравнений в частных производных. Один из видов уравнений, описывающих нестационарные процессы.

В настоящее время отсутствует единое определение точно решаемой задачи для всех разделов математики. Это обусловлено особенностями самих задач и методов поиска их решения. Вместе с тем базовые теоремы, определяющие наличие и единственность решений, строятся на общих принципах, что будет показано ниже.

Эллиптические уравнения — класс дифференциальных уравнений в частных производных, описывающих стационарные процессы.

Точное нахождение первообразной (или интеграла) произвольных функций — процедура более сложная, чем «дифференцирование», то есть нахождение производной. Зачастую, выразить интеграл в элементарных функциях невозможно.

Важнейшими с точки зрения приложений характеристических функций к выводу асимптотических формул теории вероятностей являются две предельные теоремы — прямая и обратная. Эти теоремы устанавливают, что соответствие, существующее между функциями распределения и характеристическими функциями, не только взаимно однозначно, но и непрерывно.