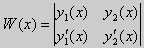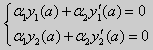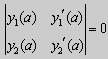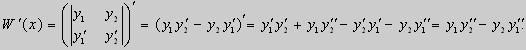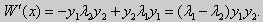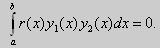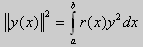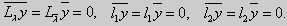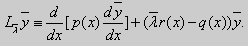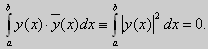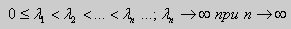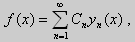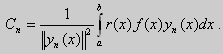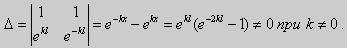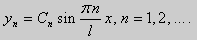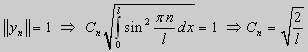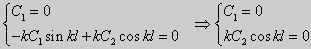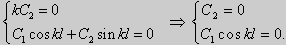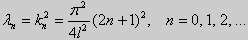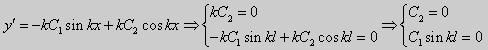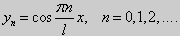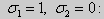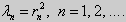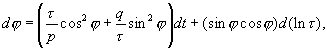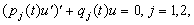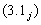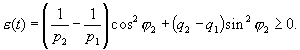Будем рассматривать однородное линейное уравнение второго порядка
Ly ≡ a2(x)y» + a1(x)y’ + a0(x)y = 0. Его можно записать по-другому:
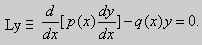 | (15) |
Однородное уравнение Ly = 0 и неоднородное Ly = f, как известно, имеют бесконечное множество решений. На практике часто бывает нужно из множества решений выделить только одно. Для этого задают некоторые дополнительные условия. Если это начальные условия у(х0) = уo, y'(xo) = y1, то получают задачу Коши. Если задают дополнительные условия на концах некоторого отрезка, то получают задачу, которая называется краевой задачей. Условия, которые задаются на концах отрезка, называются краевыми условиями. Краевые условия иногда именуют также граничными условиями и тогда говорят о граничной задаче.
Мы будем задавать линейные краевые условия вида
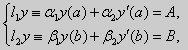 | (16) |
где α1, α2, β1, β2, A, B — заданные числа, причем по крайней мере одно из чисел α1, α2, и одно из чисел β1, β2, отличны от нуля. Если в (16) хотя бы одно из чисел А и В не равно нулю, то краевые условия называют неоднородными. Если А = В = 0, то условия (16) называются однородными. Краевая задача называется однородной, если рассматривается однородное уравнение (15) Ly = 0 и однородные краевые условия (16). Решением краевой задачи называется такое решение дифференциального уравнения, которое удовлетворяет заданным краевым условиям. Заметим сразу, что однородная краевая задача всегда имеет решение у ≡ 0 (тривиальное решение).
Наряду с уравнением (15) рассмотрим уравнение
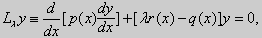 | (17) |
содержащее некоторый числовой параметр λ. Здесь функции р(х), q(x), r(x) действительные, а число λ может быть, вообще говоря, и комплексным. Краевая задача (17), (16) при А = В = 0 является однородной. Поэтому при любых λ она имеет тривиальное решение. Нас будут интересовать такие значения λ, при которых эта задача обладает не только тривиальными решениями.
Задача Штурма-Лиувилля. Найти те значения параметра λ, при которых уравнение (17) имеет нетривиальное решение, удовлетворяюшее однородным краевым условиям (16). В дальнейшем будем ее записывать в виде
<Lλy = 0, l1y = 0, l2y = 0>.
Те значения параметра λ, при которых задача Штурма-Лиувилля имеет ненулевое решение, называются собственными значениями (собственными числами) задачи, а сами эти решения — собственными функциями. Задачу Штурма-Лиувилля называют также задачей на собственные значения. В силу однородности уравнения и краевых условий собственные функции задачи Штурма-Лиувилля определены с точностью до постоянного множителя. Это означает, что если y(х) -собственная функция при некотором значении λ, то произведение Cy(x), где С — произвольная постоянная, также является собственной функцией при том же значении параметра λ. В связи с этим часто в качестве собственной функции рассматривают нормированную функцию у <х), у которой ||у(х)|| = 1. Такая собственная функция определена, по существу, однозначно (с точностью до знака ±). Далее мы подробно изучим наиболее простой случай задачи Штурма-Лиувилля, когда уравнение имеет вид
| y» + λy = 0. | (18) |
Из множества краевых условий вида (16) ограничимся тремя частными случаями:
1) краевые условия первого рода
| y(a) = y(b) = 0, | (19) |
2) краевые условия второго рода
| y'(a) = y'(b) = 0, | (20) |
3) краевые условия третьего рода
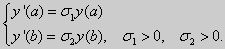 | (21) |
Общая задача Штурма-Лиувилля будет обладать свойствами, очень похожими на свойства в этих простых случаях, если на коэффициенты уравнения (17) наложить дополнительные условия: р(х), q(x), f(x) -непрерывные функции, причем р(х) имеет, кроме того, непрерывную производную на [а, b], р(х) > 0, q(x) ≥ 0.
Основные свойства собственных значений и собственных функций задачи Штурма-Лиувилля.
Лемма. Определитель Вронского двух собственных функций задачи Штурма-Лиувилля на концах отрезка [а, b] равен нулю.
Доказательство. Напомним, что определителем Вронского функций у = y1(x) и у = у2(x) называется определитель вида
Рассмотрим однородные краевые условия общего вида (16). Пусть у1(x) и у2(x) — две любые собственные функции. Это означает, что в точке x = а выполняются равенства
Числа α1, и α2 не могут одновременно равняться нулю. Значит, алгебраическая система двух однородных уравнений с двумя неизвестными имеет ненулевое решение. Это возможно только в том случае, когда определитель этой системы равен нулю:
Этот определитель совпадает с определителем Вронского в точке x = а, то есть W(a) = 0.
Аналогичные рассуждения, проведенные для точки x = b, показывают, что W(b) = 0.
Свойство 1. Две собственные функции задачи Штурма-Лиувилля, соответствующие одному и тому же собственному значению λ, линейно зависимые.
Доказательство. Так как собственные функции являются решениями одного и того же однородного уравнения (17) (по условию число λ одно), то в случае их линейной независимости определитель Вронского не равен нулю ни в одной точке отрезка [а, b]. Это противоречит только что доказанной лемме. Следовательно, y1(x) и у2(x) — линейно зависимые функции.
Свойство 2. Две собственные функции у1(x) и у2(x), соответствующие различным собственным значениям λ1 и λ2 (λ1 ≠ λ2), на отрезке [а, b] ортогональны.
Доказательство этого свойства проведем для собственных функций такой задачи, в которой уравнение имеет вид (18). Составим определитель Вронского функций у1 и у2 и продифференцируем его:
Так как у1 и у2 — решения уравнения (18) при λ = λ1 и λ = λ2, соответственно, то получим
Проинтегрируем по отрезку [а, b] левую и правую части полученного равенства. С учетом леммы будем иметь
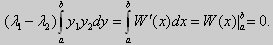
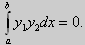
Функции y1(x) 0 и у2(х) 0, поэтому 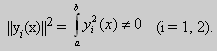
Значит, y1(x) и у2(х) на отрезке [а, b] ортогональны.
Если уравнение, входящее в задачу Штурма-Лиувилля, имеет вид (17), где r(х) > 0 и r(x) 1, то под ортогональностью функций в этом случае подразумевают ортогональность с весом r(х): две функции y1(x) и у2(х) ортогональны на отрезке [а, b] с весом r(x), если
Под нормой функции ||у(x)|| в этом случае также подразумевают весовую норму:
Свойство 3. Собственные функции, соответствующие различным собственным значениям, образуют линейно независимую систему функций.
Это утверждение вытекает из попарной ортогональности собственных функций, соответствующих различным собственным значениям (см. свойство 2).
Свойство 4. Собственные значения задачи Штурма-Лиувилля действительные.
Доказательство. Предположим, что задача Штурма-Лиувилля <Lλy = 0, l1y = 0, l2y = 0> имеет комплексное собственное значение λ = α + βi,β ≠ 0. Пусть ему соответствует собственная функция у(х) (вообще говоря, тоже комплекснозначная). Так как все коэффициенты уравнения и краевых условий имеют действительные значения, то
Здесь черта означает переход к комплексно сопряженному выражению. В нашем случае
Значит число 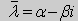
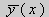
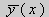
Отсюда следует, что у(x) ≡ 0 на [а, b]. Значит ни одно комплексное число λ не может быть собственным значением.
Свойство 5. Пусть коэффициенты уравнения (17) удовлетворяют условиям: р(х), q(x), r(x) — непрерывные функции и, кроме того, р(х) имеет непрерывную производную на [а, b], р(х) > 0, q(x) > 0, r(х) > 0. Тогда задача Штурма-Лиувилля <Lλ y = 0, l1 y = 0, l2 y = 0> имеет бесконечное число собственных значений λ 1, λ2, . λn, . Если краевые условия имеют вид (19) или (20), или (21), то собственные значения соответствующей задачи Штурма-Лиувилля удовлетворяют неравенствам
Теорема Стеклова.Всякая непрерывная функция f(x), удовлетворяющая однородным краевым условиям : l1f = 0 и l2f = 0 , и имеющая непрерывные производные до второго порядка на отрезке [а, b], разлагается на этом отрезке в сходящийся ряд Фурье по собственным функциям yn(х) задачи Штурма-Лиувилля <Lλ y = 0, l1 y = 0, l2 y = 0> :
где коэффициенты Фурье Сn вычисляются по формулам:
Эта теорема применяется при решении уравнений математической физики методом Фурье.
Решение задач Штурма-Лиувилля
Вначале рассмотрим уравнение (18) y» + λy = 0. и краевые условия первого рода (19) y(a) = y(b) = 0. Для удобства будем считать, что a = 0 и b = l > 0. К такой задаче можно всегда свести данную задачу, если сделать замену переменной x’ = x — a, при этом вид уравнения не изменится.
Вид общего решения уравнения (18) зависит от значений параметра λ. Разберем три случая: 1) λ 0. В первом случае обозначим λ = — k 2 . Тогда характеристическое уравнение r 2 — k 2 = 0 будет иметь действительные различные корни r1 = k, r2 = — k: Поэтому, общее решение дифференциального уравнения запишется в виде y = C1e kx + C2e -kx . Подставим краевые условия в общее решение и получим
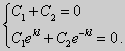
Следовательно, система имеет только нулевое (тривиальное) решение C1 = C2 = 0. Значит, при λ 2 и получим характеристическое уравнение r 2 + k 2 = 0. Оно имеет комплексные корни r1 = ki и r2 = -ki и общее решение дифференциального уравнения в этом случае запишется в виде y = C1cos kx + C2sin kx. Подставим краевые условия в общее решение:
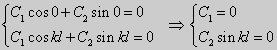 | (22) |
Для того, чтобы эта система имела нетривиальные решения, необходимо и достаточно, чтобы sin kl = 0. Следовательно kl = πn, то есть 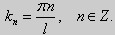
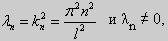
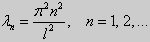
Обычно постоянный множитель выбирают либо равным единице, либо из условия нормировки:
По тому же алгоритму решаются задачи Штурма-Лиувилля следующего вида:
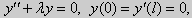 | (23) |
и
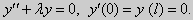 | (24) |
Эти задачи так же, как и предыдущая, при λ 0 не имеют собственных значений. В случае λ > 0 общее решение уравнения записывается в виде y = C1cos kx +C2sin kx, где 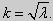
а) для задачи (23)
Для того, чтобы эти системы уравнений имели нетривиальные решения, необходимо и достаточно, чтобы coskl = 0. Следовательно, 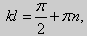
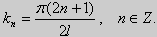
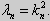
Собственные функции задачи (23) имеют вид 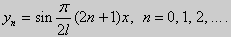
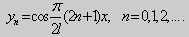 |
Некоторые отличия возникают при решении задачи Штурма-Лиувилля в случае краевых условий второго рода
| y» + λy = 0, y'(0) = y'(l) = 0. | (25) |
Рассуждениями, аналогичными тем, которые проводились для краевых условий первого рода, можно показать, что задача (25) при λ 0. В этом случае, общее решение уравнения имеет вид y = C1cos kx + C2sin kx, 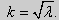
Эта алгебраическая система имеет нетривиальные решения тогда и только тогда, когда, sinkl = 0 то есть kl = πn или 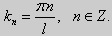
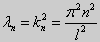
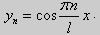
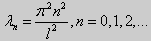
Для задачи Штурма-Лиувилля с краевыми условиями третьего рода (21) уже не удается получить собственные значения в явном виде. В качестве примера рассмотрим одну такую задачу, когда
| y» + λy = 0, y'(0) = y(0), y'(l) = 0. | (26) |
При 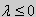
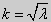
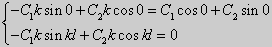
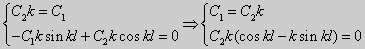 | (27) |
Получившаяся алгебраическая система будет иметь нетривиальные решения только в том случае, когда
coskl — ksinkl = 0 или
| ctgkl = k | (28) |
Уравнение (28) является трансцендентным уравнением относительно k. Оно не решается в явном виде. Однако, построив графики левой и правой частей уравнения (28), видно, что оно имеет бесконечно много решений (см. рис.13). Обозначим корни уравнения (28) через rn, n = 1,2, . . Тогда 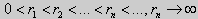
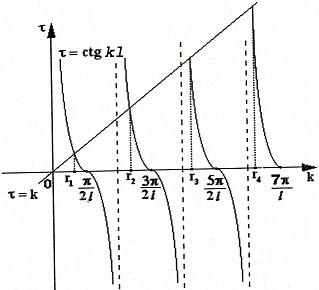
Рис.13
Численными методами можно найти приближенные значения rn. Из системы (27) при k = rn получим C1n = rnC2n , где C2n -произвольные постоянные. При этих значениях постоянных решения дифференциального уравнения будут иметь вид
Они являются собственными функциями краевой задачи (26) с собственными значениями
Видео:Сергеев И. Н. - Дифференциальные уравнения - Теорема об альтернативеСкачать

ШТУРМА ТЕОРЕМЫ
ШТУРМА ТЕОРЕМЫ — теоремы о нулях решений линейных дифференциальных уравнений 2-го порядка. Пусть у1 (х) и у2 (х) — линейно-независимые решения уравнения y”+q (х) у=0. Если х1 , х2 — последовательные нули у1 (х), то у2 (х) имеет в точности один нуль между х1 и х2. Очень важной является так называемая теорема сравнения, которая состоит в следующем: даны два уравнения: у”+q1(x)=0, z”+q2 (х) z=0 и q2 (х) ≥ q1 (х) в интервале (a, b); тогда между двумя нулями любого решения у1 (х) первого уравнения содержится хотя бы один нуль каждого решения z1(х) второго уравнения. Штурма теоремы применяются при исследовании собственных значений (см.) задачи Штурма — Лиувилля (см.) — уравнения y”+ q (х) у=λ у с однородными граничными условиями.
Видео:3. Теорема ШтурмаСкачать

Теоремы Штурма
§1. Предварительные сведения……………………………………5
Тема дипломной работы “Теорема Штурма”, связана с именем французского математика Жака Шарля Франсуа Штурма.
Штурм Жак Шарль Франсуа (Sturm J. Ch. F. – правильное произношение: Стюрм), родился 29 сентября 1803 года в Женеве. Был членом Парижской академии наук с 1836, а также иностранным членом – корреспондентом Петербургской академии наук с того же года. С 1840 года был профессором Политехнической школы в Париже.
Штурм (1824/25) и Раабе (1827) ввели главные формулы сферической тригонометрии при помощи пространственных координат.
Теорему Фурье ( Теорема о числе действительных корней между двумя данными пределами ), математика Жозефа Фурье (Joseph Fourier, 1768-1830), затмила более общая теорема, опубликованная Штурмом в Bull. mathem., 1829. Доказательство сам Штурм представил только в одной премированной работе 1835г. Коши Огюстен (Cauchy Augustin, 1789-1857) распространил теорему Штурма на комплексные корни (1831). Дополнение к ней дал также Сильвестр Джемс Джозеф (Sylvester Y.Y., 1814-1897) в 1839 году и позже.
Основные работы Жана Шарля Штурма относятся к решению краевых задач уравнений математической физики и связанной с этим задачей о разыскивании собственных значений и собственных функций для обыкновенных дифференциальных уравнений. (Задача Штурма-Лиувилля, о нахождении отличных от нуля решений дифференциальных уравнений :
удовлетворяющих граничным условиям вида:
(так называемых собственных функций), а также о нахождении значений параметра l (собственных значений), при которых существуют такие решения. При некоторых условиях на коэффициенты p(t), q(t) задача Штурма-Лиувилля сводилась к рассмотрению аналогичной задачи для уравнения вида: -u¢¢+q(x)u=lu).
Эта задача была впервые исследована Штурмом и Жозефом Лиувиллем (Joseph Liouville, 1809-1882) в 1837г. и закончена в 1841 г.
Также Жак Штурм дал общий метод для определения числа корней алгебраических уравнений, лежащих на заданном отрезке, названный правилом Штурма, который позволяет находить непересекающиеся интервалы, содержащие каждый по одному действительному корню данного алгебраического многочлена с действительными коэффициентами (уже упоминалось выше).
Ему принадлежат ряд работ по оптике и механике.
Штурм Жак Шарль Франсуа умер 18 декабря 1855года.
§ 1. Предварительные сведения
Среди дифференциальных уравнений, наиболее часто используемых в математике и физике, следует выделить линейное уравнение второго порядка, имеющее вид
(р (t) и»)» + q (f) и = h(t) . (1.2)
Как правило, если не оговорено противное, предполагается, что функции (t), g (f), h (f) и р (f) №0, q (t), входящие в эти уравнения, являются непрерывными (вещественными или комплексными) на некотором t -интервале J , который может быть как ограниченным, так и неограниченным. Причина, по которой предполагается, что р(t)№ 0, скоро станет ясной.
Из двух выражений (1.1) и (1.2) последнее является более общим, поскольку уравнение (1.1) может быть записано в виде
(p(t) и»)» + р(t) f(t)u= р (t) h (t), (1.3)
если определить p(t) следующим образом:
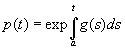
при некотором a?J. Частичное обращение этого утверждения также верно, поскольку если функция р(t) непрерывно дифференцируема, уравнение (1.2) можно записать в виде
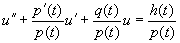
а это уравнение имеет вид (1.1).
В случае, если функция р (t) непрерывна, но не имеет непрерывной производной, уравнение (1.2) не может быть записано в виде (1.1). Тогда уравнение (1.2) можно интерпретировать как линейную систему из двух уравнений первого порядка для неизвестного двумерного вектора 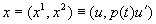

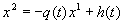
Другими словами, решение и = и (t) уравнения (1.2) должно быть такойнепрерывно дифференцируемой функцией, что функция р(t) u»(t) имеет непрерывную производную, удовлетворяющую (1.2). Если р(t) № 0 и q(t), h(t) непрерывны, к системе (1.5), а потому и к уравнению (1.2) применимы стандартные теоремы существования и единственности для линейных систем (Мы можем рассматривать также более общие (т. е. менее гладкие) типы решений, если предполагать, например, только, что функции 1/ p(t), q (t), h (t) локально интегрируемы.)
Частному случаю уравнения (1.2) при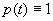
Если функция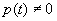
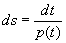

при некотором a ? J. Функция s = s (t) имеет производную 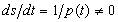

где аргумент t выражений p(f)q(t) и p(t) h(f) должен быть заменен функцией t = t(s). Уравнение (1.8) является уравнением типа (1.6).
Если функция g (t) имеет непрерывную производную, то уравнение (1.1) может быть приведено к виду (1.6) с помощью замены неизвестной функции и на z :

при некотором a ? J. В самом деле, подстановка (1.9) в (1.1) приводит к уравнению
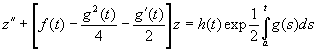
которое имеет вид (1.6).
В силу сказанного выше, мы можем считать, что рассматриваемые уравнения второго порядка в общем случае имеют вид (1.2) или (1.6). Утверждения, содержащиеся в следующих упражнениях, будут часто использоваться в дальнейшем.
§ 2. Основные факты
Прежде чем перейти к рассмотрению специальных вопросов, мы получим следствия, касающиеся однородного и неоднородного уравнений

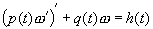
Для этого перепишем скалярные уравнения (2.1) или (2.2) в виде системы двух уравнений
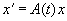
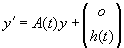
где векторы х= (х 1 , х 2 ), у == (у 1 , y 2 ) совпадают с векторами 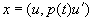
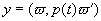
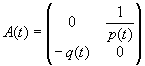
Если не оговорено противное, то предполагается, что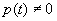
(i) Если 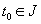
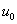
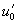
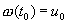
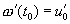
имеет единственное решение, существующее при всех 
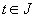
(ii) В частном случае (2.1) уравнения (2.2) и при


(iii) Принцип суперпозиции. Если 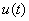
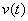
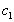
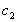
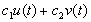
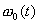

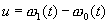
(iv) Если 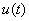

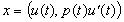
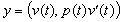
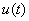
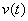
независимы в том смысле, что равенство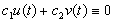
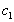
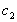
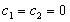
(v) Если 
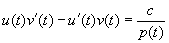
Поскольку матричным решением системы (2.3) является
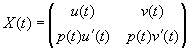
det X(t)=p(t)W(t) и trA( t )=0.
(vi) Тождество Лагранжа. Рассмотрим пару уравнений
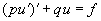

где f=f(t), g = g (t) — непрерывные функции на J. Если умножить второе уравнение на и, первое-на v и результаты вычесть, мы получим, что

так как 

где 
(vii) В частности, из (v) следует, что и(t) и v(t) — линейно независимые решения уравнения (2.1) тогда и только тогда, когда в (2.7) 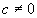
(viii) Если
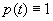
(ix) В соответствии с результатами общей теории, в случае, когда известно одно решение 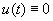




а после интегрирования мы будем иметь
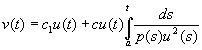
где а, 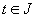
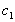
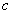
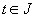
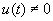
(х) Пусть и(t), v(t) — решения уравнения (2.1), удовлетворяющие (2.7) с 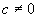
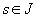

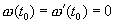

(проще проверить это непосредственно). Общее решение уравнения (2.2) получается прибавлением к (2.13) общего решения 

Если замкнутый ограниченный интервал [a,b] содержится в J, то, полагая
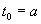
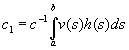
мы получаем из (2.14) частное решение

Оно может быть записано в виде
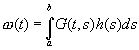
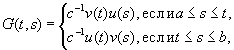
матрица С (t) зависит от 
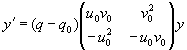
(xii) Если известно частное решение
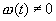
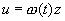
Функция z удовлетворяет дифференциальному уравнению

Умножая его на 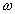
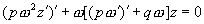
или, в силу (2.27), что
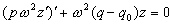
т. е. подстановка (2.29) приводит уравнение (2.1) к (2.30) или к (2.31). Мы могли также начинать не с решения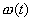

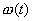
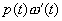
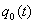
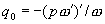
(xiii) Подстановка Лиувилля. В качестве частного случая рассмотрим (2.1) с р (t) = 1:
и» + q (t) и = 0. (2.32)
Предположим, что функция q (t) имеет непрерывную производную второго порядка, вещественна и не равна нулю, так что
±q (t) > 0, где ± = sgn q (t) (2.33)
не зависит от t. Рассмотрим вариацию постоянных
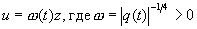
Тогда (2.32) сводится к (2.30), где
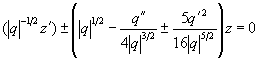
Замена независимых переменных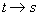
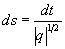
переводит (2.35) в уравнение
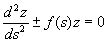
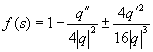
а аргументом функции q и ее производных служит функция t = t (s), обратная к функции s = s ( f), определяемой из (2.36) с помощью квадратуры; см. (1.7). В этих формулах штрих означает дифференцирование по t , так что q» = dqldt.
Замена переменных (2.34), (2.36) называется подстановкой Лиувилля. Эта подстановка, или повторное применение ее, часто приводит к дифференциальному уравнению типа (2.37), в котором функция f (s) “близка” к постоянной. Простой предельный случай такой подстановки см. в упр. 1.1(с).
(xiv) Уравнения Риккати. В п. (xi), (xii) и (xiii) рассматривались преобразования уравнения (2.1) в различные линейные уравнения второго порядка или в соответствующие линейные системы двух уравнений первого порядка.Иногда удобно преобразовать (2.1) в соответствующее нелинейное уравнение или систему. Для этого чаще всего используется следующий метод. Пусть
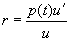
так что 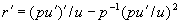
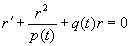
Это уравнение называется уравнением Риккати , соответствующим (2.1). (В общем случае уравнение вида 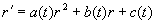
Читателю предоставляется проверка того факта, что если и (t) — решение уравнения (2.1), не равное нулю на t — интервале 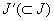

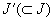
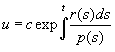
уравнения (2.1), не равное нулю ни в одной точке из J».
(xv) Преобразование Прюфера. В случае, когда уравнение (2.1) имеет вещественные коэффициенты, часто используется следующее преобразование . Пусть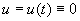
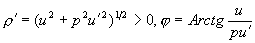
Поскольку и и и» не могут обратиться в нуль одновременно, то, фиксируя соответствующее значение функции 

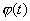
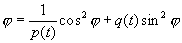
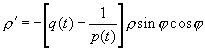
В уравнение (2.43) входит лишь одна из неизвестных функций
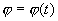
Преимущество уравнения (2.43) по сравнению с (2.40) состоит в том, что всякое решение уравнения (2.43) существует на всем интервале J, где непрерывны р и q. Это видно из соотношения, связывающего решения уравнений (2.1) и (2.43).
Упражнение 2.1 . Проверьте, что если функция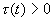
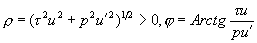
при фиксированном значении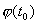
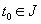
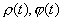
Соотношения (2.46) и (2.47) следует понимать так, что интегралы Римана — Стильтьеса от обеих их частей равны. Обратно, (непрерывные) решения системы уравнений (2.46), (2.47) определяют решения уравнения (2.1) с помощью соотношений (2.45). Заметим, что если q (t) > 0, р (t) > 0 и функция q(t) р ( t ) имеет локально ограниченную вариацию, то, полагая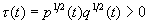



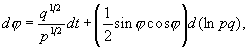
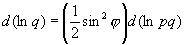
§ 3. Теоремы Штурма
В этом параграфе мы будем рассматривать только уравнение вида (2.1) с вещественными непрерывными коэффициентами р (t) > 0, q (t). Под “решением” мы будем понимать “вещественное, нетривиальное (т. е. 
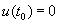
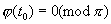
Лемма 3.1. Пусть 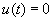

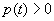

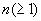
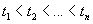
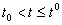
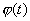
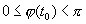
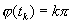
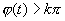
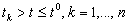
Доказательство. Заметим, что в той точке t, где u=0 , т. е. где 
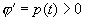
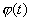
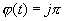
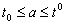
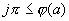
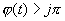
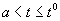
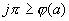
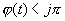
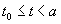
В теоремах этого параграфа будут рассматриваться два уравнения
где функции 
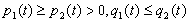
В этом случае уравнение (3.1) называется мажорантой Штурма для (3.1) на J, а уравнение (3.1) -минорантой Штурма для (3.1). Если дополнительно известно, что соотношения
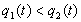
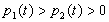
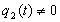
выполняются в некоторой точке 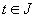
Теорема 3.1 (первая теорема сравнения Штурма). Пусть коэффициенты уравнения 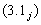
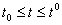
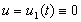
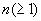
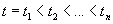
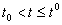
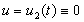
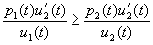
при 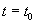
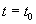
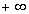
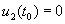

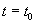
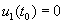
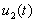

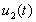
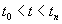

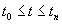
Доказательство. В силу (3.4) можно определить при 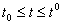
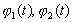
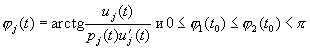
Тогда справедливы аналоги соотношения (2.43):
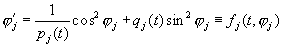
Поскольку непрерывные функции 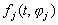
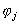
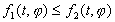
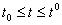

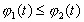
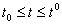
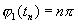
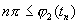
Чтобы доказать последнюю часть теоремы, предположим вначале, что при 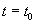
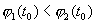
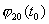
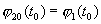
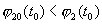
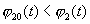


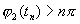
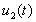
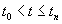
Рассмотрим теперь тот случай, когда в (3.4) имеет место равенство, но в некоторой точке из 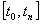
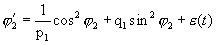
Если доказываемое утверждение неверно, то из уже рассмотренного случая следует, что 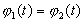
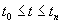
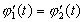
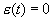
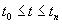
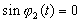


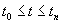
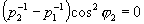
Следовательно, если 
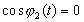

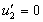
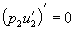
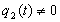
Следствие 3.1 (теорема Штурма о разделении нулей). Пусть уравнение (3.1 2 ) является мажорантой Штурма для (3.1 1 ) на интервале J, и пусть 


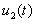

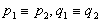

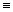
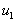
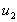
Заметим, что, последнее утверждение этой теоремы имеет смысл, поскольку нули функций 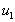
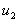
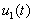


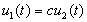
Упражнение 3.1 . (Другое доказательство теоремы Штурма о разделении нулей, когда p 1 (t)ºp 2 (t)>0, q 2 (t)³q 1 (t).)
Предположим, что u 1 (t)>0 при t 1 2 3 и утверждение неверно: например, u 2 (t)>0 при t 1£ t£t 2 . Умножая (p 1 (t)u¢)¢+q 1 (t)u=0, где u=u 1 , на u 2 , а (p 2 (t)u¢)¢+q 2 (t)u=0, где u=u 2 , на u 1 , вычитая и интегрируя по [t 1, t 2 ], получаем:
p(t)(u 1¢ u 2 -u 1 u 2¢ )³0, при t 1£ t£t 2 , где p=p 1 =p 2 . Это означает, что (u 1 /u 2 )¢³0; поэтому u 1 /u 2 >0 при t 1 2 , т.е. получается, что u 1 (t 2 )>0 чего быть не может.
(p 1 (t)u¢)¢+q 1 (t)u=0, u=u 1
(p 1 (t)u 1¢ )¢+q 1 (t)u 1 =0.
Умножим левую часть равенства на u 2 , получим:
u 2 (p 1 (t)u 1¢ )¢+q 1 (t)u 1 u 2 =0.
Во втором уравнении проделаем соответствующие операции:
(p 2 (t)u¢)¢+q 2 (t)u=0, u 2 =u
(p 2 (t)u 2¢ )¢+q 2 (t)u 2 =0.
Умножим левую часть равенства на u 1 , получим:
u 1 (p 2 (t)u 2¢ )¢+q 2 (t)u 1 u 2 =0.
Вычитаем из первого уравнения второе, получим:
u 2 (p 1 u 1¢ )¢+q 1 u 1 u 2 -u 1 (p 2 u 2¢ )¢-q 2 u 1 u 2 =0, p=p 1 =p 2
u 2 (pu 1¢ )¢+q 1 u 1 u 2 -u 1 (pu 2¢ )¢-q 2 u 1 u 2 =0
(u 2 (pu 1¢ )¢-u 1 (pu 2¢ )¢)+u 1 u 2 (q 1 -q 2 )=0
Упростим это уравнение,
u 2 (p¢u 1¢ +pu 1¢¢ )-u 1 (p¢u 2¢ +pu 2¢¢ )+u 1 u 2 (q 1 -q 2 )=0
Раскроем скобки, получим:
p¢u 1¢ u 2 + pu 1¢¢ u 2 — p¢u 1 u 2¢ -pu 1 u 2¢¢ +u 1 u 2 (q 1 -q 2 )=0.
Сравнивая с формулой (2.2), получаем:
(p(u 1¢ u 2 -u 1 u 2¢ ))¢+u 1 u 2 (q 1 -q 2 )=0
(p(u 1¢ u 2 -u 1 u 2¢ ))¢-u 1 u 2 (q 2 -q 1 )=0
(p(u 1¢ u 2 -u 1 u 2¢ ))¢=u 1 u 2 (q 2 -q 1 )=0.
Проинтегрируем это уравнение по [t 1 ,t], получим:


u 1 u 2 >0, q 2 -q 1³ 0. Значит p(u 1¢ u 2 -u 1 u 2¢ )³0.
Т.о. (u 1 /u 2 )¢³0 Þ u 1 /u 2 >0.
Упражнение 3.2. с) Проверьте, что вещественные решения u(t) ¹0 уравнения u¢¢+m/t 2 u=0 (1/17) имеет не более одного нуля при t>0, если m£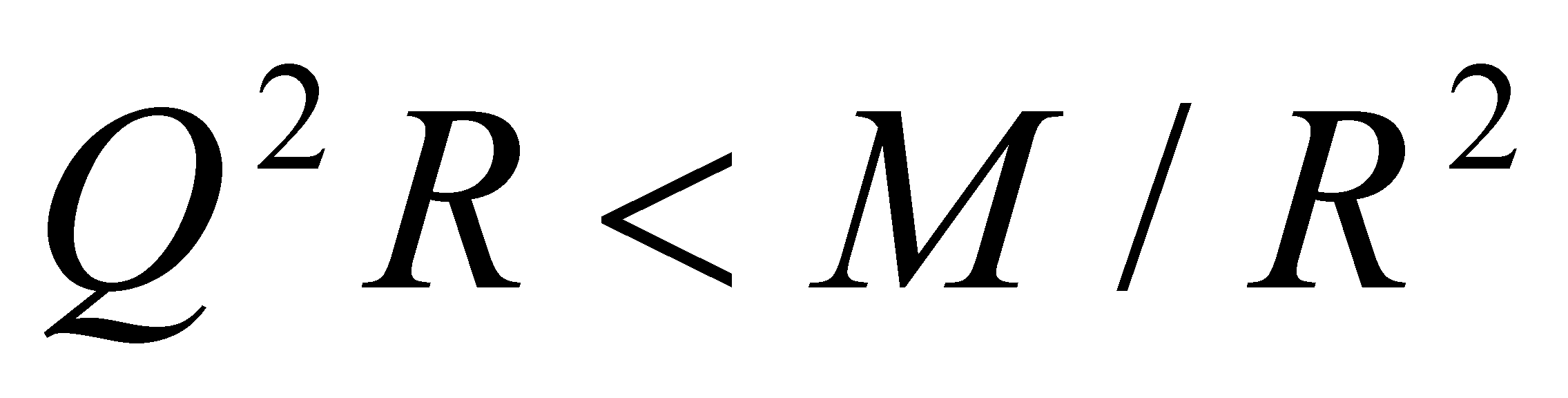
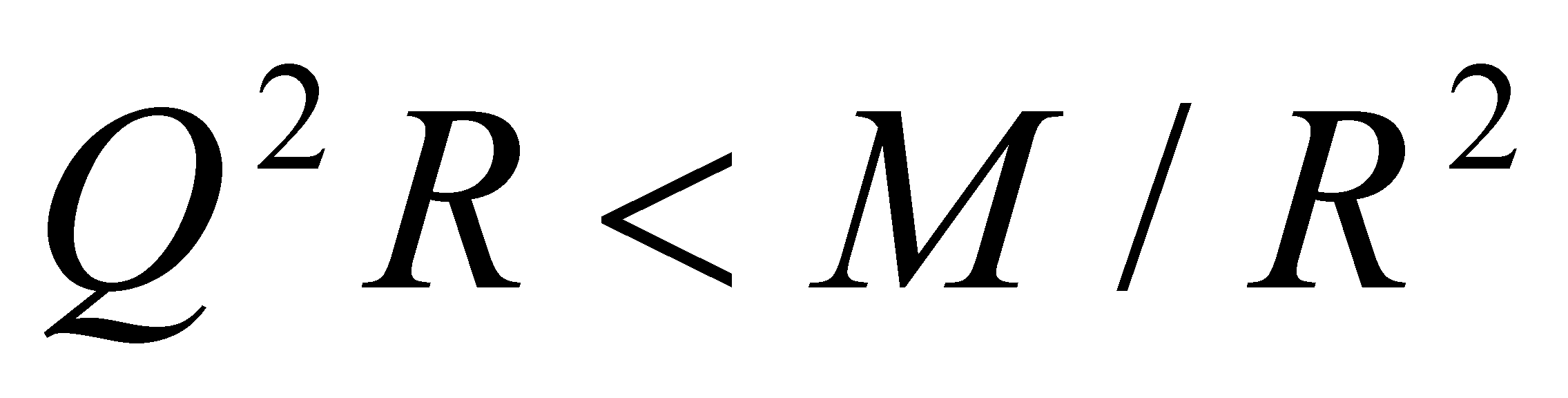
Решение: в §1 было рассмотрено упражнение 1.1 с), где показали, что функция u=tl является решением уравнения u¢¢+m/t 2 u=0 тогда и только тогда, когда l удовлетворяет уравнению l(l-1)+ m=0. Решая его получили : l=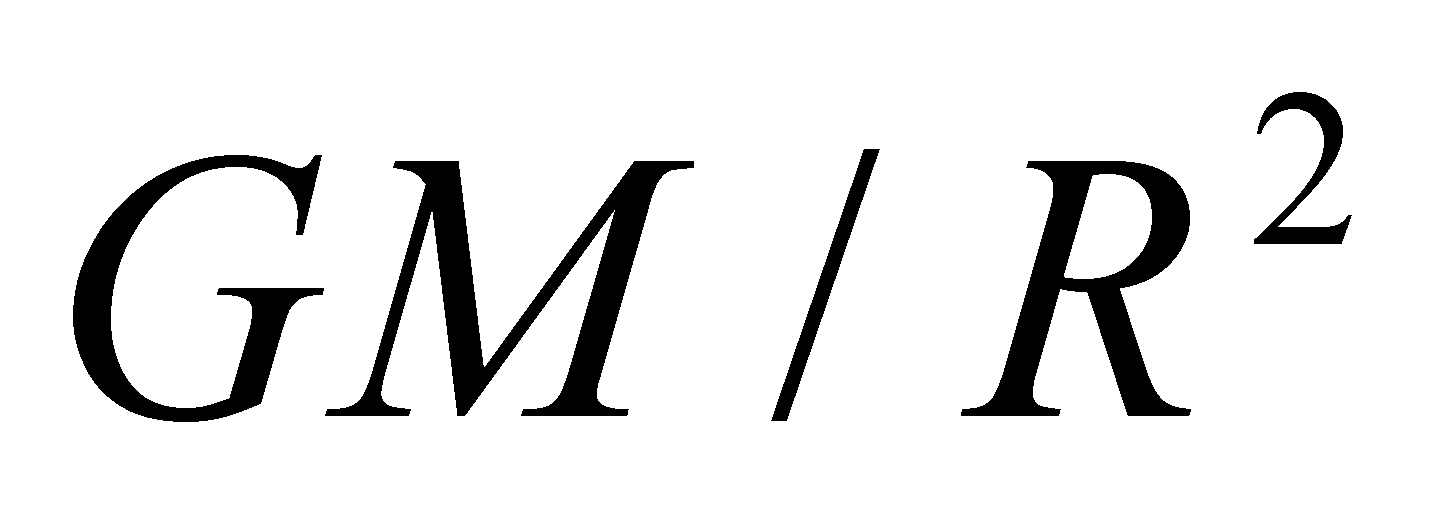
Если m>1/4, то корни l 1 и l 2 – комплексные, т.е.
u=t 1/2 [cos (

имеют бесчисленное множество нулей. В частности, если положить:
c 1 =sinu ,c 2 =cosu,
u= t 1/2 [sin u cos (

t 1/2 [sin (u+
Если m 1 t 1/2+ +c 2 t 1/2-
имеют не более одного нуля.
Так же, если m=1/4, то решение
u=c 1 t 1/2 +c 2 t 1/2 ln t
имеют не более одного нуля.
d) Рассмотрим уравнение Бесселя:
v¢¢+v¢/t+(1-m 2 /t 2 )v=0, (3.10)
где m-вещественный параметр. Вариация постоянных u=t 1/2 /v переводит уравнение (3.10) в уравнение:
u¢¢+(1-a/t 2 )u=0, где a=m 2 -1/4 (3.11)
Проверим истинность этого утверждения u=t 1/2 v, следовательно:
Найдём первую производную:
v¢=(ut -1/2 ) ¢=u¢t -1/2 +u(t -1/2 )¢=u¢t -1/2 -1/2ut -3/2 .
Теперь вторую производную:
v¢¢=(u¢t 1/2 ) ¢-1/2(ut -3/2 ) ¢=u¢¢t -1/2 +u¢(t -1/2 ) ¢-1/2(u¢t -3/2 +u(t -3/2 ) ¢)=
=u¢¢t -1/2 –1/2u¢t -3/2 -1/2u¢t -3/2 +3/4uut -5/2 =
=u¢¢t -1/2 -u¢t -3/2 +3/4ut -5/2 .
Подставляя в уравнение (3.10), получим:
u¢¢t -1/2 -u¢t -3/2 +3/4ut -5/2 +1/t(u¢t -1/2 -1/2ut -3/2 )+(1-m 2 /t 2 )ut -1/2 =0
t -1/2 (u¢¢-u¢t -1 +3/4ut -2 +u¢t -1 -1/2ut -2 +u(1-m 2 /t 2 ))=0
u¢¢+1/4ut -2 +u(1-m 2 /t 2 )=0
u¢¢+u-m 2 u/t 2 +1/4ut -2 =0
u¢¢+u-(m 2 u-1/4u)/t 2 =0
u¢¢+(1-a/t 2 )u=0, где a=m 2 -1/4.
Покажем, что нули вещественного решения v(t) уравнения (3.10) образуют при t>0 такую последовательность t 1 2 n -t n-1®p при n®¥.
Так как в уравнении
u¢¢+(1-a/t 2 )u=0, т.е. уравнение
m — постоянное число, то при m³1/4 и при t – достаточно большое, то выражение
1-(m 2 -1/4)/t 2® 1, т.е. если уравнение
сравнить с уравнением u¢¢+u=0, то расстояние между последовательными нулями стремится к p, т.е. t n -t n-1®p при n®¥.
Теорема 3.2 (вторая теорема сравнения Штурма). Пусть выполнены условия первой части теоремы 3.1 и функция 
Доказательство этого утверждения содержится по существу в доказательстве теоремы 3.1, если заметить, что из предположения о числе нулей функции 
Ф. Хартман. Обыкновенные дифференциальные уравнения: Учебн. пособие./ Пер. с англ. И.Х.Сабитова, Ю.В.Егорова; под ред. В.М.Алексеева.-М.: изд.”Мир”, 1970г.-720 с.
В.В.Степанов. Курс дифференциальных уравнений. Гос.изд. “Технико-теор. литер.”-М., 1953г.-468 с.
Большая Советская Энциклопедия. /Под ред. А.М.Прохорова. Изд. 3-е., М., “Советская Энциклопедия”, 1978г., т.29. “Чачан-Эне-ле-Бен.” – 640 с.
Г.Вилейтнер. “История математики от Декарта до середины 19-го столетия.” М., изд. “Наука.”, 1966г. – 508 с.
История математики с древнейших времён до начала 19-го столетия. /Под ред. Юшкевича А.П., т.3 /Математика 18-го столетия/., изд. “Наука.”, М., 1972г. – 496 с.
Ошибка в тексте? Выдели её мышкой и нажми
Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!
🔍 Видео
Дифференциальные уравнения 12. Теорема Штурма.Скачать

№3. Теорема Штурма. Автономные системы уравнений.Скачать

5.1 Задача Штурма-ЛиувилляСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Разбор решения задачи Штурма-ЛиувилляСкачать

Дифференциальные уравнения 19. Теорема Штурма. Критерий КнезераСкачать

Чеченский отряд и диверсия на территории России | НОВОСТИСкачать

Линейная алгебра. Алексей Савватеев и Александр Тонис. Лекция 13.4. Существов. и единств. решения ДУСкачать

Видеоурок "Системы дифференциальных уравнений"Скачать

Лукьяненко Д. В. - Дифференциальные уравнения - Лекция 2Скачать

Дифференциальные уравнения | задача Штурма - Лиувилля | классические краевые задачи | 1Скачать

Олегу Тинькову запрещён вход на Мехмат МГУСкачать

Асташова И. В. - Дифференциальные уравнения I - Теорема о продолжении решенияСкачать