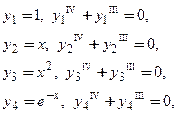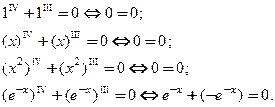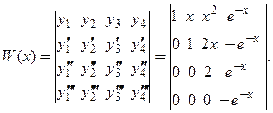Данная статья рассматривает способы решения линейных дифференциальных однородных уравнений второго порядка с постоянными коэффициентами вида y » + p y ‘ + q y = 0 с p и q являющимися действительными числами. Будет рассмотрена теория с приведением примеров с подробным решением.
Перейдем к формулировке теоремы, которая показывает, какого вида должно быть уравнение, чтобы можно было искать общее решение ЛОДУ.
- Теорема общего решения линейного однородного дифференциального уравнения
- Алгоритм нахождения общего решения линейного однородного дифференциального уравнения
- ЛИНЕЙНЫЕ ОДНОРОДНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
- Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- Основные понятия о линейных дифференциальных уравнениях второго порядка и их решениях
- Линейное однородное дифференциальное уравнение второго порядка и его решение
- Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами: теория и практика
- Решить линейное однородное дифференциальное уравнение с постоянными коэффициентами самостоятельно, а затем посмотреть решение
- 🔥 Видео
Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Теорема общего решения линейного однородного дифференциального уравнения
Общим решением линейного однородного дифференциального уравнения вида y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 0 ( x ) · y = 0 с непрерывными на интервале интегрирования x коэффициентами f 0 ( x ) , f 1 ( x ) , . . . , f n — 1 ( x ) определяют линейную комбинацию вида y 0 = ∑ j = 1 n C j · y j , где y j , j = 1 , 2 , . . . , n являются линейно независимыми частными решениями ЛОДУ на интервале x , где C j , j = 1 , 2 , . . . , n берут за произвольные постоянные.
Отсюда получаем, что общее решение такого уравнения y » + p y ‘ + q y = 0 может быть записано как y 0 = C 1 ⋅ y 1 + C 2 ⋅ y 2 , где y 1 и y 2 выражаются линейно независимыми решениями, а С 1 и C 2 – произвольными постоянными. Необходимо поработать с нахождением частных решений y 1 и y 2 .
Существует формула по Эйлеру для поиска частных решений вида y = e k · x .
Если взять y = e k · x за частное решение ЛОДУ второго порядка с постоянными коэффициентами y » + p y ‘ + q y = 0 , тогда, используя подстановку, получим тождество вида:
e k · x » + p · e k · x ‘ + q · e k · x = 0 k 2 · e k · x + p · e k · x + q · e k · x = 0 e k · x · ( k 2 + p · k + q ) = 0 k 2 + p · k + q = 0
Данное тождество называют характеристическим уравнением с постоянными коэффициентами k 1 и k 2 , которые и являются его решениями и определяют частые решения вида y 1 = e k 1 · x и y 2 = e k 2 · x заданного ЛОДУ.
При различных значениях p и q можно получить характеристические уравнения с корнами такого вида:
- Действительные и различные k 1 ≠ k 2 , k 1 , k 2 ∈ R .
- Действительные и совпадающие k 1 = k 2 , = k 0 , k 0 ∈ R .
- Комплексно сопряженную пару k 1 = α + i · β , k 2 = α — i · β .
Первый случай показывает, что решениями такого уравнения могут быть y 1 = e k 1 · x и y 2 = e k 2 · x , а общее решение принимает вид y 0 = C 1 · e k 1 · x + C 2 · e k 2 · x с постоянными коэффициентами. Функции y 1 = e k 1 · x и y 2 = e k 2 · x рассматриваются, как линейно независимыми по причине отличного от нуля определителя Вронского W ( x ) = y 1 y 2 y 1 ‘ y 2 ‘ = e k 1 · x e k 2 · x k 1 · e k 1 · x k 2 · e k 2 · x = e k 1 · x · e k 2 · x · k 2 — k 1 с действительными k 1 ≠ k 2 , k 1 , k 2 ∈ R .
Второй случай объясняет, что первым частным решением функции – это выражение y 1 = e k 0 · x . Вторым частным решением можно брать y 2 = x · e k 0 · x . Определим, что y 2 = x · e k 0 · x может являться частным решением ЛОДУ второго порядка с постоянными коэффициентами y » + p y ‘ + q y = 0 и докажем линейную независимость y 1 и y 2 .
Имеем, что k 1 = k 0 и k 2 = k 0 являются совпадающими корнями характеристического уравнения. Тогда оно примет вид k — k 0 2 = 0 ⇔ k 2 — 2 k 0 · k + k 0 2 = 0 . Отсюда следует, что y » — 2 k 0 · y ‘ + k 0 2 · y = 0 является линейным однородным дифференциальным уравнением. Необходимо подставить выражение y 2 = x · e k 0 · x для того, чтобы убедиться в тождественности:
y 2 » — 2 k 0 · y ‘ 2 + k 0 2 · y 2 = 0 x · e k 0 · x » — 2 k 0 · x · e k 0 x ‘ + k 0 2 · x · e k 0 · x = 0 e k 0 · x + k 0 · x · e k 0 x ‘ — 2 k 0 · e k 0 · x + k 0 · x · e k 0 x + k 0 2 · x · e k 0 · x = 0 ( k 0 · e k 0 · x + k 0 · e k 0 · x + k 0 2 · x · e k 0 · x — — 2 k 0 · e k 0 · x — k 0 2 · x · e k 0 · x + k 0 2 · x · e k 0 · x ) = 0 0 ≡ 0
Отсюда следует, что y 2 = x · e k 0 · x — это частное решение данного уравнения. Необходимо рассмотреть линейную независимость y 1 = e k 0 · x и y 2 = x · e k 0 · x . Чтобы убедиться в этом, следует прибегнуть к вычислению определителя Вронского. Он не должен быть равен нулю.
W ( x ) = y 1 y 2 y 1 ‘ y 2 ‘ = e k 0 · x x · e k 0 · x e k 0 · x ‘ x · e k 0 · x ‘ = = e k 0 · x x · e k 0 · x k 0 · e k 0 · x e k 0 · x · ( 1 + k 0 · x ) = = e k 0 · x · e k 0 · x · 1 + k 0 · x — k 0 · x · e k 0 · x · e k 0 · x = e 2 k 0 · x ≠ 0 ∀ x ∈ R
Можно сделать вывод, что линейно независимые частные решения ЛОДУ второго порядка с постоянными коэффициентами y » + p y ‘ + q y = 0 считаются y 1 = e k 0 · x и y 2 = x · e k 0 · x . Это подразумевает то, что решением будет являться выражение y 0 = C 1 · e k 0 · x + C 2 · x · e k 0 · x при k 1 = k 2 = k 0 , k 0 ∈ R .
Третий случай говорит о том, что имеем дело с парой комплексных частных решений ЛОДУ вида y 1 = e α + i · β · x и y 2 = e α — i · β · x .
Запись общего решения примет вид y 0 = C 1 · e α + i · β · x + C 2 · e α — i · β · x .
Функции y 1 = e a · x · cos β x и y 2 = e a · x · sin β x могут быть записаны вместо частных решений уравнения, причем с соответствующими действительной и мнимой частями. Это понятно при преобразовании общего решения y 0 = C 1 · e α + i · β · x + C 2 · e α — i · β · x . Для этого необходимо воспользоваться формулами из теории функции комплексного переменного вида. Тогда получим, что
y 0 = C 1 · e α + i · β · x + C 2 · e α — i · β · x = = C 1 · e α · x · cos β x + i · sin β x + C 2 · e α · x · cos β x — i · sin β x = = ( C 1 + C 2 ) · e α · x · cos β x + i · ( C 1 — C 2 ) · e α · x · sin β x = = C 3 · e α · x · cos β x + C 4 · e α · x · sin β x
Отчетливо видно, что С 3 и С 4 используются в качестве произвольных постоянных.
Видео:Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Скачать

Алгоритм нахождения общего решения линейного однородного дифференциального уравнения
Алгоритм нахождения общего решения линейного однородного дифференциального уравнения 2 порядка с постоянными переменными вида y » + p y ‘ + q y = 0 :
- Запись характеристического уравнения k 2 + p ⋅ k + q = 0 .
- Нахождение корней характеристического уравнения k 1 и k 2 .
- Производим запись ЛОДУ, исходя из полученных значений с постоянными коэффициентами:
- y 0 = C 1 · e k 1 · x + C 2 · e k 2 · x при k 1 ≠ k 2 , k 1 , k 2 ∈ R ;
- y 0 = C 1 · e k 0 · x + C 2 · x · e k 0 · x при k 1 = k 2 = k 0 , k 0 ∈ R ;
- y 0 = e α · x · ( C 1 · cos β x + C 2 · sin β x ) при k 1 = α + i · β , k 2 = α — i · β .
Найти общее решение заданного уравнения с постоянными коэффициентами y » + 4 y ‘ + 4 y = 0 .
Решение
Следуя алгоритму, необходимо записать характеристическое уравнение k 2 + 4 ⋅ k + 4 = 0 , после чего обозначить его корни. Получаем, что
k 2 + 4 k + 4 = 0 ( k + 2 ) 2 = 0 k 1 = k 2 = k 0 = — 2
Очевидно, что полученные корни являются совпадающими.
Ответ: Запись общего решения: y 0 = C 1 · e k 0 x + C 2 · x · e k 0 x = C 1 · e — 2 x + C 2 · x · e — 2 x .
Найти решение заданного уравнения вида y » — 5 y ‘ + 6 y = 0 .
Решение
По условию имеется ЛОДУ 2 порядка с постоянными коэффициентами. Это указывает на то, что необходимо записать характеристическое уравнение и обозначить его корни. Получим:
k 2 — 5 k + 6 = 0 D = 5 2 — 4 · 6 = 1 k 1 = 5 — 1 2 = 2 k 2 = 5 + 1 2 = 3
Видно, что корни различные и действительные. Это говорит о том, что уравнение общего вида запишется как y 0 = C 1 · e k 1 x + C 2 e k 2 x = C 1 · e 2 x + C 2 · e 3 x .
Ответ: y 0 = C 1 · e k 1 x + C 2 e k 2 x = C 1 · e 2 x + C 2 · e 3 x .
Найти общее решение дифференциального уравнения вида y » — y ‘ + 3 y = 0 .
Решение
Необходимо перейти к характеристическому уравнению ЛОДУ 2 порядка, что соответствует записи k 2 — k + 3 = 0 , после чего обозначить его корни. Тогда получим, что
D = 1 2 — 4 · 3 = — 11 k 1 = 1 + i 11 2 = 1 2 + i · 11 2 k 2 = 1 — i 11 2 = 1 2 — i · 11 2 ⇒ α = 1 2 , β = 11 2
На выходе имеем пару комплексно сопряженных корней характеристического уравнения. Отсюда следует, что общим решением является запись уравнения вида
y 0 = e a · x · ( C 1 · cos β x + C 2 · sin β x ) = = e x 2 · C 1 · cos 11 x 2 + C 2 · sin 11 2
Ответ: y 0 = e x 2 · C 1 · cos 11 x 2 + C 2 · sin 11 2 .
Видео:15. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать

ЛИНЕЙНЫЕ ОДНОРОДНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
ЛИНЕЙНЫЕ ОДНОРОДНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
N-ГО ПОРЯДКА
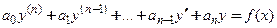
называется линейным неоднородным дифференциальным уравнением n-го порядка, если коэффициенты 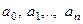
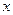
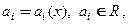
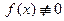
Если функция 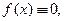
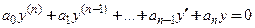
Уравнение (2) называют линейным однородным дифференциальным уравнением n-го порядка, соответствующим (отвечающим) неоднородному уравнению (1).
Свойства решений линейных однородных уравнений
1. Если 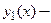
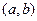
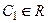
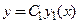
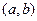
2. Если 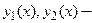
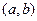
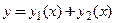
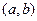
С л е д с т в и е. Если 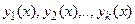
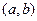
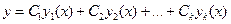
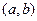
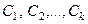
В теории линейных дифференциальных уравнений важную роль играет понятие линейной независимости системы функций на интервале.
Функции 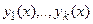
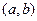
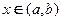
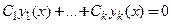
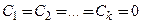
В противном случае эти функции называются линейно зависимым на 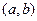
Проверку линейной независимости системы решений однородного уравнения n-го порядка удобно выполнять при помощи следующей теоремы.
Теорема 1. Чтобы решения линейного однородного уравнения n-го порядка 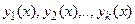
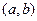
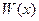
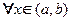
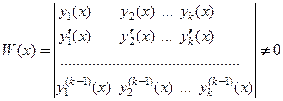
Фундаментальной системой решений линейного однородного уравненияn-го порядка на интервале 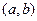
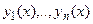
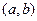
В теореме 1 сформулирован критерий фундаментальности набора (системы) n решений линейного однородного уравнения n-го порядка.
Теорема 2 (об общем решении линейного однородного уравнения). Если функции 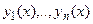
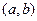
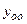
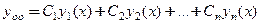
где 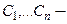
Теорема 3 (об общем решении линейного неоднородного уравнения). Если функция 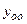
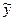
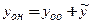
является общим решением уравнения (1).
З а м е ч а н и е (п р и н ц и п с у п е р п о з и ц и и).Если правая часть линейного неоднородного уравнения является суммой функций: 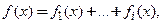
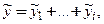
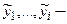
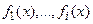
Пример 1. Проверить фундаментальность системы решений 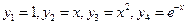
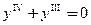
□ Непосредственной подстановкой функций 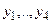
Проверим, являются ли решения уравнения 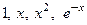
Известно, что определитель треугольной матрицы равен произведению диагональных элементов: 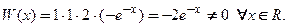
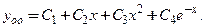
ЛИНЕЙНЫЕ ОДНОРОДНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
Рассмотрим линейное дифференциальное уравнение n-го порядка
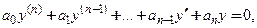
где коэффициенты 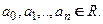
При помощи подстановки Эйлера 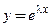
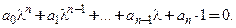
Это уравнение (7) и многочлен, корни которого следует найти, называют характеристическим уравнением и характеристическим многочленом соответственно.
Корни характеристического многочлена с действительными коэффициентами могут быть как действительными, так и комплексными числами (см. разд. 1.2.3 и 1.6.5).
Рассмотрим два случая.
1. Пусть 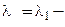
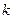
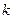
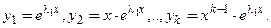
При 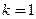
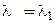
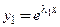
2. Пусть 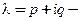
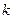
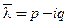
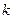
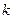
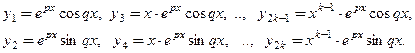
Частные решения, соответствующие разным корням характеристического уравнения (7), линейно независимы.
Как только найдено n частных линейно независимых решений, по теореме 2 можно написать общее решение в виде их линейной комбинации.
Алгоритм 1 решения линейного однородного уравнения с постоянными коэффициентами
1. Составить характеристическое уравнение (7).
2. Найти все корни уравнения (7) и определить их кратности.
3. Для каждого найденного корня написать соответствующие частные решения по
формулам (8) или (9).
4. Составить фундаментальную систему решений и записать общее решение по формуле (4).
Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Видео:16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Основные понятия о линейных дифференциальных уравнениях второго порядка и их решениях
Линейным дифференциальным уравнением второго порядка называется уравнение вида
где y — функция, которую требуется найти, а p(x) , q(x) и f(x) — непрерывные функции на некотором интервале (a, b) .
Если правая часть уравнения равна нулю ( f(x) = 0 ), то уравнение называется линейным однородным уравнением. Таким уравнениям и будет в основном посвящена практическая часть этого урока. Если же правая часть уравнения не равна нулю ( f(x) ≠ 0 ), то уравнение называется линейным неоднородным уравнением (смотрите отдельный урок).
В задачах от нас требуется разрешить уравнение относительно y» :
Линейные дифференциальные уравнения второго порядка имеют единственное решение задачи Коши.
Видео:ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Линейное однородное дифференциальное уравнение второго порядка и его решение
Рассмотрим линейное однородное дифференциальное уравнение второго порядка:
Если y 1 (x) и y 2 (x) — частные решения этого уравнения, то верны следующие высказывания:
1) y 1 (x) + y 2 (x) — также является решением этого уравнения;
2) Cy 1 (x) , где C — произвольная постоянная (константа), также является решением этого уравнения.
Из этих двух высказываний следует, что функция
также является решением этого уравнения.
Возникает справедливый вопрос: не является ли это решение общим решением линейного однородного дифференциального уравнения второго порядка, то есть таким решением, в котором при различных значениях C 1 и C 2 можно получить все возможные решения уравнения?
Ответ на этот вопрос следуюший: может, но при некотором условии. Это условие о том, какими свойствами должны обладать частные решения y 1 (x) и y 2 (x) .
И это условие называется условием линейной независимости частных решений.
Теорема. Функция C 1 y 1 (x) + C 2 y 2 (x) является общим решением линейного однородного дифференциального уравнения второго порядка, если функции y 1 (x) и y 2 (x) линейно независимы.
Определение. Функции y 1 (x) и y 2 (x) называются линейно независимыми, если их отношение является константой, отличной от нуля:
Однако установить по определению, являются ли эти функции линейно независимыми, часто очень трудоёмко. Существует способ установления линейной независимости с помощью определителя Вронского W(x) :

Если определитель Вронского не равен нулю, то решения — линейно независимые. Если определитель Вронского равен нулю, то решения — линейно зависимымые.
Пример 1. Найти общее решение линейного однородного дифференциального уравнения 
Решение. Интегрируем дважды и, как легко заметить, чтобы разность второй производной функции и самой функции была равна нулю, решения должны быть связаны с экспонентой, производная которой равна ей самой. То есть частными решениями являются 

Так как определитель Вронского
не равен нулю, то эти решения линейно независимы. Следовательно, общее решение данного уравнения можно записать в виде

Видео:Теорема о структуре общего решения линейного однородного дифференциального уравненияСкачать

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами: теория и практика
Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида
где p и q — постоянные величины.
На то, что это уравнение второго порядка, указывает наличие второй производной от искомой функции, а на его однородность — нуль в правой части. Постоянными коэффициентами называются уже упомянутые выше величины.
Чтобы решить линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами, нужно сначала решить так называемое характеристическое уравнение вида
которое, как видно, является обычным квадратным уравнением.
В зависимости от решения характеристического уравнения возможны три различных варианта решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами, которые сейчас разберём. Для полной определённости будем считать, что все частные решения прошли проверку определителем Вронского и он во всех случаях не равен нулю. Сомневающиеся, впрочем, могут проверить это самостоятельно.
Корни характеристического уравнения — действительные и различные
Иными словами, 

Пример 2. Решить линейное однородное дифференциальное уравнение

Решение. Характеристическое уравнение имеет вид 





Пример 3. Решить линейное однородное дифференциальное уравнение

Решение. Характеристическое уравнение имеет вид 





Корни характеристического уравения — вещественные и равные
То есть, 

Пример 4. Решить линейное однородное дифференциальное уравнение

Решение. Характеристическое уравнение 



Пример 5. Решить линейное однородное дифференциальное уравнение

Решение. Характеристическое уравнение 




Корни характеристического уравнения — комплексные
То есть, 



Пример 6. Решить линейное однородное дифференциальное уравнение

Решение. Характеристическое уравнение 





Пример 7. Решить линейное однородное дифференциальное уравнение

Решение. Характеристическое уравнение 





Решить линейное однородное дифференциальное уравнение с постоянными коэффициентами самостоятельно, а затем посмотреть решение
Пример 8. Решить линейное однородное дифференциальное уравнение

Пример 9. Решить линейное однородное дифференциальное уравнение

🔥 Видео
Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

Линейное дифференциальное уравнение Коши-ЭйлераСкачать

Решение линейного однородного дифференциального уравнения. Практическая часть. 11 класс.Скачать

Однородное линейное дифференциальное уравнение. Алгоритм решенияСкачать

Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентамСкачать

19. Общее решение линейного уравненияСкачать

Теорема об общем решении ЛОДУ второго порядка. (Дифференциальные уравнения - урок 12)Скачать

Теорема об общем решении ЛНДУ второго порядка. (Дифференциальные уравнения - урок 14)Скачать

14. Дифференциальные уравнения второго порядка, допускающие понижение порядкаСкачать

Дифференциальные уравнения, 8 урок, Линейные дифференциальные уравнения с const коэф-ами 2 порядкаСкачать

13. Как решить дифференциальное уравнение первого порядка?Скачать

4. Однородные дифференциальные уравнения (часть 1)Скачать