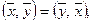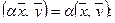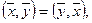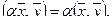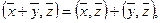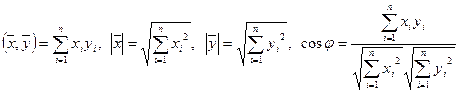Рассмотрим систему m линейных алгебраических уравнений относительно n неизвестных 
Определение. Решением системы называется совокупность n значений неизвестных 
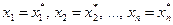
Определение. Система, имеющая хотя бы одно решение, называется совместной; система, не имеющая ни одного решения — несовместной.
Напомним, что система линейных уравнений может быть записана в матричной форме:

где 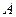
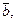

Необходимое и достаточное условие совместности системы линейных алгебраических уравнений
На вопрос о совместности системы линейных алгебраических уравнений отвечает следующая теорема.
Теорема (теорема Кронекера-Капелли). Для того, чтобы неоднородная система линейных алгебраических уравнений была совместна, необходимо и достаточно, чтобы ранг расширенной матрицы системы совпадал с рангом матрицы системы.
Доказательство теоремы.
Необходимость. Система 

Система 

т.е. вектор-столбец правой части линейно выражается через столбцы 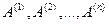
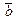

Достаточность. 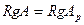
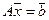
Пусть 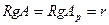
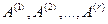
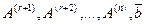

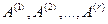
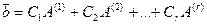
Положим 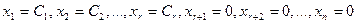
т.е. вектор 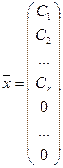

т.е. система 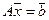
Свойства решений систем линейных алгебраических уравнений
Используя свойства линейных операций с матрицами, нетрудно доказать, справедливость следующих утверждений.
1. Если 
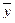
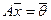
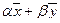
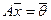
2. Если 
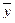

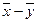
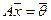
3. Если 

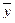
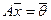


Докажем, например, первое из этих свойств. Пусть 
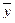
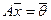
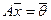
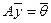
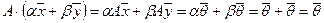
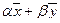
Остальные утверждения докажите аналогично самостоятельно.
Структура общего решения неоднородной системы
Вспомним одно из свойств решений линейной неоднородной системы:
Если 
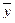

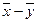
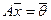
Поскольку выражение 

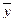
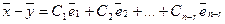
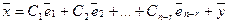
Таким образом доказана теорема о структуре общего решения линейной неоднородной системы.
Теорема о структуре общего решения неоднородной системы линейных алгебраических уравнений. Если ранг r матрицы неоднородной системы линейных уравнений меньше числа неизвестных n , то общее решение системы можно записать в виде
где 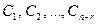
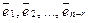
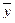
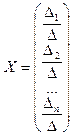
Формулы Крамера. Рассмотрим систему n линейных алгебраических уравнений относительно n неизвестных
Обозначим: 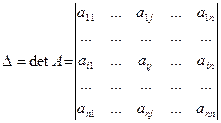
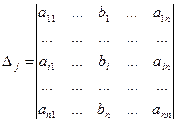
Если определитель матрицы системы отличен от нуля, 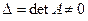
определяется равенствами: 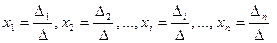
Докажем это утверждение. Пусть 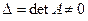
Обозначим 
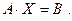
Вычислим определитель 
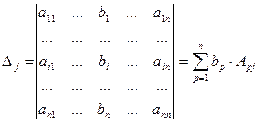
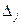
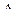
Т.е. 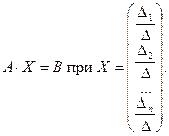
Замечание. Нетрудно, показать, что выражения 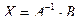
Действительно,
Лекция 6. Линейное пространство. Линейная зависимость системы векторов. Размерность, базис. Линейное подпространство. Примеры
Линейное пространство арифметических векторов R n
Определение. Арифметическим вектором называется упорядоченная совокупность n чисел. Обозначается 
Для арифметических векторов определены линейные операции — сложение арифметических векторов и умножение вектора на число: 
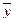
Определение. Множество арифметических векторов, для которых определены операции сложения и умножения на число называется пространством арифметических векторов R n .
Вектор 

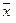
Для любых 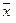
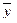
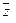
1. 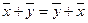
2. 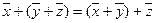
3.
4.
5. 
6. 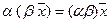
7. 
8.
Примерами пространства арифметических векторов являются пространства геометрических векторов на плоскости, записанных в координатной форме.
Линейная зависимость и линейная независимость в R n
Определение. Линейной комбинацией векторов 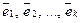
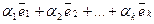
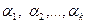
Определение. Говорят, что вектор 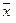
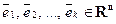
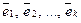
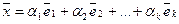
Определение. Система 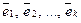
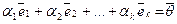
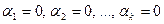
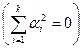
Иными словами, линейная комбинация векторов равна нулю тогда и только тогда, когда все коэффициенты линейной комбинации равны нулю.
Определение. Система векторов, которая не является линейно зависимой, называется линейно независимой.
Иными словами, существуют такие коэффициенты линейной комбинации 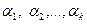

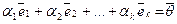
Или: линейная комбинация векторов может обратиться в нуль, хотя не все коэффициенты линейной комбинации равны нулю.
Пример. Исследуем на линейную зависимость векторы 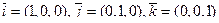
Составим линейную комбинацию векторов и приравняем ее нулю:
Т.е. линейная комбинация равна нулю тогда и только тогда, когда все ее коэффициенты нулевые — векторы 
Пример. Исследуем на линейную зависимость систему векторов 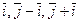
Составим линейную комбинацию векторов и приравняем ее нулю:
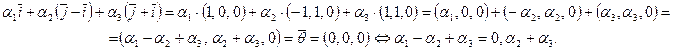
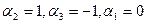
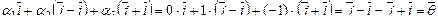
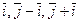
Свойства линейно зависимых и линейно независимых систем функций
1. Любая система векторов, содержащая нулевой вектор линейно зависима.
2. Любая система векторов, содержащая пару взаимно противоположных векторов — линейно зависима.
3. Любая система векторов, содержащая два равные вектора — линейно зависима.
4. Любая подсистема линейно независимой системы векторов — линейно независима.
5. Если некоторая подсистема системы векторов линейно зависима, то и вся система — линейно зависима.
Докажем первое из этих утверждений: любая система векторов, содержащая нулевой вектор линейно зависима. Рассмотрим произвольную систему векторов 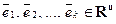
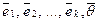
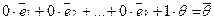
Остальные утверждения доказываются аналогично. Докажите сами.
Необходимое и достаточное условие линейной зависимости системы векторов в R n
Справедливо следующее утверждение.
Теорема (Необходимое и достаточное условие линейной зависимости системы векторов). Система 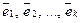
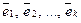
Доказательство теоремы. Необходимость. Дано: векторы 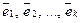
Векторы 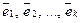
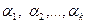
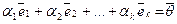
Не умаляя общности, предположим, что именно 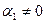
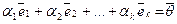
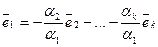
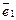
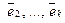
Достаточность. Дано: один из векторов системы 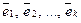
Действительно, не умаляя общности, положим, что вектор 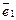
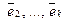
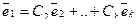




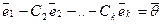
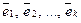
Базис в R n . Координаты вектора в заданном базисе. Линейные операции в координатной форме
Определение. Система векторов из R n образует базис в R n если:
1. система векторов упорядочена;
2. система векторов линейно независима;
3. любой вектор из R n линейно выражается через векторы системы.
Иными словами, линейно независимая упорядоченная система векторов
Образует базис в R n если любой вектор 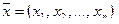


Определение. Выражение 
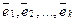
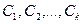
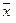
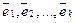
Пример. Нетрудно доказать, что система арифметических векторов
линейно независима (см. пример с 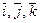
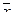
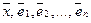
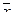
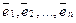


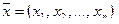
Справедливо следующее утверждение.
Теорема (о единственности разложения вектора в базисе). Для любого вектора 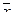

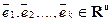
Доказательство теоремы. «От противного». Пусть не так. Т.е. векторы 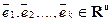

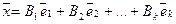
Тогда 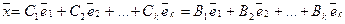
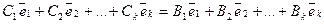
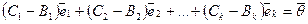
Но векторы 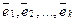
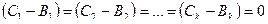

Следствие. Координаты вектора в заданном базисе определяются единственным образом.
Теорема. В пространстве R n существует базис из n векторов.
Действительно, этот базис — естественный базис
Линейные операции в координатной форме
Пусть векторы 
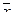
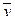

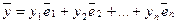

для любого числа 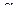
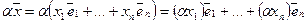
Иными словами, координаты суммы векторов в заданном базисе равны сумме соответствующих координат слагаемых, а координаты произведения вектора на число — произведению соответствующих координат вектора на число.
Линейные подпространства в R n , размерность подпространства, базис в подпространстве
Определение. Множество L векторов из R n , такое, что для любых 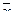
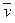
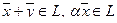
Пример. Множество L арифметических векторов из R n , у которых последние компоненты — нулевые, образует линейное подпространство в R n :
Нетрудно доказать, что для любого линейного подпространства справедливо:
- если вектор
принадлежит линейному подпространству L, то и вектор
принадлежит линейному подпространству L;
- любое линейное подпространство содержит нулевой элемент.
Действительно, пусть 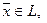
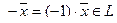

Утверждение. Пространство R n само является линейным подпространством в R n .
Это утверждение очевидно, поскольку сумма любых двух векторов из R n и произведение любого вектора из R n на любое число принадлежат R n .
Определение. Число k называется размерностью линейного подпространства L , если в L существует система из k линейно независимых векторов, а любые k +1 вектора — линейно зависимы. Обозначаем dimL = k .
Нетрудно доказать следующее утверждение.
Теорема. В k -мерном линейном подпространстве существует базис их k векторов.
Доказательство теоремы. Действительно, если dimL = k, то существует система из k линейно независимых векторов 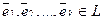

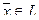

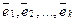
Справедливы также следующие утверждения (оставим их без доказательства).
Теорема. Любая упорядоченная система из k линейно независимых векторов k -мерного линейного подпространства является базисом в этом подпространстве.
Теорема. Размерность линейного подпространства равна числу векторов в базисе этого подпространства.
Отсюда следует: dim ( R n ) = n.
Действительно, в пространстве R n есть базис из n векторов — естественный базис в R n .
Пример. Размерность линейного подпространства L арифметических векторов из R n , у которых последние компоненты — нулевые, равна n – 1.
Действительно, векторы 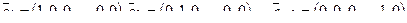
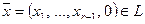

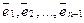
Тогда можно использовать другое определение базиса.
Определение. Любая упорядоченная линейно независимая система из k векторов k -мерного линейного подпространства L образует базис этого линейного подпространства L .
Это означает, что если dimL = k и арифметические векторы 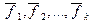
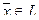
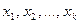
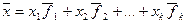
Метрические соотношения в R n
Определение. Если каждой паре векторов 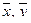
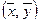
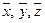
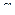
1.
2.
3.
4. 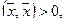
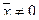
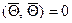
то говорят, что в пространстве R n определено скалярное произведение 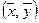
Пример. Легко проверить, что изученное в разделе «аналитическая геометрия» скалярное произведение известное из школьного курса скалярное произведение в трехмерном пространстве геометрических векторов (в R 3 ) является скалярным произведением в определенном выше смысле.
Пример. Рассмотрим пространство арифметических векторов R 2 =<X=(x1, x2)>. Определим скалярное произведение следующим образом:
Легко убедиться, что для определенного таким образом скалярного произведения справедливы аксиомы 1. — 4.:
(X , X) = 2x1x1 + 3x2x2 = 2x1 2 + 3x2 2 >0 если 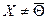
Вернемся к пространству арифметических векторов R n = < 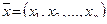
Определим в R n естественное скалярное произведение: каждой паре векторов 
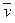
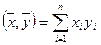
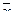
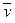
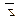
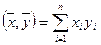
1.
2.
3.
4. 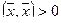
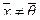
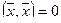
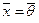
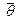
Пространство арифметических векторов R n с определенным в нем естественным скалярным произведением называют евклидовым пространством арифметических векторов и иногда обозначают E n .
Свойства скалярного произведения. Неравенство Коши-Буняковского
Теорема (неравенство Коши-Буняковского). Для любых векторов 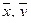
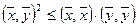
Доказательство теоремы. Возьмем произвольное число 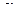
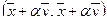
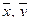
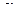
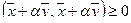
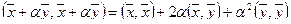

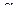

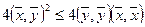

Метрические соотношения в R n
Определение. Число 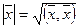

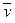

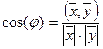
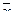
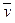
Если в R n скалярное произведение определено формулой 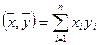
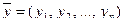
Ортогональность, ортогональные системы, ортонормированные базисы
Определение. Векторы 
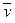
Определение. Система 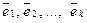
Теорема (о линейной независимости ортогональных систем). Ортогональная система векторов линейно независима.
Доказательство теоремы.
Предположим противное: векторы 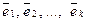


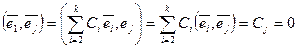
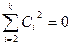
Определение. Система 
Определение. Базис пространства R n называется ортонормированным базисом, если образующие его векторы попарно ортогональны и имеют единичную длину.
В пространстве R n в естественном скалярном произведении 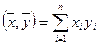
Подпространство строк и подпространство столбцов прямоугольной матрицы
Рассмотрим прямоугольную матрицу Am , n, у которой m строк и n столбцов:
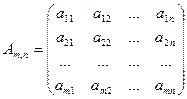
Её строки — 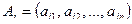
А столбцы — 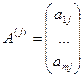
Понятно, что множество строк матрицы Am , n , к которому добавили все строки, которые могут быть получены при элементарных преобразованиях матрицы (исключая транспонирование) — линейное подпространство в R n .
А аналогично образованное множество столбцов — линейное подпространство в R m .
Это означает, что мы можем говорить о линейной зависимости и о линейной независимости строк и столбцов матрицы, о размерности подпространства строк и подпространства столбцов матрицы, о базисах в соответствующих подпространствах.
- Теорема о структуре общего решения неоднородной системы линейных алгебраических уравнений
- Теорема о структуре общего решения неоднородной системы линейных алгебраических уравнений
- Структура общего решения системы уравнений
- Свойства решений однородной системы уравнений
- Алгоритм решения однородной системы уравнений
- Структура общего решения неоднородной системы уравнений
- Свойства решений неоднородной системы уравнений
- Алгоритм решения неоднородной системы уравнений
- 📸 Видео
Видео:Неоднородная система линейных уравненийСкачать

Теорема о структуре общего решения неоднородной системы линейных алгебраических уравнений
достаточно найти общее решение однородной системы уравнений
и частное решение неоднородной системы уравнений (*).
Сумма этих решений представляет собой общее решение неоднородной системы уравнений (*).
В плане практического применения такой метод решения неоднородных систем линейных уравнений не слишком распространен. Однако подход подобного рода является весьма эффективным применительно к решению линейных неоднородных дифференциальных уравнений.
| AX = B | (1) |
может быть представлено в виде суммы общего решения соответствующей однородной системы
| AX = 0 | (2) |
и любого частного решения неоднородной системы (1).
Доказательство. Пусть матрица X 0 является общим решением однородной системы (2):
| AX 0 = 0. | (3) |
Обозначим символическим выражением X ч частное решение неоднородной системы (1):
| AXч = B. | (4) |
Складывая тождества (3) и (4), получам тождество
| A ( X0 + Xч ) = B, | (5) |
справедливое при любых значениях свободных параметров, входящих в общее решение X0 .
Следовательно, матрица X0 + Xч является общим решением матричного уравнения (1).
Видео:Теорема о структуре общего решения однородной системы линейных уравненийСкачать

Теорема о структуре общего решения неоднородной системы линейных алгебраических уравнений
Пусть задана неоднородная система линейных алгебраических уравнений размерности m × n .
Матрица 

Исследование любой системы линейных алгебраических уравнений начинается с преобразования ее расширенной матрицы методом Гаусса , который основан на следующих элементарных преобразованиях:
– перестановка строк матрицы;
– умножение строк матрицы на действительное отличное от руля число;
– поэлементное сложение строк матрицы;
– вычеркивание нулевой строки;
– транспонирование матрицы (в этом случае преобразования производятся по столбцам).
Элементарные преобразования приводят первоначальную систему к системе, ей эквивалентной. Системы называются эквивалентными, если они имеют одно и то же множество решений.
Рангом матрицы называется наивысший порядок отличных от нуля ее миноров. Элементарные преобразования ранга матрицы не меняют.
На вопрос о наличии решений у неоднородной системы линейных уравнений отвечает следующая теорема.
Теорема 1.3 (теорема Кронекера-Капелли). Неоднородная система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу ее главной матрицы, то есть
Обозначим количество строк, оставшихся в матрице после метода Гаусса, через r (соответственно, в системе остается r уравнений). Эти строки матрицы называются базисными.
Если r = n , то система имеет единственное решение (является совместной определенной), ее матрица элементарными преобразованиями приводится к треугольному виду. Такую систему можно решить также методом Крамера и с помощью обратной матрицы .
Если r n (количество переменных в системе больше количеств а уравнений), матрица элементарными преобразованиями приводится к ступенчатому виду. Такая система имеет множество решений и является совместной неопределенной. В данном случае для нахождения решений системы необходимо выполнить ряд операций.
1. Оставить в левых частях уравнений системы r неизвестных (базисные переменные), остальные n — r неизвестных перенести в правые части (свободные переменные). После разделения переменных на базисные и свободные система принимает вид:
2. Из коэффициентов при базисных переменных составить минор (базисный минор), который должен быть отличен от нуля.
3. Если базисный минор системы (1.10) равен нулю, то одну из базисных переменных следует заменить на свободную; полученный базисный минор снова проверить на отличие от нуля.
4. Применяя формулы (1.6) метода Крамера, считая правые части уравнений их свободными членами, найти выражение базисных переменных через свободные в общем виде. Полученный при этом упорядоченный набор переменных системы является ее общим решением.
5. Придавая свободным переменным в (1.10) произвольные значения, вычислить соответствующие значения базисных переменных. Получаемый при этом упорядоченный набор значений всех переменных называется частным решением системы, соответствующим данным значениям свободных переменных. Система имеет бесконечное множество частных решений.
6. Получить базисное решение системы – частное решение, получаемое при нулевых значениях свободных переменных.
Заметим, что количество базисных наборов переменных системы (1.10) равно числу сочетаний из n элементов по r элементов Cn r . Так как каждому базисному набору переменных соответствует свое базисное решение, следовательно, количество базисных решений у системы также равно Cn r .
Пусть строки матрицы обозначены соответственно l 1 ; l 2 ;…; ln . Строка l называется линейной комбинацией строк l 1 ; l 2 ;…; ln матрицы, если она равна сумме произведений этих строк на произвольные действительные числа, то есть , 
Однородная система уравнений всегда совместна, так как имеет хотя бы одно – нулевое (тривиальное) решение. Для того чтобы однородная система n линейных уравнений с n переменными имела ненулевые решения, необходимо и достаточно, чтобы ее главный определитель ∆ был равен нулю. Это означает, что ранг r ее главной матрицы меньше числа n неизвестных ( r n ) . В этом случае исследование однородной системы уравнений на общее и частные решения проводится аналогично исследованию неоднородной системы. Решения однородной системы уравнений обладают важным свойством: если известны два различных решения однородной системы линейных алгебраических уравнений, то их линейная комбинация также является решением этой системы. Нетрудно убедиться в справедливости следующей теоремы.
Теорема 1.4. Общее решение неоднородной системы уравнений представляет собой сумму общего решения соответствующей однородной системы и некоторого частного решения неоднородной системы уравнений
Пример 1.7. Исследовать заданную систему уравнений и найти одно частное решение:
Решение. Выпишем расширенную матрицу системы и применим к ней элементарные преобразования:
Так как r ( A ) =2 и 



По формулам (1.6) имеем
Данное выражение базисных переменных через свободные представляет собой общее решение системы:
При конкретных значениях свободных переменных из общего решения получаем частное решение системы. Например, частное решение 
Видео:Лекция 13. Исследование систем линейных уравнений. Теорема Кронекера — Капелли.Скачать

Структура общего решения системы уравнений
Однородная система линейных уравнений
всегда совместна, так как имеет тривиальное решение . Если ранг матрицы системы равен количеству неизвестных , то тривиальное решение единственное. Предположим, что . Тогда однородная система имеет бесконечно много решений. Заметим, что расширенная матрица однородной системы при элементарных преобразованиях строк приводится к упрощенному виду , т.е. . Поэтому из (5.11) получаем общее решение однородной системы уравнений :
Получим другую форму записи решений однородной системы, которая раскрывает структуру множества решений. Для этого подчеркнем следующие свойства.
Видео:Теорема о структуре общего решения линейного неоднородного дифференциального уравненияСкачать

Свойства решений однородной системы уравнений
1. Если столбцы — решения однородной системы уравнений, то любая их линейная комбинация также является решением однородной системы.
В самом деле, из равенств следует, что
т.е. линейная комбинация решений является решением однородной системы.
2. Если ранг матрицы однородной системы равен , то система имеет линейно независимых решений.
Действительно, по формулам (5.13) общего решения однородной системы найдем частных решений , придавая свободным переменным следующие стандартные наборы значений (всякий раз полагая, что одна из свободных переменных равна единице, а остальные — равны нулю):
которые линейно независимы. В самом деле, если из этих столбцов составить матрицу, то последние ее строк образуют единичную матрицу. Следовательно, минор, расположенный в последних строках не равен нулю (он равен единице), т.е. является базисным. Поэтому ранг матрицы будет равен . Значит, все столбцы этой матрицы линейно независимы (см. теорему 3.4).
Любая совокупность линейно независимых решений однородной системы называется фундаментальной системой (совокупностью) решений .
Заметим, что фундаментальная система решений определяется неоднозначно. Однородная система может иметь разные фундаментальные системы решений, состоящие из одного и того же количества линейно независимых решений.
Теорема 5.3 об общем решении однородной системы. Если — фундаментальная система решений однородной системы уравнений (5.4), то столбец
при любых значениях произвольных постоянных также является решением системы (5.4), и, наоборот, для каждого решения х этой системы найдутся такие значения произвольных постоянных , при которых это решение удовлетворяет равенству (5.14).
Прямое утверждение теоремы следует из свойства 1 решений однородной системы. Докажем обратное утверждение о том, что любое решение можно представить в виде (5.14). Для этого составим матрицу , приписав к столбцам фундаментальной системы решений столбец
Найдем ранг этой матрицы. Так как первые столбцов линейно независимы, то . Так как каждый из столбцов матрицы является решением системы , то по первой формуле из (5.13) получаем
Следовательно, первая строка матрицы является линейной комбинацией последних строк этой матрицы.
По второй формуле из (5.13) получим, что вторая строка матрицы является линейной комбинацией последних строк этой матрицы, и т.д. По r-й формуле из (5.13) получим, что r-я строка матрицы является линейной комбинацией последних строк этой матрицы. Значит, первые строк матрицы можно вычеркнуть и при этом ранг матрицы не изменится. Следовательно, , так как после вычеркивания в матрице будет всего строк. Таким образом, . Значит, есть базисный минор матрицы , который расположен в первых ее столбцах, а столбец не входит в этот базисный минор. Тогда по теореме о базисном миноре найдутся такие числа , что
Итак, обратное утверждение доказано.
Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Алгоритм решения однородной системы уравнений
1-5. Выполнить первые 5 пунктов алгоритма Гаусса. При этом не требуется выяснять совместность системы, так как любая однородная система имеет решение (пункт 3 метода Гаусса следует пропустить). Получить формулы (5.11) общего решения, которые для однородной системы будут иметь вид (5.13).
Если ранг матрицы системы равен числу неизвестных , то система имеет единственное тривиальное решение и процесс решения заканчивается.
Если ранг матрицы системы меньше числа неизвестных , то система имеет бесконечно много решений. Структуру множества решений находим в следующих пунктах алгоритма.
6. Найти фундаментальную систему решений однородной системы. Для этого подставить в (5.13) последовательно стандартных наборов значений свободных переменных, в которых все свободные переменные равны нулю, кроме одной, равной единице (см. свойство 2 решений однородной системы).
7. Записать общее решение однородной системы по формуле (5.14).
1. В пункте 6 алгоритма вместо стандартного набора значений свободных переменных можно использовать и другие наборы значений, лишь бы они обеспечивали линейную независимость получаемых частных решений однородной системы.
2. Матрица столбцы которой образуют фундаментальную систему решений однородной системы, называется фундаментальной. Используя фундаментальную матрицу, общее решение (5.14) однородной системы можно записать в виде
3. Если базисный минор матрицы расположен в левом верхнем углу (в первых строках и первых столбцах), то упрощенный вид расширенной матрицы (5.9) однородной системы можно представить в виде блочной матрицы
Тогда блочная матрица размеров является фундаментальной. В этом можно убедиться, используя стандартные наборы значений свободных переменных. Применение блочных матриц может служить вторым способом нахождения фундаментальной системы решений.
Пример 5.4. Найти фундаментальную систему решений и общее решение однородной системы
Решение. 1. Составляем расширенную матрицу системы
2-4. Используя элементарные преобразования над строками матрицы , приводим ее к ступенчатому, а затем и к упрощенному виду (см. решение примера 5.3):
Пункт 3 метода Гаусса пропускаем.
5. Переменные — базисные, а — свободные. Записываем формулу (5.13) общего решения однородной системы
6. Находим фундаментальную систему решений. Так как и , надо подобрать линейно независимых решения. Подставляем в систему стандартные наборы значений свободных переменных:
В результате получили фундаментальную систему решений
7. Записываем общее решение однородной системы по формуле (5.14):
Заметим, что фундаментальную систему решений можно получить, взяв иные наборы значений свободных переменных. Например, и . Тогда получим другую фундаментальную систему решений
Несмотря на различия, обе формулы задают одно и то же множество решений.
Видео:Теорема о структуре общего решения линейного однородного дифференциального уравненияСкачать

Структура общего решения неоднородной системы уравнений
Ранее была выведена формула (5.11) общего решения системы линейных уравнений. Получим другую форму записи, отражающую структуру множества решений.
Рассмотрим неоднородную систему и соответствующую ей однородную систему . Между решениями этих систем имеются связи, выражающиеся следующими свойствами.
Видео:Лекция 15. Критерий Кронекера-Капелли. Общее решение однородной и неоднородной СЛАУ. Примеры.Скачать

Свойства решений неоднородной системы уравнений
1. Разность двух решений и неоднородной системы есть решение однородной системы.
Действительно, из равенств и следует, что .
2. Пусть — решение неоднородной системы. Тогда любое решение неоднородной системы можно представить в виде
В самом деле, для любого решения неоднородной системы разность по свойству 1 является решением однородной системы, т.е. — решение однородной системы.
Теорема 5.4 о структуре общего решения неоднородной системы.
Пусть — решение неоднородной системы, а — фундаментальная система решений соответствующей однородной системы уравнений. Тогда столбец
при любых значениях [i]произвольных постоянных является решением неоднородной системы, и, наоборот, для каждого решения этой системы найдутся такие значения произвольных постоянных , при которых это решение удовлетворяет равенству (5.15).[/i]
Говорят, что общее решение неоднородной системы есть сумма частного решения неоднородной системы и общего решения соответствующей однородной системы.
Доказательство теоремы вытекает из свойств 1, 2 и теоремы 5.3.
Видео:Теорема Кронекера-КапеллиСкачать

Алгоритм решения неоднородной системы уравнений
1-5. Выполнить первые 5 пунктов метода Гаусса решения системы уравнений и получить формулу общего решения неоднородной системы вида (5.11).
6. Найти частное решение неоднородной системы, положив в (5.11) все свободные переменные равными нулю.
7. Записав формулы (5.13) общего решения соответствующей однородной системы, составить фундаментальную систему ее решений. Для этого подставить в (5.13) последовательно стандартных наборов значений свободных переменных, в которых все переменные равны нулю, за исключением одной, равной единице.
8. Записать общее решение неоднородной системы по формуле (5.15).
1. Используя фундаментальную матрицу однородной системы , решение неоднородной системы можно представить в виде
2. Если базисный минор матрицы расположен в левом верхнем углу (в первых строках и первых столбцах), то упрощенный вид расширенной матрицы (5.9) неоднородной системы можно представить в виде блочной матрицы
Тогда блочная матрица оказывается фундаментальной (см. п.3 замечаний 5.3), а столбец является частным решением неоднородной системы (в этом можно убедиться, подставляя в (5.11) нулевой набор свободных переменных). Используя блочные матрицы, общее решение (5 15) неоднородной системы можно представить в виде
где — столбец произвольных постоянных. Полученную формулу можно считать вторым способом решения неоднородной системы.
Пример 5.5. Найти структуру (5.15) общего решения неоднородной системы
Решение. 1-5. Первые 5 пунктов метода Гаусса выполнены при решении примера 5.3, где получены формулы общего решения неоднородной системы:
Переменные — базисные, а — свободные.
6. Полагая , получаем частное решение неоднородной системы .
7. Находим фундаментальную систему решений однородной системы (см. пример 5.4):
8. Записываем по формуле (5.15) общее решение неоднородной системы
Искомая структура множества решений найдена.
Получим формулу общего решения вторым способом , используя п.2 замечаний 5.4. При решении примера 5.3 расширенная матрица системы была приведена к упрощенному виду. Разбиваем ее на блоки:
Записываем частное решение неоднородной системы
и составляем фундаментальную матрицу:
По формуле (5.16) получаем общее решение неоднородной системы, которое преобразуем к виду (5.15):
📸 Видео
Математика без Ху!ни. Метод Гаусса.Скачать

Неоднородные системы линейных уравненийСкачать
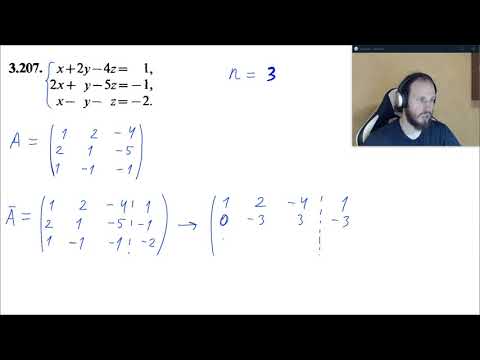
Система линейных уравнений. Общее решение. Метод ГауссаСкачать

ФСР. Система однородных уравнений. Общее решениеСкачать

Видеоурок "Однородные системы линейных уравнений"Скачать

Решение неоднородных линейных систем. ТемаСкачать

Решение системы уравнений методом ГауссаСкачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

СЛАУ: Фундаментальная система решений. Структура общего решения | Лекция 7 | ЛинАл | СтримСкачать

Системы линейных уравнений: Теорема Кронекера-КапеллиСкачать

Лекция 14. Системы линейных алгебраических уравнений.Скачать

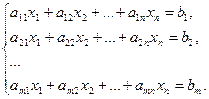
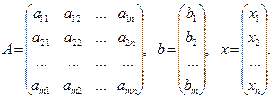
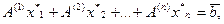

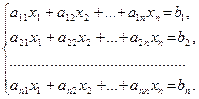
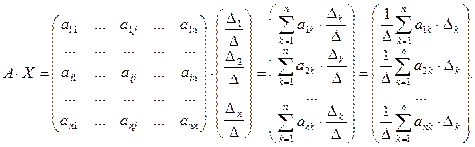
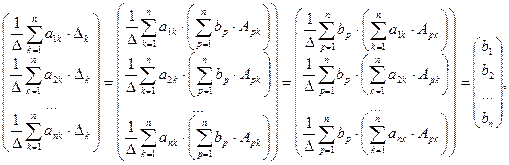
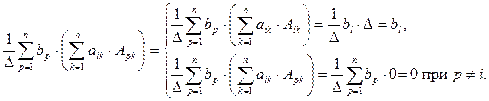
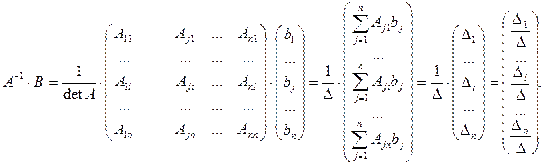
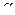

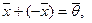
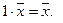

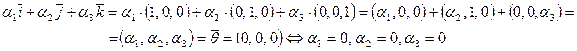
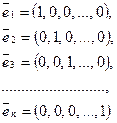
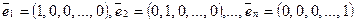
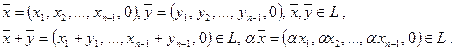
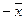 принадлежит линейному подпространству L;
принадлежит линейному подпространству L;