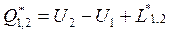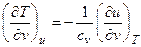В инженерных расчетах часто пользуются уравнением состояния идеального газа с введением в него поправочного коэффициента (z), называемого коэффициентом сжимаемости
.
Коэффициент сжимаемости (z)учитывает различие между идеальным и реальными газами (для идеального газа z = 1).
Коэффициент сжимаемости является функцией давления, температуры и зависит от природы газа.
Для обобщения данных по коэффициентам сжимаемости различных газов был использован принцип «соответственных» состояний, сформулированный Ван-дер-Ваальсом. Принцип «соответственных» состояний утверждает, что критическое состояние действительно является одинаковым для всех веществ.
В критической точке для всех веществ r = 0, 
, 
, 
. Вещества находятся в соответственных состояниях при одинаковом удалении от критической точки.
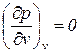
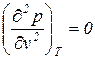
Степень удаления от критической точки определяется с помощью приведенных параметров:
приведенного давления 
; приведенной температуры 
; приведенного объема 
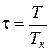
Уравнение состояния, записанное в виде F (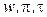 
) = 0, называется приведенным уравнением состояния. Оно не содержит индивидуальных констант вещества.
Состояния вещества, в которых они имеют одинаковые 
и 
называются соответственными. Зная параметры и по данным рис. 1.4 определяется коэффициент сжимаемости z.
12. Математическое выражение 1 го начала термодинамики (+баланс рабочего тела).
Первое начало термодинамики – это количественное выражение закона сохранения и превращения энергии.
Закон сохранения и превращения энергии является универсальным законом природы и применим ко всем явлениям. Он гласит: «запас энергии изолированной системы остается неизменным при любых происходящих в системе процессах; энергия не уничтожается и не создается, а только переходит из одного вида в другой».
Это утверждение и принимается в качестве постулата первого начала термодинамики
Первое начало термодинамики как математическое выражение закона сохранения и превращения энергии:
Внутренняя энергия изолированной системы сохраняет своё постоянное значение при всех изменениях, протекающих внутри системы, то есть 
. Изменение внутренней энергии неизолированной системы складывается из подведённой (отведённой) теплоты и подведённой (отведённой) работы, то есть 
.
в интегральной форме: 
— эффективная работа; 
— внешний теплообмен
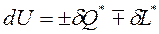
Полученные уравнения учитывают только внешние эффекты и справедливы только для обратимых процессов.
Уравнения являются математическим выражением первого начала термодинамики по внешнему балансу теплоты и работы и гласят: количество теплоты, подведенное извне, идет на изменение внутренней энергии системы и совершение работы.
В термодинамике приняты следущие знаки при определении работы и теплоты в уравнениях первого начала термодинамики: если работа выполняется телом, то она положительная; если работа подводится к телу, то она отрицательная. Если теплота сообщается телу, она имеет положительное значение; если теплота отводится от тела, она имеет отрицательное значение.
= 
+ 
Первого начала термодинамики по внешнему балансу.
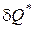
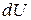
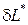
Работа необратимых потерь 
, связанная с затратами энергии на преодоление сил трения, удары и завихрения, превращается в теплоту внутреннего теплообмена ( 
)
= 
.Полное количество теплоты 
, полученное телом, равно сумме теплоты, подведенной извне 
, и теплоты внутреннего теплообмена .
; 
.
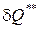
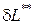
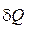
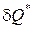
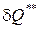
Уравнения (1.55) и (1.56) называются уравнениями первого начала термодинамики по балансу рабочего тела, и справедливы для реальных процессов.
Первое начало термодинамики по балансу рабочего тела: 
, где 
— полный или приведённый теплообмен.
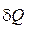
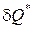
Полное количество теплоты , полученное телом, равно сумме теплоты, подведенной извне , и теплоты внутреннего теплообмена
Первое начало термодинамики по балансу рабочего тела справедливо для любых процессов протекающих в системе.
В условиях обратимого процесса, то есть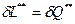 
, первое начало термодинамики по балансу рабочего тела переходит в первое начало термодинамики по внешнему балансу. Для использования этого уравнения нужно уметь его интегрировать. При интегрировании получится: 
для необратимых процессов и 
для обратимых процессов.
Видео:Уравнения состояния вещества — Игорь ЛомоносовСкачать
Закон соответственных состояний.
Если поверхности состояний разных газов геометрически подобны, то при соответствующем масштабном преобразовании они должны совпадать. Термодинамическая поверхность, которая представляет собой ряд совмещенных поверхностей состояний нескольких газов, должна описываться уравнением, не содержащим индивидуальных коэффициентов. Впервые на возможность получения такого уравнения указал Ван-дер-Ваальс. Подставив в уравнение Ван-дер-Ваальса выражения для a, b и R, включающие критические параметры, получим
.
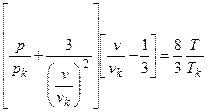
Используя приведенные параметры (р/рk=π – давление, v/vk=φ – объем, T/Tk=τ – температура), получим уравнение
известное как приведенное уравнение Ван-дер-Ваальса.
Таким образом, все вещества подчиняются одному уравнению состояния, если оно выражено через приведенные переменные. Это весьма важный закон термодинамического подобия – закон соответственных состояний. Два или несколько различных веществ с двумя равными одноименными приведенными параметрами находятся в соответственных состояниях. При этом, несмотря на присущие телам различия, их термодинамические поверхности совпадают; в результате и свойства тел (определяемые характером поверхности) в этих состояниях одинаковые. Закон соответственных состояний имеет большое прикладное значение как основа обобщения теоретических и экспериментальных данных для реальных веществ. В действительности приведенные термодинамические поверхности различных реальных веществ полностью не совпадают, и подобие является приближенным. Одним из дополнительных условий, при котором подобие выполняется более строго, является условие равенства коэффициентов сжимаемости zk в критической точке.
10. Процесс i=const. Дросселирование.
Адиабатное расширение газа в открытой системе в условиях стационарного течения без совершения внешней работы и приращения скорости на контрольной поверхности называется дросселированием. Стационарность течения предполагает в первую очередь постоянство давлений до и после дросселирования, а условие отсутствия приращения скорости течения на контрольной поверхности не исключает возможности ее местного увеличения (или уменьшения) внутри системы, например в самом дроссельном устройстве.
Для практического осуществления этого процесса на пути газа устанавливают какое-либо гидравлическое сопротивление: дроссельный вентиль, заслонку, калиброванное отверстие и пр.
Применив уравнение сохранения энергии для модели стационарной или находящейся в установившемся состоянии открытой системы для процесса дросселирования при l=0 и q=0 получим
Никаких предположений о свойствах газов не делали, поэтому полученный результат справедлив как для идеального, так и для реального газа: при дросселировании энтальпия газа не изменяется.
При дросселировании идеального газа
Для реального газа при дросселировании
Таким образом, температура реального газа при дросселировании может снижаться и повышаться.
Процесс дросселирования необратим. Для идеального газа он необратим полностью, так как не сопровождается эффектами, которые могли бы способствовать возвращению в исходное состояние. Процесс дросселирования реального газа частично обратим, так как сопровождается изменением температуры; при этом создается «тепловой резервуар» с температурой более высокой или более низкой и существует возможность использования перепада температур для получения работы (эту работу можно использовать для возвращения газа в исходное состояние).
Изменение температуры реального газа при дросселировании
.
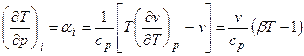
Величина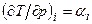 
– дифференциальный эффект Джоуля–Томсона, определяющий изменение температуры при бесконечно малом падении давления в процессе дросселирования; β – температурный коэффициент объемного расширения.
Уравнение справедливо как для газов, так и для жидкостей.
Практически при дросселировании всегда имеется конечная разность давлений, поэтому для такого процесса
.
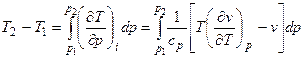
Это выражение определяет так называемый интегральный эффект Джоуля–Томсона (изменение температуры при конечной разности давлений).
11. Процесс u=const.
Если процесс расширения газа осуществить при тех же условиях, что и процесс дросселирования, т.е. без теплообмена с окружающими телами и без совершения внешней работы, но в отличие от дросселирования расширять газ в закрытой системе, т.е. не в условиях стационарного течения, а в устройстве с жесткими стенками, то полная внутренняя энергия газа в такой системе будет постоянна. Это процесс расширения u=const; какого-либо характерного названия он не имеет.
Изменение температуры газа в процессе u=const можно определить из уравнений:
.
;
.
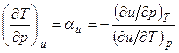
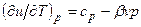
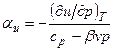
Для идеального газа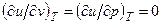 
, поэтому и dТ=0 в процессе u=const.
В процессе u=const для любого реального газа αu – всегда положительная величина, т.е. температура снижается. Интегральный эффект изменения температуры в процессе u=const
.
Дата добавления: 2015-05-16 ; просмотров: 1117 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Уравнение состояния идеального газа. 10 класс.Скачать
Закон соответственных состояний
Поскольку критические константы являются характеристическими свойствами газов, их можно использовать для создания соответствующей относительной шкалы, введя безразмерные приведенные переменные: приведенное давление рг приведенный объем Vги приведенную температуру Tr
(10.22)
Соответственными называются состояния разных веществ, имеющие одинаковые значения приведенных переменных. Согласно закону соответственных состояний, если для рассматриваемых веществ значения двух приведенных переменных одинаковы, должны совпадать и значения третьей приведенной переменной. Таким образом, уравнения состояния различных веществ, записанные в приведенных переменных, должны совпадать. Это утверждение эквивалентно постулату о существовании общего универсального приведенного уравнения состояния
(10.23)
Поскольку это приведенное уравнение не содержит в явном виде индивидуальных постоянных, оно должно быть применимо к любому веществу. Закон соответственных состояний является общим утверждением, не связанным с конкретным видом уравнения состояния. На практике закон соответственных состояний приближенно выполняется для однотипных веществ, что позволяет, например, использовать для реальных газов обобщенные диаграммы сжимаемости (рис. 10.6).
Уравнение Ван-дер-Ваальса также согласуется с законом соответственных состояний. Подставляя в исходное уравнение (10.5) постоянные а, b и R, выраженные через критические параметры уравнений (10.11)—(10.13), и переходя к приведенным переменным, получим уравнение Ван-дер- Ваальса в приведенной форме
(10.24)
Можно показать, что любое уравнение состояния, содержащее три параметра, можно представить в приведенной форме. Отсутствие универсального уравнения
говорит не о неверности закона о соответственных состояниях, а о недостаточности двух индивидуальных постоянных и R в уравнении состояния.
Рис. 10.6. Зависимость фактора сжимаемости некоторых газов от приведенного давления при разных приведенных температурах
В настоящее время понятно, почему в уравнениях состояния реальных газов двух индивидуальных параметров в общем случае не хватает, но в первом приближении этого достаточно. Причиной всех отклонений от уравнения состояния идеального газа являются межмолекулярные взаимодействия в газах. Зависимость потенциала межмолекулярного взаимодействия и от расстояния между частицами г достаточно точно описывается уравнениями, содержащими по меньшей мере четыре параметра — п, m, A и В:
(10.25)
Статистический расчет показывает, что наличие индивидуальных постоянных в уравнении межмолекулярного взаимодействия всегда приводит к появлению индивидуальных постоянных и в уравнении состояния газов. Поэтому в области значений р, V и T, для которых в реальных газах вклад межмолекулярных взаимодействий достаточно велик, в уравнениях состояния появляются индивидуальные постоянные, зависящие от параметров в уравнении межмолекулярного взаимодействия. Вместе с тем для молекул сфероидальной формы довольно хорошие результаты дает уравнение сп=12ит = 6. Поэтому часто в приближенных уравнениях состояния оказывается достаточно использовать две индивидуальные постоянные. Если же требуется описать поведение газа с более высокой точностью, необходимо использовать уравнения с большим числом постоянных. В настоящее время для возможно более точного описания свойств газов используют эмпирическое уравнение Бенедикта — Вебба Рубина (р — плотность газа):
📺 Видео
Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать
Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать
Вебинар 7. Физика. ЕГЭ 2019. Тепловое равновесие. Уравнение состояния. ИзопроцессыСкачать
Математика это не ИсламСкачать
Теорема Виета. 8 класс.Скачать
Урок 455. Уравнение ШрёдингераСкачать
Теорема Виета. Практическая часть. 2ч. 8 класс.Скачать
Теорема Виета для многочлена 3 порядка. 10 класс.Скачать
ТЕОРЕМА ВИЕТА ЗА 2 МИНУТЫСкачать
Линейная алгебра. Алексей Савватеев и Александр Тонис. Лекция 13.4. Существов. и единств. решения ДУСкачать
Обратная теорема Виета - ЛЕГКО!Скачать
✓ Свойства функций, непрерывных на отрезке. Теоремы Вейерштрасса и Коши | матан #022 | Борис ТрушинСкачать
Коробов М. В. - Физическая химия. Часть 1 - Основные понятия, свойства системыСкачать
Коробов М. В. - Физическая химия. Часть 1 - Теплота и работа. Первый закон термодинамикиСкачать
Теорема Виета. Практическая часть. 1ч. 8 класс.Скачать
Теорема Виета. Вебинар | МатематикаСкачать
Теорема Виета ПРЯМАЯ и ОБРАТНАЯ, в чем разница? - ЗА 4 МИНУТЫСкачать
Лекция №3 "Необратимые процессы. Термодинамические потенциалы" (Попов П.В.)Скачать
