Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Определение 1: Два уравнения с одной переменной f ( x )= g ( x ) и p ( x )= h ( x )
называются равносильными , если множества их корней совпадают.
Определение 2: Если каждый корень уравнения f ( x )= g ( x ) (1)
является в тоже время корнем уравнения p ( x )= h ( x ) (2),
то уравнение (2) называют следствием уравнения (1).
Очевидно: Два уравнения равносильны тогда и только тогда, когда каждое из них является следствием другого.
Схема решения любого уравнения:
1.Технический этап. Осуществляется преобразование уравнения (1)→(2)→(3)→(4) …
2 . Анализ решения. Все ли преобразования были равносильными?
Реализация данного плана связана с поиском ответов на четыре вопроса:
Как узнать, является ли переход от одного уравнения к другому равносильным преобразованием?
Какие преобразования могут перевести данное уравнение в уравнение-следствие?
Если мы в конечном итоге решили уравнение-следствие, то как сделать проверку в случае, когда она сопряжена со значительными вычислительными трудностями?
В каких случаях при переходе от одного уравнения к другому может произойти потеря корней и как этого не допустить?
1.Теоремы о равносильности уравнений.
Теорема 1. Если какой либо член уравнения перенести из одной части уравнения в другую с противоположным знаком, то получится уравнение, равносильное данному.
Теорема 2. Если обе части уравнения возвести в одну и ту же нечетную степень, то получится уравнение, равносильное данному.
Теорема 3. Показательное уравнение а f ( x ) =а g ( x ) ( где а>0, а≠1) равносильно уравнению f ( x )= g ( x ).
Определение: Областью определения уравнения f ( x )= g ( x ) или областью допустимых значений (ОДЗ) переменной называют множество тех значений переменной х, при которых одновременно имеют смысл выражения f ( x ) и g ( x ).
Теорема 4. Если обе части уравнения f ( x )= g ( x ) умножить на одно и то же выражение h ( x ), которое:
А) имеет смысл всюду в области определения (в ОДЗ) уравнения f ( x )= g ( x )
Б) нигде в этой области не обращается в 0 –
то получится уравнение f ( x ) h ( x )= g ( x ) h ( x ), равносильное данному.
Следствие («спокойное» утверждение): Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
Теорема 5. Если обе части уравнения f ( x )= g ( x ) неотрицательны в области определения уравнения, то после возведения обеих его частей в одну и ту же четную степень n получится уравнение, равносильное данному f ( x ) n = g ( x ) n .
Теорема 6. Если f ( x ) >0 и g ( x ) >0, то логарифмическое уравнение log а f ( x )= log а g ( x ), где а>0, а≠1, равносильно уравнению f ( x )= g ( x ).
2. Преобразование данного уравнения в уравнение-следствие.
Если в процессе решения уравнения мы применили заключение одной из теорем 4,5,6, не проверив выполнения ограничительных условий, заложенных в формулировках теорем, то получится уравнение-следствие.
Некоторые переходы от одного уравнения к другому приводят к расширению области определения уравнения. Именно в добавленную часть ОДЗ и «проникают» посторонние корни.
Причины расширения области определения уравнения.
Освобождение в процессе решения уравнения от знаменателей, содержащих переменную величину.
Освобождение в процессе решения уравнения от знаков корней четной степени.
Освобождение в процессе решения уравнения от знаков логарифмов.
Обязательна проверка всех найденных корней, если:
произошло расширение области определ6ения уравнения.
осуществлялось возведение обеих частей уравнения в одну и ту же четную степень.
выполнялось умножение обеих частей уравнения на одно и то же выражение с переменной (разумеется, имеющее смысл во всей области определения уравнения).
3. О проверке корней.
Как правило, самый легкий обходной путь проверки – по области определения (ОДЗ) заданного уравнения. Но не переоценивайте этот способ: он является полноценным только в том случае, когда при решении уравнения других причин нарушения равносильности, кроме расширения области определения, не было (это чаще всего бывает в логарифмических уравнениях). При решении же иррациональных уравнений, где используется метод возведения в квадрат, способ проверки найденных корней по ОДЗ не выручит; лучше, если это возможно, делать проверку подстановкой.
О потере корней.
Причины потери корней при решении уравнений:
деление обеих частей уравнения на одно и то же выражение h ( x ) (кроме тех случаев, когда точно известно, что всюду в области определения уравнения выполняется условие h ( x ) ≠0).
сужение ОДЗ в процессе решения уравнения.
замена уравнения h ( f ( x ))= h ( g ( x )) уравнением f ( x )= g ( x ) в том случае, если функция
у= h ( x ) – немонотонная функция.
Этот метод можно применить только в том случае, если функция у= h ( x ) – монотонная функция.
Видео:Логарифмы с нуля за 20 МИНУТ! Introduction to logarithms.Скачать
Теорема о равносильности логарифмических уравнений
Полный перечень схем равносильных преобразований, которые облегчают решение логарифмических неравенств.
Пусть $$ fleft( x right) = f $$, $$ gleft( x right) = g $$ — функции, $$ a,;b,;c $$ — действительные числа.
1. $$ log _a f vee 0 Leftrightarrow left( right)left( right) vee 0$$, ОДЗ: $$ left< begin f > 0; \ a > 0,<rm>a ne 1. \ end right.$$
2. $$ log _a f vee b Leftrightarrow left( right)left( right) vee 0 $$, ОДЗ: $$ left< begin f > 0; \ a > 0,<rm>a ne 1. \ end right.$$
3. $$ log _a f vee log _a g Leftrightarrow left( right)left( right) vee 0 $$, ОДЗ: $$ left< begin f > 0,<rm>g > 0; \ a > 0,<rm>a ne 1. \ end right. $$
4. $$ log _a f vee log _c f Leftrightarrow left( right)left( right)left( right)left( right) vee $$, ОДЗ: $$ left< begin f > 0; \ a > 0,<rm>a ne 1; \ c > 0,<rm>c ne 1. \ end right. $$
5. $$ left( right) vee 0 Leftrightarrow left( right)left( right) vee 0] $$, ОДЗ: $$ left< begin f > 0,<rm>g > 0; \ a > 0,<rm>a ne 1. \ end right. $$
6. $$ log _a f cdot log _c g vee 0 Leftrightarrow left( right)left( right)left( right)left( right) vee 0 $$, ОДЗ: $$ left< begin f > 0,<rm>g > 0; \ a > 0,<rm>a ne 1; \ c > 0,<rm>c ne 1. \ end right. $$
Замечание. Если в этих схемах $$ a,;b,;c$$ (действительные числа) заменить элементарными функциями, то получаться схемы равносильных преобразований логарифмических неравенств, содержащих в основании неизвестную величину.
Видео:11 класс, 17 урок, Логарифмические уравненияСкачать
Теорема о равносильности логарифмических уравнений
Логарифмическим уравнениям и неравенствам в вариантах ЕГЭ по математике посвящена задача C3. Научиться решать задания C3 из ЕГЭ по математике должен каждый ученик, если он хочет сдать предстоящий экзамен на «хорошо» или «отлично». В данной статье представлен краткий обзор часто встречающихся логарифмических уравнений и неравенств, а также основных методов их решения.
Итак, разберем сегодня несколько примеров логарифмических уравнений и неравенств, которые предлагались учащимся в вариантах ЕГЭ по математике прошлых лет. Но начнет с краткого изложение основных теоретических моментов, которые нам понадобятся для их решения.
Видео:Логарифмические уравнения. 11 класс.Скачать
Логарифмическая функция
Определение
0,, ane 1 ]» title=»Rendered by QuickLaTeX.com»/>
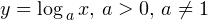
называют логарифмической функцией.
Основные свойства
Основные свойства логарифмической функции y = loga x:
| | a > 1 | 0 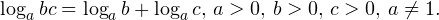 0,, b>0,, c>0,, ane 1. ]» title=»Rendered by QuickLaTeX.com»/>• Логарифм частного двух положительных чисел равен разности логарифмов этих чисел:
• Если a и b — положительные числа, причем a ≠ 1, то для любого числа r справедливо равенство:
• Если a, b, c — положительные числа, причем a и c отличны от единицы, то имеет место равенство (формула перехода к новому основанию логарифма):
Видео:Решение логарифмических уравнений #shortsСкачать  Решение логарифмических уравнений и неравенствПример 1. Решите уравнение:
Решение. В область допустимых значений входят только те x, при которых выражение, находящееся под знаком логарифма, больше нуля. Эти значения определяются следующей системой неравенств:
С учетом того, что получаем промежуток, определяющий область допустимых значений данного логарифмического уравнения:
На основании теоремы 1, все условия которой здесь выполнены, переходим к следующему равносильному квадратичному уравнению:
В область допустимых значений входит только первый корень. Ответ: x = 7. Пример 2. Решите уравнение:
Решение. Область допустимых значений уравнения определяется системой неравенств:
Очевидно, что эти два условия противоречат друг другу. То есть нет ни одного такого значения x, при котором одновременно выполнялись бы оба неравенства. Область допустимых значений уравнения является пустым множеством, а значит решений у данного логарифмического уравнения нет. Ответ: корней нет. Обратите внимание, что в этом задании нам вообще не пришлось искать корни уравнения. Достаточно оказалось определить, что его область допустимых значений не содержит ни одного действительно числа. Это одно из преимуществ такой последовательности решения логарифмических уравнений и неравенств (начинать с определения области допустимых значений уравнения, а затем решать его путем равносильных преобразований). Примет 3. Решите уравнение:
Решение. Область допустимых значений уравнения определяется здесь легко: x > 0.
Уравнение принимает вид:
Оба ответа входят в область допустимых значений уравнения, поскольку являются положительными числами. Пример 4. Решите уравнение:
Решение. Вновь начнем решение с определения области допустимых значений уравнения. Она определяется следующей системой неравенств:
Воспользовавшись правилом сложения логарифмов, переходим к равносильному в области допустимых значений уравнению:
Основания логарифмов одинаковы, поэтому в области допустимых значений можно перейти к следующему квадратному уравнению:
Первый корень не входит в область допустимых значений уравнения, второй — входит. Ответ: x = -1. Пример 5. Решите уравнение:
Решение. Будем искать решения в промежутке x > 0, x≠1. Преобразуем уравнение к равносильному:
Оба ответа входят в область допустимых значений уравнения. Пример 6. Решите уравнение:
Решение. Система неравенств, определяющая область допустимых значений уравнения, имеет на этот раз вид: Используя свойства логарифма, преобразуем уравнение к равносильному в области допустимых значений уравнению:
Используя формулу перехода к новому основанию логарифма, получаем:
В область допустимых значений входит только один ответ: x = 4. Перейдем теперь к логарифмическим неравенствам. Это как раз то, с чем вам придется иметь дело на ЕГЭ по математике. Для решения дальнейших примеров нам потребуется следующая теорема: Теорема 2. Если f(x) > 0 и g(x) > 0, то: Решение. Начнем с определения области допустимых значений неравенства. Выражение, стоящее под знаком логарифмической функции, должно принимать только положительные значения. Это значит, что искомая область допустимых значений определяется следующей системой неравенств:
Так как в основании логарифма стоит число, меньшее единицы, соответствующая логарифмическая функция будет убывающей, а потому равносильным по теореме 2 будет переход к следующему квадратичному неравенству:
Окончательно, с учетом области допустимых значений получаем ответ:
Пример 8. Решите неравенство:
Решение. Вновь начнем с определения области допустимых значений:
На множестве допустимых значений неравенства проводим равносильные преобразования:
После сокращения и перехода к равносильному по теореме 2 неравенству получаем:
С учетом области допустимых значений получаем окончательный ответ:
Пример 9. Решите логарифмическое неравенство:
Решение. Область допустимых значений неравенства определяется следующей системой:
Видно, что в области допустимых значений выражение, стоящее в основании логарифма, всегда больше единицы, а потому равносильным по теореме 2 будет переход к следующему неравенству:
С учетом области допустимых значений получаем окончательный ответ:
Пример 10. Решите неравенство:
Решение. Область допустимых значений неравенства определяется системой неравенств:
I способ. Воспользуемся формулой перехода к новому основанию логарифма и перейдем к равносильному в области допустимых значений неравенству:
Неравенство будет равносильно двум системам. Первой:
Итак, окончательный ответ:
II способ. Решаем методом интервалов. Преобразуем неравенство к виду:
Вычтем из знаменателя
С учетом того, что выражения
Множество решений данного неравенства Итак, Итак, что нужно для того, чтобы решать логарифмические уравнения и неравенства?
Главное же требование — это настойчивость в достижении своей цели. Учитесь, тренируйтесь, если нужно — ежедневно, изучайте и запоминайте на примерах основные способы решения неравенств и их систем, анализируйте возникающие ошибки и не допускайте их в будущем. За помощью в этом нелегком деле вы можете обратиться к своему школьному учителю по математике, репетитору, родителям, друзьям и знакомым, книгам, а также огромному количеству материалов, доступных на просторах Интернета. Желаю вам успехов в подготовке к Единому государственному экзамену по математике. 💡 Видео§19 Логарифмические уравненияСкачать  11 класс, 26 урок, Равносильность уравненийСкачать  Проще простого! Как решить Логарифмическое Уравнение?Скачать  Круговорот воды в природе ➜ Решение логарифмических уравнений из ЕГЭ #ShortsСкачать  84 людей этого не знают! Секретный способ решения Логарифмических УравненийСкачать  Интересная задача на логарифмы в ЕГЭСкачать  Решение логарифмических уравнений. Вебинар | МатематикаСкачать  Алгебра 10 класс (Урок№27 - Логарифмические уравнения.)Скачать  Учимся решать сложные логарифмические уравненияСкачать  Умножаем логарифмы В УМЕ🧠Скачать  Логарифмические уравнения. Видеоурок 18. Алгебра 10 классСкачать  Логарифмические уравнения 🥷🏿Скачать  ✓ Как решать логарифмические уравнения и неравенства, не помня свойства логарифмов | Борис ТрушинСкачать  Равносильность уравнений и неравенств. Видеоурок 7. Алгебра 10 классСкачать  Алгебра 10 класс (Урок№19 - Равносильные уравнения и неравенства.)Скачать  |
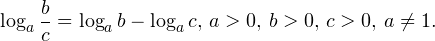0,, b>0,, c>0,, ane 1. ]» title=»Rendered by QuickLaTeX.com»/>
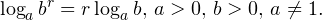0,, b>0,, ane 1. ]» title=»Rendered by QuickLaTeX.com»/>
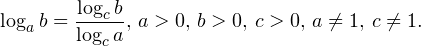0,, b>0,, c>0,, ane 1,, cne 1. ]» title=»Rendered by QuickLaTeX.com»/>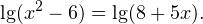
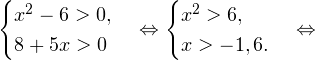0, \ 8+5x > 0 end Leftrightarrow begin x^2 > 6, \ x>-1,6. end Leftrightarrow ]» title=»Rendered by QuickLaTeX.com»/>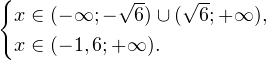
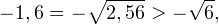-sqrt, ]» title=»Rendered by QuickLaTeX.com»/>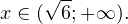
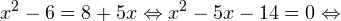
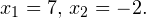
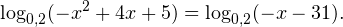
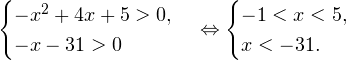0, \ -x-31>0 endLeftrightarrow begin -1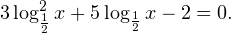
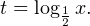
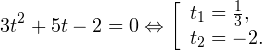
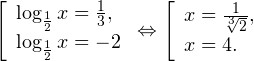
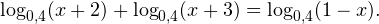
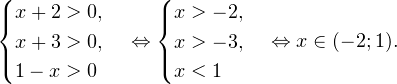0, \ x+3>0, \ 1-x>0 endLeftrightarrow begin x>-2, \ x>-3, \ x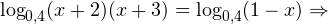
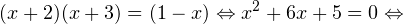
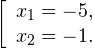
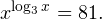
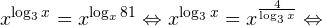
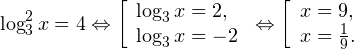
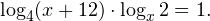
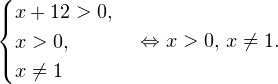0, \ x>0, \ xne 1 endLeftrightarrow x>0,, xne 1. ]» title=»Rendered by QuickLaTeX.com»/>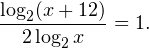
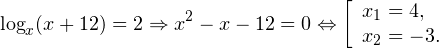
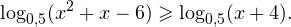
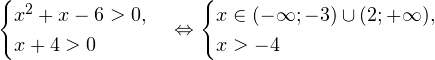0, \ x+4>0 endLeftrightarrow begin xin(-mathcal;-3)cup(2;+mathcal), \ x>-4 end ]» title=»Rendered by QuickLaTeX.com»/>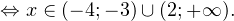
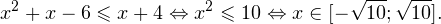
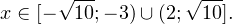
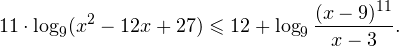
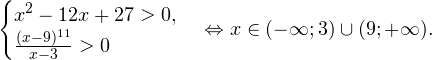0, \ frac<(x-9)^>>0 endLeftrightarrow xin(-mathcal;3)cup(9;+mathcal). ]» title=»Rendered by QuickLaTeX.com»/>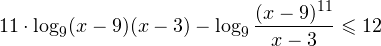
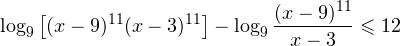
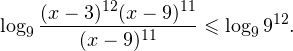
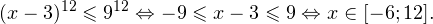
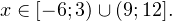
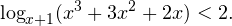
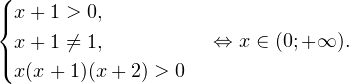0, \ x+1ne 1,\ x(x+1)(x+2)>0 endLeftrightarrow xin (0;+mathcal). ]» title=»Rendered by QuickLaTeX.com»/>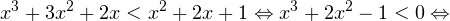
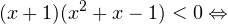
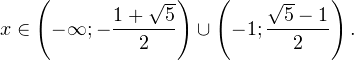
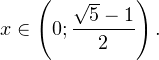
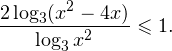
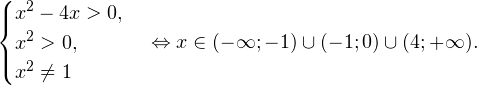0, \ x^2>0, \ x^2ne 1 endLeftrightarrow xin(-mathcal;-1)cup(-1;0)cup(4;+mathcal). ]» title=»Rendered by QuickLaTeX.com»/>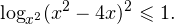
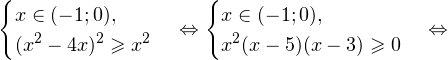
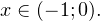
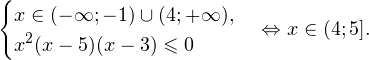
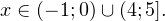
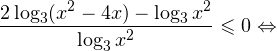
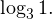Это ничего не изменит, поскольку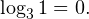 
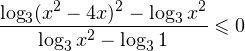
и 
— одного знака при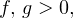 
0,» title=»Rendered by QuickLaTeX.com» height=»18″ width=»74″ style=»vertical-align: -4px;»/> в области допустимых значений имеет место следующий равносильный переход: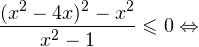
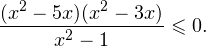
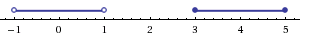
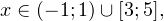а с учетом области допустимых значений получаем тот же результат: 