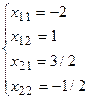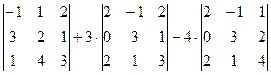Алгебра и теория чисел
Лекция 3
Системы линейных уравнений
План
1. Основные понятия и обозначения.
2. Элементарные преобразования системы линейных уравнений.
3. Ступенчатая матрица. Приведение матрицы к ступенчатому виду.
Литература
1. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. 1997, с. 25-48.
2. Ермаков В.И. Общий курс высшей математики. М.: Инфра — М, 2000. с. 5-22
3. Кремер Н.Ш. Высшая математика для экономистов. М.: Юнити, 2000. с. 38-56.
1. Основные понятия и обозначения. Простейшие системы двух линейных уравнений с двумя неизвестными изучаются в средней школе:

Известно, что справедлив один из следующих трех случаев: либо система имет одно решение, либо имеет бесконечно много решений, либо не имеет решений. В этом параграфе мы будем рассматривать общие системы линейных уравнений и установим это утверждение в общем случае кроме того изложим один из наиболее удобных методов решения систем линейных уравнений — метод последовательного исключения неизвестных или метод Гаусса по имени выдающегося немецкого математика К. Ф. Гаусса (1777-1855).
Определение 1.Системой m линейных уравнений с n неизвестными

где a11 ,a12 . amn — фиксированные числа (действительные, комплексные или принадлежащие некоторому полю) , называемые коэффициентами при неизвестных, b1 ,b2 . bm — фиксированные числа, называемые свободными членами.
Если все свободные члены в системе линейных уравнений равны нулю, то система линейных уравнений называется однородной.
Определение 2.Решением системы линейных уравнений (1) называется такой упорядоченный набор n чисел 
Система называется совместной, если она имеет хотя бы одно решение, и называется несовместной, если она не имеет решений. Совместная система называется определенной, если она имеет одно решение, и называется неопределенной, если она не имеет решений.
Пусть S1 , S2 системы линейных уравнений с одним и тем же числом неизвестных, X1 , X2 — множества их решений соответственно.
Определение 3.Говорят, что система линейных уравнений S2 следствие системы S1 и S2 , если каждое решение системы S1 является решением системы S2 ,т.е. 

Определение 4. Говорят, что системы S1 и S2 равносильны, если каждое решение системы S1 является решением системы S2 и каждое решение системы S2 является решением системы S1 , т.е. 

Отношение следования и равносильности обладают следующими свойствами.
1. Если 


Действительно, если 

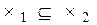



2. 
3. Если 

4. Если 
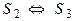
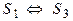
Свойства 2, 3, 4 доказываются аналогично.
Элементарные преобразования системы линейных уравнений.
Определение 5. Элементарными преобразованиями системы линейных уравнений называются ее следующие преобразования:
1) перестановка любых двух уравнений местами;
2) умножение обеих частей одного уравнения на любое число 
3) прибавление к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на любое число k ;
(при этом все остальные уравнения остаются неизменными).
Нулевым уравнением называем уравнение следующего вида:

Теорема 1. Любая конечная последовательность элементарных преобразований и преобразование вычеркивание нулевого уравнения переводит одну систему линейных уравнений в равносильную ей другую систему линейных уравнений.
Доказательство.В силу свойства 4 предыдущего пункта достаточно доказать теорему для каждого преобразования отдельно.
1. При перестановке уравнений в системе местами сами уравнения неизменяются, поэтому по определению полученная система равносильная первоначальной .
2. В силу первой части доказательства достаточно доказать утверждение для первого уравнения. Умножим первое уравнение системы (1) на число 

Пусть 






Умножая его на число k,получим верное числовое равенство:

т.о. устанавливаем, что 
Обратно, если 





Отсюда по определению 4 система (1) равносильна системе (2).
3. В силу первой части доказательства достаточно доказать утверждение для первого и второго уравнения системы . Прибавим к обеим частям первому уравнению системы соответствующие части второго умноженные на число k , получим систему

Пусть 




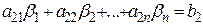
Прибавляя почленно к первому равенству второе, умноженное на число k получим верное числовое равенство:

Обратно, если 



Отсюда по определению 4 система (1) равносильна системе (5).
4. Так как нулевому уравнению удовлетворяет любой упорядоченный набор из n чисел, то при вычеркивании нулевого уравнения в системе получим систему равносильную исходной.
Ступенчатая матрица.
Определение 6.Матрицей размерности 
содержащая mn чисел, расположенных в m строк и n столбцов, числа 

Определение 7. Матрицей ступенчатого вида называется такая матрица, которая обладает свойствами:
1) в каждой строке матрицы имеется неравный нулю элемент;
2) в каждой строке матрицы, начиная со второй, первый слева неравный нулю элемент расположен правее первого слева неравного нулю элемента предыдущей строки матрицы.
Матрицу ступенчатого вида называют также трапециидальной матрицей, а квадратную матрицу ступенчатого вида называют треугольной матрицей. Ниже показаны две не ступенчатые матрицы и три ступенчатые матрицы (последняя матрица треугольная).







Определение 8. Элементарными преобразованиями строк матрицы называются следующие ее преобразования:
1) перестановка любых двух строк матрицы местами;
2) умножение одной строки матрицы на любое число 
3) прибавление к одной строке матрицы другой ее строки умноженной на любое число k ;
(при этом все остальные строки матрицы остаются неизменными).
Аналогично можно рассматривать элементарные преобразования столбцов матрицы.
Теорема 2. Любую ненулевую матрицу конечным числом элементарных преобразований и преобразований вычеркивания нулевой строки можно привести к матрице ступенчатого вида.
Доказательство.Доказательство проводим методом математической индукции по числу m строк матрицы. Для m=1 утверждение теоремы справедливо, так как ненулевая однострочная матрица по определению имеет ступенчатый вид.
Предположим, что утверждение теоремы доказано для матриц, имеющих m-1 строку и докажем его для матриц, в которых содержится m строк. Пусть первый слева отличный от нуля столбец данной матрицы имеет номер k , так как матрица ненулевая, то такой столбец найдется, и матрица имеет вид:
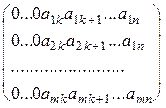
Можем считать, что элемент 




Рассмотрим матрицу, состоящую из последних m-1 строк матрицы (9):

Если матрица (10) нулевая, то все строки в матрице (9) кроме первой нулевые. Вычеркивая их, приходим к матрице ступенчатого вида. Если матрица (10) ненулевая, то по индуктивному предположению конечным число элементарных преобразований и преобразований вычеркивания нулевой строки может быть приведена к матрице ступенчатого вида: 
где элементы 



элементы 


4. Метод Гаусса. Системе линейных уравнений (1) соответствуют три матриц



Первая матрица называется матрицей системы, вторая — расширенной или присойдиненной матрицей системы, третья — столбцом свободных членов.
Система линейных уравнений называется системой ступенчатого вида, если расширенная матрица системы есть матрица ступенчатого вида. Неизвестные с коэффициентами неравными нулю, которые стоят первыми в уравнениях системы ступенчатого вида называются главными неизвестными, а остальные неизвестные называются свободными.
Линейное уравнение, в котором все коэффициенты равны нулю, а свободный член не равен нулю, т.е. уравнение вида:

не имеет решений. Действительно, если 

Пусть не все уравнения системы (1) нулевые. Тогда и расширенная матрица системы (1) ненулевая. По теореме 2 ее можно конечным числом элементарных преобразований и преобразований выбрасывания нулевой строки можно привести к матрице ступенчатого вида. Полученной матрице соответствует система линейных уравнений ступенчатого вида. Этим преобразованиям расширенной матрицы системы (1) соответствуют такие же преобразования системы линейных уравнений (1). По теореме 1 они переводят систему (1) в равносильную систему линейных уравнений, которая будет являются системой ступенчатого вида.
Таким образом мы доказали первую часть следующей теоремы.
Теорема 3.Любую систему линейных уравнений , содержащую ненулевое уравнение конечным числом элементарных преобразований и преобразований вычеркивания нулевого уравнения можно привести к равносильной ей системе ступенчатого вида. При этом возможны следующие три случая.
1. Если в полученной системе линейных уравнений ступенчатого вида есть противоречивое уравнение, то данная система не имеет решений.
2. Если в полученной системе линейных уравнений ступенчатого вида нет противоречивого уравнения и число уравнений в полученной системе равно числу неизвестных, то данная система имеет единственное решение.
3. Если в полученной системе линейных уравнений ступенчатого вида нет противоречивого уравнения и число уравнений в полученной системе меньше числа неизвестных, то данная система имеет бесконечно много решение.
Доказательство.Пусть дана система (1), содержащая ненулевое уравнение. По выше доказанному, она конечным числом элементарных преобразований она может быть преобразована к равносильной ей системе уравнений ступенчатого вида. Возможны случаи.
В полученной системе ступенчатого вида есть противоречивое уравнение. Тогда ни один набор чисел 
В полученной системе ступенчатого вида нет противоречивого уравнения. Тогда в каждом из уравнений системы ступенчатого вида содержится главное неизвестное. Отсюда получаем, что число главных неизвестных, а тем более число всех неизвестных, не менее числа уравнений в системе ступенчатого вида. Тогда возможны под случаи:
В системе ступенчатого вида число уравнений равно числу неизвестных, т. е. система имеет вид:

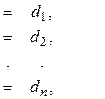
где 


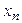




В системе ступенчатого вида число уравнений меньше числа неизвестных. В этом случае матрица полученной системы имеет вид (11), а
систему можно записать в виде:




где 




Следствие.Если в системе однородных уравнений число неизвестных больше числа уравнений, то система имеет бесконечно много решений.
Действительно, система однородных уравнений всегда имеет нулевое решение 
Метод исследования и решения систем линейных уравнений, изложенный в доказательстве теорем 3 называется методом Гаусса.
Пример 1.Решить систему
Составим расширенную матрицу системы и приведем ее к ступенчатому виду:

Составим по полученной матрице ступенчатого вида систему линейных уравнений ступенчатого вида:
В полученной системе число уравнений равно числу неизвестных и полученная система имеет единственное решение, которое двигаясь вверх последовательно находим:
Решение системы 
Пример 2.Решить систему
Составим расширенную матрицу системы и приведем ее к ступенчатому виду:

Видео:Как привести матрицу к ступенчатому виду - bezbotvyСкачать

Теорема 1. Всякую матрицу путем элементарных преобразований строк можно привести к ступенчатому виду
Институт сервиса, туризма и дизайна (филиал) в г. Пятигорске
Лекции по дисциплине «Алгебра»
Составитель: Чебоксаров А.Б.
Содержание
| Раздел 1. Линейная алгебра. |
| Лекция 1. Матрицы. |
| Лекция 2. Определители. |
| Лекция 3. Системы линейных уравнений. Метод Гаусса решения систем. |
| Лекция 4. Другие методы решения систем линейных уравнений: матричный метод и метод Крамера. |
| Лекция 5. Условие совместности системы линейных уравнений. Общее решение однородной линейной системы. |
| Лекция 6,7. Линейные преобразования. Квадратичные формы. |
| Раздел 3. Комплексные числа. |
| Лекция 8. Понятие комплексных чисел. Действие с комплексными числами.. |
| Лекция 9. Показательная форма комплексного числа. Разложение многочлена на множители. |
| Примерный перечень вопросов к экзамену |
Раздел 1. Линейная алгебра.
Лекция 1. Матрицы.
Определение. Матрицейразмера m´n, где m- число строк, n- число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются aij, где i- номер строки, а j- номер столбца.
А =
Основные действия над матрицами.
Матрица может состоять как из одной строки, так и из одного столбца. Вообще говоря, матрица может состоять даже из одного элемента.
Определение. Если число столбцов матрицы равно числу строк (m=n), то матрица называется квадратной.
Определение. Матрица вида:
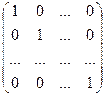
называется единичной матрицей.
Определение. Если amn = anm , то матрица называется симметрической.
Пример. 
Определение.Квадратная матрица вида 
Сложение и вычитание матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций является то, что они определены только для матриц одинакового размера. Таким образом, возможно определить операции сложения и вычитания матриц:
Определение. Суммой (разностью) матриц является матрица, элементами которой являются соответственно сумма (разность) элементов исходных матриц.
Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число.
Пример. Даны матрицы А = 

2А = 

Операция умножения матриц.
Определение: Произведением матриц называется матрица, элементы которой могут быть вычислены по следующим формулам:


Из приведенного определения видно, что операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй.
Свойства операции умножения матриц.
1)Умножение матриц не коммутативно, т.е. АВ ¹ ВА даже если определены оба произведения. Однако, если для каких – либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными.
Самым характерным примером может служить единичная матрица, которая является перестановочной с любой другой матрицей того же размера.
Перестановочными могут быть только квадратные матрицы одного и того же порядка.
А×Е = Е×А = А
Очевидно, что для любых матриц выполняются следующее свойство:
где О – нулеваяматрица.
2) Операция перемножения матриц ассоциативна, т.е. если определены произведения АВ и (АВ)С, то определены ВС и А(ВС), и выполняется равенство:
3) Операция умножения матриц дистрибутивна по отношению к сложению, т.е. если имеют смысл выражения А(В+С) и (А+В)С, то соответственно:
А(В + С) = АВ + АС
4) Если произведение АВ определено, то для любого числа a верно соотношение:
5) Если определено произведение АВ , то определено произведение В Т А Т и выполняется равенство:
(АВ) Т = В Т А Т , где
индексом Т обозначается транспонированная матрица.
6) Заметим также, что для любых квадратных матриц det (AB) = detA×detB.
Понятие det (определитель, детерминант) будет рассмотрено ниже.
Определение. Матрицу В называют транспонированнойматрицей А, а переход от А к В транспонированием, если элементы каждой строки матрицы А записать в том же порядке в столбцы матрицы В.
А = 

В качестве следствия из предыдущего свойства (5) можно записать, что:
(ABC) T = C T B T A T ,
при условии, что определено произведение матриц АВС.
Пример. Даны матрицы А = 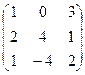


A T = 




aC = 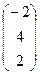

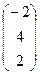

Пример. Найти произведение матриц А = 
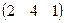
АВ = 
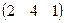

ВА = 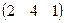

Пример. Найти произведение матриц А= 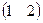
АВ = 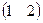



Лекция 2. Определители.
Определение. Определителемквадратной матрицы А= 
det A = 
М1к – детерминант матрицы, полученной из исходной вычеркиванием первой строки и k – го столбца. Следует обратить внимание на то, что определители имеют только квадратные матрицы, т.е. матрицы, у которых число строк равно числу столбцов.
Предыдущая формула позволяет вычислить определитель матрицы по первой строке, также справедлива формула вычисления определителя по первому столбцу:
det A =
Вообще говоря, определитель может вычисляться по любой строке или столбцу матрицы, т.е. справедлива формула:
detA = 
Очевидно, что различные матрицы могут иметь одинаковые определители.
Определитель единичной матрицы равен 1.
Для указанной матрицы А число М1к называется дополнительным минором элемента матрицы a1k. Таким образом, можно заключить, что каждый элемент матрицы имеет свой дополнительный минор. Дополнительные миноры существуют только в квадратных матрицах.
Определение. Дополнительный минор произвольного элемента квадратной матрицы aij равен определителю матрицы, полученной из исходной вычеркиванием i-ой строки и j-го столбца.
Свойство1. Важным свойством определителей является следующее соотношение:
Свойство 2. det (AB) = detA×detB
Свойство 3.Если в квадратной матрице поменять местами какие-либо две строки (или столбца), то определитель матрицы изменит знак, не изменившись по абсолютной величине.
Свойство 4. При умножении столбца (или строки) матрицы на число ее определитель умножается на это число.
Определение: Столбцы (строки) матрицы называются линейно зависимыми, если существует их линейная комбинация, равная нулю, имеющая нетривиальные (не равные нулю) решения.
Свойство 6. Если в матрице А строки или столбцы линейно зависимы, то ее определитель равен нулю.
Свойство 7. Если матрица содержит нулевой столбец или нулевую строку, то ее определитель равен нулю. (Данное утверждение очевидно, т.к. считать определитель можно именно по нулевой строке или столбцу.)
Свойство 8. Определитель матрицы не изменится, если к элементам одной из его строк(столбца) прибавить(вычесть) элементы другой строки(столбца), умноженные на какое-либо число, не равное нулю.
Свойство 9. Если для элементов какой- либо строки или столбца матрицы верно соотношение: d = d1 ± d2 , e = e1 ± e2 , f = f1 ± f2 , то верно:
Пример. Вычислить определитель матрицы А =
Пример:. Даны матрицы А = 
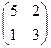
1-й способ: det A = 4 – 6 = -2; det B = 15 – 2 = 13; det (AB) = det A ×det B = -26.
2- й способ: AB = 
Элементарные преобразования матрицы.
Определение. Элементарными преобразованиями матрицы назовем следующие преобразования:
1) умножение строки на число, отличное от нуля;
2) прибавление к элемнтам одной строки элементов другой строки;
3) перестановка строк;
4) вычеркивание (удаление) одной из одинаковых строк (столбцов);
Те же операции, применяемые для столбцов, также называются элементарными преобразованиями.
С помощью элементарных преобразований можно к какой-либо строке или столбцу прибавить линейную комбинацию остальных строк ( столбцов ).
Выше было использовано понятие дополнительного минора матрицы. Дадим определение минора матрицы.
Определение. Если в матрице А выделить несколько произвольных строк и столько же произвольных столбцов, то определитель, составленный из элементов, расположенных на пересечении этих строк и столбцов называется миноромматрицы А. Если выделено s строк и столбцов, то полученный минор называется минором порядка s.
Заметим, что вышесказанное применимо не только к квадратным матрицам, но и к прямоугольным.
Если вычеркнуть из исходной квадратной матрицы А выделенные строки и столбцы, то определитель полученной матрицы будет являться дополнительным минором.
Определение. Алгебраическим дополнением минора матрицы называется его дополнительный минор, умноженный на (-1) в степени, равной сумме номеров строк и номеров столбцов минора матрицы.
В частном случае, алгебраическим дополнением элемента матрицы называется его дополнительный минор, взятый со своим знаком, если сумма номеров столбца и строки, на которых стоит элемент, есть число четное и с противоположным знаком, если нечетное.
Теорема Лапласа. Если выбрано s строк матрицы с номерами i1, … ,is, то определитель этой матрицы равен сумме произведений всех миноров, расположенных в выбранных строках на их алгебраические дополнения.
Определим операцию деления матриц как операцию, обратную умножению.
Определение.Если существуют квадратные матрицы Х и А одного порядка, удовлетворяющие условию:
где Е — единичная матрица того же самого порядка, что и матрица А, то матрица Х называется обратнойк матрице А и обозначается А -1 .
Каждая квадратная матрица с определителем, не равным нулю имеет обратную матрицу и притом только одну.
Рассмотрим общий подход к нахождению обратной матрицы.
Исходя из определения произведения матриц, можно записать:
AX = E Þ 
Таким образом, получаем систему уравнений:

Решив эту систему, находим элементы матрицы Х.
Пример. Дана матрица А = 
Таким образом, А -1 = 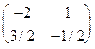
Однако, такой способ не удобен при нахождении обратных матриц больших порядков, поэтому обычно применяют следующую формулу:

где Мji— дополнительный минор элемента аji матрицы А.
Пример. Дана матрица А = 
Таким образом, А -1 = 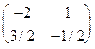
Cвойства обратных матриц.
Укажем следующие свойства обратных матриц:
2) (AB) -1 = B -1 A -1
3) (A T ) -1 = (A -1 ) T .
Пример. Дана матрица А = 
А 2 = АА = 

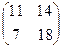

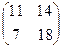

Отметим, что матрицы 
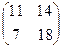
Пример. Вычислить определитель 




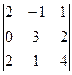

Значение определителя: -10 + 6 – 40 = -44.
Лекция 3. Системы линейных уравнений. Метод Гаусса решения систем.
Линейным уравнением с неизвестными х1,x2,…,xn над полем К называется уравнение вида
где коэффициенты a1,a2,…,an и свободный член b суть элементы поля К. Линейное уравнение называется однородным, если b = 0.
Система линейных уравнений с n неизвестными в общем виде записывается следующим образом:

называется матрицей коэффициентов, а матрица
A * =
— расширенной матрицей системы (9.1).
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной — в противном случае. Совместная система может иметь одно или более решений. Решить систему уравнений — это значит найти все ее решения. Подчеркнем, что одно решение системы уравнений с n неизвестными — это упорядоченный набор из n чисел, т.е. элемент пространства К n .
Существует простой общий метод решения систем линейных уравнений, называемый методом Гаусса. Его идея состоит в приведении любой системы линейных уравнений с помощью некоторых специальных преобразований, называемых элементарными, к эквивалентной системе некоторого простого вида, все решения которой легко найти. Напомним, что две системы уравнений называются эквивалентными, если множества их решений совпадают, т. е. если каждое решение первой из них является решением второй, и наоборот.
Определение 1. Элементарными преобразованиями системы линейных уравнений называются преобразования следующих трех типов:
1) прибавление к одному уравнению другого, умноженного на число;
2) перестановка двух уравнений;
3) умножение одного уравнения на число, отличное от нуля.
Подчеркнем, что при элементарном преобразовании 1-го типа изменяется только одно уравнение — то, к которому прибавляется другое, умноженное на число.
Очевидно, что всякое решение исходной системы уравнений является решением новой системы, полученной элементарным преобразованием. С другой стороны, исходная система уравнений может быть получена из новой системы подходящим элементарным преобразованием того же типа. Так, если мы прибавим к первому уравнению второе, умноженное на с, то можно вернуться назад, прибавив к первому уравнению новой системы ее второе уравнение (которое такое же, как у исходной системы), умноженное на — с. Поэтому при любом элементарном преобразовании мы получаем систему уравнений, эквивалентную исходной.
Так как нам удобнее работать не с самими системами линейных уравнений, а с их (расширенными) матрицами, дадим соответствующее определение для матриц.
Определение 1′. Элементарными преобразованиями строк матрицы А называются преобразования следующих трех типов:
1) прибавление к одной строке другой, умноженной на число;
2) перестановка двух строк;
3) умножение одной строки на число, отличное от нуля.
Очевидно, что всякое элементарное преобразование системы линейных уравнений приводит к соответствующему элементарному преобразованию ее матрицы коэффициентов и расширенной матрицы.
Покажем теперь, что с помощью элементарных преобразований строк любую матрицу можно привести к достаточно простому виду. Назовем первый отличный от нуля элемент ненулевой строки (a1,a2,…,an) 
Определение 2. Матрица называется ступенчатой, если
1) номера ведущих элементов ее ненулевых строк образуют строго возрастающую последовательность;
2) нулевые строки, если они есть, стоят в конце.
Таким образом, ступенчатая матрица — это матрица вида
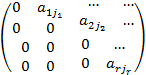
в которой элементы a1j1, а2j2 ,…, arjr, находящиеся в углах ступенчатой линии, отличны от нуля, а все элементы, находящиеся слева и снизу от этой линии, равны нулю. При этом j1 j, и строго треугольной, если, кроме того, аii ≠ 0 при всех i. Система линейных уравнений называется (строго) треугольной, если ее матрица коэффициентов (строго) треугольна.
Рассмотрим теперь произвольную ступенчатую систему линейных уравнений. Пусть число ненулевых строк (число ступенек) ее матрицы коэффициентов равно r, а число ненулевых строк расширенной матрицы равно p. Очевидно, что p = r или r+1.
Возможны следующие три принципиально разных случая.
1-й случай: p = r+1. В этом случае система содержит уравнение вида
где b ≠ 0, и, следовательно, несовместна.
2-й случай: p = r = n. В этом случае после отбрасывания нулевых уравнений получается строго треугольная система. Из ее последнего уравнения однозначно определяется хn, затем из предпоследнего уравнения — xn-1 и т. д. Следовательно, система имеет единственное решение.
Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Метод Гаусса приведения матрицы к ступенчатому виду
Элементарными преобразованиями матрицы называются следующие ее преобразования:
I. Перестановка двух столбцов (строк) матрицы.
II. Умножение всех элементов одного столбца (строки) матрицы на одно и то же число, отличное от нуля.
III. Прибавление к элементам одного столбца (строки) соответствующих элементов другого столбца (строки), умноженных на одно и то же число.
Матрица , полученная из исходной матрицы конечным числом элементарных преобразований, называется эквивалентной . Это обозначается .
Элементарные преобразования применяются для упрощения матриц, что будет в дальнейшем использоваться для решения разных задач.
Покажем, как при помощи элементарных преобразований можно привести матрицу к ступенчатому виду (рис. 1.4). Здесь высота каждой «ступеньки» составляет одну строку, символом 1 (единицей) обозначены единичные элементы матрицы, символом * — обозначены элементы с произвольными значениями, остальные элементы матрицы нулевые. К ступенчатому виду можно привести любую матрицу, причем достаточно использовать только элементарные преобразования строк матрицы .
Видео:Приведение матрицы к ступенчатому виду. Алгоритм ГауссаСкачать

Алгоритм приведения матрицы к ступенчатому виду
Чтобы привести матрицу к ступенчатому виду (рис. 1.4), нужно выполнить следующие действия.
1. В первом столбце выбрать элемент, отличный от нуля ( ведущий элемент ). Строку с ведущим элементом ( ведущая строка ), если она не первая, переставить на место первой строки (преобразование I типа). Если в первом столбце нет ведущего (все элементы равны нулю), то исключаем этот столбец, и продолжаем поиск ведущего элемента в оставшейся части матрицы. Преобразования заканчиваются, если исключены все столбцы или в оставшейся части матрицы все элементы нулевые.
2. Разделить все элементы ведущей строки на ведущий элемент (преобразование II типа). Если ведущая строка последняя, то на этом преобразования следует закончить.
3. К каждой строке, расположенной ниже ведущей, прибавить ведущую строку, умноженную соответственно на такое число, чтобы элементы, стоящие под ведущим оказались равными нулю (преобразование III типа).
4. Исключив из рассмотрения строку и столбец, на пересечении которых стоит ведущий элемент, перейти к пункту 1, в котором все описанные действия применяются к оставшейся части матрицы.
Пример 1.29. Привести к ступенчатому виду матрицы
Решение. В первом столбце матрицы выбираем ведущий элемент . Делим все элементы первой строки на (или, что то же 1 1. самое, умножаем на ):
Прибавим ко второй строке первую, умноженную на (-2):
Первый столбец и первую строку исключаем из рассмотрения. В оставшейся части матрицы имеется один элемент (-2), который выбираем в качестве ведущего. Разделив последнюю строку на ведущий элемент, получаем матрицу ступенчатого вида
Преобразования закончены, так как ведущая строка последняя. Заметим, что получившаяся матрица является верхней треугольной.
В первом столбце матрицы выбираем ведущий элемент . Меняем местами строки, ставя ведущую строку на место первой, и делим элементы ведущей строки на ведущий элемент 2:
Пункт 3 алгоритма делать не надо, так как под ведущим элементом стоит нуль. Исключаем из рассмотрения первую строку и первый столбец. В оставшейся части ведущий элемент — число 2. Разделив ведущую строку (вторую) на 2, получаем ступенчатый вид:
Преобразования закончены, так как ведущая строка последняя.
В первом столбце матрицы выбираем ведущий элемент . Первая строка — ведущая. Делим ее элементы на . Получаем
Ко второй и третьей строкам прибавим первую, умноженную на (-3) и на (-6) соответственно:
Обратим внимание на то, что полученная матрица еще не является матрицей ступенчатого вида, так как вторую ступеньку образуют две строки (2-я и 3-я) матрицы. Исключив 1-ю строку и 1-й столбец, ищем в оставшейся части ведущий элемент. Это элемент (-1). Делим вторую строку на (-1), а затем к третьей строке прибавляем ведущую (вторую), умноженную на 5:
Исключим из рассмотрения вторую строку и второй столбец. Поскольку исключены все столбцы, дальнейшие преобразования невозможны. Полученный вид — ступенчатый.
1. Говорят, что матрица имеет ступенчатый вид также и в случае, когда на месте ведущих элементов (обозначенных на рис. 1.4 единицей) стоят любые отличные от нуля числа.
2. Считается, что нулевая матрица имеет ступенчатый вид.
Пример 1.30. Привести к ступенчатому виду матрицу
Решение. Первый столбец матрицы — нулевой. Исключаем его из рассмотрения и исследуем оставшуюся часть (последние 5 столбцов):
Берем в качестве ведущего элемент . Прибавляем ко второй строке первую, умноженную на (-1); к третьей строке — первую, умноженную на (-2); к четвертой строке — первую, умноженную на (-4). Тем самым «обнуляются» все элементы второго столбца, расположенные ниже ведущего элемента:
Полученная матрица не имеет ступенчатого вида, так как одна из ступенек имеет высоту в три строки. Продолжаем преобразования. Первую строку и второй столбец исключаем из рассмотрения. Поскольку первый столбец в оставшейся части матрицы нулевой, исключаем его. Теперь оставшаяся часть матрицы — это матрица (размеров ), образованная элементами, расположенными в последних трех строках и трех столбцах полученной матрицы. В качестве ведущего элемента выбираем . К третьей строке прибавляем вторую. Получаем матрицу
Вторую строку и четвертый столбец исключаем из рассмотрения. Берем элемент в качестве ведущего. Делим третью строку на число 2 (умножаем на 0,5):
К четвертой строке прибавляем третью, умноженную на (-2):
Третью строку и четвертый столбец исключаем из рассмотрения. Поскольку в оставшейся части матрицы все элементы (один) нулевые, преобразования закончены. Матрица приведена к ступенчатому виду (см. рис. 1.4).
Замечание 1.9. Продолжая выполнять элементарные преобразования над строками матрицы, можно упростить ступенчатый вид, а именно привести матрицу к упрощенному виду (рис. 1.5).
Здесь символом 1 обозначены элементы матрицы, равные единице, символом * — обозначены элементы с произвольными значениями, остальные элементы матрицы нулевые. Заметим, что в каждом столбце с единицей остальные элементы равны нулю.
Пример 1.31. Привести к упрощенному виду матрицу
Решение. Матрица имеет ступенчатый вид. Прибавим к первой строке третью, умноженную на (-1), а ко второй строке третью, умноженную на (-2):
Теперь к первой строке прибавим вторую, умноженную на (-1). Получим матрицу упрощенного вида (см. рис. 1.5):
Замечание 1.10. При помощи элементарных преобразований (строк и столбцов) любую матрицу можно привести к простейшему виду (рис. 1.6).
Левый верхний угол матрицы представляет собой единичную матрицу порядка , а остальные элементы равны нулю. Считается, что нулевая матрица уже имеет простейший вид (при ).
Пример 1.32. Привести матрицу к простейшему виду.
Решение. В качестве ведущего элемента возьмем . Ко второй строке прибавим первую, умноженную на (-2):
Ко второму столбцу прибавим первый, умноженный на (-2), а к третьему -первый, умноженный на (-3):
Умножим все элементы последнего столбца на (-1) и переставим его на место второго:
Таким образом, исходная матрица при помощи элементарных преобразований приведена к простейшему виду (см. рис. 1.6).
Видео:Решение системы уравнений методом ГауссаСкачать

Свойства элементарных преобразований матриц
Подчеркнем следующие свойства элементарных преобразований матриц .
Теорема 1.1 о приведении матрицы к ступенчатому виду . Любую матрицу при помощи элементарных преобразований ее строк можно привести к ступенчатому (или даже упрощенному) виду.
Следствие (о приведении матрицы к простейшему виду). Любую матрицу при помощи элементарных преобразований ее строк и столбцов можно привести к простейшему виду.
1. Преобразования, обратные к элементарным, являются элементарными . В самом деле, если в матрице поменяли местами два столбца (преобразование I типа), то исходную матрицу можно получить, еще раз поменяв местами эти столбцы. Если столбец матрицы умножили на число (преобразование II типа), то для получения исходной матрицы надо этот столбец умножить на обратное число . Если к i-му столбцу матрицы прибавили j-й столбец, умноженный на число , то для получения исходной матрицы достаточно к i-му столбцу матрицы прибавить j-й столбец, умноженный на противоположное число ( ).
2. В теореме 1.1 говорится о приведении матрицы к ступенчатому (упрощенному) виду при помощи элементарных преобразований только ее строк, не используя преобразования ее столбцов. Чтобы привести произвольную матрицу к простейшему виду (следствие теоремы 1.1), нужно использовать преобразования и строк, и столбцов матрицы.
3. Рассмотрим следующую модификацию пункта 3 метода Гаусса. Ведущий элемент, выбранный в п. 1 метода Гаусса, определяет ведущую строку и ведущий столбец матрицы (он находится на их пересечении). Делим все элементы ведущей строки на ведущий элемент (см. п.2 метода Гаусса). Прибавляя ведущую строку, умноженную на соответствующие числа, к остальным строкам матрицы (аналогично п.3 метода Гаусса), делаем равными нулю все элементы ведущего столбца, за исключением ведущего элемента. Затем, прибавляя полученный ведущий столбец, умноженный на соответствующие числа, к остальным столбцам матрицы, делаем равными нулю все элементы ведущей строки, за исключением ведущего элемента. При этом получаем ведущие строку и столбец, все элементы которых равны нулю, за исключением ведущего элемента, равного единице.
Модифицированный таким образом метод Гаусса называется методом Гаусса-Жордана . Его применение позволяет сразу получить простейший вид матрицы, минуя ее ступенчатый вид.
📽️ Видео
11. Ранг матрицыСкачать

15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Приведение определителя к треугольному видуСкачать

Математика без Ху!ни. Метод Гаусса.Скачать

Ранг матрицыСкачать

12. Метод Гаусса решения систем линейных уравнений. Часть 1.Скачать

Приведение матрицы к ступенчатому видуСкачать

Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

§16 Приведение определителей к треугольному видуСкачать

Решение системы уравнений методом Гаусса 4x4Скачать

Ранг матрицыСкачать

Алгоритм приведения матрицы к треугольному видуСкачать
Лекция 13. Исследование систем линейных уравнений. Теорема Кронекера — Капелли.Скачать

Решение системы уравнений методом Крамера.Скачать

Решение системы уравнений методом Гаусса. Бесконечное множество решенийСкачать