Методы теории подобия позволяют преобразовать ДУ Навье-Стокса, описывающие движение реальной жидкости, и получить общую функциональную зависимость между критериями ГД подобия, характеризующими силы, действующие при движении жидкости.
Уравнение Навье-Стокса для практических случаев решить чисто математически невозможно.
Преобразуем уравнение Навье-Стокса для оси OZ в соответствии с положениями теории подобия.
1. Отбрасываем знаки дифференциала;
2. Считаем геометрический размер z=l (линейным)
Для установившегося режима отсутствуют изменения технологической переменной во времени, поэтому в левой части уравнения заменяем отношение дифференциалов на отношение конечных величин.
3. Делим все слагаемые на ρ
4. Учитывая, что время может быть выражено
5. Делим правую часть на левую
Отражает влияние силы тяжести на движение жидкости и характеризует отношение сил инерции к силе тяжести в подобных потоках.
Это отношение сил давления к силе инерции. Отражает влияние перепада гидростатического давления на давление жидкости.
Отражает влияние силы трения на движение жидкости.
Помимо этих критериев имеет место:
Критерии Рейнольдса, Фруда и гомохромности составлены из величин определяющих распределение скоростей в потоке, и поэтому являются определяющими критериями ГД подобия.
Критерий Эйлера включает в себя абсолютное давление, которое нужно определить, т.к. если знать разность – известна движущая сила, поэтому он является определяемым критерием.
Т.о., чтобы процессы, происходящие в модели и в натуре, были подобны в сходных точках, должно осуществляться равенство:
Согласно второй теории подобия, критерии подобия должны быть связаны между собой критериальным уравнением:
Необходимо учитывать симплекс геометрического подобия.
Любую функциональную зависимость можно описать степенной функцией
Путем обработки опытных данных на моделях находят численные значения коэффициента А и степеней m,n,r,q и получают обобщенное критериальное уравнение ГД для данного процесса.
Если процесс установившийся:
При турбулентном движении капельных жидкостей и газов, перемещаемых с помощью насосов и компрессоров, влияние силы тяжести на распределение скоростей и перепад давления незначительно, поэтому Fr может быть исключен:
Некоторые физические величины, входящие в критерии подобия, целесообразно заменять на другие им пропорциональные, т.к. иногда бывает почти невозможно экспериментально определить ту или иную физическую величину, входящую в критерий подобия; поэтому используются производные от остальных критериев подобия.
Т.о. получают критерий подобия для естественной конвекции, т.е. движении, возникающем вследствие разности плотностей
Критериальное уравнение подобия процесса можно получить, используя метод анализа размерностей.
Один из методов обработки экспериментальных данных с получением критериального уравнения – π – теорема Бекингема, согласно которой общая функциональная зависимость, связывающая между собой n переменных величин при m основных единицах измерения может быть представлена в виде зависимости между (n-m) безразмерных комплексов этих величин, а при наличии подобия в виде связи между этим количеством критериев подобия.
Видео:Теорема Безу. 10 класс.Скачать

Пи-теорема Букингема
Определение типа этой зависимости возможно только путем экспериментов и требует большого количества экспериментов. Анализируя размеры стенда, можно уменьшить количество экспериментов, необходимых для решения поставленной задачи. Во-первых, давление (то есть величина падения давления, вызванного движением) рассчитывается по формуле (14. 21) предполагает, что это зависит от переменных. Это предположение основано на предварительных признаках физики phenomenon. It не всегда заранее понятно, какие переменные следует учитывать. Метод Бекингема основан на предположении, что уравнения, описывающие поведение системы, должны иметь равномерные размеры, поэтому уравнение.
Может быть записана в безразмерную переменную с помощью процедуры, аналогичной процедуре, используемой для вывода. Символ L обозначает безразмерную переменную и описывает этот результат в общем виде. «, = / («Я».). (14.22) Где формула(14. 21) (14. 22).Сюда входят только безразмерные переменные. Во-первых, формула(14. 21) Сколько получается безразмерных комплексов, то есть должно быть установлено значение r. Это значение определяется отношением. / = н-р, (14.23) Где n-число переменных. g-максимальное число переменных, в которых невозможно сформировать безразмерную комбинацию (значение g обычно равно числу базовых измерений).
Для рассматриваемой общей задачи формула(14. 21) от η= 8 выбор, вы можете видеть, что любая комбинация A, u и o не является безразмерной quantity. To проиллюстрируйте это, запишите такую комбинацию в следующем виде По (> ы(14.24) И затем мы заменяем каждую переменную на это измерение.: (14-25) M находится только в измерении p, T — только в измерении, и даже если выбрать значения a, b, c, то выражение(14. 25) не может быть безразмерным. Одно из оставшихся значений переменной(14. 25) найти значение индикатора, которое будет принято, как только будет показана формула без измерения. r = 3, поэтому он должен быть равен 5. Существует 5 независимых безразмерных групп NN n2, фунт. 1.
Интересное обсуждение этого вопроса было дано Бриджменом [14], а также размерным анализом в целом. Эффекты гравитации — это 1-эффекты поверхностного натяжения o, 1-быстрый C, 1-Давление p, связанные с эффектами. Поэтому мы выбираем безразмерную комбинацию так, чтобы каждая из переменных p, a, C и p входила только в 1 группу. С другой стороны, А и Р могут влиять практически на любой процесс, поэтому их присутствие допустимо в любом комплексе. напишите Л1 14.
- Форма этого уравнения, выраженная в 3 основных измерениях, является (14. Двадцать семь). Показатель степени переменной должен быть безразмерным в этом выражении. Это требует удовлетворения системы уравнений М, Б, Т 0 = с -> -^; 0 = а 4-Б-3С-о = — б-2а (14. Двадцать восемь) (14. 29.) (14. Тридцать) Решая эти уравнения, можно выразить все показатели любым из них. установите g и получите b =-2(1, c = — a и a = 0.Далее, формула(14. 22) содержит все неизвестные функции ETA, поэтому вы можете выбрать показатель C1, равный 1. = = Ec-это число Эйлера. Положите его в L2 (если R = −1) l2 = — число Рейнольдса, r * (14. Тридцать одна) (14. Тридцать два)14.
Аналогично, формула(14. 26) и (14. 32) заменяя 4-ю переменную последовательно на C и o, получим оставшуюся безразмерную величину l. As итог L3 = — = Er-число флюида. l4 =и/ C = M-число Маха. 55 =22Л / a = Ye — это число Вебера. (14.34)) (14. Тридцать пять) (14. Тридцать шесть) Уравнение для этой задачи (14.21) имеет вид: Она= /(та, ТМ, м, Ауэ). (14. Тридцать семь) Такая система из 5 безразмерных комплексов называется полной. Каждый из них зависит от другого.
Многие другие безразмерные переменные, например、 NeKg = 7? (14.38) Именно этот комплекс может помочь в изучении некоторых специальных проблем. К счастью, во многих случаях уравнение(14. 37) некоторые термины представляют собой незначительное воздействие. Вы можете упомянуть следующие проблемы, но некоторые из них были изучены аналитически в предыдущих главах. 1.Идеальное движение жидкости.
Это приближение может быть применено к расчетам производительности подъема профиля или вентилятора, если эффекты вязкости, силы тяжести, поверхностного натяжения и сжимаемости (число Маха) являются negligible. In в этом случае формула(14. 37) принимает вид: ЕІ = — ^ — = НБР, (14.39) Что можно считать модификацией уравнения Бернулли. 2.Если требуется только вязкое сопротивление, то поток в трубе или поток вокруг объекта, погруженного в жидкость. (14.40)) (Напомним, что это эквивалентно co или/.)Для обтекания цилиндра формула(14. 15) представляет собой формулу (14. Двадцать) ^ = / х(быть).
Для течения в гладкой трубе формула(13. 67) определяется коэффициентом сопротивления/. Ра _ _ / I2rL и 2P 2 Формула (7. 10) от、 м Уравнение / принимает вид 13. 8.Одежда. Они формируются уравнениями, поэтому нужно ввести количество флейт. Ра. 4.Быстрая езда. Барри в т и А. (14. Сорок один) График зависимостей/ 3.Поток вокруг поверхностной волны、 __ri8 (14.42) Ф(М / с). RL Для этого типа задач, необходимо usech. 17. 5.Движение распадающихся взвешенных частиц. (14.43).




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Теорема Виета для многочлена 3 порядка. 10 класс.Скачать

Основы теории подобия. Анализ размерностей. Теорема Бекингема.
Читайте также:
|
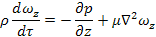
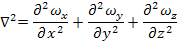
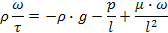
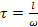
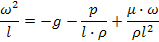
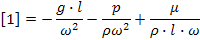
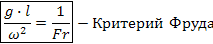
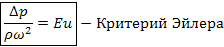
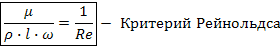
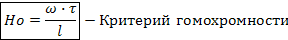
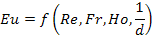
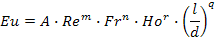
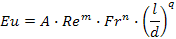
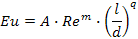

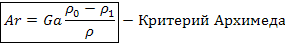







 .
.
 (17), где P1 и P2 — гидростатическое давление в сечениях 1-1 и 2-2.
(17), где P1 и P2 — гидростатическое давление в сечениях 1-1 и 2-2. где Wr – скорость движения жидкости вдоль оси (18) , цилиндра на расстоянии r от оси.
где Wr – скорость движения жидкости вдоль оси (18) , цилиндра на расстоянии r от оси. (19). После подстановки и сокращения переменных, получим выражение для
(19). После подстановки и сокращения переменных, получим выражение для  (20)
(20) .
.
 (22)
(22)



















