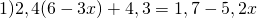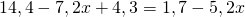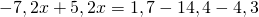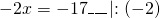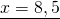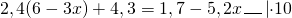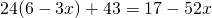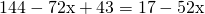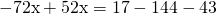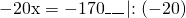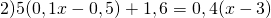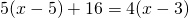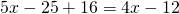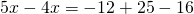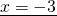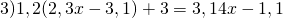Тема уравнения с десятичными дробями

Видео:Как решать уравнения с десятичными дробями - математика 5 классСкачать

Уравнения с десятичными дробями

Линейные уравнения с десятичными дробями можно решать так же, как и остальные линейные уравнения.

Однако, удобнее сначала уравнение упростить, избавившись от десятичных дробей.

Для начала рассмотрим оба способа решения и сравним их.

Раскрываем скобки. Так как перед скобками стоит множитель, умножаем этот множитель на каждое слагаемое в скобках:

Это — линейное уравнение. Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:

Обе части уравнения делим на число, стоящее перед иксом:

Чтобы перевести десятичные дроби в целые числа, умножим обе части уравнения почленно на 10:

(При умножении произведения 2,4(6-3х) на 10 применяем сочетательное свойство умножения, то есть на 10 мы умножим только первый множитель, 2,4).

Получили линейное уравнение, которое не содержит десятичных дробей. Решаем его:

На мой взгляд, линейные уравнения с десятичными дробями удобнее решать, переводя их в уравнения с целыми числами.

Чтобы избавиться от десятичных дробей, обе части уравнения умножаем на 10. При этом в произведении 5(0,1х-0,5) на 10 умножаем второй множитель, то есть выражение в скобках, а в произведении 0,4(х-3) — первый, то есть 0,4:

Далее — решаем обычное линейное уравнение:

Обе части уравнения умножаем на 100. При этом в произведении 1,2(2,3х-3,1), надо первый множитель 1,2 умножить на 10 и второй множитель (2,3х-3,1) умножить на 10:

Видео:Уравнения с десятичными дробями в 5 классе (на умножение и деление).Скачать

Решение уравнений с дробями

О чем эта статья:

5 класс, 6 класс, 7 класс

Видео:Уравнения с десятичными дробями. Математика 5 классСкачать

Понятие дроби

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:

• обыкновенный вид — ½ или a/b,
• десятичный вид — 0,5.

Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.

Дроби бывают двух видов:

1. Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
2. Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.

Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.

Видео:Уравнения с десятичными дробями в 5 классе (на сложение и вычитание).Скачать

Основные свойства дробей

Дробь не имеет значения, если делитель равен нулю.

Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.

Дроби a/b и c/d называют равными, если a × d = b × c.

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.

Видео:Уравнение. 5 класс.Скачать

Понятие уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:

• Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
• Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Решить уравнение значит найти все его корни или убедиться, что корней нет.

Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.

Видео:Уравнение на десятичные дроби со скобками и делением. Номер 391г.Скачать

Понятие дробного уравнения

Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:

Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.

Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:

На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.

Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.

Видео:Решение уравнений, 6 классСкачать

Как решать уравнения с дробями

1. Метод пропорции

Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.

Итак, у нас есть линейное уравнение с дробями:

В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.

После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.

2. Метод избавления от дробей

Возьмем то же самое уравнение, но попробуем решить его по-другому.

В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:

• подобрать число, которое можно разделить на каждый из знаменателей без остатка;
• умножить на это число каждый член уравнения.

Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!

Вот так просто мы получили тот же ответ, что и в прошлый раз.

Что еще важно учитывать при решении

• если значение переменной обращает знаменатель в 0, значит это неверное значение;
• делить и умножать уравнение на 0 нельзя.

Универсальный алгоритм решения

Определить область допустимых значений.

Найти общий знаменатель.

Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.

Раскрыть скобки, если нужно и привести подобные слагаемые.

Решить полученное уравнение.

Сравнить полученные корни с областью допустимых значений.

Записать ответ, который прошел проверку.

Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.

Видео:УРАВНЕНИЯ С ДЕСЯТИЧНЫМИ ДРОБЯМИ. Примеры | МАТЕМАТИКА 6 классСкачать

Примеры решения дробных уравнений

Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.

Пример 1. Решить дробное уравнение: 1/x + 2 = 5.

1. Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
2. Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
3. Избавимся от знаменателя. Умножим каждый член уравнения на х.

Решим обычное уравнение.

Пример 2. Найти корень уравнения

1. Область допустимых значений: х ≠ −2.
2. Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
3. Избавимся от знаменателя. Умножим каждый член уравнения на х.

Переведем новый множитель в числитель..

Сократим левую часть на (х+2), а правую на 2.

Пример 3. Решить дробное уравнение:

Найти общий знаменатель:

Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:

Выполним возможные преобразования. Получилось квадратное уравнение:

Решим полученное квадратное уравнение:

Получили два возможных корня:

Если x = −3, то знаменатель равен нулю:

Если x = 3 — знаменатель тоже равен нулю.

Видео:Уравнение с десятичными дробямиСкачать

Разработка урока математики по теме «Решение уравнений с десятичными дробями»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Изучаемая тема: Действия над десятичными дробями

Тема урока: Решение уравнений, содержащих десятичные дроби.

Цели урока: 1) повторение и систематизация правил выполнения действий над десятичными дробями и правил нахождения неизвестных компонент арифметических действий;

2) развитие творческого мышления,

умения рассуждать, анализировать;

развитие культуры математической

речи, навыков общения и говорения;

4) овладение навыками сбережения своего физического и психического здоровья.

Тип урока: урок отработки умений и навыков

Используемая Развивающего обучения

Итак, ребята, встали, показали готовность к уроку: у вас на парте лежит все необходимое для работы. Садитесь!

Сядьте удобно, закройте глаза, сделайте три глубоких вдоха. Подумайте о том, что у каждого из вас есть прекрасная возможность добиться успеха. Предлагаю вам вдуматься в слова немецкого писателя и ученого Георга Лихтенберга (записаны на доске) : «Слово трудность не должно существовать для творческого ума!»

Откройте глаза и скажите: каким вы хотите видеть сегодняшний урок? ( ответы детей: интересным, увлекательным, легким и т. д.) Я согласна с вами и желаю, чтобы урок получился творческим.

Десятичные дроби, с которыми мы работали последнее время, сегодня являются героями уравнений. Поэтому наш урок называется: “ Решение уравнений, содержащих десятичные дроби ” (дети читают на доске)

Какие же знания нам понадобятся на уроке? Мы должны знать (дети читают на доске) :

что такое уравнение;

что значит решить уравнение;

правила нахождения неизвестных компонент арифметических действий ( ученикам предлагается конкретизировать этот вопрос);

правила выполнения арифметических действий над десятичными

дробями ( ученикам предлагается ответить, о каких действиях идет речь).

Таким образом, сегодня нам понадобятся знания по темам «Уравнение» и «Десятичные дроби» ( на табло появляются названия этих двух тем ).

Видео:ДЕЛЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ 😉 #егэ #егэ #математика #профильныйегэ #shorts #образованиеСкачать

III . Актуализация теоретических знаний.

Проверим знание правил нахождения неизвестных компонент .

1 ученик с использованием данного набора карточек на наборном полотне составляет указанные правила .

Решение уравнений не будет успешным, если мы будем ошибаться при вычислениях. На этой части доски вы видите три уже решенных примера. Верно ли они решены?

2ой ученик работает у доски .

Помните, ребята, на прошлых уроках мы выполняли задания, позволяющие нам получить дополнительные сведения из истории математики. Так, мы узнали о математике, у которого способности раскрылись в возрасте трех лет. Это… (дети называют имя Гаусса) . Знакомо нам имя математика с очень трудной судьбой: он ослеп будучи еще ребенком. Это … (дети называют имя Потрягина) . Сегодня мы знаем и решаем уравнения благодаря …. ( учащимся знакомо имя Диофанта ).
А вот кто придумал десятичные дроби? Найти ответ на этот вопрос поможет нам пример ( запись на доске ):

Варианты ответа : 209,42 – Архимед; 13,7 – аль- Коши;

Выполнять эту задачу доверим “пятерке”: …. (называются имена учеников). Успехов вам! А мы ждем результат.

Для остальных в это время вычислительная разминка :

56 + 27 29 3 76 : 4 7,5 – 5

80 – 54 18 6 65 : 5 1,1 0,4

По окончании разминки проверяется работа 1-ого ученика по составлению правил нахождения неизвестных компонент.

Его результат (в случае ошибок исправленный) помещается в “конспект” урока.

Работа над ошибками второго ученика проверяется с помощью набора карточек с вариантами ответов, на обороте которых + или – (верно или неверно).

Спросим сейчас у нашей отважной “пятерки”, кто придумал десятичные дроби? ( ответ )

Итак, благодаря Диофанту и аль-Коши возможен наш урок. (на табло рядом со словами “уравнение”, “десятичные дроби” появляются “Диофант”, “ аль-Коши”).

верно – руки вперед, пошевелить пальцами;

неверно – наклоны головы вправо-влево.

36 + 16 = 52 ; 3 0 = 0; 44 + 0 = 44;

27 – 8 = 21; 15 : 15 = 0; 9 6 = 63.

Упражнение для глаз:

Крепко зажурить глаза на 3 секунды. Повторить 6 раз. Далее 4 раза движение глаз по кругу в одну и другую сторону.

В течение 20 секунд поморгать веками, а затем закрыть глаза.

Упражение на концентрацию внимания внимания: смотреть на точку, расположенную на доске в течение 30 секунд.

Y . Практикум по решению уравнений.

Итак, все необходимое для решения уравнений повторили, вспомнили. Переходим к основной части — решению уравнений. Будем двигаться от простого к сложному.

Посмотрим на уравнение 2х = 4. Вы можете назвать его корень? ( заслушиваются различные мнения, ответ обосновывается)

2)Уравнение 2х = 1 . Его корень? Выскажите свое мнение, указав на правило, которое применили.

Таким образом, решение уравнения не должно происходить наугад, оно не должно быть формальным. Чтобы избежать ошибки, мы должны решать, рассуждая, опираясь на правила.

Вот знакомая нам схема рассуждений ( см. опорную схему “Решение уравнений на основе зависимости между компонентами арифметических действий”; помещается в “конспект” урока)

3) На примере уравнений покажем, как работает указанная схема рассуждений ( фронтальная работа ):

Сейчас предлагаю каждому испыпать свои силы и возможности в самостоятельном решении уравнений. Объявляю небольшой практикум. Пусть девизом станут слова: “Решил – покажи, не знаешь или сомневаешься – спроси”:

YI . Подведение итогов и рефлексия. Домашнее задание.

Сегодня каждый из вас ставил цель – попрактиковаться в решении уравнений с десятичными дробями, повторив для этого необходимые теоретические вопросы. Что же вы можете сказать по этому поводу? Как достигнута вами эта цель ? Довольны ли вы своей работой? (учащиеся по желанию высказывают своё мнение, ставят ближайшие цели) . Получился ли наш урок увлекательным, интересным, легким, каким вы хотели его видеть в начале? …

Я считаю, что наш урок получился творческим, он состоялся благодаря нашей совместной работе. Называю результаты

Оценивание за работу на уроке , домашнее задание.

Урок математики в 8 классе

Анализ ошибок контрольной работы по теме «Дробные рациональные уравнения». Числовые неравенства. (2 урока)

Образовательные.
Учащиеся должны знать:
1) алгоритм решения дробных рациональных уравнений;
2) определение сравнения чисел;
Учащиеся должны уметь:
1) решать дробные рациональные уравнения и с их помощью задачи;
2) применять определение сравнения чисел при решении задач.

Развивающие.
Способствовать формированию математической речи учащихся, развитию внимания, памяти, активизации мыслительных операций (анализ, сравнение, выделение главного, алгоритмизация).

Воспитательные.
Создать условия для воспитания чувства ответственности за выполняемую работу, дисциплинированности, умения слушать других и анализировать результаты собственной деятельности, для привития здоровьесберегающих навыков.

Мотивационный этап. Целеполагание.

Каким вы хотите видеть наш урок? (ответы учащихся). Я хочу, чтобы урок принес вам удовлетворение, радость приобретения новых знаний и радость избавления от неудач прошлых. Это значит, что нас сегодня ждет изучение нового материала и работа над ошибками прошлого урока.

Подтверждает ли тема урока сказанные мною слова? (учащиеся читают тему урока).

Давайте заглянем в «конспект» ( на обороте доски опорные схемы «Решение дробных рациональных уравнений», «Неполные квадратные уравнения», « Решение квадратных уравнений», «Числовые неравенства. Определение», «Числовые неравенства. Свойства» ). Что нового ? ( мнение учеников ).
Обратите внимание на центральную часть доски… ( учащиеся замечают, что их ждут новые примеры-образцы )

Где могут пригодиться новые знания. Зачем нужны уравнения? ( мнение учащихся )

Решение некоторых текстовых задач сводится к решению неравенств.

Итак, определили цели, план работы на предстоящих сегодня 2 урока.

Работа над ошибками контрольной работы.

Сегодня мы говорим о результатах прошедшей контрольной работы. Они вас устраивают? ( рефлексия результатов контрольной работы ). Я рада, что вы не хотите останавливаться на достигнутом.

1) Проговор вслух алгоритма решения дробных рациональных уравнений по опорной схеме.

Анализ типичных ошибок .

Согласны ли вы с предложенным фрагментом решения уравнения:

;

;

;

Укажите правильный вариант ответа в следующем примере

:

1) –20; 2) –7; 3) нет верного ответа.

Индивидуальная работа под контролем учителя . (10 мин)

( см. приложение, задания для индивидуальной работы)

У вас на парте лежит карточка с 5 заданиями, № 1, 2, 4 которой аналогичны заданиям контрольной работы. Сделайте выбор с учетом допущенных ошибок. Подсказка: ответы в № 1-4 записаны с помощью цифр от 1 до 8, которым соответствуют имена известных математиков. Таким образом, работа с предложенными заданиями поможет нам получить дополнительную информацию: кто был первооткрывателем уравнений?
1) Диофант 5) Пифагор

2) Аристотель 6) Архимед

Декарт 8) Аль-Хорезми

Работаем по принципу: «Реши – покажи, не знаешь – спроси. Не бойся ошибиться – бойся промолчать».

( По окончании работы – заслушивание результатов, самооценка работы, рефлексия )

На контрольной работе вам была предложена задача на движение. Неправильная и неграмотная работа с условием привела многих к неверному результату. Есть ли на доске фрагмент, показывающий как удобно работать с условием в задачах на движение?

Учащиеся указывают на макет таблицы и озвучивают название ее столбцов:

Предлагаю поработать в группах и выполнить следующее задание (см. приложение, задания для групповой работы).

( По окончании – заслушивание результатов, подведение итогов, рефлексия ).

Изучение нового материала.

Знакомо ли вам слово «неравенство»? С чем вы его ассоциируете? (учащиеся указывают на слово «сравнение» ). Действительно, в младших классах вам приходилось решать примеры на сравнение чисел. Помните ли вы изученные правила?

10070 * 1009
4,7971 * 5,1

*

В зависимости от конкретного вида чисел мы используем то или иное правило сравнения. Однако удобно иметь такой универсальный способ сравнения, который охватывает все случаи. Заглянем в «конспект урока».

( работа с определением сравнения чисел: учащимся предлагается озвучить математическую запись )

Зачем новый способ сравнения чисел, где он может быть применен?

а) Сравните .
б) Сравните .

. Верно ли?

Верно ли ?

Что нового узнали? Где могут пригодиться новые знания?

🎬 Видео

КАК РЕШИТЬ УРАВНЕНИЕ С ДЕСЯТИЧНЫМИ ДРОБЯМИ? Примеры | МАТЕМАТИКА 5 классСкачать

Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Решение уравнений с десятичными дробямиСкачать

Сложные уравнения со скобками. Как решать уравнения в несколько действий в 5 классе.Скачать

Решение уравнений ( подобные слагаемые ) . 6 класс .Скачать

Пропорция. Основное свойство пропорции. Практическая часть - решение задачи. 2 часть. 6 класс.Скачать

Действия с десятичными дробями 😈Скачать

Все действия с десятичными дробями (Сложение, вычитание, деление и умножение)Скачать

Уравнения с дробями. Как решать уравнения с дробями в 5 классе.Скачать

522 Математика 6 класс. Решим уравнение с десятичными дробямиСкачать