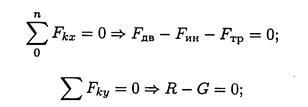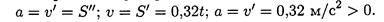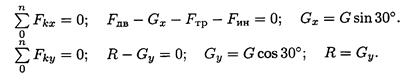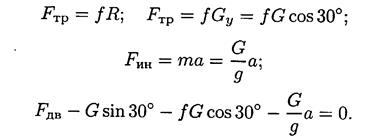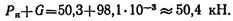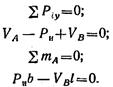Активные силы: движущая сила, сила трения, сила тяжести. Реакция в опоре R. Прикладываем силу инерции в обратную от ускорения сторону. По принципу Даламбера, система сил, действующих на платформу, становится уравновешенной, и можно составить уравнения равновесия. Наносим систему координат и составляем уравнения проекций сил.
где .Fдв — движущая сила;
G — сила тяжести; R — реакция опоры;
Fин — сила инерции; f — коэффициент трения.
Пример 2.Тело весом 3500 Н движется вверх по наклонной плоскости согласно уравнению
S= 0,16 t 2 (рис. 14.5). Определить величину движущей силы, если коэффициент
трения тела о плоскость f = 0,15.
1. Составим расчетную схему, выберем систему координат с осью Ох вдоль наклонной плоскости.
Активные силы: движущая, сила трения, сила тяжести. Наносим реакцию в опоре перпендикулярно плоскости. Чтобы верно направить силу инерции, необходимо знать направление ускорения, определить это можно по уравнению движения.
При а > 0 движение равноускоренное.
2. Определяем ускорение движения:
Силу Fин направим в обратную от ускорения сторону.
3. По принципу Даламбера составим уравнения равновесия:
4. Подставим все известные величины в уравнения равновесия: .
Выразим неизвестную силу и решим уравнение:
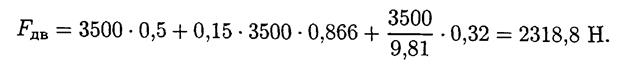
Видео:Движение тела вверх и вниз по наклонной плоскости с учётом тренияСкачать

Принцип кинетостатики (принцип Даламбера)
Принцип кинетостатики используют для упрощения решения ряда технических задач. Реально силы инерции приложены к телам, связанным с разгоняющимся телом (к связям).
Даламбер предложил условно прикладывать силу инерции к активно разгоняющемуся телу. Тогда система сил, приложенных к материальной точке, становится уравновешенной, и можно при решении задач динамики использовать уравнения статики.
Принцип Даламбера:
Материальная точка под действием активных сил, реакций связей и условно приложенной силы инерции находится в равновесии:
Порядок решения задач с использованием принципа Даламбера
- Составить расчетную схему.
- Выбрать систему координат.
- Выяснить направление и величину ускорения.
- Условно приложить силу инерции.
- Составить систему уравнений равновесия.
- Определить неизвестные величины.
Примеры решений задач
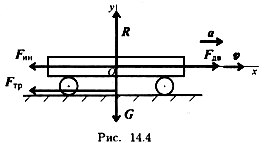
Решение
Активные силы: движущая сила, сила трения, сила тяжести. Реакция в опоре R. Прикладываем силу инерции в обратную от ускорения сторону. По принципу Даламбера, система сил, действующих на платформу, становится уравновешенной, и можно составить уравнения равновесия. Наносим систему координат и составляем уравнения проекций сил.
 |
где Frb — движущая сила; Fтр – сила трения; G — сила тяжести; R — реакция опоры; Fmi — сила инерции; f — коэффициент трения.
Пример 2. Тело весом3500 Н движется вверх по наклонной плоскости согласно уравнению S =0,16t 2 (рис.14.5). Определить величину движущей силы, если коэффициент трения тела о плоскость f=0,15.
Решение
1. Составим расчетную схему, выберем систему координат с осью Ох вдоль наклонной плоскости.
Активные силы: движущая, сила трения, сила тяжести. Наносим реакцию в опоре перпендикулярно плоскости. Чтобы верно направить силу инерции, необходимо знать направление ускорения, определить это можно по уравнению движения.
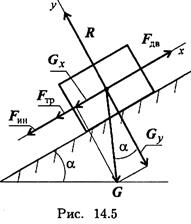
2. Определяем ускорение движения:
a = v’ = S»; v = S’ = 0,32t; a = v’ = 0,32 м/с 2 > 0.
Силу Fин направим в обратную от ускорения сторону.
3. По принципу Даламбера составим уравнения равновесия:
4. Подставим все известные величины в уравнения равновесия:
Выразим неизвестную силу и решим уравнение:

Пример 3. График изменения скорости лифта при подъеме известен (рис. 14.6). Масса лифта с грузом 2800 кг. Определить натяжение каната, на котором подвешен лифт на всех участках подъема.
Решение
1. Рассмотрим участок 1 — подъем с ускорением. Составим схему сил (рис. 14.7). Уравнение равновесия кабины лифта:
где Т — натяжение каната; G — сила тяжести; FИH — сила инерции, растягивающая канат.
Для определения ускорения на участке 1 учтем, что движение на этом участке равнопеременное, скорость v = vo + at; v0 = 0. Следовательно, ускорение:
Определяем усилие натяжения каната при подъеме с ускорением
T1 = 2800(9,81 + 1,25) = 30968H; T1 = 30,97кН.
2. Рассмотрим участок 2 — равномерный подъем.
Ускорение и сила инерции равны нулю. Натяжение каната равно силе тяжести.
3. Участок 3 — подъем с замедлением.
Ускорение направлено в сторону, обратную направлению подъема. Составим схему сил (рис. 14.8).
Уравнение равновесия: FИН3 + Т3 — G = 0. Отсюда
Ускорение (замедление) на этом участке определяется с учетом того, что v = 0.
Натяжение каната при замедлении до остановки:
Т3 = 2 800 ^9,81 — 0 = 25 144 Н; Г3 — 25,14 кН.
Таким образом, натяжение каната меняется при каждом подъеме и опускании, канат выходит из строя в результате усталости материала. Работоспособность зависит от времени.
Пример 4. Самолет выполняет «мертвую петлю» при скорости 160 м/с 2 , радиус петли 1000 м, масса летчика 75 кг. Определить величину давления тела на кресло в верхней точке «мертвой петли».
1. Схема сил, действующих на летчика (рис. 14.9):
гдеG — сила тяжести,R— реакция в опоре, FИН п — сила инерции.
Сила давления летчика на кресло равна силе давления опоры на летчика.
Уравнение равновесия (движение равномерное по дуге, действует только нормальное ускорение): F»H — G — R = 0;

Решение
Активной силой, действующей на рамку, является сила тяжести груза
Освободив^ рамку от связей, прикладываем к ней реакции опор VА и VВ (рис. 1.61,6).
Мысленно остановив рамку, прикладываем к ней в точке крепления груза центробежную силу инерции
Так как рамка вращается равномерно, касательное ускорение груза равно нулю и полное его ускорение равно нормальному. Соответственно полная сила инерции равна центробежной силе инерции груза.
Нормальное ускорение направлено к оси вращения, сила инерции — противоположно (рис. 1.61,6).
 |
Определим величину нормального ускорения:
Сила инерции и сила тяжести в заданном положении груза суммируются:
В данном случае сила тяжести значительно меньше силы инерции и, вообще говоря, можно было бы силой тяжести пренебречь.
Составляя уравнения равновесия

Решение
Добавочные динамические реакции VА и Vв опор балки возникнут от силы инерции груза
Сила инерции направлена вниз, так как ускорение груза направлено вверх.
Освобождаем балку от связей и заменяем их действие реакциями VА и Vв.
Составляем уравнения равновесия:
Решая уравнения, находим:
Контрольные вопросы и задания
1. Объясните разницу между понятиями «инертность» и «сила инерции».
2. 
3. В чем заключается принцип кинетостатики?
4. Задано уравнение движения материальной точки S = 8,6 t 2 . Определите ускорение точки в конце десятой секунды движения.
5. Тело движется вниз по наклонной плоскости (рис. 14.10). Нанесите силы, действующие на тело; используйте принцип Даламбера, запишите уравнение равновесия.
6. 
7. Автомобиль въезжает на арочный мост с постоянной скоростью v (рис. 14.12). Нанесите силы, действующие на автомобиль в середине моста, используя принцип кинетостатики, запишите уравнения равновесия.
Работа и мощность при поступательном движении
Видео:Тело массой 3 кг под действием силы F перемещается вниз по наклонной плоскости на - №22984Скачать

Условие задачи
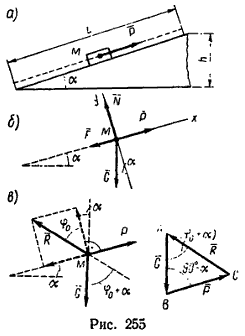
Тело М весом G=50 кГ равномерно перемещается вверх по наклонной плоскости, длина которой l=4 м и угол подъема α=20° (рис. 255, а). Определить работу, производимую силой, направленной параллельно наклонной плоскости, и коэффициент полезного действия наклонной плоскости. Коэффициент трения f=0,2.
Видео:Тело массой 2 кг под действием силы F перемещается вверх по наклонной плоскости на - №22978Скачать

Решение 1
1. При движении тела М (примем его за материальную точку) вверх по наклонной плоскости на него действуют четыре силы: вес G, нормальная реакция наклонной плоскости N, движущая сила Р и сила трения F (рис. 255, б).
2. Работа силы Р при перемещении тела по длине наклонной плоскости
A = Pl.
3. Найдем необходимую для перемещения тела М силу Р.
Расположив оси координат, как показано на рис. 255, б, составим два уравнения равновесия:
(1) ∑ Xi = 0; P — G sin α — F = 0;
(2) ∑ Yi = 0; N — G cos α = 0.
Дополним эти уравнения третьим уравнением, выражающим основной закон трения:
(3) F = fN.
Из уравнения (1)
P = G sin α + F.
Вместо силы трения F подставим ее значение из уравнения (3):
P = G sin α + fN,
а вместо нормальной реакции N подставим ее значение из уравнения (2):
P = G sin α + fG cos α = G(sin α + f cos α).
4. Следовательно, работа силы P
А = Gl(sin α + f cos α).
После подстановки в это уравнение числовых значений
A = 50*4(sin 20° + 0,2 cos 20°) = 106 кГ*м.
Для перевода в СИ достаточно умножить на ускорение свободного падения g=9,81 м/сек 2 .
5. Находим к. п. д. наклонной плоскости:
η = Aпол/A.
Полезная работа состоит в подъеме тела весом G на высоту h=l sin 20°, поэтому
η = Aпол/A = (Gl sin 20°)/A = (50*4*sin 20°)/106 = 0,644.
Видео:ЕГЭ Физика Задание 4 #11261Скачать

Решение 2
1. Можно считать, что на тело М действуют не четыре, а три силы: G – вес тела, движущая сила Р и полная реакция поверхности реальной связи R, равная геометрической сумме сил N и F (рис. 255, в).
Реакция реальной связи R, как известно (§ 15), при движении отклоняется от нормали к поверхности связи на величину угла трения φ0, причем tg φ0=f, где f – коэффициент трения.
2. Так как на тело М действуют только три силы и они образуют уравновешенную систему (тело М, принятое за материальную точку, движется равномерно и прямолинейно), силовой треугольник ABC, построенный из этих сил, является замкнутым.
3. По рис. 255, в можно определить, что в силовом треугольнике ABC угол B=90°-α, угол A=φ0+α. Следовательно,
∠C = 180° — (∠B + ∠A) = 180° — (90° — α + φ0 + α) = 90° — φ0.
Видео:Вес тела. Практическая часть - решение задачи. 7 класс.Скачать

Решение 3
1. Известно, что при действии на точку нескольких сил алгебраическая сумма работ всех сил на некотором пути равна работе равнодействующих этих сил (Е. М. Никитин, § 83).
2. В данном случае на тело М, которое примем за материальную точку, действуют четыре силы: вес G, нормальная реакция наклонной плоскости N, сила трения F и движущая сила Р (см. рис 255, б).
3. Точка М движется равномерно и прямолинейно. Равнодействующая сил, действующих на точку, равна нулю, и, следовательно, алгебраическая сумма работ, производимых силами G, N, F и Р на длине l наклонной плоскости, также равна нулю:
AG + AN + AF + AP = 0.
4. Находим отсюда работу силы Р:
(а) AP = -(AG + AN + AF),
где работа силы G
AG = Gl cos (90° + α) = -Gl sin α
работа силы N, направленной перпендикулярно к направлению движения точки, равна нулю:
AN = Nl cos 90° = 0;
работа силы F
AF = Fl cos 180° = -Fl = -fGl cos α,
так как сила трения
F = fN = fG cos α.
Подставим в выражение (а) полученные значения работ:
AP = -(AG + AN + AF) = Gl sin α + fGl cos α.
Таким образом,
A = AP = Gl(sin α + f cos α) = 50*4*(sin 20° + 0,2 cos 20°) = 106 кГ*м.
5. К. п. д. наклонной плоскости найдем так же, как в п. 5 первого решения.
🎥 Видео
Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

ЕГЭ. Физика. Силы трения. Наклонная плоскость. ПрактикаСкачать

подвижный клин наклонная плоскостьСкачать

Применение II закона Ньютона. Разбор на примерахСкачать

Скольжение бруска по движущемуся клину | Физика ЕГЭ, динамика | 10, 11 классСкачать

#9 НАКЛОННАЯ плоскость. Сила ТРЕНИЯСкачать

Физика ЕГЭ 2022 Демидова (ФИПИ) 30 типовых вариантов, вариант 23, разбор заданий 1 - 23 (часть 1)Скачать

Почему вес тела на полюсе и на экваторе отличается? ФИЗИКА ЕГЭСкачать

Движение тела по вертикали под действием силы тяжести 6-30Скачать

Физика 2024. Пилим наклонную плоскость. Часть 3. КинематикаСкачать

доска и брусокСкачать

ВЕС ТЕЛА, измерение массы тел взвешиванием. Вес тела, движущегося с ускорениемСкачать

#51. Оптимизация функции времени в задаче на движение!Скачать

Неравномерное движение по окружности в вертикальной плоскостиСкачать
9 класс. повторение (силы) решение задачСкачать