Тело массой 1 кг движется так что пройденное расстояние от времени дается уравнением

Тело массой m = 0,5 кг движется так, что зависимость пройденного телом пути s от времени t дается уравнением s = A sin ωt, где А = 5 см и ω = π рад/с. Найти силу F, действующую на тело через время t = (l/6) c после начала движения.

Дано:

А = 5 см = 5·10 -2 м

Решение:

По второму закону Ньютона

Ускорение – это вторая производная от вектора перемещения s по времени

Сила будет равна

Ответ:

Видео:Урок 87. Движение по наклонной плоскости (ч.1)Скачать

Методические указания к решению задач и выполнению контрольных работ (стр. 2 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3

Видео:ДВИЖЕНИЕ ПО НАКЛОННОЙ ПЛОСКОСТИ | механика 10 классСкачать

2.20. Маховик, бывший неподвижным, начал вращаться равноускоренно и, сделав 40 полных оборотов, приобрёл угловую скорость 10 . Определить угловое ускорение маховика и продолжительность равноускоренного вращения.

Видео:Урок 37. Движение тела, брошенного под углом к горизонту (начало)Скачать

2.21. Тело массой m =1кг движется так, что пройденное расстояние от времени дается уравнением , где a =5см, . Найти ускорение, силу и импульс тела через с после начала движения.

2.22. Тело массой m =1кг движется так, что его коорди — наты х и у изменяются от времени следующим образом: , , где , . Опреде — лить ускорение и действующую на тело силу к концу пятой секунды.

2.23. Определить ускорение грузов массы , , в системе. Массой блоков пренебречь. Трение отсутствует.

2.24. Шар массой m, двигаясь со скоростью υ, упруго ударяется о гладкую неподвижную стенку так, что скорость направлена под углом a к нормали. Определить импульс, получаемый стенкой.

2.25. В установке, показанной на рисунке, массы тел равны m1, m2 и m3 , масса блока пренебрежимо мала и трения в блоке нет. Найти ускорение, с которым опускается тело m3, и силу натяжения нити, связываю — щей тела m1 и m2, если коэффициент трения между этими телами и горизонтальной поверхностью равен k.

2.26. В системе, показанной на рисун — ке, массы тел равны m0, m1 , m2 , трения нет, массы блоков пренебрежимо малы. Найти ускорение тела m1.

2.27. Через невесомый блок, укреплен — ный на краю стола, перекинута нерастяжи — мая нить, связывающая грузы с массами m1 =1 кг и m2 =2 кг. Стол движется вверх с ускорением а0 =1 м/с. Найти ускорение груза m1 относительно стола и относительно земли. Трением пренебречь.

2.28. С каким минимальным ускоре — нием следует перемещать в горизонталь — ном направлении брусок А, чтобы тела 1 и 2 не двигались относительно него? Массы тел одинаковы, коэффициент трения между бруском и обоими телами равен k. Массой блока пренебречь.

2.29. Определить ускорение грузов массы , и , а также силу натяжения нитей в

системе блоков, если . Массой блоков пренебречь. Трение отсутствует.

2.30. Невесомая нерастяжимая нить, перекинутая через неподвижный блок, пропу — щена через щель. При движении нити на неё со стороны щели действует постоянная сила трения . На концах нити подвешены грузы m1 и m2. Определить ускорение грузов.

2.31. Шар, движущийся со скоростью 2 м/с, ударяется центрально в неподвижный шар такой же массы. Определить скорости шаров после удара в случае, если удар упругий и если удар неупругий.

2.32. Охотник стреляет вдоль лодки под углом 60º к горизонту. Какую скорость имел при вылете заряд ружья, если его масса 50 г. и если лодка приобрела скорость 0,05 м/с? Масса лодки и охотника 180 кг.

2.33. Мяч, летящий со скоростью υ0 = 15м/с, отбрасы — вается ракеткой в противоположную сторону со скоростью υ1=20м/с. Найти изменения импульса, если изменение кинети — ческой энергии ΔW = 8,75 Дж.

2.34. Два шара массой m1 = 9 кг и m2 = 12 кг подвешены на нитях длиной l = 1,5 м. Первоначально шары соприкасают —

ся между собой, затем меньший шар отклонили на угол α = 30º и отпустили. Считая удар неупругим, определить высоту h, на которую поднимутся оба шара после удара.

2.35. Два шара подвешены на параллельных нитях одинаковой длины так, что они соприкасаются. Масса первого шара 0,2 кг, масса второго – 0,1 кг. Первый шар отклоняют так, что его центр тяжести поднимается на высоту 4,5 см, и отпускают. На какую высоту поднимутся шары после соударения, если: а) удар упругий, б) удар неупругий?

2.36. Шар массой m1= 6 кг движется со скоростью υ1 =2 м/с и сталкивается с шаром массой m2 = 4 кг, который движется ему навстречу со скоростью υ2 = 5 м/с. Найти скорость шаров после прямого центрального удара. Удар считать абсолютно упругим.

2.37. Шар массой m1=5кг движется со скоростью υ1 = =2 м/с и сталкивается с покоящимся шаром массой m2 =3 кг. Вычислить работу, совершенную при деформации шаров при прямом центральном ударе. Удар считать неупругим.

2.38. На покоящийся шар налетает со скоростью υ = =4 м/с другой шар одинаковой с ним массы. В результате столкновения шар изменил направление движения на угол 30°. Определить скорости шаров после удара. Удар считать упругим.

2.39. На железнодорожной платформе, движущейся по инерции со скоростью υ0 = 3 км/ч, укреплено орудие. Масса платформы с орудием М = 10 т. Ствол орудия направлен в сторону движения платформы. Снаряд массой m=10 кг вылета — ет из ствола под углом α = 60­º к горизонту. Определить скорость снаряда (относительно Земли), если после выстрела скорость платформы уменьшилась в n = 2 раза.

2.40. Частица массы m1 налетела со скоростью υ на неподвижную частицу массы m2, которая после упругого уда — ра полетела под углом α к первоначальному направлению движения налетающей частицы. Определите скорость частицы m2 после удара.

2.41. Подсчитать работу поднятия груза массой m= =200кг по наклонной плоскости длиной l = 5 м, составляю — щей с горизонтом угол α = 30º, если ускорение тела при подъёме равно а = 0,5 м/с2, коэффициент трения μ = 0,1.

2.42. Вагон массой m = 20 т, двигаясь равнозамедленно с начальной скоростью υ0=54 км/ч, останавливается через некоторое время под действием силы трения, которая изменя — ется с расстоянием по закону F=–a x, где a =100н/м. Найти работу силы трения и расстояние, которое пройдёт вагон до остановки.

2.43. На какую глубину погрузится тело, падая с высоты h в воду, если плотность тела ρ меньше плотности воды ρ1? Трением тела о воздух и воду пренебречь.

2.44. Сила, действующая на частицу, имеет вид , где а – константа. Вычислить работу, совершаемую над частицей этой силой на пути от точки с координатами (1,2,3) м до точки с координатами (7,8,9) м.

2.45. Тело массой m начинает двигаться под действием силы . Найти мощность, развиваемую силой в момент времени t.

2.46. Тело массой m = 1,0 кг падает с высоты h=20м. Пренебрегая сопротивлением воздуха, найти среднюю по времени мощность, развиваемую силой тяжести на пути h, и мгновенную мощность на высоте h/2.

2.47. Спортсмен с высоты h = 12 м падает на упругую сетку. Пренебрегая массой сетки, определить, во сколько раз наибольшая сила давления спортсмена на сетку больше его силы тяжести, если прогиб сетки под действием только силы тяжести спортсмена х0 = 15 см.

2.48. Пуля массой m = 15г, летящая горизонтально, попадает в баллистический маятник длиной l = 1 м и массой М = 1,5 кг и застревает в нём. Маятник в результате этого отклонился на угол φ = 30º. Определить скорость пули.

2.49. Потенциальная энергия частицы имеет вид U = а/r, где r – модуль радиус-вектора частицы, а= const. Найти силу , действующую на частицу, работу, совершаемую этой силой над частицами при её переходе из точки М(1,2,3) в точку N(2,3,4).

2.50. Конькобежец, стоя на льду, бросил вперёд гирю массой m1=5кг и вследствие отдачи покатился назад со скоро — стью υ2=1м/с. Масса конькобежца m2=60кг. Определить работу А, совершённую конькобежцем при бросании гири.

2.51. На барабан, представляющий однородный цилиндр радиусом R = 0,2 м и массой m1 = 9 кг, намотан шнур, к концу которого привязан груз массой m2 = 2 кг. Найти ускорение груза и кинетическую энергию системы, спустя время t =3 с.

2.52. В установке, показанной на рисунке, известны масса однородного сплошного цилиндра m, его радиус R и массы тел m1 и m2. Найти угловое ускорение цилиндра и отношение сил натяжений Т2/Т1 вертикальных участков нити в процессе движения.

2.53. В системе, показанной на рисунке, известны массы тел m1 и m2 , коэффициент трения k между телом m1 и горизонтальной плоскостью, а также мас — са блока m, который можно считать однородным диском. Найти ускорение тела m2 и работу силы трения, дейст — вующей на тело m1, за первые t секунд после начала движения.

2.54.Однородный цилиндр массой m и радиусом R начинает опускаться под действием силы тяжести. Найти угловое ускорение цилиндра и натяжение каждой нити.

2.55. На стержень радиусом r наглухо насажен сплошной диск радиусом R и массой m. К стержню прикреплены нити, при помощи которых диск подвешивается к штативу. Найти ускорение, с которым опускается диск. Массой стержня пренебречь.

2.56. Найти ускорение центра однородного шара, скатывающегося без скольжения по наклонной плоскости, образующей угол a с горизонтом. Чему равна сила трения между шаром и плоскостью?

2.57. Определить линейную скорость центра шара, скатив — шегося без скольжения с наклонной плоскости высотой h=1 м.

2.58. На барабан радиусом R=0,5м намотан шнур, к кото — рому привязан груз массой m = 10 кг. Найти момент инерции барабана J, если известно, что груз опускается с ускорением а = 2,04 м/с2.

2.59. На барабан радиусом R=20см, момент инерции которого J=0,1 кг∙м2, намотан шнур, к концу которого привязан груз массой m=0,5кг. До начала вращения барабана груз находился на высоте h =1 м над полом. Через какое время груз опустится на пол и какова будет при этом кинетическая энергия системы?

2.60. Маховик в виде сплошного диска, момент инерции которого J=1,5 кг∙м2, вращаясь при торможении равнозамед — ленно, за время t=1 мин уменьшил частоту своего вращения с n0 = 240 об/мин до n1 = 120 об/мин. Определить: 1) угловое ускорение маховика; 2) момент силы торможения; 3) работу торможения.

2.61. На скамье Жуковского сидит человек и держит в вытянутых руках гири по 10 кг каждая. Расстояние от каждой гири до оси вращения скамьи l1=50 см. Скамья вращается с частотой n1=1 с–1. Как изменится частота вращения скамьи и какую работу произведет человек, если он сожмет руки так, что расстояние от каждой гири до оси уменьшится до l2=20см? Суммарный момент инерции человека и скамьи относительно оси вращения J = 2,5 кг м2.

2.62. На краю свободно вращающегося достаточно большого горизонтального диска, имеющего радиус R и момент инерции J, стоит человек массой m. Диск совершает n1 об/мин. Как изменится угловая скорость вращения диска, если человек перейдет от края диска к центру? Какую работу совер — шит человек при переходе? Размерами человека по сравнению с радиусом диска можно пренебречь.

2.63. Шарик массой m =50 г, привязанный к концу нити длиной l1=1 м, вращается с частотой n1=1 об/с, опираясь на горизонтальную плоскость. Нить укорачивается, приближая шарик к оси вращения до расстояния l2=0,5 м. С какой часто — той будет при этом вращаться шарик? Какую работу совершает внешняя сила, укорачивая нить? Трением шарика о плоскость пренебречь.

2.64. На краю горизонтальной платформы, имеющей форму диска радиусом R=2 м, стоит человек. Масса платформы M=240 кг, масса человека m=80 кг. Платформа может вращать — ся вокруг вертикальной оси, проходящей через ее центр. Пренебрегая трением, найти с какой угловой скоростью будет вращаться платформа, если человек будет идти вдоль ее края со скоростью υ = 2 м/с относительно платформы.

2.65. Человек стоит на скамье Жуковского и держит в руках стержень, расположенный вертикально вдоль оси вращения скамейки; стержень служит осью вращения колеса, расположенного на верхнем конце стержня. Скамья неподви — жна, колесо вращается с частотой n1=10 с–1. Радиус колеса равен 20см, его масса m =3 кг. Определить частоту вращения n2 скамьи, если человек повернет стержень на угол 180°? Суммарный момент инерции человека и скамьи равен 6 кг×м2.

2.66. Вертикально расположенный однородный стержень массы M и длины l может вращаться вокруг своего верхнего конца. В нижний конец стержня попала, застряв, горизонталь — но летевшая пуля массы m, в результате чего стержень отклонился на угол a. Считая m ,

где = m0 2/2 — средняя кинетическая энергия поступательного движения молекулы газа; n — число молекул газа в единице объема.

6. Cредняя кинетическая энергия молекулы газа:

где i — число степеней свободы молекулы.

7. Скорость молекул:

— средняя квадратичная скорость поступательного движения молекул

;

;

,

где m — масса одной молекулы, М – масса моля.

8. Распределение молекул газа по скоростям (распределение Максвелла):

где dn — число молекул идеального газа из общего числа n, имеющих при температуре Т скорости в интервале υ, υ + dυ.

9. Распределение частиц в силовом поле (распределение Больцмана):

где U — потенциальная энергия частиц; n0 – концентрация молекул на нулевом уровне.

10. Среднее число соударений, испытываемых одной молекулой газа в единицу времени:

,

где d — эффективный диаметр молекулы; n — концентрация молекул; — средняя арифметическая скорость молекул.

11. Средняя длина свободного пробега молекул газа:

.

12. Закон Фика (уравнение диффузии):

где Dm — масса газа, перенесенная в результате диффузии через площадку S за время Dt; D =(1/3) — коэффициент диффузии; dr/dx — градиент плотности в направлении, перпендикулярном к площадке.

13. Закон Фурье (уравнение теплопроводности):

где DQ — количество теплоты, перенесенное газом в результате теплопроводности через площадку S за время Dt; dT/dx — градиент температуры в направлении, перпендикулярном к площадке S; K = (1/3) cvr — коэффициент диффузии. Здесь cv — удельная теплоемкость газа при постоянном объеме; r — плотность газа.

14. Сила внутреннего трения между движущимися слоями газа:

где h=(1/3)r — коэффициент вязкости; dυ/dx— градиент скорости в направлении, перпендикулярном к площадке S.

15. Первое начало термодинамики:

где dQ — количество теплоты, сообщенное системе; dА = p dV — элементарная работа, совершенная системой против внешних сил; dU = m/M cv dT — изменение внутренней энергии.

16. Теплоемкость идеального газа:

Молярные теплоемкости при постоянном объеме и постоян — ном давлении

где i — число степеней свободы молекул газа.

17. Уравнение Пуассона:

где g = Ср/Сv = (i+2)/i — коэффициент Пуассона.

18. Работа, совершаемая газом:

а) в общем случае А = ò рdV;

б) при изобарном процессе (р= const) A= p (V2 ‑ V1);

в) при изотермическом процессе (Т=const)

г) при адиабатном процессе (dQ = 0)

19. К. п.д. тепловой машины:

где Q1 — тепло, получаемое рабочим телом, Q2¢ — отдаваемое тепло.

К. п.д. цикла Карно:

где Т1 и Т2 — температуры нагревателя и холодильника.

20. Приращение энтропии системы:

где dQ — элементарное тепло, получаемое системой.

21. Связь между энтропией и термодинамической вероятностью:

где k — постоянная Больцмана, W — термодинамическая вероятность системы.

3.2. Примеры решения задач

Задача 1. В сосуде объёмом V = 5 л находится азот массой m = 1,4 г при температуре Т = 1800 К. Найти давление газа, имея в виду, что при этой температуре h =30% молекул диссоциировано на атомы.

Видео:Тело массой 1 кг движется по горизонтальной плоскости. На тело действует силаСкачать

Решение

Так как часть молекул диссоциирована на атомы, то в сосуде находится смесь двух газов с молярными массами М1=28 г и М2 = М1/2 =14 г уравнения состояния обоих газов имеют вид:

(1)

(2)

где P1 и P2 – парциальные давления молекулярного (N2) и атомарного (N1) азота. Давление смеси газов подчиняется закону Дальтона:

Сложим уравнения (1) и (2):

Так как m1+m2=m (масса газа), то

Задача 2. На какой высоте давление воздуха составляет 60 % от давления на уровне моря? Считать температуру воздуха везде одинаковой и равной 10О С.

Зависимость давления от высоты имеет вид:

На уровне моря h0=0, поэтому

Прологарифмируем обе части

Задача 3. Найти среднюю продолжительность свобод — ного пробега молекул кислорода при температуре Т = 250 К и давлении P =100 Па.

Видео:Урок 18 (осн). Координаты тела. График движения. График скоростиСкачать

Решение

Средняя продолжительность свободного пробега молекул – величина, обратная среднему числу столкновений, происходящих за 1 секунду:

Так как то

.

Здесь — средняя арифметическая скорость молекул кислорода

где n – концентрация молекул кислорода.

Из уравнения состояния идеального газа

Эффективный диаметр молекул кислорода (величина справочная) d = 0,36 нм = .

Задача 4. Определить отношение удельных теплоём — костей g для смеси газов, содержащей гелий массой m1=8 г и водород массой m2 = 2 г.

Видео:Урок 16 (осн) Средняя скорость. Вычисление пути и времени движенияСкачать

Решение

Для нагревания смеси газов массой на DT при постоянном объёме ей необходимо сообщить количество теплоты где — удельная теплоёмкость смеси.

Часть этого количества теплоты, пойдёт на нагревание гелия, другая часть — на нагревание водорода. Тогда

,

.

Аналогично находим ср смеси:

.

Здесь , и ,— удельные теплоёмкости гелия и водорода соответственно:

Так как гелий – газ одноатомный, то i1=3, водород – газ двухатомный, следовательно, i2=5.

Отношение удельных теплоёмкостей:

Подставляя выражение для удельных теплоёмкостей, получим:

.

Задача 5. Идеальный газ с g =1,4 расширяется изотерми — чески от объёма V1 = 0,1 м3 до объёма V2 = 0,3 м3. Конечное давление газа Па. Определить приращение внутрен- ней энергии газа, совершённую газом работу и количество теплоты, полученное газом.

Видео:Урок 128. Соударения телСкачать

Решение

Так как температура газа не изменится, то приращение его внутренней энергии DU=0. Тогда I начало термодинамики запишется в виде:

Работа при изотермическом процессе

Значение vRT найдём из уравнения состояния идеального газа

Тогда .

Задача 6. При адиабатном расширении (v = 2 моль) кислорода, находящегося при нормальных условиях, его объём увеличился в n = 3 раза. Определить изменение внутренней энергии газа и работу расширения газа.

Решение

Первый закон термодинамики для адиабатного процесса имеет вид:

Изменение внутренней энергии газа

.

Конечную температуру найдём из уравнения адиабаты:

; .

Так как и газ двухатомный, то

.

Тогда .

.

Задача 7. Вычислить К. П.Д. цикла, состоящего из изобарного, адиабатного и изотермического процессов, если в результате изобарного процесса газ нагревается от Т1=300 К до Т2=600 К.

В процессе изобар — ного нагревания 1-2 газ расширяется за счёт поступившего от нагрева — теля количества тепла Q12, в процессе адиабатного расширения 2-3 dQ=0, в процессе изотермического сжатия газ отдаёт количе — ство теплоты Q31 холодиль — нику. К. п.д. любого цикла определяется выражением

,

.

Первый закон термодинамики для процесса 3-1 имеет вид:

.

Так как работа при изотермическом процессе равна

, то . Объём газа в состоянии 1 найдём из уравнения изобары ; .

Видео:Графики зависимости пути и скорости от времениСкачать

Тело массой m = 1кг движется так, что его координаты x и y изменяются от времени следующим образом : x = a — bt + ct ^ 2, y = dt ^ 3, где c = 1 м / с ^ 2, d = 2 м / с ^ 2?

Физика | 10 — 11 классы

Тело массой m = 1кг движется так, что его координаты x и y изменяются от времени следующим образом : x = a — bt + ct ^ 2, y = dt ^ 3, где c = 1 м / с ^ 2, d = 2 м / с ^ 2.

Определить ускорение и действующую на тело силу к концу пятой секунды.

Ax(t) = x»(t) = 2 * c = 2 м / с2

ay(t) = y»(t) = 6 * d * t

a(5) = 6 * 2 * 5 = 60 м / с2

a = sqrt(ax ^ 2 + ay ^ 2) = sqrt(4 * 2 + 60 ^ 2) = 60, 03 м / с2

F = m * a = 1 * 60, 03 = 60, 03 H.

Видео:Урок 40. Задачи на движение тела, брошенного под углом к горизонту (ч.1)Скачать

Найти силу действующую на тело массой 500кг если тело движется прямолинейно и его координата изменяется по закону х = 20 — 10t + t²?

Найти силу действующую на тело массой 500кг если тело движется прямолинейно и его координата изменяется по закону х = 20 — 10t + t².

Видео:Взаимодействие тел. Масса тела. Единицы массы | Физика 7 класс #14 | ИнфоурокСкачать

Тело массой 2кг движется с ускорением, изменяющимся по закону а = 5t — 10 определить силу, действующую на тело через 5 с после начала действия, и скорость в конце пятой секунды?

Тело массой 2кг движется с ускорением, изменяющимся по закону а = 5t — 10 определить силу, действующую на тело через 5 с после начала действия, и скорость в конце пятой секунды.

Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Тело массой 3кг движется с ускорением 1?

Тело массой 3кг движется с ускорением 1.

Определите силу , действующую на тело.

Видео:Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Тело массой 200 г движется с ускорением 2м / с в квадрате?

Тело массой 200 г движется с ускорением 2м / с в квадрате.

Определить силу действующую на тело.

Видео:Шаговое напряжение.Как это работает и как безопасно от него уйтиСкачать

Тело массой 2500 кг движется с у ускорением 0, 2 м / с в квадрате?

Тело массой 2500 кг движется с у ускорением 0, 2 м / с в квадрате.

Определите силу действующую на тело.

Видео:Урок 62. Сила тяжести и вес тела. Невесомость.Скачать

Под действием силы 10Н тело движется с ускорением 5 метров секунду квадрате Какова масса тела?

Под действием силы 10Н тело движется с ускорением 5 метров секунду квадрате Какова масса тела.

Видео:Физика - движение тела, брошенного под углом к горизонтуСкачать

Под действием силы 4 H тело движется с ускорением 2м / с²?

Под действием силы 4 H тело движется с ускорением 2м / с².

Определить массу тела.

Видео:Задача на теорему о движении центра массСкачать

С каким ускорением движется тело массой 300 г под действием силы 0?

С каким ускорением движется тело массой 300 г под действием силы 0.

Определитескорость тела в конце десятой секунды движения.

Оцените сколько времени так может двигаться тело в земных условиях.

Видео:Определите силу, действующую на тело массой 1 кг, находящееся на расстоянии 600 км от поверхности...Скачать

Определить ускорение, с которым движется тело массой 500г под действием силы 6H?

Определить ускорение, с которым движется тело массой 500г под действием силы 6H.

Видео:Физика - движение по окружностиСкачать

Тело массой 2 кг движется с ускорением, изменяющемся по закону a = 5t — 10?

Тело массой 2 кг движется с ускорением, изменяющемся по закону a = 5t — 10.

Определите силу, действующую на тело через 5с после начала действия, и скорость в конце пятой секунды.

На странице вопроса Тело массой m = 1кг движется так, что его координаты x и y изменяются от времени следующим образом : x = a — bt + ct ^ 2, y = dt ^ 3, где c = 1 м / с ^ 2, d = 2 м / с ^ 2? из категории Физика вы найдете ответ для уровня учащихся 10 — 11 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.

Видео:ЕГЭ по математике. Профильный уровень. Задание 7. Закон движения. ПроизводнаяСкачать

ДИНАМИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ. 60. Тело массой 1 кг движется так, что зависимость его скорости от времени движения задано уравнением: V = А sinwt (А=5 см

60. Тело массой 1 кг движется так, что зависимость его скорости от времени движения задано уравнением: V = А sinwt (А=5 см, w=p рад/с). Определить силу, действующую на тело через 1/6 c после начала движения. Какой путь пройдет тело к этому моменту времени? (0,14 Н, 1,4 см).

61. Автомобиль массой 1000 кг останавливается при торможении за 5 секунд, пройдя при этом равнозамедленно расстояние 25 метров. Найти начальную скорость автомобиля и силу торможения. (10 м/с; 2 кН).

62. Тело массой 2 кг двигается под действием некоторой силы по закону

(координата Х измеряется в метрах, время t — в секундах). Определить момент времени, в который сила, действующая на тело, равна нулю. Чему равен импульс тела в этот момент? (1,67с, 13,3 кг м/с).

63. На тело массой 1 кг, лежащее на горизонтальной поверхности, начинает действовать сила 100 Н, направленная вверх под углом 30° к горизонту. Какой путь пройдет тело по горизонтальной поверхности за 1 секунду? Коэффициент трения тела о поверхность равен 0,1. (45,3 м).

64. Груз массой 30 кг придавливается к вертикальной стене горизонтальной силой F₁ =100 Н. Чему должна быть равна сила F₂, направленная вертикально вверх, чтобы груз двигался по стене вертикально вверх равномерно? Коэффициент трения груза о стену равен 0,2. (314 Н)

65. К потолку трамвайного вагона подвешен на нити шар. Вагон начинает двигаться равнозамедленно и за 3 секунды его скорость уменьшается от 18 до 6 км/ч. На какой угол отклонится при этом нить с шаром? (6° 30 ¢ )

66. Шарик массой 1 кг прикреплен двумя одинаковыми нитями к доске, которая поднимается вертикально вверх с ускорением а = 0,2 м/с 2 . Определить натяжение каждой нити, если угол a между ними составляет 60°. (5,8 Н).

67. Тело скользит по наклонной плоскости, угол наклона которой к горизонту составляет 30°. Коэффициент трения между телом и плоскостью равен 0,1. Найти ускорение тела. (4,1 м/с 2 ).

68. Тело находится на наклонной плоскости. При каком предельном угле наклона плоскости к горизонту тело не будет скользить по ней? Коэффициент трения тела о плоскость 0,1. (5,7°).

69. Тело массой 5 кг лежит на полу лифта, опускающегося вниз с ускорением 2 м/с 2 . Определить вес тела. Как и с каким ускорением должен двигаться лифт, чтобы вес тела был равен 49 Н? 59 Н? (39 Н,.0.м/с 2 , 2.м/с 2 ).

70. К потолку лифта массой 300 кг подвешен груз массой 50 кг. Под действием силы 4 кН лифт поднимается вверх. Найти вес груза. (571 Н).

71. Наклонная плоскость, образующая угол 25° с плоскостью горизонта, имеет длину 2 м. Тело, двигаясь равноускоренно, соскользнуло с этой плоскости за 2 секунды. Определить коэффициент трения тела о плоскость. (0,35)

72. Вагонетка начинает двигаться вниз по наклонной плоскости, составляющей с горизонтом угол 30°. Определить скорость вагонетки через 5 с после начала движения, если коэффициент трения равен 0,5. (3,3 м/с).

73. На тело массой 1 кг, двигающееся по наклонной плоскости, действует горизонтально направленная сила F = 10 Н. Определить силу, с которой тело давит на плоскость и его ускорение, если угол a = 30 0 , а коэффициент трения тела о плоскость 0,1.(3,6 Н, 13,2 м/с 2 ).

74. Тело массой 10 кг движется по наклонной плоскости вверх с постоянным ускорением. На тело действует сила 100 Н, направленная вверх под углом 30° к поверхности наклонной плоскости. Коэффициент трения 0,1, угол наклона плоскости к горизонту 30°. Определить ускорение тела. (3,3 м/с 2 ) .

75. В установке углы a и b равны соответственно 30° и 45°, массы тел m₁ =0,45 кг и m₂ =0,5 кг. Считая нить и блок невесомыми и пренебрегая силами трения, определить ускорение, с которым движутся тела, и силу натяжения нити. (0,7 м/с 2 , 2,8 Н).

76. В установке угол a наклонной плоскости с горизонтом равен 20°, массы тел m₁ =200 г и m₂ =150 г. Считая нить и блок невесомыми и пренебрегая силами трения, определить ускорение, с которым будут двигаться тела. Тело m₂ опускается. (2,3 м/с 2 ).

77. Парашютист массой 80 кг совершает затяжной прыжок. Считая, что сила сопротивления воздуха пропорциональна скорости, определить, через какой промежуток времени скорость движения парашютиста будет равна 0,9 от максимальной (скорости установившегося движения). Начальная скорость равна нулю, коэффициент сопротивления движению составляет 10 кг/с. (18,4 с).

78. Грузы одинаковой массы m=0,5 кг соединены невесомой нитью и перекинуты через невесомый блок, укрепленный на конце стола. Коэффициент трения груза о стол равен 0,15. Пренебрегая трением в блоке, определить ускорение, с которым движутся грузы, и силу натяжения нити. (4,17 м/с 2 ; 2,82 Н).

79. Чтобы определить коэффициент трения между деревянными поверхностями, брусок положили на доску и стали поднимать один конец доски до тех пор, пока брусок не начал по ней скользить. Это произошло при угле наклона доски 14°. Чему равен коэффициент трения? (0,25).

80. На горизонтальном столе лежат два тела одинаковой массы m₁=m₂=1 кг, связанные невесомой нерастяжимой нитью. Такая же нить перекинута через невесомый блок и связывает второе тело с грузом массы m₃=0,5 кг. Коэффициент трения первого тела о стол составляет 0,10, второго — 0,15. Определить ускорение, с которым движутся тела, и натяжение нити, на которой висит груз. (0,98 м/с 2 ; 4,4 Н).

81. Два соприкасающихся бруска массами m₁ =3 кг и m₂ =2 кг скользят по наклонной доске, составляющей с горизонтом угол 45°. Коэффициенты трения между брусками и доской соответственно равны k₁ = 0,2 и k₂ = 0,1. Определить ускорение, с которыми движутся бруски и силу, с которой они давят друг на друга. (5,8 м/с 2 ; 0,8 Н).

82. Два груза массами m₁ =500 г и m₂ =700 г связаны невесомой нерастяжимой нитью и лежат на гладком столе. К грузу m₁ приложена горизонтально направленная сила F, равная 6 Н. Пренебрегая трением, определить ускорение грузов и силу натяжения нити.(5 м/с 2 ; 3,5 Н).

83. Наклонная плоскость с углом наклона a = 30° к горизонту движется горизонтально с ускорением а. При каком значении ускорения тело, лежащее на наклонной плоскости, начнет подниматься по ней? Коэффициент трения между телом и плоскостью равен 0,1. (4,7 м/с 2 ).

84. Тело А массой 2 кг находится на горизонтальном столе и соединено посредством невесомых блоков с телами В (массой 0,5 кг) и С (массой 0,3 кг). Считая нити нерастяжимыми и невесомыми и пренебрегая силами трения, определить ускорение, с которым будут двигаться грузы и разность сил натяжения нитей. (0,78 м/с 2 ; 1.33 Н).

85. Снаряд массой 10 кг выпущен из зенитного орудия вертикально вверх со скоростью 800 м/с. Считая силу сопротивления воздуха пропорциональной скорости, определить время подъема снаряда до высшей точки траектории. Коэффициент сопротивления движению 0,25 кг/с. (44,5 с).

86. Радиус одного из астероидов, имеющего форму шара, 5 км, его плотность 5,5 г/см 3 . Определить:1) ускорение свободного падения на поверхности астероида; 2) высоту подъема тела, брошенного вертикально вверх от поверхности астероида с такой же скоростью, с какой нужно бросить вертикально вверх тело на Земле для подъема на высоту 4,9 см. (0,008 м/с 2 , 60 м).

87. Через невесомый блок, укрепленный в вершине наклонной плоскости, перекинута веревка с двумя грузами одинаковой массы m = 1 кг Коэффициент трения между наклонной плоскостью и лежащим на ней грузом равен 0,1, угол a наклона плоскости к горизонту составляет 30°. Пренебрегая трением в блоке, найти силу натяжения нити. (7,8 Н).

88. Тело скользит по наклонной плоскости, составляющей с горизонтом угол 8°, а потом по горизонтальной поверхности. Определить коэффициент трения (считая его постоянным), если известно, что тело по горизонтали проходит такое же расстояние, как и по наклонной плоскости. (0,07).

89. К концам нерастяжимой невесомой нити, перекинутой через блок, подвешены два одинаковых свинцовых шарика. Правый шарик опущен в сосуд с глицерином. Определить ускорение, с которым движутся шарики. (0,52 м/с 2 ).

90. К концам нити, перекинутой через блок, подвешены два груза: слева 50 г и справа 100 г. Через какое время правый груз опустится на 50 см? (0,55 с).

91. Найти силу тяги, развиваемую мотором автомобиля, движущегося по горизонтальному пути с ускорением 1 м/с 2 . Масса автомобиля 1000 кг, коэффициент трения 0,1. (1980 Н).

92. На столе лежит цепочка, свешивающаяся наполовину за край стола. С каким ускорением начнет соскальзывать цепочка, если коэффициент трения ее о поверхность стола равен 0,3? (3,4 м/с 2 ).

93. Груз массой 5 кг поднят при помощи каната вертикально вверх в течение 2 с на высоту 10 м. Считая движение груза равноускоренным, определить силу натяжения каната. (74 Н).

94. Буксирный теплоход тянет равноускоренно две баржи водоизмещением 500 т и 300 т. Сила сопротивления воды для первой баржи равна 15 кН, для второй 12 кН. Найти натяжение троса между баржами, если сила тяги буксира 50 кН. (20,6 кН).

95. К телу массой 1 кг приложены две взаимно перпендикулярные силы по 10 Н каждая. Определить расстояние, пройденное телом через 1 с после начала движения. (7 м).

96. Сани массой 5 кг скатываются с ледяной горки с ускорением 4 м/с 2 . Какую силу параллельную склону необходимо приложить, чтобы втаскивать санки в гору равномерно. Уклон горы 30°. (29,2 Н).

97. По наклонной плоскости с высоты 0,5 м скользит тело. Пройдя 1 м, тело приходит к основанию наклонной плоскости со скоростью 2,45 м/с. Определить коэффициент трения тела о плоскость.(0,22)

98. Космическая ракета летит на Луну. В какой точке прямой, соединяющей центры Луны и Земли, ракета будет притягиваться Землей и Луной с одинаковой силой? (3,4´10 5 км от поверхности Земли).

99. Вагон под действием силы тяжести катится вдоль дороги, составляющей угол 30° с горизонтом. Сила трения составляет 10% от веса вагона. К потолку вагона на нити подвешен шарик массой 15 г. Определить силу натяжения нити и угол ее отклонения от вертикали. (0,15 Н, 23°).

ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ.

100. Вал в виде сплошного цилиндра массой 10 кг насажен на горизонтальную ось. На цилиндр намотан шнур, к свободному концу которого подвешена гиря массой 2 кг. С каким ускорением будет опускаться гиря? (2,8 м/с 2 ).

101. Найти вес автомобиля массой 2 тонны, движущегося со скоростью 36 км/ч по выпуклому мосту радиусом 100 м. (17600 Н).

102. Через блок в виде сплошного диска, имеющего массу 80 г, перекинута невесомая нерастяжимая нить, к концам которой подвешены грузы массами 100 г и 200 г. С каким ускорением будут двигаться грузы, если их предоставить самим себе? Трением пренебречь. (2,9 м/с 2 ).

103. Маховик в виде сплошного диска радиусом 0,2 м и массой 50 кг раскручен до частоты вращения 480 об/мин. и предоставлен самому себе. Под действием сил трения маховик остановился через 50 с. Найти момент сил трения, считая его постоянным. (1 Н´м).

104. Шар массой 0,2 кг и радиусом 2 см вращается вокруг оси, проходящей через его центр масс. Угол поворота изменяется по закону j = 5t 5 + 3t + 14 (угол j — в радианах, время t — в cекундах). Найти результирующий момент сил, действующий на тело в момент времени 10 с. (3,2 Н´м).

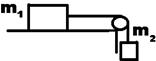105. На горизонтальном столе лежит тело массой m₁ =2 кг, которое может скользить по столу без трения. Оно связано невесомой, нерастяжимой нитью, перекинутой через блок, с грузом массой m₂ = 0,5 кг. Блок — сплошной однородный цилиндр массой 1 кг. Считая, что блок вращается без трения, а нить не проскальзывает по блоку, найти ускорение тел. (1,6 м/с 2 ).

106. Найти угловое ускорение блока в условиях предыдущей задачи, если радиус блока 10 см, а коэффициент трения тела о стол k = 0,1.(9,8 с -2 ).

107. Маховик, момент инерции которого равен 63,6 кг м 2 , вращается с постоянной угловой скоростью 3,14 рад/с. Найти тормозящий момент, cчитая его постоянным, под действием которого маховик останавливается через 20 с. (10 Н´м).

108. Маховик в виде диска радиусом 0,2 м и массой 10 кг соединен с мотором при помощи приводного ремня. Натяжение ремня, идущего без скольжения, постоянно и равно 14,7 Н. Какое число оборотов в секунду будет делать маховик через 10 с после начала движения? (23,4 об/с).

109. Маховик с моментом инерции 245 кг´м 2 вращается, делая 20 об/с. Через минуту после того, как на маховик перестал действовать вращающий момент, он остановился. Найти момент сил трения и число оборотов, которое сделал маховик до полной остановки после прекращения действия вращающего момента. (513 Н´м, 600 об.).

110. Блок массой 1 кг укреплен на конце стола (см. рис. к задаче 105). Тела одинаковой массы по 1 кг соединены невесомой и нерастяжимой нитью, перекинутой через блок. Коэффициент трения тела о стол 0,1. Найти ускорение, с которым движутся тела и силы натяжения нитей для каждого тела. Блок считать однородным диском. Трением в блоке пренебречь. (3,5 м/с 2 , 6,3 Н, 4,5 Н).

111. Маховик в виде диска массой 50 кг и радиусом 20 см был раскручен до угловой скорости 480 об/мин. и затем предоставлен самому себе. Под влиянием трения маховик остановился. Найти момент сил трения, если маховик до полной остановки сделал 200 оборотов (1 Н м).

112. На однородный сплошной цилиндрический вал радиусом 50 см намотана легкая нить, к концу которой прикреплен груз массой 6,4 кг. Груз, разматывая нить, опускается с ускорением 2 м/с 2 .Определить момент инерции вала и его массу. (6,25 кг´м 2 , 50 кг).

113. Маховик в виде диска радиусом 10 см был раскручен до угловой скорости 300 об/мин. и затем предоставлен самому себе. Под действием сил трения маховик остановился через 50 с. Найти массу диска, если момент сил трения равен 0,314 Н´м. (100 кг).

114. На однородный сплошной цилиндрический вал массой 40 кг намотана невесомая нить, к концу которой прикреплен груз массой 5 кг. Груз, разматывая нить, опускается с ускорением. Определить ускорение груза. (1,96 м/с 2 ).

115. На однородный сплошной цилиндрический вал массой 10 кг намотана невесомая нить, к концу которой прикреплен груз 1 кг. Определить зависимость пути от времени, согласно которой движется груз и силу натяжения нити. (S = 0,82 t 2 , 8,2 Н).

116. На однородный сплошной цилиндрический вал радиусом 20 см, момент инерции которого 0,15 кг´м 2 , намотана невесомая нить, к концу которой прикреплен груз массой 0,5 кг. До начала вращения вала высота груза над полом составляла 2,3 м. Определить время опускания груза до пола. (2 с).

117. Через блок в виде диска массой 0,2 кг перекинута невесомая нить, к концам которой прикреплены грузы массами 0,35 кг и 0,55 кг. Пренебрегая трением в оси блока, определить ускорение грузов и отношение сил натяжения нити по обе стороны блока. (1,96 м/с 2 , 1,05)

118. Тело массой 0,25 кг, соединенное невесомой нитью посредством блока в виде полого тонкостенного цилиндра с телом массой 0,2 кг, скользит по поверхности горизонтального стола. (См. рис. к задаче 105). Масса блока 0,15 кг, коэффициент трения тела о поверхность стола равен 0,2. Пренебрегая трением в оси блока, определить ускорение, с которым будут двигаться тела и силы натяжения нити по обе стороны блока. (2,45 м/с 2 , 1,1 Н, 1,47 Н).

119. Колесо, вращаясь равнозамедленно, уменьшило за 1 минуту частоту вращения от 300 об/мин. до 180 об/мин. Момент инерции колеса 2 кг м 2 . Найти угловое ускорение колеса, момент сил торможения и число оборотов, сделанных колесом за 1 минуту. (-0,21 рад/с 2 , 0,42 Н м, 240 оборотов)

120. Маховое колесо, момент инерции которого 245 кг´м 2 , вращается с частотой 20 об/с. После того, как на колесо перестал действовать вращающий момент, оно остановилось, сделав 1000 оборотов. Найти момент сил трения и время, прошедшее от момента прекращения действия вращающего момента до остановки колеса. (308 Н´м, 100 с).

121. По ободу шкива, имеющего общую ось с маховым колесом, намотана невесомая нить, к концу которой подвешен груз массой 1 кг. На какое расстояние должен опуститься груз, чтобы колесо со шкивом получило угловую скорость 60 об/мин.? Момент инерции колеса со шкивом 0,42 кг м 2 , радиус шкива 10 см. (0,865 м).

122. На шкив радиусом 0,1 м намотана невесомая нить, к свободному концу которой подвешен груз массой 2 кг. Груз опускается с ускорением 1 м/с 2 . Момент силы трения в оси шкива равен 1 Н´м. Определить момент инерции шкива. (7,6´10 -2 кг ´м 2 ).

123. Если к шкиву радиусом 0,5 м подвесить груз массой 2 кг, то он будет вращаться с угловым ускорением 2 рад/с 2 . Если груз снять, то шкив за счет силы трения будет вращаться равнозамедленно с угловым ускорением -1 рад/с 2 . Определить момент инерции шкива. (2,93 кг´м 2 ).

124. Определить момент силы, который необходимо приложить к блоку, вращающемуся с частотой 12 об/с, чтобы он остановился в течение 8 с. Диаметр блока 30 см. Масса блока распределена равномерно по ободу и равна 6 кг. (1,27 Н´м).

125. К ободу однородного сплошного диска радиусом 0,5 м приложена постоянная касательная сила 100 Н. При вращении диска на него действует момент сил трения 2 Н´м. Определить массу диска, если известно, что его угловое ускорение постоянно и равно 16 рад/с 2 . (24 кг).

🎦 Видео

Урок 85. Движение связанных тел (ч.1)Скачать