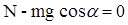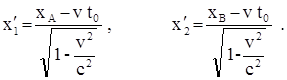Читайте также:
|
| Вариант | Номер задач |
101. Тело брошено вертикально вверх с начальной скоростью V0=4 м/с. Когда оно достигло верхней точки полета из того же начального пункта, с той же начальной скоростью V0 вертикально вверх брошено второе тело. На каком расстоянии h от начального пункта встретятся тела? Сопротивление воздуха не учитывать.
102. Материальная точка движется прямолинейно с ускорением а=5м/с 2 . Определить, на сколько путь, пройденный точкой в п-ю секунду, будет больше пути, пройденного в предыдущую секунду. Принять V0= 0.
103. Две автомашины движутся по дорогам, угол между которыми a=60°. Скорость автомашин V1=54 км/ч и V2=72км/ч. С какой скоростью V удаляются машины одна от другой?
104. Материальная точка движется прямолинейно с начальной скоростью V0=10 м/с и постоянным ускорением а=-5м/с 2 . Определить, во сколько раз путьΔs,пройденный материальной точкой, будет превышатьмодуль ее перемещения Δr спустя t=4c после начала отсчета времени.
105. Велосипедистехал из одного пункта в другой. Первую треть пути он проехал со скоростью V1=18 км/ч. Далее половину оставшегося времени он ехал со скоростью V2=22 км/ч, после чего до конечного пункта он шел пешком со скоростью V3=5км/ч. Определить среднюю скорость V велосипедиста.
106. Тело брошено под углом a = 30 о к горизонту со скоростью vo = 30 м/с. Каковы будут нормальное an и тангенциальное at ускорения тела через время t = 1 с после начала движения.
107. Материальная точка движется по окружности с постоянной угловой скоростью w = p/6 рад/с. Во сколько раз путь Ds, пройденный точкой за время t = 4 с, будет больше модуля ее перемещения Dr? Принять, что в момент начала отсчета времени радиус-вектор r, задающий положение точки на окружности, относительно исходного положения был повернут на угол jо = p/3 рад.
108. Материальная точка движется в плоскости ху согласно уравнениям х = А1 + В1 t + С1 t 2 и у = А2 + В2 t + С2 t 2 , где В1 = 7 м/с, С1 = — 2 м/с 2 , В2 = — 1 м/с, С2 = 0,2 м/с 2 . Найти модули скорости и ускорения точки в момент времени t = 5 с.
109. По краю равномерно вращающейся с угловой скоростью w = 1 рад/с платформы идет человек и обходит платформу за время
t = 9,9 с. Каково наибольшее ускорение а движения человека относительно Земли? Принять радиус платформы R = 2 м.
110.Точка движется по окружности радиусом R = 30 см с постоянным угловым ускорением e. Определить тангенциальное ускорение at точки, если известно, что за время t = 4 с она совершила три оборота и в конце третьего оборота ее нормальное ускорение
111. При горизонтальном полете со скоростью V=250 м/с снаряд массой m=8кг разорвался на две части. Большая часть массой m1=6 кг получила скорость U1=400м/c в направлении полета снаряда. Определить модуль и направление скорости U2 меньшей части снаряда.
112. С тележки, свободно движущейся по горизонтальному пути со скоростью V1=3 м/с, в сторону, противоположную движению тележки, прыгает человек, после чего скорость тележки изменилась и стала равной U1=4 м/с. Определить горизонтальную составляющую скорости U2x человека при прыжке относительно тележки. Масса тележки m1=210кг, масса человека m2=70 кг.
113. Орудие, жестко закрепленное на железнодорожной платформе, производит выстрел вдоль полотна железной дороги под углом a=30° к линии горизонта. Определить скорость U2 отката платформы, если снаряд вылетает со скоростью U1=480м/c. Масса платформы с орудием и снарядами m2=18т, масса снаряда m1=60 кг.
114. Человек массой m1=70 кг, бегущий со скоростью V1=9 км/ч, догоняет тележку массой m2=190кг, движущуюся со скоростью V2=3,6 км/ч, и вскакивает на нее. С какой скоростью станет двигаться тележка с человеком? С какой скоростью будет двигаться тележка с человеком, если человек до прыжка бежал навстречу тележке?
115. Конькобежец, стоя на коньках на льду, бросает камень массой m1=2,5 кг под углом a=30° к горизонту со скоростью V=10 м/с. Какова будет начальная скорость V0 движения конькобежца, если масса его m2=60 кг? Перемещением конькобежца во время броска пренебречь.
116. На полу стоит тележка в виде длинной доски, снабженной легкими колесами. На одном конце доски стоит человек. Масса его m1=60 кг, масса доски m2=20 кг. С какой скоростью (относительно пола) будет двигаться тележка, если человек пойдет вдоль нее со скоростью (относительно доски) V=1 м/с? Массой колес и трением пренебречь.
117. Снаряд, летевший со скоростью V = 400 м/с, в верхней точке траектории разорвался на два осколка. Меньший осколок, масса которого составляет 40% от массы снаряда, полетел в противоположном направлении со скоростью U1=150 м/с. Определить скорость U2 большего осколка.
118. Две одинаковые лодки массами m=200кг каждая (вместе с человеком и грузами, находящимися в лодках) движутся параллельными курсами навстречу друг другу с одинаковыми скоростями V=1 м/с. Когда лодки поравнялись, то с первой лодки на вторую и со второй на первую одновременно перебрасывают грузы массами m1=200 кг. Определить скорости U1 и U2 лодок после перебрасывания грузов.
119. На сколько переместится относительно берега лодка длиной l=3,5м и массой m1=200 кг, если стоящий на корме человек массой m2=80 кг переместится на нос лодки? Считать лодку расположенной перпендикулярно берегу.
120. Лодка длиной 1=3 м и массой т=120 кг стоит на спокойной воде. На носу и корме находятся два рыбака массами т1=60 кг и т2=90 кг. На сколько сдвинется лодка относительно воды, если рыбаки поменяются местами?
121. В деревянный шар массой т1=8 кг, подвешенный на нити длиной l=1,8 м, попадает горизонтально летящая пуля массой т2= 4 г. С какой скоростью летела пуля, если нить с шаром и застрявшей в нем пулей отклонилась от вертикали на угол a=3°? Размером шара пренебречь. Удар пули считать прямым, центральным.
122. По небольшому куску мягкого железа, лежащему на наковальне массой т1=300 кг, ударяет молот массой т2 = 8 кг. Определить КПД h удара, если удар неупругий. Полезной считать энергию, затраченную на деформацию куска железа.
123. Шар массой m1=1 кг движется со скоростью V1= 4 м/с и сталкивается с шаром массой т2=2 кг, движущимся навстречу ему со скоростью V2=3 м/с. Каковы скорости и1 и u2 шаров после удара? Удар считать абсолютно упругим, прямым, центральным.
124. Шар массой т1=3 кг движется со скоростью V1=2 м/с и сталкивается с покоящимся шаром массой т2 = 5 кг. Какая работа будет совершена при деформации шаров? Удар считать абсолютно неупругим, прямым, центральным.
125. Определить КПДh неупругого удара бойка массой т1=0,5 т, падающего на сваю массой т2=120 кг. Полезной считать энергию, затраченную на вбивание сваи.
126. Шар массой т1=4 кг движется со скоростью V1= 5 м/с и сталкивается с шаром массой m2 =6 кг, который движется ему навстречу со скоростью V2= 2 м/с. Определить скорости u1 и u2 шаров после удара. Удар считать абсолютно упругим, прямым, центральным.
127. Из ствола автоматического пистолета вылетела пуля массой m1 = 10 г со скоростью V = 300 м/с. Затвор пистолета массой m2 = 200 г прижимается к стволу пружиной, жесткость которой k=25 кН/м.На какое расстояние отойдет затвор послевыстрела? Считать, что пистолет жестко закреплен.
128. Шар массой т1 = 5 кг движется со скоростью V1 = 1 м/с и сталкивается с покоящимся шаром массой т2 = 2 кг. Определить скорости u1 и u2 шаров после удара. Удар считать абсолютно упругим, прямым, центральным.
129. Из орудия, не имеющего противооткатного устройства, производилась стрельба в горизонтальном направлении. Когда орудие было неподвижно закреплено, снаряд вылетел со скоростью V1 = 600 м/с, а когда орудию дали возможность свободно откатываться назад, снаряд вылетел со скоростью V2 = 580 м/с. С какой скоростью откатилось при этом орудие?
130. Шар массой т1 = 2 кг сталкивается с покоящимся шаром большей массы и при этом теряет 40% кинетической энергии. Определить массу т2 большего шара. Удар считать абсолютно упругим, прямым, центральным.
131. Определить работу растяжения двух соединенных последовательно пружин жесткостями k1 = 400 Н/м и k2 = 250 Н/м, если первая пружина при этом растянулась на Dl = 2 см.
132. Из шахты глубиной h = 600 м поднимают клеть массой т1 = 3,0 т на канате, каждый метр которого имеет массу m = 1,5 кг. Какая работа A совершается при поднятии клети на поверхность Земли? Каков коэффициент полезного действия h подъемного устройства?
133. Пружина жесткостью k = 500 Н/м сжата силой F = 100 H. Определить работу A внешней силы, дополнительно сжимающей пружину еще на Dl = 2 см.
134. Две пружины жесткостью k1 = 0,5 кН/м и k2 = 1 кН/м скреплены параллельно. Определить потенциальную энергию П данной системы при абсолютной деформации Dl = 4 см.
135. Какую нужно совершить работу A, чтобы пружину жесткостью k = 800 Н/м, сжатую на х= 6 см, дополнительно сжать на Dx = 8 см?
136. Если на верхний конец вертикально расположенной спиральной пружины положить груз, то пружина сожмется на Dl = 3 мм. На сколько сожмет пружину тот же груз, упавший на конец пружины с высоты h = 8 см?
137. Из пружинного пистолета с пружиной жесткостью k = 150 Н/м был произведен выстрел пулей массой m = 8 г. Определить скорость V пули при вылете ее из пистолета, если пружина была сжата на Dx = 4 см.
138. Налетев на пружинный буфер, вагон массой m = 16 т, двигавшийся со скоростью V = 0,6м/с, остановился, сжав пружину на Dl = 8 см. Найти общую жесткость k пружин буфера.
139. Цепь длиной l == 2 м лежит на столе, одним концом свисая со стола. Если длина свешивающейся части превышает ‘/зl, то цепь соскальзывает со стола. Определить скорость V цепи в момент ее отрыва от стола.
140. Какая работа А должна быть совершена при поднятии с земли материалов для постройки цилиндрической дымоходной трубы высотой h = 40 м, наружным диаметром D = 3,0 м и внутренним диаметром d = 2,0 м? Плотность материала r принять равной 2,8×10 3 кг/м 3 .
141.Определить напряженность G гравитационного поля на высоте h = 1000 км над поверхностью Земли. Считать известными ускорение g свободного падения у поверхности Земли и ее радиус R.
142. Какая работа А будет совершена силами гравитационного поля при падении на Землю тела массой m = 2 кг:
1) с высоты h = 1000 км; 2) из бесконечности?
143. Из бесконечности на поверхность Земли падает метеорит массой m = 30 кг. Определить работу А, которая при этом будет совершена силами гравитационного поля Земли. Ускорение свободного падения g у поверхности Земли и ее радиус R считать известными.
144.С поверхности Земли вертикально вверх пущена ракета со скоростью v=5 км/с. На какую высоту она поднимется?
145.По круговой орбите вокруг Земли обращается спутник с периодом Т = 90 мин. Определить высоту спутника. Ускорение свободного падения g у поверхности Земли и ее радиус R считать известными.
146.На каком расстоянии от центра Земли находится точка, в которой напряженность суммарного гравитационного поля Земли и Луны равна нулю? Принять, что масса Земли в 81 раз больше массы Луны и что расстояние от центра Земли до центра Луны равно 60 радиусам Земли.
147.Спутник обращается вокруг Земли по круговой орбите на высоте h=520 км. Определить период обращения спутника. Ускорение свободного падения g у поверхности Земли и ее радиус R считать известными.
148. Определить линейную и угловую скорости спутника Земли, обращающегося по круговой орбите на высоте h =1000 км. Ускорение свободного падения g у поверхности Земли и ее радиус R считать известными.
149.Какова масса Земли, если известно, что Луна в течение года совершает 13 обращений вокруг Земли и расстояние от Земли до Луны равно 3,84×10 8 м.
150.Во сколько раз средняя плотность земного вещества отличается от средней плотности лунного? Принять, что радиус Rз Земли в 390 раз больше радиуса Rл Луны и вес тела на Луне в 6 раз меньше веса тела на Земле.
Дата добавления: 2014-10-31 ; просмотров: 63 ; Нарушение авторских прав
- Примеры решения задач. 1. Частица движется вдоль прямой по закону x=A+Bt+Ct3 , где А=3 м, В=2,5 м/с, С=0,25м/c3
- Примеры решения задач по теме №1
- Тело движется вдоль оси X так, что зависимость координаты от времени задана уравнением: x = A + Bt + Ct2. Найти среднюю скорость тела и ускорение за промежуток времени 1-4 с, если A = 6 м, B = -3 м/с
- Описание и исходные данные задания, 50% решения + фотография:
- 🔥 Видео
Видео:Урок 87. Движение по наклонной плоскости (ч.1)Скачать

Примеры решения задач. 1. Частица движется вдоль прямой по закону x=A+Bt+Ct3 , где А=3 м, В=2,5 м/с, С=0,25м/c3
1. Частица движется вдоль прямой по закону x=A+Bt+Ct 3 , где А=3 м, В=2,5 м/с, С=0,25м/c 3 . Найти средние значения скорости и ускорения за интервал времени от t1=1 с до t2=6 с.
| Дано: | Решение: |
| x=A+Bt+Ct 3 А=3 м В=2,5 м/с С=0,25м/c 3 t1=1 с t2=6 с | Средняя скорость это отношение перемещения к промежутку времени, за которое это перемещение произошло, тогда модуль средней скорости равен: 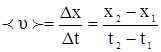 , где , где  =3+2,5×1+0,25×1 3 =5,75 м =3+2,5×1+0,25×1 3 =5,75 м |
| Найти: — ? — ? | 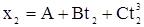 =3+2,5×6+0,25×6 3 =72 м Средняя скорость: =3+2,5×6+0,25×6 3 =72 м Средняя скорость:  |
Среднее ускорение это отношение изменения скорости к промежутку времени, за который это изменение произошло, тогда модуль среднего ускорения равен:  , где , где    Среднее ускорение: Среднее ускорение:  Ответ: Ответ:  ; ; 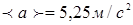 . . |
2. Тело вращается вокруг неподвижной оси по закону 
| Дано: | Решение: |
 r=0,1 м t=4 с r=0,1 м t=4 с | Угловая скорость w вращающегося тела равна первой производной от угла поворота от времени: 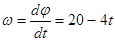 |
| Найти:а — ? | В момент времени t=4 с: w=20-4×4=4 рад/с |
 | Угловое ускорение e вращающегося тела равно первой производной от угловой скорости по времени:  рад/с 2 Материальная точка, принадлежащая телу, движется по окружности радиуса r. Движение материальной точки ускоренное с постоянным угловым ускорением (e=const). Следовательно, тангенциальное ускорение аt будет посто- янным, а нормальное ускорение аn непрерывно возрастаетсо временем, т.е. вектор полного ускорения точки со временем изменяется как по модулю, так и по направлению. Полное ускорение точки, движущейся по окружности, может быть найдено как геометрическая сумма тангенциального ускорения рад/с 2 Материальная точка, принадлежащая телу, движется по окружности радиуса r. Движение материальной точки ускоренное с постоянным угловым ускорением (e=const). Следовательно, тангенциальное ускорение аt будет посто- янным, а нормальное ускорение аn непрерывно возрастаетсо временем, т.е. вектор полного ускорения точки со временем изменяется как по модулю, так и по направлению. Полное ускорение точки, движущейся по окружности, может быть найдено как геометрическая сумма тангенциального ускорения  , направленного по касательной к траектории и нормального ускорения , направленного по касательной к траектории и нормального ускорения  , направленного к центру кривизны траектории. Модуль полного ускорения: , направленного к центру кривизны траектории. Модуль полного ускорения:  (1) (1) |
Тангенциальное ускорение точки вращающегося тела выражается формулой: аt=e×r, (2) где e — угловое ускорение тела. Нормальное ускорение точки вращающегося тела выражается формулой: аn=w 2 r, (3) где w — угловая скорость тела. Подставив выражения (2) и (3) в формулу (1), получаем  (4) (4) | |
Подставив найденные значения w и e и заданное значение r в формулу (4), получим:  м/с 2 Направление полного ускорения определится, если найти угол, который вектор ускорения образует с нормалью к траектории (см. рис.): м/с 2 Направление полного ускорения определится, если найти угол, который вектор ускорения образует с нормалью к траектории (см. рис.):  или или  (5) По формулам (2) и (3) найдем значения (5) По формулам (2) и (3) найдем значения  и и 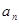 : :  =-0,4 м/с 2 , =-0,4 м/с 2 , 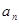 =1,6 м/с 2 . Подставив эти значения и значение полного ускорения в формулы (5), получим: cosa=0,97, sina=0,24. =1,6 м/с 2 . Подставив эти значения и значение полного ускорения в формулы (5), получим: cosa=0,97, sina=0,24. | |
| Пользуясь тригонометрическими таблицами или калькулятором, найдем значение угла a: a»14°. Ответ: a=1,65 м/с 2 , a»14°. |
3. Автомашина массой m=1,8 т движется в гору, уклон которой составляет 3 м на каждые 100 м пути, и за 5 мин преодолевает путь S=5 км. Определить: 1) работу, совершаемую двигателем автомашины, если коэффициент трения равен 0,1; 2) развиваемую двигателем мощность.
| Дано: | Решение: |
| m=1,8 т=1800 кг h=3 м l=100 м t=5 мин=300 с S=5 км=5000 м m=0,1 |  Сделаем рисунок. Покажем, какие силы действуют на автомашину. Сделаем рисунок. Покажем, какие силы действуют на автомашину. |
| Найти: A-? P-? | Уравнение движения автомашины в векторной форме:  |
Запишем это уравнение в проекциях на оси x и y (см. рис.): ox:  oy: oy:  Из последнего Из последнего  , тогда , тогда 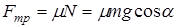 . Сила тяги двигателя автомашины будет равна: . Сила тяги двигателя автомашины будет равна:  Работа, совершаемая двигателем автомашины: Работа, совершаемая двигателем автомашины:  , где , где  , ,  , ,  Подставляем числовые значения и получаем: Подставляем числовые значения и получаем:  = =12,7 МДж Средняя мощность, развиваемая двигателем автомашины: = =12,7 МДж Средняя мощность, развиваемая двигателем автомашины:  кВт кВт | |
Максимальная мощность, развиваемая двигателем автомашины:  , где , где  Подставляем числовые значения и получаем: Подставляем числовые значения и получаем:  84 кВт Ответ: A=12,7 МДж; áPñ=42 кВт; Pmax=84 кВт. 84 кВт Ответ: A=12,7 МДж; áPñ=42 кВт; Pmax=84 кВт. |
4. Шар массой m1=3 кг движется со скоростью u1=2 м/с и сталкивается с покоящимся шаром массой m2=5 кг. Какая работа будет совершена при деформации шаров? Удар считать абсолютно неупругим, прямым, центральным.
| Дано: | Решение: |
| m1=3 кг u1=2 м/с m2=5 кг | Работа будет равна изменению кинетической энергии системы: 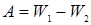 , (1) , (1) |
| Найти: A — ? | где кинетическая энергия шаров до столкновения:  (2) (2) |
Она равна кинетической энергии первого шара, т.к. второй шар покоится. 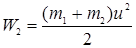 (3) кинетическая энергия шаров после столкновения. Здесь скорость u – скорость системы двух шаров после столкновения. Для ее определения воспользуемся законом сохранения импульса: (3) кинетическая энергия шаров после столкновения. Здесь скорость u – скорость системы двух шаров после столкновения. Для ее определения воспользуемся законом сохранения импульса:   (4) Из выражений (1) – (4) окончательно получаем: (4) Из выражений (1) – (4) окончательно получаем:  Подставляем числовые значения и получаем: Подставляем числовые значения и получаем:  Дж Ответ: А=3,74 Дж Дж Ответ: А=3,74 Дж |
5. Камень брошен со скоростью u0=15 м/с под углом a=60° к горизонту. Найти кинетическую, потенциальную и полную энергии камня: а) через 1 с после начала движения; б) в высшей точке траектории. Масса камня m=0,2 кг.
| Дано: | Решение: |
| u0=15 м/с a=60° t=1 с m=0,2 кг | Движение камня сложное, криволинейное: вдоль оси OX равномерное с постоянной скоростью  , (1) а вдоль оси OY равнопеременное с постоянным ускорением g=9,8 м/с 2 :. , (1) а вдоль оси OY равнопеременное с постоянным ускорением g=9,8 м/с 2 :. |
| Найти: Wк — ? Wп — ? W — ? | 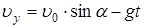 (2) (2) |
 | |
Через t=1 с скорость камня будет равна:  (3) (3) | |
Кинетическая энергия камня через t=1 с будет равна:  Найдем на какой высоте окажется камень через t=1 с: Найдем на какой высоте окажется камень через t=1 с:  Тогда потенциальная энергия камня в этот момент равна: Тогда потенциальная энергия камня в этот момент равна:  Полная механическая энергия камня через t=1 с равна: Полная механическая энергия камня через t=1 с равна:  В верхней точке траектории В верхней точке траектории  , следовательно, полная скорость в этой точке равна: , следовательно, полная скорость в этой точке равна:  . Тогда кинетическая энергия в верхней точке траектории равна: . Тогда кинетическая энергия в верхней точке траектории равна: 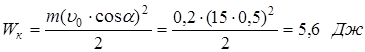 Чтобы найти потенциальную энергию в верхней точке траектории, найдем максимальную высоту подъема. Чтобы найти потенциальную энергию в верхней точке траектории, найдем максимальную высоту подъема. | |
Для этого найдем время подъема. В верхней точке траектории  , следовательно, , следовательно,  Отсюда получаем время подъема: Отсюда получаем время подъема:  Зная время подъема, можно найти максимальную высоту подъема: Зная время подъема, можно найти максимальную высоту подъема:  Найдем потенциальную энергию в верхней точке траектории: Найдем потенциальную энергию в верхней точке траектории: | |
 Полная механическая энергия камня в верхней точке траектории равна: Полная механическая энергия камня в верхней точке траектории равна:  Видно, что выполняется закон сохранения механической энергии: полная механическая энергия камня в верхней точке траектории равна полной механической энергии камня через 1 с после начала полета. Ответ: Wк=5,6 Дж; Wп=16,9 Дж; W=22,5 Дж. Видно, что выполняется закон сохранения механической энергии: полная механическая энергия камня в верхней точке траектории равна полной механической энергии камня через 1 с после начала полета. Ответ: Wк=5,6 Дж; Wп=16,9 Дж; W=22,5 Дж. |
6. Две гири с массами m1=2 кг и m2=1 кг соединены нитью, перекинутой через блок массой m=1 кг. Найти ускорение, с которым движутся гири, и силы натяжения нитей, к которым подвешены гири. Блок считать однородным диском. Трением пренебречь.
| Дано: | Решение: |
| m1=2 кг m2=1 кг m=1 кг | Запишим уравнения движения гирь:  |
| Найти: a — ? Т1 — ? Т2 — ? |  |
 | Запишим эти уравнения в проекциях на ось Y:  (1) (1)  (2) Нить будет натянута по обе стороны блока по-разному, и разность сил натяжения будет создавать момент сил, вращающий блок. Запишим основной закон динамики: (2) Нить будет натянута по обе стороны блока по-разному, и разность сил натяжения будет создавать момент сил, вращающий блок. Запишим основной закон динамики:  , (3) , (3) |
где  , а , а  — момент инерции блока. Решая (1) — (3) совместно, найдем — момент инерции блока. Решая (1) — (3) совместно, найдем  м/с 2 (4) м/с 2 (4) | |
Подставляя (4) в (1) и (2), получим  =14 Н =14 Н  =12,6 Н Ответ: a=2,8 м/с 2 ; T1=14 Н; T2=12,6 Н. =12,6 Н Ответ: a=2,8 м/с 2 ; T1=14 Н; T2=12,6 Н. |
7. Платформа в виде диска радиусом R=1,5 м и массой m1=180 кг вращается по инерции вокруг вертикальной оси, делая n=1/6 с -1 . В центре платформы стоит человек массой m2=60 кг. Какую линейную скорость относительно пола помещения будет иметь человек, если он перейдет на край платформы?
| Дано: | Решение: |
| R=1,5 м m1=180 кг n=1/6 с -1 m2=60 кг | По закону сохранения момента импульса:  , (1) где Jпл, Jчел – моменты инерции платформы и стоящего в ее центре человека; w1 – угловая скорость платформы с , (1) где Jпл, Jчел – моменты инерции платформы и стоящего в ее центре человека; w1 – угловая скорость платформы с |
| Найти: u — ? | человеком, стоящим в ее центре;  — момент инерции человека, стоящего на краю платформы; w2 – угловая скорость платформы с человеком, стоящим на ее краю. Линейная скорость человека, стоящего на краю платформы, связана с угловой скоростью соотношением: u=w2R (2) Определив из уравнения (1) w2 и подставив полученное выражение в (2), будем иметь: — момент инерции человека, стоящего на краю платформы; w2 – угловая скорость платформы с человеком, стоящим на ее краю. Линейная скорость человека, стоящего на краю платформы, связана с угловой скоростью соотношением: u=w2R (2) Определив из уравнения (1) w2 и подставив полученное выражение в (2), будем иметь:  (3) (3) |
Момент инерции платформы определим как для диска:  Момент инерции человека рассчитываем как для материальной точки: Момент инерции человека рассчитываем как для материальной точки:  , ,  | |
Угловая скорость платформы до перехода человека из центра на край платформы: w=2pn. Заменив в формуле (3) величины Jпл, Jчел,  , и w2 их выражениями, получим: , и w2 их выражениями, получим: | |
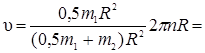  Подставляем числовые значения и получаем: Подставляем числовые значения и получаем: 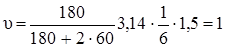 м/с Ответ: u=1 м/с. м/с Ответ: u=1 м/с. |
8. К пружине подвешен груз массой m=10 кг, который совершает колебания с амплитудой 5 см. Зная, что пружина под влиянием силы F=9,8 Н растягивается на l=1,5 см, найти: частоту, период и циклическую частоту вертикальных колебаний пружины, жесткость пружины, полную энергию, максимальную скорость и максимальное ускорение.
| Дано: | Решение: |
| m=10 кг А=5 см=0,05 м F=9,8 Н l=1,5 см=0,015 м | Уравнение гармонических колебаний пружинного маятника имеет вид:  , (1) где s – смещение маятника от положения равновесия; , (1) где s – смещение маятника от положения равновесия; |
| Найти: n — ? T — ? w — ? k — ? W — ? umax — ? amax — ? | А – амплитуда колебаний; w=2pn – циклическая частота;  — частота колебаний; Т – период колебаний; j0 – начальная фаза. — частота колебаний; Т – период колебаний; j0 – начальная фаза. |
Из закона Гука F=kl найдем коэффициент жесткости пружины: 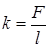 ; ;  653 Н/м Зная коэффициент жесткости пружины, найдем период колебаний груза на пружине: 653 Н/м Зная коэффициент жесткости пружины, найдем период колебаний груза на пружине:  ; ;  с Следовательно, частота и циклическая частота соответст венно равны: с Следовательно, частота и циклическая частота соответст венно равны: | |
 ; ;  Гц; w=2pn=2×3,14×1,25=7,85 с -1 Гц; w=2pn=2×3,14×1,25=7,85 с -1 | |
Скорость колебаний:  , (2) где umax=Аw — максимальная скорость колебаний. umax=0,05×7,85=0,4 м/с Ускорение маятника: , (2) где umax=Аw — максимальная скорость колебаний. umax=0,05×7,85=0,4 м/с Ускорение маятника:  , (3) где , (3) где  — максимальное ускорение. — максимальное ускорение.  м/с 2 Полная энергия маятника: м/с 2 Полная энергия маятника:   Дж Ответ: k=653 Н/м; Дж Ответ: k=653 Н/м;  Гц; Т=0,8 с; w=7,85 с -1 ; umax=0,4 м/с; Гц; Т=0,8 с; w=7,85 с -1 ; umax=0,4 м/с; 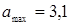 м/с 2 ; W=0,77 Дж. м/с 2 ; W=0,77 Дж. |
9. Волна распространяется в упругой среде со скоростью 150 м/с. Определить частоту колебаний, если минимальное расстояние между точками среды, фазы колебаний которых противоположны равно 0,75 м.
Видео:ЕГЭ по математике. Профильный уровень. Задание 7. Закон движения. ПроизводнаяСкачать

Примеры решения задач по теме №1
«Механика и элементы специальной теории относительности»
Задача 1 Уравнение движения точки по прямой имеет вид: x = A+Bt+Ct 3 , где А = 4 м, В = 2 м/c, С = 0,2 м/с 3 . Найти: 1) положение точки в моменты времени t = 2 c и t = 5 с; 2) среднюю скорость за время, протекшее между этими моментами; 3) мгновенные скорости в указанные моменты времени; 4) среднее ускорение за указанный промежуток времени; 5) мгновенные ускорения в указанные моменты времени.
| x = A + Bt + Ct 3 A = 4 м B = 2 м/c C = 0,2 м/c 3 t1 = 2 c; t2 = 5 c | Решение 1. Чтобы найти координаты точки, надо в уравнение движения подставить значения t1 и t2: x1 = (4+2×2+0,2×2 3 ) м = 9,6 м, x2 = (4+2×5+0,2×5 3 ) м = 39 м. |
| x1, x2, — ? u1, u2 — ? , a1, a2 — ? | 2. Средняя скорость  , , |

3. Мгновенные скорости найдем, продифференцировав по времени уравнение движения:
u1 = (2+3×0,2×2 2 ) м/с = 4,4 м/c;
u2 = (2+3×0,2×5 2 ) м/с = 17 м/с.
4. Среднее ускорение 
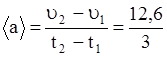
5. Мгновенное ускорение получим, если продифференцируем по времени выражение для скорости: a = 2×3×Ct = 6Ct.
a1 = 6×0,2×2 м/c 2 = 2,4 м/с 2 ;
a2 = 6×0,2×5 м/с 2 = 6 м/с 2 .
Ответ: x1 = 9,6 м; x2 = 39 м; áuñ = 9,8 м/с; u1 = 4,4 м/c; u2 = 17 м/с; áаñ = 4,2 м/с 2 ; a1 = 2,4 м/с 2 ; a2 = 6 м/с 2 .
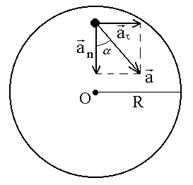
Задача 2 Маховик вращается равноускоренно. Найти угол a, который составляет вектор полного ускорения 
| w0 = 0 N = 2 e = const | Решение Разложив вектор  точки М на тангенциальное точки М на тангенциальное  и нормальное и нормальное  ускорения, видим, что искомый угол определяется соотношением tga=at/an. ускорения, видим, что искомый угол определяется соотношением tga=at/an. |
| a — ? |
Поскольку в условии дано лишь число оборотов, перейдем к угловым величинам. Применив формулы: at = eR, an = w 2 R, где R – радиус маховика, получим
так как маховик вращается равноускоренно, найдем связь между величинами e и w;
Поскольку w0 = 0; j = 2pN, то w 2 = 2e×2pN = 4pNe.
Подставим это значение в формулу, получим:

Задача 3 Две гири с массами m1 = 2 кг и m2 = 1 кг соединены нитью, перекинутой через невесомый блок. Найти ускорение a, с которым движутся гири, и силу натяжения нити 
| m1 = 2 кг m2 = 1 кг | Решение Воспользуемся для решения задачи основным законом динамики  где где  – равнодействующая всех сил, действующих на тело. – равнодействующая всех сил, действующих на тело. |
| a, FН — ? |
На тело 1 и тело 2 действуют только две силы – сила тяжести и сила
натяжения нити. Для первого тела имеем

 |
для второго тела

Так как сила трения в блоке отсутствует,

Ускорения тел а1 и а2 направлены в противоположные стороны и равны по модулю:

Получаем из выражений (1) и (2) систему уравнений
Выберем ось Х, как показано на рисунке и запишем полученную систему уравнений
в проекции на ось Х
Решая эту систему относительно а и FН, получаем:


Ответ: a= 3,3 м/c 2 ; FH = 13 Н.
Задача 4 К ободу однородного диска радиусом R=0,2 м приложена касательная сила F=98,1 Н. При вращении на диск действует момент сил трения
МТР=4,9 Н×м. Найти массу m диска, если известно, что диск вращается с угловым ускорением e=100 рад/с 2 .
| R = 0,2 м F = 98,1 Н MТР = 4,9 Н×м e = 100 рад / c 2 | Решение Воспользуемся основным законом динамики вращательного движения, записанным для оси вращения, направление которой совпадает с направлением угловой скорости:  , где , где  — момент сил, приложенных к телу, — момент сил, приложенных к телу, |
| m — ? |
относительно выбранной оси ( MF — момент силы F, Mтр – момент сил трения);

Учитывая, что MF=F×R, получаем 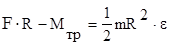
Отсюда 
Задача 5 На гладкой горизонтальной поверхности находятся две одинаковые соприкасающиеся шайбы. Третья такая же шайба налетает на них со скоростью v0 = 6 м/с, направленной по общей касательной к неподвижным шайбам. После столкновения налетевшая шайба движется вдоль первоначального направления со скоростью v1 = 2 м/с. Найти величину энергии, перешедшей во внутреннюю энергию тел при столкновении. Масса каждой шайбы m = 100 г.



Поскольку размеры всех шайб одинаковы, то скорости v2 и v3, направленные вдоль прямых,
соединяющих центры шайб в момент удара, составляют одинаковые углы a = 30 о с осью X, а так как массы всех шайб по условию равны, то очевидно, что скорости v2 и v3 равны по модулю, то есть v2 = v3 = v.
Теперь запишем закон сохранения импульса для проекций импульсов взаимодействующих тел на ось X:
Тогда mv0 = mv1 + 2 mv сosa.
Отсюда 
Энергию, перешедшую во внутреннюю энергию тел при частично неупругом ударе, можно найти как разность кинетической энергии налетающей шайбы до удара и суммарной кинетической энергии всех тел после удара:

Ответ: DU = 1,07 Дж.
Задача 6 Небольшое тело массой m равномерно втащили на горку, действуя силой, которая в каждой точке направлена по касательной к траектории. Найти работу этой силы, если высота горки h, длина ее основания l, и коэффициент трения m.

Работу, совершаемую силой 

Для этого необходимо предварительно найти силу 




Выберем координатные оси х и у таким образом, чтобы ось х была направлена по касательной к траектории (вдоль перемещения 
Запишем векторное равенство в проекциях на эти координатные оси:
oсь x:
oсь y:
Тогда 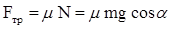

Теперь можно найти выражение для элементарной работы, совершаемой силой F при перемещении тела на расстояние dr. При этом учтем, что угол между векторами 

Тогда 
Из рис. видно, что 

Тогда 
и полная работа, совершаемая силой F при втаскивании тела на горку:


Ответ: 
Задача 7 Круглая платформа радиусом R=1,0 м, момент инерции которой J=130 кг×м 2 , вращается по инерции вокруг вертикальной оси, делая n1=1,0 об/с. На краю платформы стоит человек, масса которого m=70 кг. Сколько оборотов в секунду n2 будет совершать платформа, если человек перейдет в её центр? Момент инерции человека рассчитывать как для материальной точки.
| R = 1м J = 130 кг × м 2 n1 = 1c -1 m = 70 кг | Решение Согласно условию задачи, платформа с человеком вращается по инерции. Это означает, что результирующий момент всех внешних сил, приложенных к вращающейся системе, равен нулю. Следовательно, для системы “платформа + человек” выполняется закон сохранения момента импульса, который запишем в скалярной форме относительно оси, совпадающей с осью вращения и направленной по угловой скорости: |
| n2 — ? |
где L1 — импульс системы «платформа + человек на краю платформы», L2 — импульс системы «платформа + человек в центре платформы».
где mR 2 — момент инерции человека, J1 = J+mR 2 — момент инерции системы «платформа + человек на краю платформы», J2 — момент инерции системы «платформа + человек в центре платформы», w1 и w2 — соответствующие угловые скорости системы. Решая систему уравнений (1) — (3), получаем
Задача 8 В условно неподвижной системе отсчета К в точках с координатами xA и xB = xA + l, где l = 1 км, одновременно происходят два события A и B. На каком расстоянии l¢АВ друг от друга зафиксирует эти события наблюдатель в системе К¢, движущейся со скоростью v = 0,4×с вдоль оси X? Какой промежуток времени Dt¢ между этими событиями зафиксирует наблюдатель в системе К¢?

Обозначим через t0 момент времени, когда в системе К происходят события А и В. Тогда событие А в этой системе обладает пространственно – временными координатами xA и t0, а событие В – координатами xB и t0. В системе К¢ событие А обладает пространственно–временными координатами x1¢ и t1¢, а событие В – координатами x2¢ и t2¢. Связь координат каждого из событий можно записать с помощью преобразований Лоренца.
Найдя разность этих выражений, получим расстояние между точками, в которых происходят события А и В в системе К¢.
Видно, что расстояние l¢АВ, разделяющее события А и В в любой системе, движущейся относительно К, больше, чем это же расстояние, измеренное в системе К, в которой оба события одновременны. Рассчитаем расстояние l¢АВ.
Моменты времени, в которые в системе К¢ наблюдатель зафиксирует события А и В, также могут быть найдены из преобразований Лоренца:
Видно, что события А и В в системе отсчета К¢ не являются одновременными. Если xB > xA и система К¢ движется в положительном направлении оси X, как и задано в условии, то t2¢ — t1¢ .
Видео:Урок 37. Движение тела, брошенного под углом к горизонту (начало)Скачать

Тело движется вдоль оси X так, что зависимость координаты от времени задана уравнением: x = A + Bt + Ct2. Найти среднюю скорость тела и ускорение за промежуток времени 1-4 с, если A = 6 м, B = -3 м/с






Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.
Кстати, если эта работа не по вашей теме или не по вашим данным , не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу , я смогу выполнить её в срок 1-3 дня!
Описание и исходные данные задания, 50% решения + фотография:
№2-1(1) 2. Тело движется вдоль оси X так, что зависимость координаты от времени задана уравнением: x = A + Bt + Ct2. Найти среднюю скорость тела и ускорение за промежуток времени 1-4 с, если A = 6 м, B = -3 м/с и C = 2 м/с2.
Найдём закон изменения скорости тела: , или с учётом числовых значений: (м/с). Определим момент времени , в который скорость тела станет равна нулю: с. Таким образом, начиная с момента времени 0,75 с тело будет двигаться в одну сторону – в положительном направлении оси X. Тогда средняя скорость тела будет определяться выражением: , где – изменение координаты тела за время .
| Если вам нужно решить физику, тогда нажмите ➔ заказать физику. |
| Похожие готовые решения: |
- Зависимость пройденного телом пути от времени даётся уравнением s = A – Bt + Ct2, где А = 6 м, В = 3 м/c и С = 2 м/c2. Найти среднюю скорость и среднее ускорение тела в интервале времени от 1 с до 4 с. Построить график пути, скорости и ускорения для 0 ≤ t ≤ 5 с через 1 с.
- Зависимость пройденного телом пути s от времени t даётся уравнением s = A – Bt + Ct2, где A = 6 м, B = 3 м/с и C = 2 м/с2. Найти среднюю скорость v и среднее ускорение a тела для интервала времени 1
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
🔥 Видео
Урок 14. Графическое описание РПДСкачать

Кинематика. Закон движения. Урок 3Скачать

Урок 106. Реактивное движениеСкачать

Урок 86. Движение связанных тел (ч.2)Скачать

Урок 41. Задачи на движение тела, брошенного под углом к горизонту (ч.2)Скачать

Физика 9 класс. «Движение тела под. действием нескольких сил»Скачать

Решение задач о движении связанных тел. Видеоурок 10. Физика 9 классСкачать

Урок 92. Комбинированные задачи динамики (ч.2)Скачать

Решение задач о движении тела под действием нескольких сил. Видеоурок 10. Физика 10 классСкачать

Свободное падение тел. 10 класс.Скачать

Урок 15. Решение задач на графики движенияСкачать

Урок 221. Решение комбинированных задачСкачать

Материальная точка движется вдоль оси OX по законуСкачать

Урок 85. Движение связанных тел (ч.1)Скачать

Урок 21 (осн). Задачи на одновременное движение телСкачать

Урок 3 Определение координаты движущегося телаСкачать

Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать

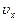 и ускорение
и ускорение 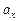 точки в момент времени t = 2с.
точки в момент времени t = 2с.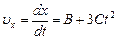 .
.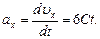
 точки, движущейся по кривой линии, может быть найдено как геометрическая сумма тангенциального ускорения
точки, движущейся по кривой линии, может быть найдено как геометрическая сумма тангенциального ускорения 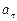 , направленного по касательной к траектории, и нормального ускорения
, направленного по касательной к траектории, и нормального ускорения 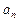 , направленного к центру кривизны траектории (рис.1):
, направленного к центру кривизны траектории (рис.1):


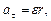

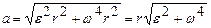 . (2)
. (2)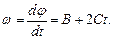
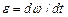 = 2 C = — 4 рад/с 2 .
= 2 C = — 4 рад/с 2 .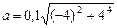 м/с = 1,65 м/с 2 .
м/с = 1,65 м/с 2 .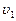 , столкнулся с неподвижным шаром массой m2. Шары абсолютно упругие, удар прямой, центральный. Какую долю e своей кинетической энергии первый шар передал второму?
, столкнулся с неподвижным шаром массой m2. Шары абсолютно упругие, удар прямой, центральный. Какую долю e своей кинетической энергии первый шар передал второму?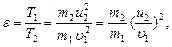 (1)
(1)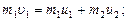 (2)
(2)
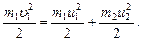 (3)
(3)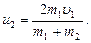
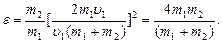
 Решение: Рассмотрим силы, действующие на каждый груз и на блок в отдельности. На каждый груз действуют две силы: сила тяжести и сила упругости (сила натяжения нити). Направим ось х вертикально вниз и напишем для каждого груза уравнение движения (второй закон Ньютона) в проекциях на эту ось. Для первого груза
Решение: Рассмотрим силы, действующие на каждый груз и на блок в отдельности. На каждый груз действуют две силы: сила тяжести и сила упругости (сила натяжения нити). Направим ось х вертикально вниз и напишем для каждого груза уравнение движения (второй закон Ньютона) в проекциях на эту ось. Для первого груза ; (1)
; (1)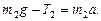 (2)
(2)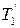 и
и 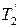 относительно оси z перпендикулярной плоскости чертежа и направленной за чертеж, блок приобретает угловое ускорение e. Согласно основному уравнению динамики вращательного движения,
относительно оси z перпендикулярной плоскости чертежа и направленной за чертеж, блок приобретает угловое ускорение e. Согласно основному уравнению динамики вращательного движения,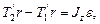 (3)
(3)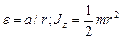 — момент инерции блока (сплошного диска) относительно оси z.
— момент инерции блока (сплошного диска) относительно оси z.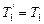 и
и  . Воспользовавшись этим подставим в уравнение (3) вместо
. Воспользовавшись этим подставим в уравнение (3) вместо 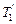 и
и 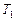 и
и 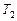 , получив их предварительно из уравнений (1) и (2):
, получив их предварительно из уравнений (1) и (2):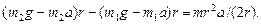
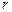 и перегруппировки членов найдем
и перегруппировки членов найдем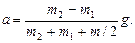 (4)
(4)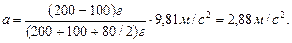

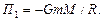

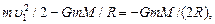
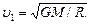
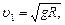
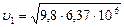 м/с = 7,9 км/с.
м/с = 7,9 км/с.