Тату уравнение дирака квантовая запутанность (2 видео)

Просто о квантовой запутанности

Квантовая запутанность – одно из самых сложных понятий в науке, но основные её принципы просты. А если понять её, запутанность открывает путь к лучшему пониманию таких понятий, как множественность миров в квантовой теории.

Чарующей аурой загадочности окутано понятие квантовой запутанности, а также (каким-то образом) связанное с ним требование квантовой теории о необходимости наличия «многих миров». И, тем не менее, по сути своей это научные идеи с приземлённым смыслом и конкретными применениями. Я хотел бы объяснить понятия запутанности и множества миров настолько просто и ясно, насколько знаю их сам.

Запутанность считается явлением, уникальным для квантовой механики – но это не так. На самом деле, для начала будет более понятным (хотя это и необычный подход) рассмотреть простую, не квантовую (классическую) версию запутанности. Это позволит нам отделить тонкости, связанные с самой запутанностью, от других странностей квантовой теории.

Запутанность появляется в ситуациях, в которых у нас есть частичная информация о состоянии двух систем. К примеру, нашими системами могут стать два объекта – назовём их каоны. «К» будет обозначать «классические» объекты. Но если вам очень хочется представлять себе что-то конкретное и приятное – представьте, что это пирожные.

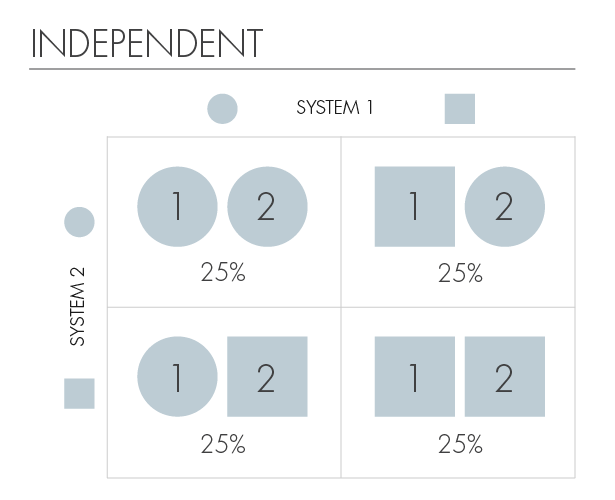
Наши каоны будут иметь две формы, квадратную или круглую, и эти формы будут обозначать их возможные состояния. Тогда четырьмя возможными совместными состояниями двух каонов будут: (квадрат, квадрат), (квадрат, круг), (круг, квадрат), (круг, круг). В таблице указана вероятность нахождения системы в одном из четырёх перечисленных состояний.

Мы будем говорить, что каоны «независимы», если знание о состоянии одного из них не даёт нам информации о состоянии другого. И у этой таблицы есть такое свойство. Если первый каон (пирожное) квадратный, мы всё ещё не знаем форму второго. И наоборот, форма второго ничего не говорит нам о форме первого.

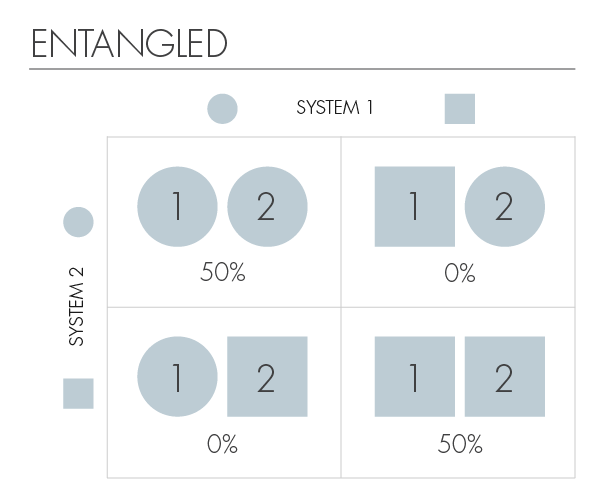
С другой стороны, мы скажем, что два каона запутаны, если информация об одном из них улучшает наши знания о другом. Вторая табличка покажет нам сильную запутанность. В этом случае, если первый каон будет круглым, мы будем знать, что второй тоже круглый. А если первый каон квадратный, то таким же будет и второй. Зная форму одного, мы однозначно определим форму другого.

Квантовая версия запутанности выглядит, по сути, также – это отсутствие независимости. В квантовой теории состояния описываются математическими объектами под названием волновая функция. Правила, объединяющие волновые функции с физическими возможностями, порождают очень интересные сложности, которые мы обсудим позже, но основное понятие о запутанном знании, которое мы продемонстрировали для классического случая, остаётся тем же.

Хотя пирожные нельзя считать квантовыми системами, запутанность квантовых систем возникает естественным путём – например, после столкновений частиц. На практике незапутанные (независимые) состояния можно считать редкими исключениями, поскольку при взаимодействии систем между ними возникают корреляции.

Рассмотрим, к примеру, молекулы. Они состоят из подсистем – конкретно, электронов и ядер. Минимальное энергетическое состояние молекулы, в котором она обычно и находится, представляет собой сильно запутанное состояние электронов и ядра, поскольку расположение этих составляющих частиц никак не будет независимым. При движении ядра электрон движется с ним.

Вернёмся к нашему примеру. Если мы запишем Φ■, Φ● как волновые функции, описывающие систему 1 в её квадратных или круглых состояниях и ψ■, ψ● для волновых функций, описывающих систему 2 в её квадратных или круглых состояниях, тогда в нашем рабочем примере все состояния можно описать, как:

Независимые: Φ■ ψ■ + Φ■ ψ● + Φ● ψ■ + Φ● ψ●

Запутанные: Φ■ ψ■ + Φ● ψ●

Независимую версию также можно записать, как:

Отметим, как в последнем случае скобки чётко разделяют первую и вторую системы на независимые части.

Существует множество способов создания запутанных состояний. Один из них – измерить составную систему, дающую вам частичную информацию. Можно узнать, например, что две системы договорились быть одной формы, не зная при этом, какую именно форму они выбрали. Это понятие станет важным чуть позже.

Более характерные последствия квантовой запутанности, такие, как эффекты Эйнштейна-Подольского-Розена (EPR) и Гринберга-Хорна-Зейлингера (GHZ), возникают из-за её взаимодействия ещё с одним свойством квантовой теории под названием «принцип дополнительности». Для обсуждения EPR и GHZ позвольте мне сначала представить вам этот принцип.

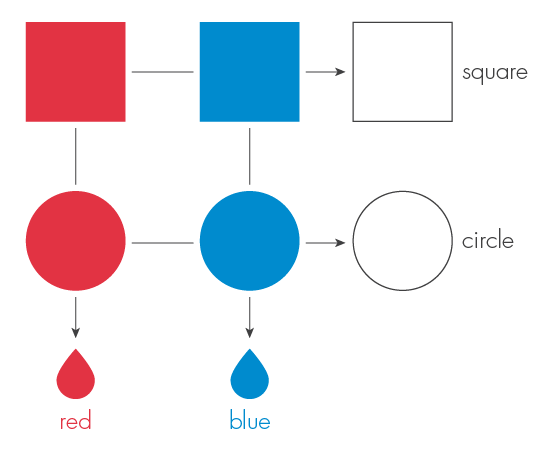
До этого момента мы представляли, что каоны бывают двух форм (квадратные и круглые). Теперь представим, что ещё они бывают двух цветов – красного и синего. Рассматривая классические системы, например, пирожные, это дополнительное свойство означало бы, что каон может существовать в одном из четырёх возможных состояний: красный квадрат, красный круг, синий квадрат и синий круг.

Но квантовые пирожные – квантожные… Или квантоны… Ведут себя совсем по-другому. То, что квантон в каких-то ситуациях может обладать разной формой и цветом не обязательно означает, что он одновременно обладает как формой, так и цветом. Фактически, здравый смысл, которого требовал Эйнштейн от физической реальности, не соответствует экспериментальным фактам, что мы скоро увидим.

Мы можем измерить форму квантона, но при этом мы потеряем всю информацию о его цвете. Или мы можем измерить цвет, но потеряем информацию о его форме. Согласно квантовой теории, мы не можем одновременно измерить и форму и цвет. Ничей взгляд на квантовую реальность не обладает полнотой; приходится принимать во внимание множество разных и взаимоисключающих картин, у каждой из которых есть своё неполное представление о происходящем. Это и есть суть принципа дополнительности, такая, как её сформулировал Нильс Бор.

В результате квантовая теория заставляет нас быть осмотрительными в приписывании свойствам физической реальности. Во избежание противоречий приходится признать, что:

Не существует свойства, если его не измерили.
Измерение – активный процесс, изменяющий измеряемую систему

Теперь опишем две образцовые, но не классические, иллюстрации странностей квантовой теории. Обе были проверены в строгих экспериментах (в реальных экспериментах люди меряют не формы и цвета пирожных, а угловые моменты электронов).

Альберт Эйнштейн, Борис Подольский и Натан Розен (EPR) описали удивительный эффект, возникающий при запутанности двух квантовых систем. EPR-эффект объединяет особую, экспериментально достижимую форму квантовой запутанности с принципом дополнительности.

EPR-пара состоит из двух квантонов, у каждого из которых можно измерить форму или цвет (но не то и другое сразу). Предположим, что у нас есть множество таких пар, все они одинаковые, и мы можем выбирать, какие измерения мы проводим над их компонентами. Если мы измерим форму одного из членов EPR-пары, мы с одинаковой вероятностью получим квадрат или круг. Если измерим цвет, то с одинаковой вероятностью получим красный или синий.

Интересные эффекты, казавшиеся EPR парадоксальными, возникают, когда мы проводим измерения обоих членов пары. Когда мы меряем цвет обоих членов, или их форму, мы обнаруживаем, что результаты всегда совпадают. То есть, если мы обнаружим, что один из них красный и затем меряем цвет второго, мы также обнаруживаем, что он красный – и т.п. С другой стороны, если мы измеряем форму одного и цвет другого, никакой корреляции не наблюдается. То есть, если первый был квадратом, то второй с одинаковой вероятностью может быть синим или красным.

Согласно квантовой теории, мы получим такие результаты, даже если две системы будет разделять огромное расстояние и измерения будут проведены почти одновременно. Выбор типа измерений в одном месте, судя по всему, влияет на состояние системы в другом месте. Это «пугающее дальнодействие», как называл его Эйнштейн, по-видимому, требует передачу информации – в нашем случае, информации о проведённом измерении – со скоростью, превышающей скорость света.

Но так ли это? Пока я не узнаю, какой результат получили вы, я не знаю, чего ожидать мне. Я получаю полезную информацию, когда я узнаю ваш результат, а не когда вы проводите измерение. И любое сообщение, содержащее полученный вами результат, необходимо передать каким-либо физическим способом, медленнее скорости света.

При дальнейшем изучении парадокс ещё больше разрушается. Давайте рассмотрим состояние второй системы, если измерение первой дало красный цвет. Если мы решим мерить цвет второго квантона, мы получим красный. Но по принципу дополнительности, если мы решим измерить его форму, когда он находится в «красном» состоянии, у нас будут равные шансы на получение квадрата или круга. Поэтому, результат EPR логически предопределён. Это просто пересказ принципа дополнительности.

Нет парадокса и в том, что удалённые события коррелируют. Ведь если мы положим одну из двух перчаток из пары в коробки и отправим их в разные концы планеты, неудивительно, что посмотрев в одну коробку, я могу определить, на какую руку предназначена другая перчатка. Точно так же, во всех случаях корреляция пар EPR должна быть зафиксирована на них, когда они находятся рядом и потому они могут выдержать последующее разделение, будто бы имея память. Странность EPR-парадокса не в самой по себе возможности корреляции, а в возможности её сохранения в виде дополнений.

Дэниел Гринбергер, Майкл Хорн и Антон Зейлингер открыли ещё один прекрасный пример квантовой запутанности. ОН включает три наших квантона, находящихся в специально подготовленном запутанном состоянии (GHZ-состоянии). Мы распределяем каждый из них разным удалённым экспериментаторам. Каждый из них выбирает, независимо и случайно, измерять ли цвет или форму и записывает результат. Эксперимент повторяют многократно, но всегда с тремя квантонами в GHZ-состоянии.

Каждый отдельно взятый экспериментатор получает случайные результаты. Измеряя форму квантона, он с равной вероятностью получает квадрат или круг; измеряя цвет квантона, он с равной вероятностью получает красный или синий. Пока всё обыденно.

Но когда экспериментаторы собираются вместе и сравнивают результаты, анализ показывает удивительный результат. Допустим, мы будем называть квадратную форму и красный цвет «добрыми», а круги и синий цвет – «злыми». Экспериментаторы обнаруживают, что если двое из них решили измерить форму, а третий – цвет, тогда либо 0, либо 2 результата измерений получаются «злыми» (т.е. круглыми или синими). Но если все трое решают измерить цвет, то либо 1 либо 3 измерения получаются злыми. Это предсказывает квантовая механика, и именно это и происходит.

Вопрос: количество зла чётное или нечётное? В разных измерениях реализовываются обе возможности. Нам приходится отказаться от этого вопроса. Не имеет смысла рассуждать о количестве зла в системе без связи с тем, как его измеряют. И это приводит к противоречиям.

Эффект GHZ, как описывает его физик Сидни Колман, это «оплеуха от квантовой механики». Он разрушает привычное, полученное из опыта ожидание того, что у физических систем есть предопределённые свойства, независимые от их измерения. Если бы это было так, то баланс доброго и злого не зависел бы от выбора типов измерений. После того, как вы примете существование GHZ-эффекта, вы его не забудете, а ваш кругозор будет расширен.

Пока что мы рассуждаем о том, как запутанность не позволяет назначить уникальные независимые состояния нескольким квантонам. Такие же рассуждения применимы к изменениям одного квантона, происходящим со временем.

Мы говорим об «запутанных историях», когда системе невозможно присвоить определённое состояние в каждый момент времени. Так же, как в традиционной запутанности мы исключаем какие-то возможности, мы можем создать и запутанные истории, проводя измерения, собирающие частичную информацию о прошлых событиях. В простейших запутанных историях у нас есть один квантон, изучаемый нами в два разных момента времени. Мы можем представить ситуацию, когда мы определяем, что форма нашего квантона оба раза была квадратной, или круглой оба раза, но при этом остаются возможными обе ситуации. Это темпоральная квантовая аналогия простейшим вариантам запутанности, описанным ранее.

Используя более сложный протокол, мы можем добавить чуть-чуть дополнительности в эту систему, и описать ситуации, вызывающие «многомировое» свойство квантовой теории. Наш квантон можно подготовить в красном состоянии, а затем измерить и получить голубое. И как в предыдущих примерах, мы не можем на постоянной основе присвоить квантону свойство цвета в промежутке между двумя измерениями; нет у него и определённой формы. Такие истории реализовывают, ограниченным, но полностью контролируемым и точным способом, интуицию, свойственную картинке множественности миров в квантовой механике. Определённое состояние может разделиться на две противоречащие друг другу исторические траектории, которые затем снова соединяются.

Эрвин Шрёдингер, основатель квантовой теории, скептически относившийся к её правильности, подчёркивал, что эволюция квантовых систем естественным образом приводит к состояниям, измерение которых может дать чрезвычайно разные результаты. Его мысленный эксперимент с «котом Шрёдингера» постулирует, как известно, квантовую неопределённость, выведенную на уровень влияния на смертность кошачьих. До измерения коту невозможно присвоить свойство жизни (или смерти). Оба, или ни одно из них, существуют вместе в потустороннем мире возможностей.

Повседневный язык плохо приспособлен для объяснения квантовой дополнительности, в частности потому, что повседневный опыт её не включает. Практические кошки взаимодействуют с окружающими молекулами воздуха, и другими предметами, совершенно по-разному, в зависимости от того, живы они или мертвы, поэтому на практике измерение проходит автоматически, и кот продолжает жить (или не жить). Но истории с запутанностью описывают квантоны, являющиеся котятами Шрёдингера. Их полное описание требует, чтобы мы принимали к рассмотрению две взаимоисключающие траектории свойств.

Контролируемая экспериментальная реализация запутанных историй – вещь деликатная, поскольку требует сбора частичной информации о квантонах. Обычные квантовые измерения обычно собирают всю информацию сразу – к примеру, определяют точную форму или точный цвет – вместо того, чтобы несколько раз получить частичную информацию. Но это можно сделать, хотя и с чрезвычайными техническими трудностями. Этим способом мы можем присвоить определённый математический и экспериментальный смысл распространению концепции «множественности миров» в квантовой теории, и продемонстрировать её реальность.

Содержание

Pелятивистская квантовая механика. Уравнение Дирака
А все началось с игры
Теория, порождающая загадки
Тату уравнение дирака квантовая запутанность
📸 Видео

Видео:Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

Pелятивистская квантовая механика. Уравнение Дирака

«На нем стоит большая часть физики и вся химия.»
Поль Дирак о своем уравнении

Вся классическая физика зиждется на том убеждении, что, зная закон движения частицы и факт появления ее в точке А, мы абсолютно точно можем предсказать, когда она попадет в точку В. Квантовая механика утверждает, что, зная закон движения микрочастицы и факт появления ее в точке А, мы можем определить всего лишь вероятность ее появления в точке В.

Вначале объясним слово «релятивистский». В физике под этим термином понимают все связанное с теорией относительности применительно к физическим эффектам, явлениям, наблюдаемым при скоростях тел или частиц, сравнимых со скоростью света. Так, к примеру, релятивистская частица—это частица, движущаяся с релятивистской скоростью, то есть близкой к скорости света.

Видео:Квантовая формула любвиСкачать

А все началось с игры

В 1928 году английский физик Поль Дирак вывел уравнение движения для классического поля электрона, являющегося релятивистской частицей. Позднее оно было применено и для описания других фермионов. Однако по порядку.

Сам Дирак вспоминал, что начал работать над своей релятивистской теорией, «играясь с уравнениями, а не пытаясь ввести какую-нибудь определенную физическую идею». В чем же состояла эта игра Дирака?

Он хотел найти такое уравнение, которое, во-первых, было бы релятивистским, то есть удовлетворяло принципам теории относительности, во-вторых, подчинялось бы требованиям теории преобразований и, в-третьих, было бы квантово-механическим уравнением, описывающим движение электрона.

Но что значит «релятивистское уравнение»? Одним из характерных признаков такого уравнения является то, что в него должны входить как пространственные координаты х, у, z, так и временная координата t. Это уравнение должно быть квантово-механическим, то есть содержать волновую функцию электрона.

Дирак хотел просто привести в соответствие релятивистские принципы и требования теории преобразований. Оказалось, что существование спина как бы само собой возникает при объединении квантовой механики и теории относительности. Получилось, что квантовое уравнение, записанное с учетом требований теории относительности, описывает поведение частиц со спином.

Дираковская теория электрона наделяет электрон релятивистскими свойствами, а именно спином, то есть собственным механическим моментом количества движения и собственным магнитным моментом.

Релятивистский — термин, употребляемый в физике для явлений, обусловленных движением со скоростями, близкими к скорости света, либо сильными полями тяготения. Такие явления описываются теорией относительности.

Видео:▽ Квантовая запутанность(что такое квантовая запутанность)Скачать

Теория, порождающая загадки

Уравнение Дирака дало возможность получить более точную формулу для уровней энергии атома водорода. Но особенностью его уравнения было наличие среди его решений таких, которые соответствуют состояниям с отрицательными значениями энергии для свободного движения частицы, а это уже соответствует отрицательной массе частицы. Это означало, что все механические законы для частицы в таких состояниях были бы неверными, переходы же в квантовой теории в эти состояния возможны. Действительный физический смысл переходов на уровни с отрицательной энергией выяснился, когда была доказана возможность взаимопревращения частиц. Из уравнения Дирака следовало, что должна существовать новая частица—античастица по отношению к электрону, с массой электрона и зарядом противоположного знака. Такая частица была открыта в 1932 году американским физиком-экспериментатором Карлом Андерсоном и получила название «позитрон». Переход электрона из состояния с отрицательной энергией в состояние с положительной энергией и обратный переход рассматриваются как процесс образования пары электрон — позитрон и аннигиляция, то есть взаимное уничтожение такой пары.

Однако, несмотря на эти успехи, теория Дирака имеет и недостаток. Она не описывает взаимодействие квантованного электронного поля с квантованным электромагнитным полем, в том числе и рождение или уничтожение частиц. Эта трудность была разрешена в квантовой теории поля. В случае с электронами следует добавить квантованное электромагнитное поле, квантование самого электронного поля и взаимодействие этих полей, а полученная теория уже называется квантовой электродинамикой.

«. Квантовую электродинамику можно уложить в рамки разумной математической теории, но лишь ценой нарушения релятивистской инвариантности. Мне, однако, это кажется меньшим злом, чем отступление от стандартных правил математики и пренебрежение бесконечными величинами» (Поль Дирак)

Видео:Парфёнов К. В. - - Квантовая теория - Уравнение Дирака. Спиноры (Лекция 2)Скачать

Тату уравнение дирака квантовая запутанность

применимо для описания частиц, скорость которых меньше скорости света c. Оно не удовлетворяет принципам специальной теории относительности, т.к. не инвариантно относительно преобразований Лоренца. В уравнение Шредингера координаты и время входят неравноправно – оно содержит первую производную по времени и вторые производные по координатам.
Релятивистская механика основана на соотношении

E 2 = c 2 p 2 + m 2 c 4 ,

(2.1)

связывающем энергию и импульс частицы. Для получения релятивистского уравнения можно поступить так же, как в нерелятивистском случае уравнения Шредингера. Для получения волнового уравнения в соотношении (2.1) от классических величин энергии E и импульса p нужно перейти, так же как в уравнении Шредингера, к операторам

и подействовать на волновую функцию ψ.
Релятивистское волновое уравнение было получено независимо Клейном, Гордоном и Фоком и носит их имя

Состояние частицы зависит от трёх координат и времени ψ(x,y,z,t). Уравнение Клейна–Гордона–Фока представляет собой волновое уравнение второго порядка. Оно описывает динамику релятивистской квантовой системы. Так как уравнение Клейна–Гордона–Фока является уравнением второго порядка, для его решения в начальный момент времени необходимо задать значение не только волновой функции ψ, но и её первой производной. Оказалось, что для уравнения Клейна–Гордона–Фока нельзя ввести положительно определённую плотность вероятности ψ*ψ. Уравнение Клейна–Гордона–Фока описывает состояние частиц с нулевым значением спина. Однако уже к тому времени, когда П. Дирак работал над релятивистской теорией электрона (1925 г.), было известно, что электрон имеет спин s = 1/2. Спин электрона был введён в 1925 г. Дж. Уленбеком и С. Гоудсмитом для объяснения дублетной структуры одноэлектронных уровней.
Принцип суперпозиции требует, чтобы релятивистское волновое уравнение было линейным. На основании этих принципов П. Дирак сформулировал релятивистски-инвариантное уравнение, записав его в виде

Тату уравнение дирака квантовая запутанность

(2.2)

Соотношение представляет собой наиболее общую линейную форму, содержащую первые производные от волновой функции ψ. В уравнение (2.2) координаты и время входят равноправно и не содержат вторых производных. Для нахождения величин α_x, α_y, α_z, β уравнение (2.2) можно записать в виде

(2.3)

имеющем формальное сходство с уравнением Шредингера. Если оператор представляет собой оператор Гамильтона, то между оператором и операторами импульса должна быть такая же связь как между энергией и импульсом в специальной теории относительности

(2.4)

Используя соотношение (2.4), можно определить неизвестные коэффициенты α_x, α_y, α_z, β. Возведя оператор в квадрат, получим

Оператор 2 будет иметь вид (2.4), если величины α_x, α_y, α_z, β будут удовлетворять следующим условиям.

α_iα_k + α_kα_i = 0, α ≠ k,
α_iβ = βα_i = 0,
i = x,y,z.

(2.5)

Очевидно, что обычные числа не могут удовлетворять условиям (2.5), т.к. для них не выполняются условия антикоммутации. Для обычных чисел выполняются условия коммутации α_iα_k + α_kα_i = 0. Дирак предположил, что условиям коммутации (2.5) удовлетворяют матрицы 4 порядка, составленные из матриц Паули.

(2.6)

Умножая матрицы (2.6) друг на друга можно убедиться, что они удовлетворяют условиям (2.5).
Используя матрицы Паули σ_x, σ_y, σ_z, матрицы α_x, α_y, α_z, β можно записать в виде

С помощью операторов _x, _y, _z, уравнение (2.2) приводится к виду

Это уравнение называется уравнение Дирака для свободной частицы. Если ввести векторный оператор , то уравнение Дирака можно записать в более компактном виде

Так как на волновую функцию ψ(x,y,z,t) действуют матрицы 4×4, волновая функция ψ(x,y,z,t) также должна быть четырехкомпонентной.

Матричное волновое уравнение Дирака эквивалентно системе четырех связанных между собой уравнений

Четырехкомпонентную волновую функцию электрона можно представить как 4 различных комбинации положительной и отрицательной энергий электрона и двух значений проекции спина электрона σ_z = 1/2 и σ_z = -1/2.

П. Дирак: «Коль скоро я взялся оценивать других физиков, нельзя не сказать о Шрёдингере. Мне кажется, что я никогда не видел его в Копенгагене, во всяком случае, я этого не припомню. Но мы немало встречались потом, и из всех знакомых физиков Шрёдингер был, наверное, больше других похож на меня. Я обнаружил, что с Шрёдингером я соглашался гораздо легче, чем с кем-нибудь другим. Дело, наверное, было в том, что мы оба очень ценили математическую красоту и воплощение этой красоты в нашей работе. Для нас было символом веры то, что все уравнения, описывающие фундаментальные законы Природы, должны отличаться математической красотой. Это было для нас почти религией, причем очень полезной, ибо ее можно считать основой многих наших успехов.
Когда вы читаете о работах Шрёдингера. вас может удивить одно обстоятельство. Шрёдингер пришел к квантовой механике через волновое уравнение де Бройля, которое было релятивистским. Шрёдингер находился под большим впечатлением красоты релятивистской теории относительности, и возникает вопрос, почему так случилось, что работа Шрёдингера, где он вводит волновое уравнение, написана в нерелятивистском духе. Здесь кроется какое-то противоречие.
Много лет спустя, не помню точно, но примерно году в 1940‑м, близко познакомившись с Шрёдингером, я узнал от него, в чем было дело. Он рассказал, что работал тогда в релятивистском подходе, навеянном работами де Бройля, и, вводя электромагнитные потенциалы, пришел к релятивистскому волновому уравнению, которое оказалось обобщением уравнения де Бройля. Первый его порыв быт посмотреть, что получится, если с помощью этого уравнения рассчитать атом водорода. Произведя расчеты, Шрёдингер обнаружил, что результаты не согласуются с опытом.
Он был сильно разочарован и, решив, что его волновое уравнение никуда не годится, отказался от него. Взглянув на это уравнение по-новому через несколько месяцев, Шрёдингер заметил, что если понизить точность и перейти к нерелятивистскому приближению, то результаты согласуются с экспериментальными данными, конечно, в пренебрежении релятивистскими эффектами. Таким образом, волновое уравнение Шрёдингера в нерелятивистском виде согласовывалось с экспериментом, и его можно было публиковать.
Причиной того, что первоначальное, релятивистское уравнение Шрёдингера не согласовывалось с экспериментом, был, конечно, неучтенный спин электрона. Мысль о том, что у электрона есть спин, была тогда совершенно новой, и Шрёдингер мог о ней даже не слышать, а в то время у него не хватало смелости публиковать уравнение, которое давало результат, наверняка противоречащий эксперименту [*] ».

Решение уравнения Дирака для свободной частицы показывает, что каждому значению импульса p соответствуют два значение энергии E

E = ±(m 2 c 4 + c 2 p 2 ) 1/2 ,

т.е. энергия частицы может принимать два значения, как положительное, так и отрицательное. В классической физике все величины изменяются непрерывно, поэтому без потери общности отрицательные значения энергии можно было отбросить, т.к. положительные и отрицательные области энергии разделены энергетическим интервалом 2mc 2 и непрерывный переход частицы из одной области в другую невозможен. Однако в релятивистской квантовой теории возможны квантовые переходы из состояний с отрицательной энергией в состояния с положительной энергией и обратно. Поэтому отрицательные значения энергии отбросить нельзя. Возникла проблема − как интерпретировать состояния электрона с отрицательной энергией? Какой физический смысл имеют состояния с отрицательной энергией? Рассмотрим ситуацию, когда частица с положительной энергией E₀ > 0 переходит из точки А в точку В.

Тогда в точке А величина энергии E уменьшается на величину E₀, а в точке В увеличивается на величину E₀. Для частицы с отрицательной энергией E₀ отрицательной энергией — E и зарядом -q из состояния В в состояние А. С остояния с отрицательной энергией приводят к появлению у каждой частицы двойника, который имеет положительную энергию и противоположный электрический заряд.
Таким образом, согласно теории Дирака, заряженная частицы должна иметь двойника с противоположным зарядом и такой же массой. Например, у электрона должен быть двойник, имеющий такую же массу, как электрон, но положительный электрический заряд.

На «языке» квантовой физики волновую функцию частицы с положительной энергией E + = E > 0, движущейся в положительном направлении вдоль оси х, записывают в виде

В случае постоянной фазы волны

т.е. частица с положительной энергией движется вправо вдоль оси x. Для состояния с отрицательной энергией E — (E — |.
Частица с отрицательной энергией ведёт себя, как частица с положительной энергией, но движущаяся «назад по времени». Другой пример движения «назад по времени» − поведение частицы с отрицательным зарядом -q, движущейся в постоянном магнитном поле. Движение частицы описывается уравнением Лоренца

т.е. движение частицы с положительным зарядом +q описывается тем же уравнением, что и частицы с отрицательным зарядом. Но частица с положительным зарядом в этом случае движется назад по времени − вращается в противоположном направлении в магнитном поле.
Из рассмотренных примеров видно, что частица, имеющая электрический заряд +q и отрицательную энергию, ведёт себя так же как и частица с отрицательным электрическим зарядом -q и положительной энергией.
Электрон с отрицательной энергией должен двигаться во внешнем поле как частица с положительным зарядом. Поэтому при переходе электрона области положительных энергий в область отрицательных энергий должен одновременно измениться заряд электрона – он должен стать положительным +e. Переходы электронов в состояния с отрицательной энергией нарушали закон сохранения электрического заряда. Нужно было найти способ запретить такие переходы. Ход мыслей П. Дирака был следующий. Так как электроны являются фермионами, это можно было сделать, предположив, что все состояния с отрицательной энергией заняты. Тогда в соответствии с принципом Паули переходы в состояния с отрицательной энергией оказываются запрещёнными. Однако такое предположение приводило к новой проблеме − бесконечному числу частиц, заполняющих все отрицательные состояния − появлению физического вакуума, имеющего бесконечный электрический заряд и массу. Возможность такого состояния Дирак объяснил тем, что бесконечный физический вакуум будет ненаблюдаем, так как наблюдаются только отклонения энергии или электрического заряда от состояния физического вакуума. Можно ли обнаружить электроны заполняющие отрицательные состояния физического вакуума? Гамма-квант с энергией большей, чем 2m_ec 2 может перевести электрон из состояния с отрицательной энергией в состояние с положительной энергией. Тогда будет наблюдаться обычный электрон с положительной энергией и отрицательным зарядом, а вакантное место в вакууме будет наблюдаться как частица с положительным зарядом. Так как в то время была известна всего одна частица с положительным электрическим зарядом – протон, Дирак первоначально отождествил протоны с частицами, заполняющими отрицательные состояния вакуума. Однако это предположение породило новые, гораздо более сложные проблемы − неустойчивость нашего мира − приводило к невозможности существования атома водорода. Электрон и протон должны были в результате взаимодействия исчезнуть, превратившись в γ-кванты. Кроме того, необходимо было объяснить большую разницу масса электрона и протона. Если протон это действительно дырка, образовавшаяся в результате вылета электрона, почему протон имеет массу в 2000 раз больше массы электрона? Дирак верил в созданную им теорию дырок и в результате сделал следующий шаг. Он объявил, что должна существовать новая неизвестная частица, имеющая такую же массу как электрон, но положительный электрический заряд. Эта частица является античастицей по отношению к электрону.

П. Дирак: «На протяжении двух лет я занимался боровскими орбитами и пришел к выводу, что развить их в общую квантовую механику безнадежно. В это время Гейзенберг предложил свою матричную механику, и мне вдруг стало ясно, что ключом к решению проблемы служит некоммутативная алгебра. Вскоре Шредингер разработал волновую механику и показал, что она эквивалентна теории Гейзенберга.
Основываясь на этих теориях, я развил общую теорию преобразований, которую можно было применять при вычислении вероятностей любых коммутирующих динамических переменных. Это доставило мне большое удовлетворение.
Для построения релятивистской теории частицы имелось волновое уравнение Клейна − Гордона, квадратичное по ∂/∂t . В то время оно удовлетворяло большинство физиков. Мне же оно не нравилось, потому что я был очень привязан к своей теории преобразований, которая требовала, чтобы уравнение было линейным по ∂/∂t . Эта неудовлетворенность заставила меня продолжить поиски нового релятивистского волнового уравнения. Наконец, я нашел уравнение, линейное по ∂/∂t и совместимое с моей теорией преобразований. Оно автоматически привело к спину h/2 и к правильному значению магнитного момента электрона. Эти результаты были неожиданными для меня.
Я применил это уравнение к электрону в атоме водорода в первом приближении теории возмущений и получил результаты, согласующиеся с данными опыта. Уравнение автоматически приводило к правильному магнитному .моменту, и именно поэтому оно не содержало той ошибки, которая получалась при использовании уравнения Клейна − Гордона, приводившего к неверным результатам для спектра водорода.
Но у этого уравнения имелась и новая трудность, а именно, частица могла находиться в состояниях с отрицательной энергией. Я знал о такой трудности с проблемой отрицательных энергий с самого начала работы, но считал это затруднение менее серьезным по сравнению с остальными, не столь серьезным, как, например, невозможность применять преобразования, вытекающие из общей теории преобразований.
Проблема отрицательных энергий была разрешена несколько позже выдвинутой мною идеей об учете принципа исключения Паули для электронов (согласно которому в любом данном состоянии не может находиться более одного электрона) при дополнительном смелом предположении, что все состояния с отрицательной энергией в вакууме заполнены, а потому дырка в состояниях с отрицательной энергией проявляется как физическая частица. Это была бы частица со спином электрона, но она обладала бы положительным зарядом вместо отрицательного заряда у электрона и имела бы положительную энергию.
Когда я впервые обдумывал эту идею, я считал, что новая частица должна иметь такую же массу, что и электрон, вследствие симметрии между положительными и отрицательными массами и энергиями, которая всюду проявляется в теории. Но в те времена единственными известными элементарными частицами были электрон и протон. Я не осмелился постулировать существование новой частицы. Весь климат общественного мнения в те дни был против постулирования новых частиц, в резком контрасте с тем, что мы наблюдаем сейчас. Тогда я опубликовал свою работу как теорию электронов и протонов в надежде, что каким-то необъяснимым образом кулоновское взаимодействие между частицами приведет к большому отличию в массах электрона и протона.
Конечно, в этом пункте я был совершенно неправ и вскоре математики указали, что абсолютно невозможно получить такую асимметрию между состояниями с положительной и отрицательной энергиями. И впервые Вейль опубликовал категорическое утверждение о том, что новая частица должна иметь такую же массу, что и электрон. Теория с равными массами была подтверждена немного спустя на опыте, когда Андерсон обнаружил позитрон».

Частица с зарядом +q является античастицей по отношению к частице с зарядом -q. Аналогичные рассуждения относятся к частице с отрицательным зарядом. Частицы с отрицательной энергией являются античастицами по отношению к частицам с положительной энергией.
Наряду с электроном, имеющим отрицательный электрический заряд, должна, согласно уравнению Дирака, существовать положительно заряженная античастица.
Античастицы должны существовать не только у электрически заряженных частиц, но и у частиц, имеющих сохраняющуюся в различных физических процессах физическую величину. Одним из таких квантовых чисел является барионное число (заряд) B. Поэтому нейтрон, имеющий электрический заряд Q = 0, но единичный положительный барионный заряд, тоже должен иметь античастицу – антинейтрон.

B(n) = +1, Q(n) = 0; B() = -1, Q() = 0

Античастицей протона является частица, имеющая такую же массу как протон, равный по абсолютной величине, но отрицательный электрический заряд. Барионные заряды протона и антипротона также имеют противоположные значения

B(p) = +1, Q(p) = +1e; B() = -1, Q() = -1e

С современной точки зрения в большинстве случаев нет необходимости рассматривать античастицы как частицы, распространяющиеся назад во времени. Гораздо проще рассматривать частицы и античастицы как физические объекты, характеризующиеся определённым набором квантовых чисел. Какие-то квантовые числа у частицы и античастицы совпадают, а какие-то имеют противоположные значения. Существенно то, что

частица и античастица при взаимодействии аннигилируют,
из состояния с нулевыми квантовыми числами частица и античастица всегда рождаются парами.

Поэтому в дальнейшем на диаграммах Фейнмана мы не будем рисовать стрелки, а рядом с внешними и внутренними линиями в тех случаях, когда это необходимо, будем указывать тип частицы.

[*] Dirас P. А . М . Recollections of an Exciting Era//History of Twentieth Century Physics: Proceedings of the International [Summer] School of Physics «Enrico Fermi». Course LVII. Varenna, Lake Como, Italy, villa Monastero. July 31 — August 12. 1972,- (Rendiconti S. I. F. — LVII).- New York: Academic Press, 1977 — P. 109-146.- УФН, том 153, вып. 1 (1987). Перевод H. Я. Смородинской.