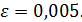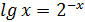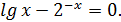Тема: Табулирование функции. Применение табулирования к решению уравнения f(x)=0.
Цель работы: составление программы табулирования функции y= f(x) и ее использование для нахождения корня уравнения f(x)=0 с заданной точностью.
Варианты заданий лабораторной работы №3 приведены в таблице 3.1.
Работа состоит из двух задач:
Задача 1. Найти таблицу значений функций y = f(x) на отрезке [a, b] с шагом h.
Задача 2.Вычислить корень уравнения f(x) = 0 на отрезке [a, b] с точностью e=0,005.
Перед выполнением задания любого уровня необходимо проверить графически, что на заданном отрезке [a, b] находится корень уравнения. Если корня на заданном отрезке нет, то следует определить по графику новый отрезок, содержащий корень, и при решении задачи рассматривать его. График привести в отчёте.
Задание (1 уровень)
1. Графически получить приближённое решение уравнения f(x) = 0. Уравнение взять из таблицы 3.1 в соответствии с номером своего варианта.
2. Составить блок-схему алгоритма табулирования функции f(x) на отрезке [a, b] с шагом h=0,1.
3. Составить программу табулирования функции f(x) на отрезке [a, b] с шагом h=0,1.
4. Ввести программу, выполнить её, получить и выписать 11 пар значений (x, y).
5. Для вычисления корня уравнения f(x) = 0 найти и выписать отрезок 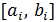
6. Повторно запуская программу табулирования, получить таблицу значений функции f(x) на отрезке 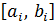
7. С экрана выписать новый отрезок 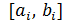
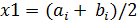
8. Вычислить значение функции в корне. Выписать полученные результаты.
Задание (2 уровень)
1. Графически получить приближенное решение уравнения f(x) = 0. Уравнение взять из таблицы 3.1 в соответствии с номером своего варианта.
2. Изменить блок-схему задачи табулирования функции f(x), предусмотрев возможность повторного запуска алгоритма табулирования на новом интервале с новым шагом h ( 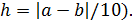
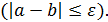
3. Составить программу табулирования f(x) на [a, b] с шагом h по новой блок-схеме.
4. Запустить программу, получить результаты по табулированию функции f(x) последовательно на данном интервале [a, b] с шагом h=0,1 и на каждом новом интервале 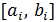
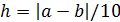
5. С экрана выписать результаты табулирования на первом интервале, а для последующих результатов – выписывать две строки, где функция меняет свой знак. Выписать корень уравнения и значение функции в корне.
Задание (3 уровень)
1. Графически получить приближённое решение уравнения f(x) = 0. Уравнение взять из таблицы 3.1 в соответствии с номером своего варианта.
2. Составить блок-схему и программу, реализующие алгоритм вычисления корня уравнения f(x)=0 на интервале [a, b] с заданной точностью 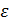
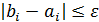
Замечания:
а) на каждом отрезке 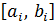
б) приближенным решением уравнения считать середину последнего отрезка 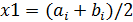
3. Ввести программу, выполнить её и получить результат. На экран вывести границы каждого нового интервала поиска корня, корень уравнения, заданную точность и значение функции в корне.
Задача 1. Найти таблицу значений функций y= f(x) на отрезке [a, b] с шагом h=0.1, где 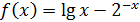
Задача 2.Найти корень уравнения f(x) = 0 на отрезке [a, b] с точностью
e= 0.005.
Порядок выполнения задания (1 уровень)
1. Решение уравнения графическим методом.
1.1. Проверим графически, что на заданном отрезке [a, b] есть корень уравнения f(x)= 0, т.е.
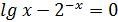
Перепишем уравнение (1):
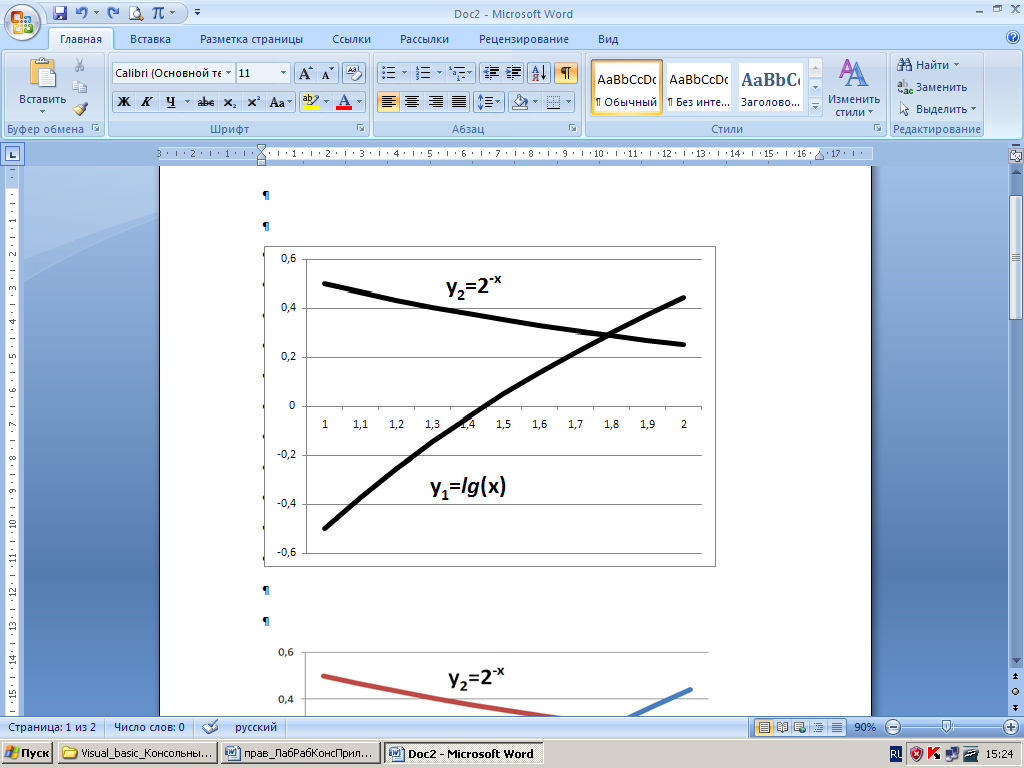
Построим два графика 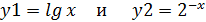
| M |
| X * |
Рис. 3.1. Пересечение графиков
Графики пересекаются друг с другом в точке М. Абсцисса точки М (X * ) – есть корень уравнения
1.2. Если на заданном в условии отрезке графики не пересекаются, то это означает, что данный отрезок не содержит корня уравнения. В этом случае следует определить по графику новый отрезок, содержащий корень, и при решении задачи рассматривать его.
2. Составление блок-схемы задачи табулирования.
2.1. Входные данные: a, b – границы отрезка, h — шаг.
Выходные данные: 11 пар значений (x, y).
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAUwHCU8IA AADaAAAADwAAAGRycy9kb3ducmV2LnhtbESPQYvCMBSE7wv7H8Jb8LKsqSKydI1SCqIHYdHV+6N5 tsXkpSTR1n9vhAWPw8x8wyxWgzXiRj60jhVMxhkI4srplmsFx7/11zeIEJE1Gsek4E4BVsv3twXm 2vW8p9sh1iJBOOSooImxy6UMVUMWw9h1xMk7O28xJulrqT32CW6NnGbZXFpsOS002FHZUHU5XK2C 350pvSmp35T30/Z4mhWfu3mh1OhjKH5ARBriK/zf3moFM3heSTdALh8AAAD//wMAUEsBAi0AFAAG AAgAAAAhAPD3irv9AAAA4gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQ SwECLQAUAAYACAAAACEAMd1fYdIAAACPAQAACwAAAAAAAAAAAAAAAAAuAQAAX3JlbHMvLnJlbHNQ SwECLQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEAAAAAAAAAAAAAAAAAApAgAAZHJzL3NoYXBleG1s LnhtbFBLAQItABQABgAIAAAAIQBTAcJTwgAAANoAAAAPAAAAAAAAAAAAAAAAAJgCAABkcnMvZG93 bnJldi54bWxQSwUGAAAAAAQABAD1AAAAhwMAAAAA «>
| начало |
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAZsxCcMIA AADaAAAADwAAAGRycy9kb3ducmV2LnhtbESPT4vCMBTE7wt+h/AEb2uq4LJWo6hQ8SLL+gevj+a1 KTYvpYlav/1mQfA4zMxvmPmys7W4U+srxwpGwwQEce50xaWC0zH7/AbhA7LG2jEpeJKH5aL3McdU uwf/0v0QShEh7FNUYEJoUil9bsiiH7qGOHqFay2GKNtS6hYfEW5rOU6SL2mx4rhgsKGNofx6uFkF m/WlzM7Nz37bmUudVfsim04KpQb9bjUDEagL7/CrvdMKJvB/Jd4AufgDAAD//wMAUEsBAi0AFAAG AAgAAAAhAPD3irv9AAAA4gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQ SwECLQAUAAYACAAAACEAMd1fYdIAAACPAQAACwAAAAAAAAAAAAAAAAAuAQAAX3JlbHMvLnJlbHNQ SwECLQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEAAAAAAAAAAAAAAAAAApAgAAZHJzL3NoYXBleG1s LnhtbFBLAQItABQABgAIAAAAIQBmzEJwwgAAANoAAAAPAAAAAAAAAAAAAAAAAJgCAABkcnMvZG93 bnJldi54bWxQSwUGAAAAAAQABAD1AAAAhwMAAAAA «>
| a, b, h |
| x= a,b,h |
| y=f(x) |
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAQCjn8sQA AADbAAAADwAAAGRycy9kb3ducmV2LnhtbESPQWvCQBSE70L/w/IK3nRTpa1GV6lCpBcRreL1kX3J BrNvQ3bV9N93C4LHYWa+YebLztbiRq2vHCt4GyYgiHOnKy4VHH+ywQSED8gaa8ek4Jc8LBcvvTmm 2t15T7dDKEWEsE9RgQmhSaX0uSGLfuga4ugVrrUYomxLqVu8R7it5ShJPqTFiuOCwYbWhvLL4WoV rFfnMjs1u+2mM+c6q7ZFNn0vlOq/dl8zEIG68Aw/2t9awfgT/r/EHyAXfwAAAP//AwBQSwECLQAU AAYACAAAACEA8PeKu/0AAADiAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnht bFBLAQItABQABgAIAAAAIQAx3V9h0gAAAI8BAAALAAAAAAAAAAAAAAAAAC4BAABfcmVscy8ucmVs c1BLAQItABQABgAIAAAAIQAzLwWeQQAAADkAAAAQAAAAAAAAAAAAAAAAACkCAABkcnMvc2hhcGV4 bWwueG1sUEsBAi0AFAAGAAgAAAAhAEAo5/LEAAAA2wAAAA8AAAAAAAAAAAAAAAAAmAIAAGRycy9k b3ducmV2LnhtbFBLBQYAAAAABAAEAPUAAACJAwAAAAA= «>
| a, b, h |
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAWip1C8AA AADbAAAADwAAAGRycy9kb3ducmV2LnhtbERPy4rCMBTdD/gP4QpuBk11BpFqlFIYdCEM42N/aa5t MbkpScbWvzeLgVkeznuzG6wRD/KhdaxgPstAEFdOt1wruJy/pisQISJrNI5JwZMC7Lajtw3m2vX8 Q49TrEUK4ZCjgibGLpcyVA1ZDDPXESfu5rzFmKCvpfbYp3Br5CLLltJiy6mhwY7Khqr76dcq+D6a 0puS+n35vB4u18/i/bgslJqMh2INItIQ/8V/7oNW8JHGpi/pB8jtCwAA//8DAFBLAQItABQABgAI AAAAIQDw94q7/QAAAOIBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1sUEsB Ai0AFAAGAAgAAAAhADHdX2HSAAAAjwEAAAsAAAAAAAAAAAAAAAAALgEAAF9yZWxzLy5yZWxzUEsB Ai0AFAAGAAgAAAAhADMvBZ5BAAAAOQAAABAAAAAAAAAAAAAAAAAAKQIAAGRycy9zaGFwZXhtbC54 bWxQSwECLQAUAAYACAAAACEAWip1C8AAAADbAAAADwAAAAAAAAAAAAAAAACYAgAAZHJzL2Rvd25y ZXYueG1sUEsFBgAAAAAEAAQA9QAAAIUDAAAAAA== «>
| конец |
2.2. Блок – схема (рис. 3.2):
Рис. 3.2. Блок-схема алгоритма табулирования
3. Составление программы по блок-схеме из п.2.
3.1. Объявить переменные A, B, H, Y, X одинарной точности вещественного типа (Single).
3.2. Запросить ввод исходных данных с клавиатуры (Console.WriteLine()).
3.3. Открыть цикл для вычисления значения функции Y для аргумента X, изменяющегося от A до B с шагом H (For X = A To В Step H).
3.4. В цикле вычислить и вывести на экран значение функции Y(X) и соответствующего аргумента X.
3.5. Закрыть цикл (Next X) и завершить программу.
4. Выполнить программу и выписать результаты в отчёт (по аналогии с рис. 3.3).
| x = 1 | y = — 0.5 | x = 1.6 | y = — 0.126 |
| x = 1.1 | y = — 0.425 | x = 1.7 | y = — 0.77 |
| x = 1.2 | y = — 0.356 | x = 1.8 | y = — 0.032 |
| x = 1.3 | y = — 0.292 | x = 1.9 | y = 1.08 E-02 |
| x = 1.4 | y = — 0.232 | x = 2 | y = 5.10 E-02 |
| x = 1.5 | y = — 0.177 |
Рис. 3.3. Результаты: 11 пар значений (x, y)
5. Из таблицы значений, полученной в п.4, найти и выписать отрезок, на котором функция f(x) меняет свой знак. В данном случае это отрезок [1.8, 1.9], т.к. f(1.8) 0.
6. На найденном отрезке [1.8, 1.9] запустить программу табулирования функции f(x) с шагом h =0.01.
7. Из полученных результатов найти и выписать две строки, где функция f(x) меняет знак:
x = 1.87 y = — 1.732Е-08 f(x) 0
8. Вычислить середину выбранного отрезка [1.87, 1.88]: X1=(1.87+1.88)/2 = 1.875 и значение функции в корне X1 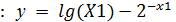
9. Выписать результаты: значение корня (X1), значение функции в корне (y(X1)).
Вывод: значение X1=1.875 является приближённым значением корня уравнения с точностью 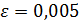
Дата добавления: 2014-12-09 ; просмотров: 3691 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Как найти корни уравнения в Excel с помощью Подбора параметраСкачать

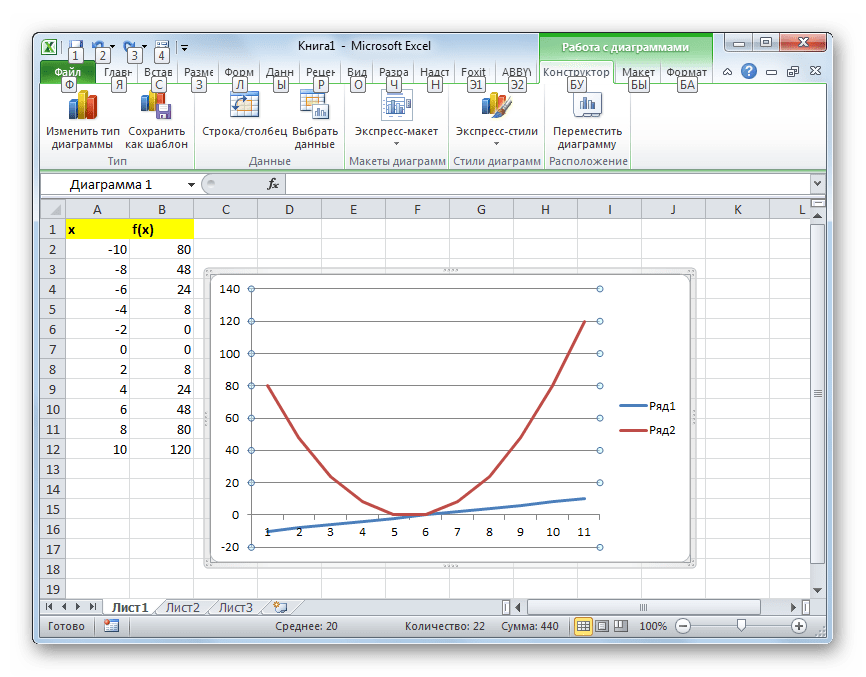
Применение табулирования функции в Microsoft Excel
Табулирование функции представляет собой вычисление значения функции для каждого соответствующего аргумента, заданного с определенным шагом, в четко установленных границах. Эта процедура является инструментом для решения целого ряда задач. С её помощью можно локализовать корни уравнения, найти максимумы и минимумы, решать другие задачи. С помощью программы Excel выполнять табулирование намного проще, чем используя бумагу, ручку и калькулятор. Давайте выясним, как это делается в данном приложении.
Видео:Табулирование функции и построение графика в ExcelСкачать

Использование табулирования
Табулирование применяется путем создания таблицы, в которой в одной колонке будет записано значение аргумента с выбранным шагом, а во второй — соответствующее ему значение функции. Затем на основе расчета можно построить график. Рассмотрим, как это делается на конкретном примере.
Создание таблицы
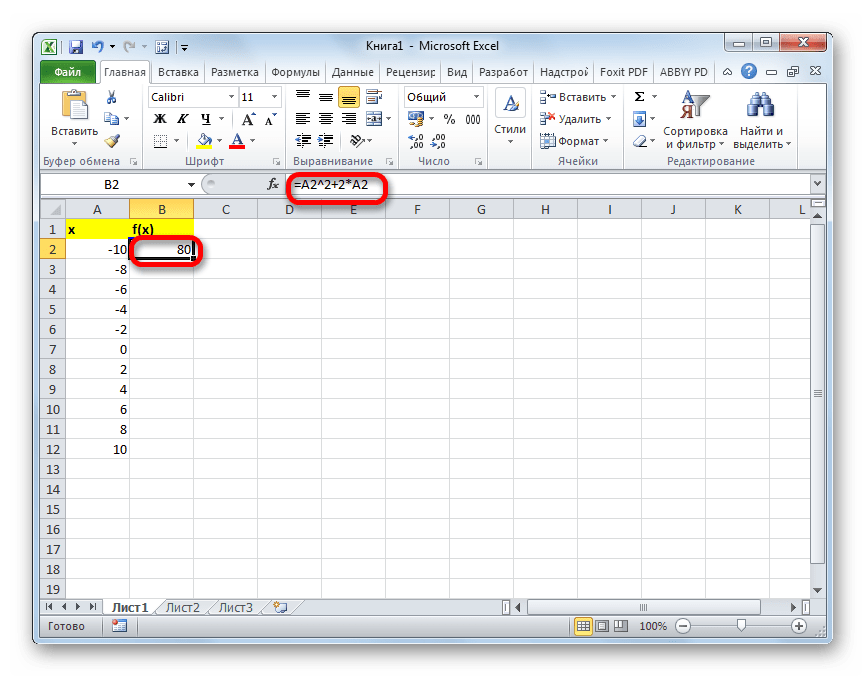
Создаем шапку таблицы с колонками x, в которой будет указано значение аргумента, и f(x), где отобразится соответствующее значение функции. Для примера возьмем функцию f(x)=x^2+2x, хотя для процедуры табулирования может использоваться функция любого вида. Устанавливаем шаг (h) в размере 2. Граница от -10 до 10. Теперь нам нужно заполнить столбец аргументов, придерживаясь шага 2 в заданных границах.
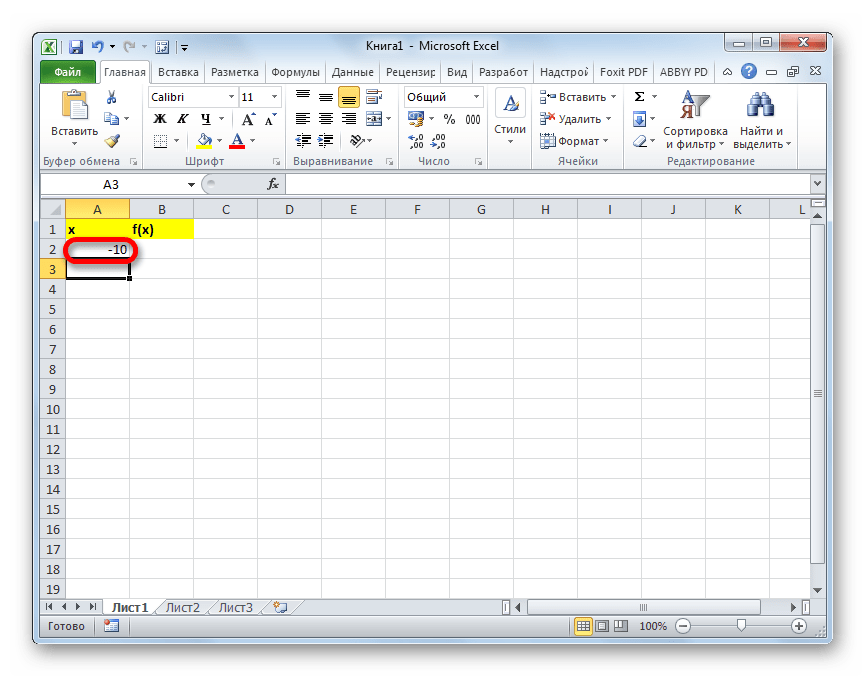
- В первую ячейку столбца «x» вписываем значение «-10». Сразу после этого жмем на кнопку Enter. Это очень важно, так как если вы попытаетесь произвести манипуляцию мышкой, то значение в ячейке превратится в формулу, а в данном случае это не нужно.
Все дальнейшие значения можно заполнить вручную, придерживаясь шага 2, но удобнее это сделать с помощью инструмента автозаполнения. Особенно этот вариант актуален, если диапазон аргументов большой, а шаг — относительно маленький.
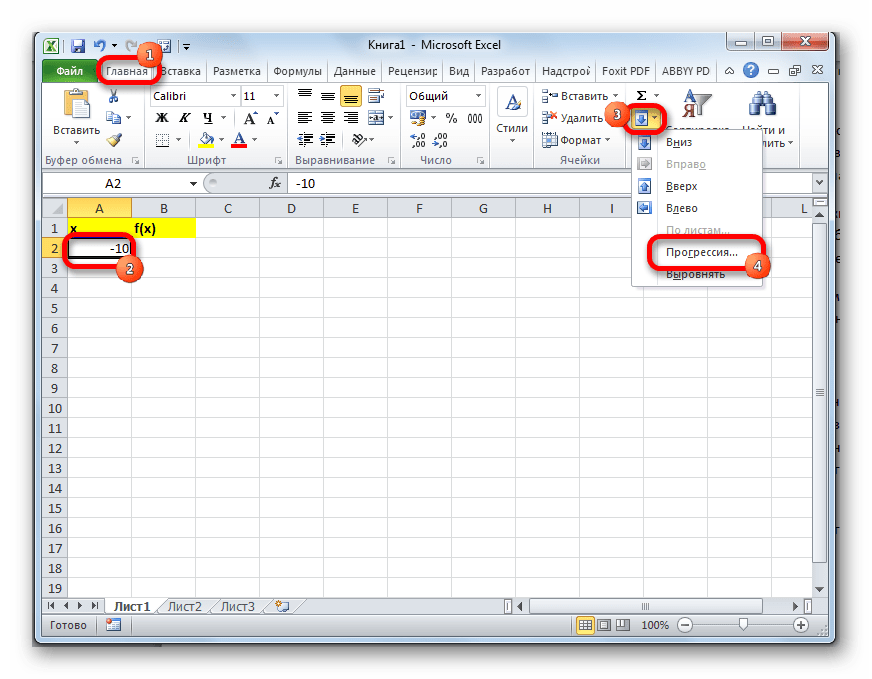
Выделяем ячейку, в которой содержится значение первого аргумента. Находясь во вкладке «Главная», кликаем по кнопке «Заполнить», которая размещена на ленте в блоке настроек «Редактирование». В появившемся списке действий выбираем пункт «Прогрессия…».
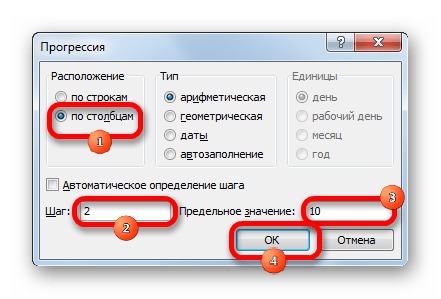
Открывается окошко настройки прогрессии. В параметре «Расположение» устанавливаем переключатель в позицию «По столбцам», так как в нашем случае значения аргумента будут размещаться именно в колонке, а не в строке. В поле «Шаг» устанавливаем значение 2. В поле «Предельное значение» вписываем число 10. Для того чтобы запустить прогрессию, жмем на кнопку «OK».
При этом, вместо значения x подставляем координаты первой ячейки из столбца с аргументами. Жмем на кнопку Enter, чтобы вывести результат вычислений на экран.
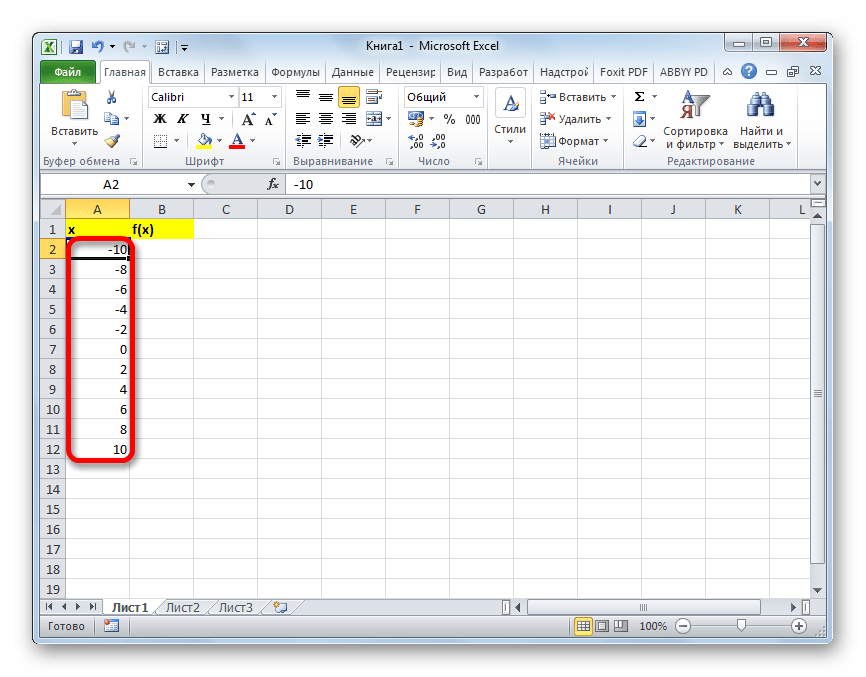
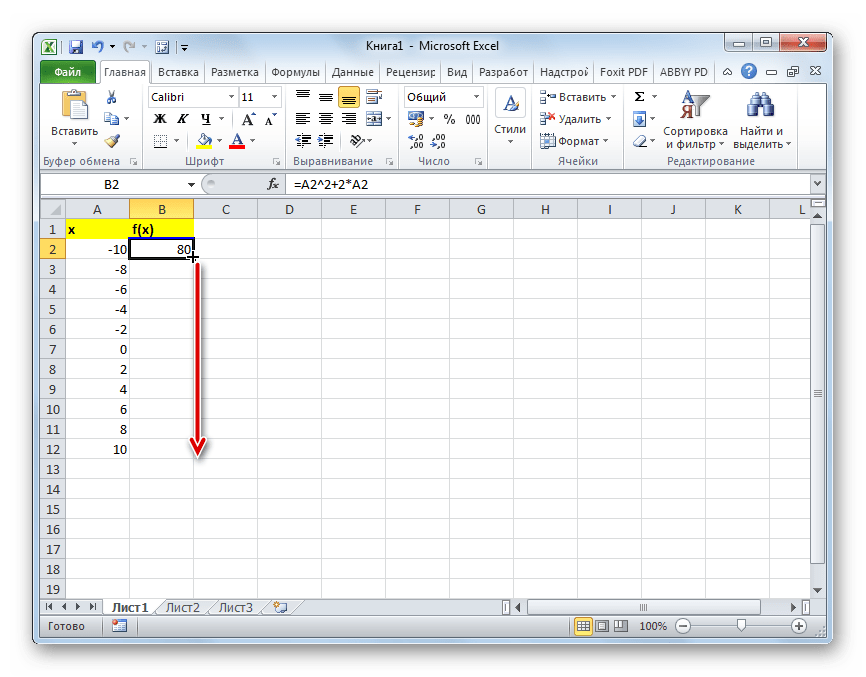
Для того, чтобы произвести вычисление функции и в других строках, снова воспользуемся технологией автозаполнения, но в данном случае применим маркер заполнения. Устанавливаем курсор в нижний правый угол ячейки, в которой уже содержится формула. Появляется маркер заполнения, представленный в виде небольшого по размеру крестика. Зажимаем левую кнопку мыши и протягиваем курсор вдоль всего заполняемого столбца.
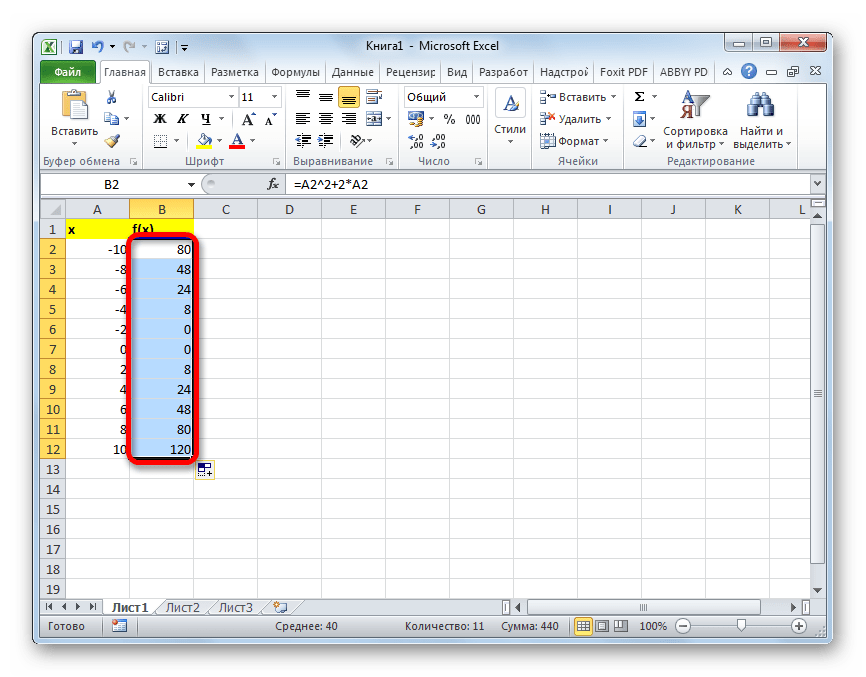
Таким образом, табуляция функции была проведена. На её основе мы можем выяснить, например, что минимум функции (0) достигается при значениях аргумента -2 и 0. Максимум функции в границах вариации аргумента от -10 до 10 достигается в точке, соответствующей аргументу 10, и составляет 120.
Построение графика
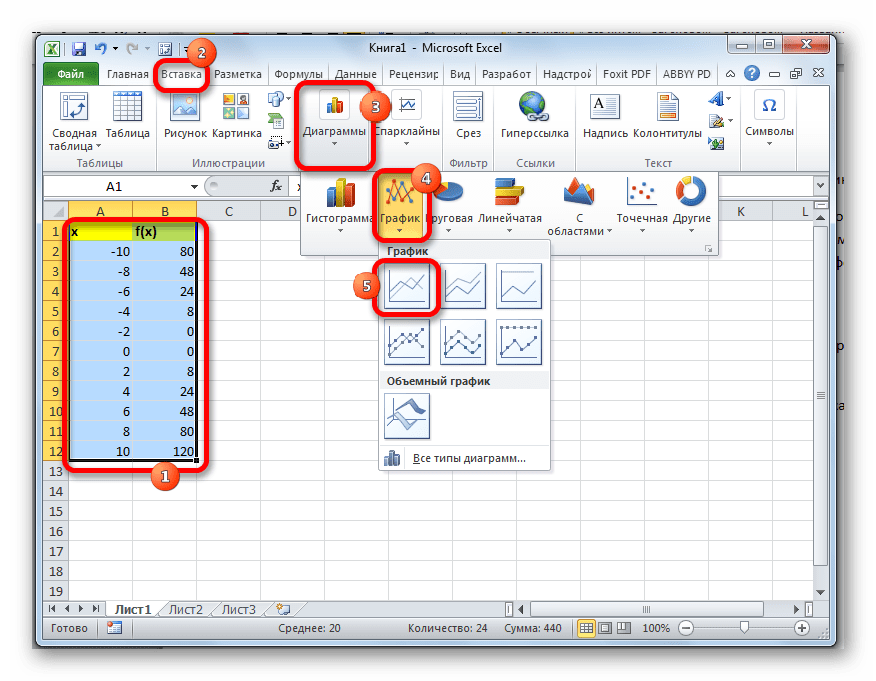
На основе произведенной табуляции в таблице можно построить график функции.
- Выделяем все значения в таблице курсором с зажатой левой кнопкой мыши. Перейдем во вкладку «Вставка», в блоке инструментов «Диаграммы» на ленте жмем на кнопку «Графики». Открывается список доступных вариантов оформления графика. Выбираем тот вид, который считаем наиболее подходящим. В нашем случае отлично подойдет, например, простой график.
Далее по желанию пользователь может отредактировать график так, как считает нужным, используя для этих целей инструменты Excel. Можно добавить названия осей координат и графика в целом, убрать или переименовать легенду, удалить линию аргументов, и т.д.
Как видим, табулирование функции, в общем, процесс несложный. Правда, вычисления могут занять довольно большое время. Особенно, если границы аргументов очень широкие, а шаг маленький. Значительно сэкономить время помогут инструменты автозаполнения Excel. Кроме того, в этой же программе на основе полученного результата можно построить график для наглядного представления.
Помимо этой статьи, на сайте еще 12708 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Видео:Табулирование функцииСкачать

Лабораторная работа №2 «Табулирование функции»
ЛАБОРАТОРНАЯ РАБОТА №2
Табулирование функции представляет собой достаточно простую по своей концепции математическую задачу, связанную с составлением некоторой таблицы, в которую заносят значения независимой переменной (аргумента) х и соответствующих им значения зависимой переменной (функции) у.
В качестве примера выполним табулирование функции следующего вида:
на множестве значений аргумента от 0 до 5 с шагом его изменения равным 0,5.
1. Выделите все ячейки ЭТ и установите ширину ее столбцов равной 9 единицам. Примените к ячейкам ЭТ шрифт «Times New Roman Cyr», начертание обычное, размер кегля 12 пунктов. Выберите масштаб отображения ЭТ равным 75%.
2. Введите в ячейку A1 строку «Лабораторная работа «Табулирование функции». В ячейки A3:A5 введите заголовки строк расчетной таблицы: «№ шага», «Аргумент» и «Функция» соответственно.
4. В ячейки B3:L3 введите методом автозаполнения номера шагов расчета от 1 до 11, а в ячейки B4:L4 – расчетные значения аргумента.
5. В ячейку B5 введите формулу расчета значения функции
=5*exp(-B4)*cos(5*B4) для значения аргумента, хранящегося в ячейке B4. Методом автозаполнения скопируйте эту расчетную формулу в правые соседние ячейки до L5 включительно.
6. Выполните форматирование заголовка таблицы, содержимого ячеек и их границ. Для этого:


6.3. Щелкните мышкой по стрелке расширения списка кнопки «Границы», расположенную на панели инструментов «Форматирование», и отбуксируйте панель «Границы» в поле ЭТ (для Вашего удобства работы с инструментами данной панели). Выделите блоки ячеек А3:L5 и примените к ним операции форматирования границ.
Правильный результат создания электронной таблицы, предназначенной для решения математической задачи, связанной с табуляцией средствами программы Excel функции указанного выше вида, представлен на рис.
Рис. Электронная таблица табулирования функции.
Выполните табулирование одного из вариантов функций на множестве значений аргумента от 0 до 5 с шагом его изменения равным 0,5.
Номер варианта должен совпадать с номером в списке вашей группы
📸 Видео
Решение ОДУ 1 го порядка в ExcelСкачать

Корни, экстремумы, исследование уравнений, функций в Excel. Часть 2Скачать

MS Excel - Ввод формулСкачать

Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать

Создание сложных функций в Microsoft ExcelСкачать

Excel график функцииСкачать

Решение уравнения практикаСкачать

Математический анализ, 15 урок, АссимптотыСкачать

Урок 4. Формулы Excel для начинающихСкачать
Математика без Ху!ни. Исследование функции, график. Первая, вторая производная, асимптоты.Скачать

Производная: секретные методы решения. Готовимся к ЕГЭ | Математика TutorOnlineСкачать

23 Функция ЕСЛИ в Excel (IF)Скачать

Математический анализ, 16 урок, Исследование функции и построение графикаСкачать

10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

10 класс, 10 урок, Обратная функцияСкачать

Математика Без Ху!ни. Производная сложной функции.Скачать