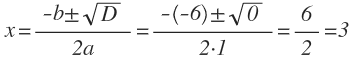Таблица дискриминантов в квадратном уравнении (5 видео)

Дискриминант квадратного уравнения

Дискриминант квадратного уравнения — это выражение, находящееся под корнем в формуле нахождения корней квадратного уравнения. Дискриминант обозначается латинской буквой D.

Вид уравнения	Формула корней	Формула дискриминанта
ax 2 + bx + c = 0		b 2 — 4ac
ax 2 + 2kx + c = 0		k 2 — ac
x 2 + px + q = 0
x 2 + px + q = 0		p 2 — 4q

Все формулы нахождения корней квадратных уравнений можно записать короче с помощью дискриминанта:

Вид уравнения	Формула
ax 2 + bx + c = 0	, где D = b 2 — 4ac
ax 2 + 2kx + c = 0	, где D = k 2 — ac
x 2 + px + q = 0	, где D =
x 2 + px + q = 0	, где D = p 2 — 4q

Дискриминант позволяет определить, имеет ли уравнение корни и сколько их, не решая само уравнение:

Если дискриминант больше нуля, то уравнение имеет два корня.
Если дискриминант равен нулю, то уравнение имеет один корень.
Если дискриминант меньше нуля, то уравнение не имеет корней.

Несмотря на то, что есть несколько формул дискриминанта, чаще всего используют первую:

так как она относится к формуле:

которая является универсальной формулой нахождения корней квадратного уравнения. Данная формула подходит даже для неполных квадратных уравнений.

Содержание

Решение квадратных уравнений через дискриминант
Как найти дискриминант квадратного уравнения
Понятие квадратного уравнения
Понятие дискриминанта
Как решать квадратные уравнения через дискриминант
Примеры решения квадратных уравнений с помощью дискриминанта
Квадратное уравнение
📺 Видео

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Решение квадратных уравнений через дискриминант

Для решения квадратного уравнения по формуле можно сначала вычислить дискриминант и сравнить его с нулём. В зависимости от результата, либо искать корни по формуле, либо сделать вывод, что корней нет.

Пример 1. Решить уравнение:

Определим, чему равны коэффициенты:

D = b 2 — 4ac = (-4) 2 — 4 · 3 · 2 = 16 — 24 = -8,

Определим, чему равны коэффициенты:

D = b 2 — 4ac = (-6) 2 — 4 · 1 · 9 = 36 — 36 = 0,

Уравнение имеет всего один корень:

Определим, чему равны коэффициенты:

D = b 2 — 4ac = (-4) 2 — 4 · 1 · (-5) = 16 + 20 = 36,

Видео:Как решить квадратное уравнение за 30 секунд#математика #алгебра #уравнение #дискриминант #репетиторСкачать

Как найти дискриминант квадратного уравнения

О чем эта статья:

Видео:Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Понятие квадратного уравнения

Уравнение — это равенство, содержащее переменную, значение которой нужно найти.

Например, х + 8 = 12 — это уравнение, содержащее переменную х.

Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.

Например, если х = 5, то при подстановке в уравнение мы получим:

13 = 12 — противоречие.

Значит, х = 5 не является корнем уравнения.

Если же х = 4, то при подстановке в уравнение мы получим:

12 = 12 — верное равенство.

Значит, х = 4 является корнем уравнения.

Решить уравнение — значит найти все его корни или доказать, что их не существует.

Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Если все коэффициенты в уравнении отличны от нуля, то уравнение называется полным.

Такое уравнение можно решить с помощью формулы дискриминанта.

Видео:ТЕОРЕМА ВИЕТА ЗА 2 МИНУТЫСкачать

Понятие дискриминанта

Дискриминант квадратного уравнения — это выражение, равное b 2 − 4ac. Дискриминант в переводе с латинского означает «отличающий» или «различающий» и обозначается буквой D.

Дискриминант — отличный помощник, чтобы понять, сколько в уравнении корней.

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Как решать квадратные уравнения через дискриминант

Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:

Определим, чему равны коэффициенты a, b, c.

Вычислим значение дискриминанта по формуле D = b2 − 4ac.

Если дискриминант D 0, то у уравнения две корня, равные

Чтобы запомнить алгоритм решения полных квадратных уравнений и с легкостью его использовать, сохраните себе шпаргалку:

Видео:Формула корней квадратного уравнения. Алгебра, 8 классСкачать

Примеры решения квадратных уравнений с помощью дискриминанта

Пример 1. Решить уравнение: 3x 2 — 4x + 2 = 0.

Определим коэффициенты: a = 3, b = -4, c = 2.
Найдем дискриминант: D = b 2 — 4ac = (-4) 2 — 4 * 3 * 2 = 16 — 24 = -8.

Ответ: D 2 — 6x + 9 = 0.

Определим коэффициенты: a = 1, b = -6, c = 9.
Найдем дискриминант: D = b 2 — 4ac = (-6) 2 — 4 * 1 * 9 = 36 — 36 = 0.

D = 0, значит уравнение имеет один корень:

Ответ: корень уравнения 3.

Пример 3. Решить уравнение: x 2 — 4x — 5 = 0.

Определим коэффициенты: a = 1, b = -4, c = -5.
Найдем дискриминант: D = b 2 — 4ac = (-4) 2 — 4 * 1 * (-5) = 16 + 20 = 36.

D > 0, значит уравнение имеет два корня:

Ответ: два корня x₁ = 5, x₂ = -1.

Разобраться в решении квадратных уравнений на практике с классным преподавателем можно на курсах по математике в Skysmart.

Видео:Как решать квадратные уравнения без дискриминантаСкачать

Квадратное уравнение

Загляни сюда, – вдруг узнаешь себя!

Надеюсь, вы внимательно изучили таблицу, приведенную выше. Если все еще есть вопросы, – давайте разбираться.

Во первых, почему рассматриваются только случаи при ? Просто потому, что при у нас уже будет не квадратное уравнение, а линейное.

Формулу дискриминанта знают практически все, но почему же тогда возникают все же сложности с решением уравнений?

Начнем с того, что иногда происходит путаница с коэффициентами , и . Ни в коем случае мы не считаем, что – это тот коэффициент, что стоит на первом месте! Но – тот, что при . Давайте договоримся, что будем приводить всякое квадратное уравнение к стандартному виду, ставя на первое место слагаемое, содержащее , на последнее – свободный от член (если таковой имеется). Например, уравнение будем переписывать так .

Далее, некоторых может сбить с толку минусовой коэффициент при старшем члене (то есть ). В этом случае советую домножать обе части уравнения на -1. Например, встречая уравнение , переписывать его в таком виде , и только потом высчитывать дискриминант, находить корни.

И, наконец, замечу, находятся и такие товарищи, которые, встречая, например, уравнение , спешат выносить за скобку, путая это уравнение с неполным. Нет, это обычное полное квадратное уравнение, которое после переноса влево примет вид , – решаем мы его через дискриминант.

Поэтому, давайте договоримся всякое уравнение приводить к такому виду, чтобы справа стоял только ноль и ничего больше.

Плавно перешли к неполным квадратным уравнениям. Если мы будем придерживаться последного совета, то мы не сможем спутать неполное уравнение с полным уж это точно. Справа будет два слагаемых (вырожденный случай – одно), а не три как у полного уравнения. Можно, конечно, и такие уравнения решать через дискриминант,но проще поступить иначе.

У нас в случае неполного уравнения будет всегда получаться либо уравнение с двумя , либо с одним . Что делать, в случае, если у нас оба слагаемых содержат (например, )? Ну, конечно, выносить его за скобку (), в этом случае будем всегда получать, что произведение двух множителей равно . Когда такое возможно? Конечно, когда один из множителей равен нулю (либо , либо ). В этом случае у нас всегда один из корней будет нулевым.

Во втором же случае, неполное уравнение будет содержать лишь одно слагаемое с (например, или ). Если свободный член отрицательный (как в первом случае, ), то мы всегда сможем разложить левую часть на множители по формуле разность квадратов ( для уравнения имеем , далее ). Если же свободный член положителен, то уравнение не имеет корней (действительно, в уравнении первое слагаемое должно бы быть равным -3, чтобы в сумме с 3 дать 0, но такое невозможно).

В общем, каждое отдельно взятое квадратное уравнение мы решам одним из трех способов, – выбор не велик.

Заметим, также, что в случае полного квадратного уравнения в зависимости от того, какой дискриминант мы получаем, – на выходе разное количество корней. Если 0″ title=»Rendered by QuickLaTeX.com» height=»14″ width=»54″ style=»vertical-align: 0px;»/>, то будем иметь два корня, если , то имеем один корень (или два совпавших), наконец, если , то корней нет.