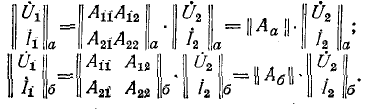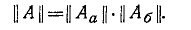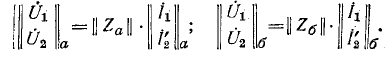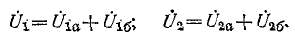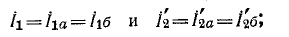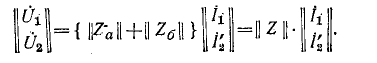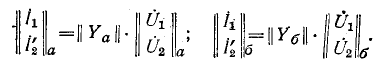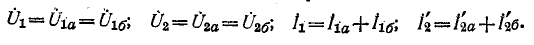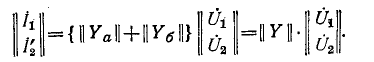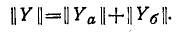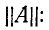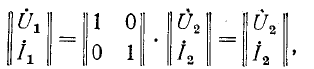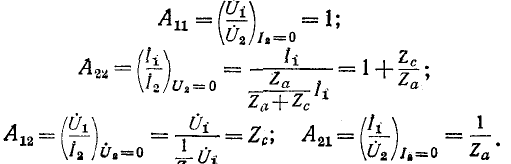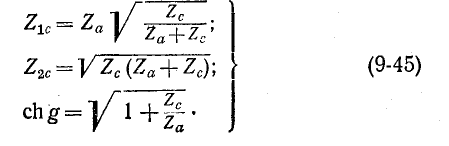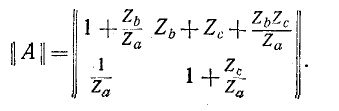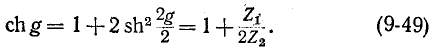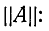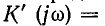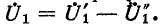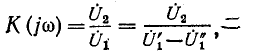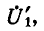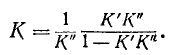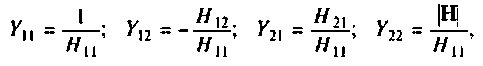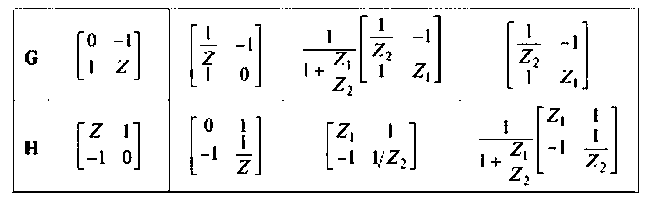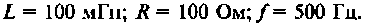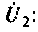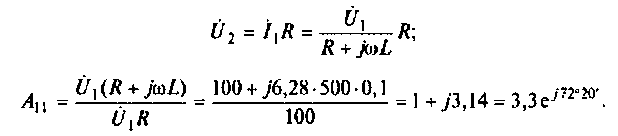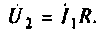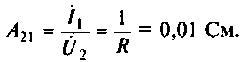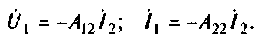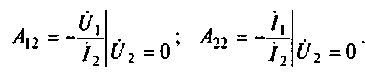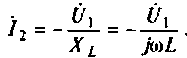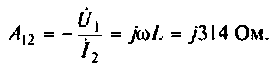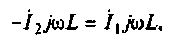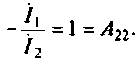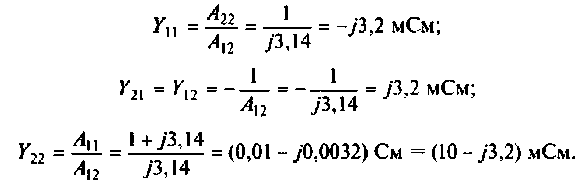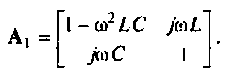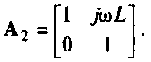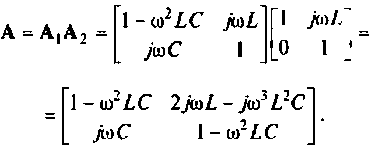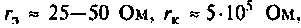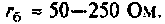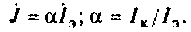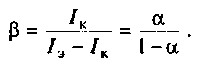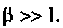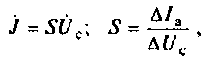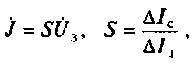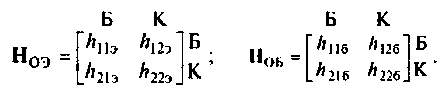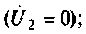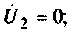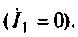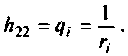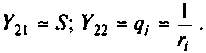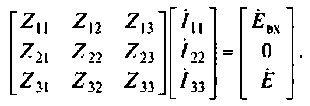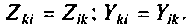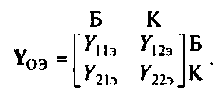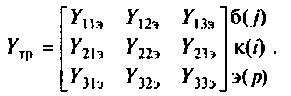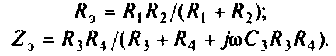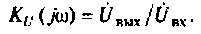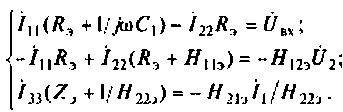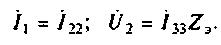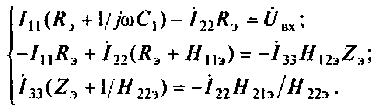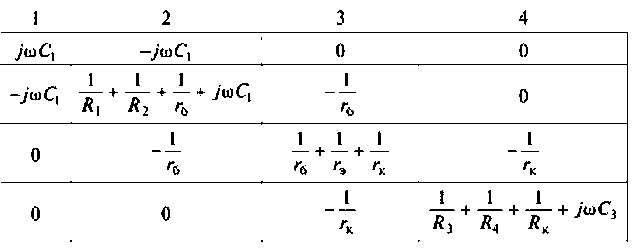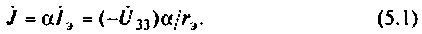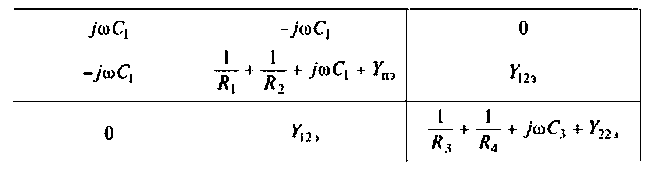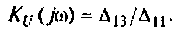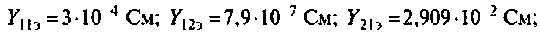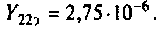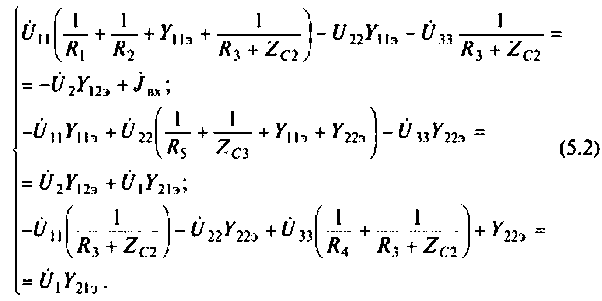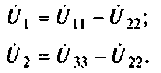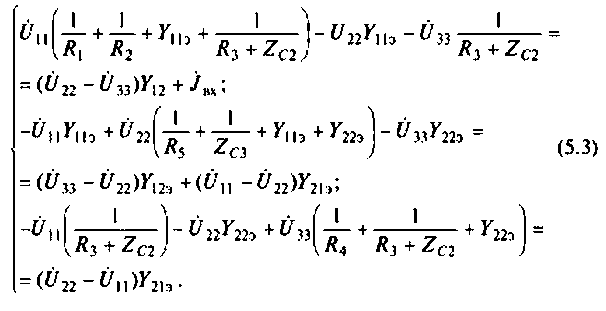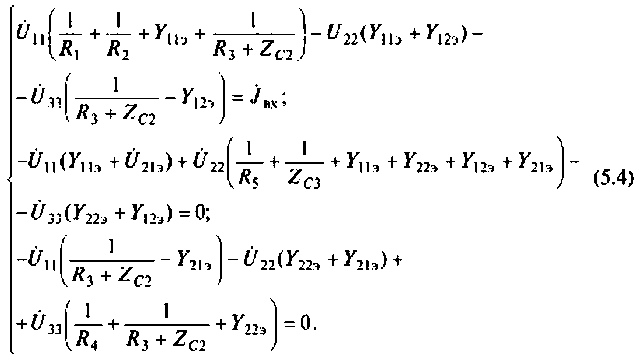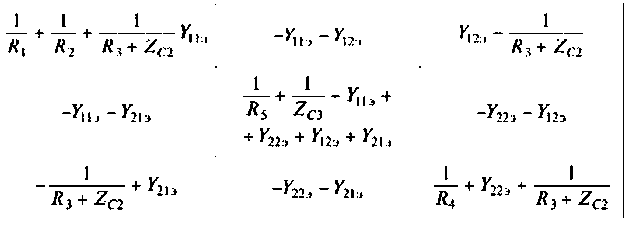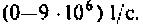Трехфазные асинхронные электродвигатели, или как их еще называют индукционные электродвигатели, являются наиболее распространенными в промышленности. Данный тип электродвигателя, аналогично машинам постоянного тока тоже обладают свойствами обратимости, и может работать как в двигательном, генераторном, так и в тормозных режимах – противовключение, динамическое торможение. Режим работы асинхронного электродвигателя характеризуют знаком и величиной скольжения.
Пожалуй, основным методом анализа установившихся режимов индукционного электродвигателя является использование эквивалентных схем замещения. В таком случае обычно рассматривают явление, которое относится к одной фазе многофазного двигателя при соединении его обмоток звездой.
Упрощенная картина магнитных потоков работающего асинхронного электродвигателя позволяет представить его в виде эквивалентной схемы:
Электромагнитная связь первичной и вторичной цепи осуществляется потоком взаимоиндукции Ф, индуктирующим в роторной обмотке ЭДС Е2S. Сопротивление индуктивное первичной цепи Х1 обусловлено наличием потока рассеивания, связанного только с этой цепью. Аналогично сопротивления Х2 обусловлено потоком рассеивания Ф25.
Частота тока ротора будет определяться скоростью его вращения относительно скорости вращения магнитного поля статора, то есть зависеть от скольжения и будет равна f2 = f1S.
Ток вторичной цепи при вращающемся роторе:
Также выражения для I2 может иметь:
Выше показанные выражения имеют не только различную форму записи, но и имеют совершенно разный физический смысл. А смысл его в том, что вместо вращающегося ротора можно рассматривать неподвижный, в котором будет индуцироваться ЭДС Е2. При этом индуктивное сопротивление будет равно Х2, а активное возрастет на величину 


- Т – образная схема замещения
- Г – образная схема замещения
- Режимы работы и схема замещения трансформатора
- Режим холостого хода трансформатора (ХХ)
- Режим короткого замыкания (КЗ)
- Четырехполюсники
- Холостой ход и короткое замыкание четырехполюсника
- Определение параметров четырехполюсника
- Повторное сопротивление и коэффициент распространения симметричного четырехполюсника
- Передаточные функции и обратные связи четырехполюсников
- Цепные схемы и электрические фильтры
- Параметры холостого хода и короткого замыкания
- Схемы замещения четырехполюсника
- Входное сопротивление четырехполюсника при произвольной нагрузке
- Характеристические параметры четырехполюсника
- Вносимое затухание четырехполюсника
- Передаточная функция
- Каскадное соединение четырехполюсников, основанное на согласовании характеристических сопротивлений
- Уравнения сложных четырехполюсников в матричной форме
- Одноэлементные четырехполюсники
- Г-образный четырехполюсник
- Т-образный и П-образный четырехполюсники
- Симметричный мостовой четырехполюсник
- Обратная связь
- Методы расчета электрических цепей с использованием теории четырехполюсников
- Краткая характеристика четырехполюсников
- Методы расчета линейных активных цепей с использованием теории четырехполюсников
- 📹 Видео
Видео:Лекция 183. Т - образная схема замещения 4-х полюсникаСкачать

Т – образная схема замещения
После приведения первичной и вторичной ЭДС они будут равны Е1 = Е2 / и это дает возможность соединить эквивалентные точки и получить такую схему:
Недостатком Т – образной схемы замещения помимо сложностей расчета, является зависимость всех токов I1, I2 / , Iμ от скольжения s.
Из Т – образной схемы замещения видно, что в режиме холостого хода, при I2 / = 0 и s = 0, ток в контуре будет обуславливаться сопротивлениями намагничивающего контура и первичной цепи и совсем не будет зависеть от скольжения. Данное обстоятельство позволит вынести на зажимы электродвигателя намагничивающий контур и перейти к Г – образной схеме замещения.
Видео:Схемы замещения четырехполюсниковСкачать

Г – образная схема замещения
Данная схема замещения позволяет изучать процессы в асинхронном электродвигателе, которые имеют место при изменении скольжения электрической машины.
Учет контура намагничивания необходим при определении I1, который потребляется из сети. Но Г — образная схема замещения будет справедлива лишь при наличии определенных допущений:
- Все цепи имеют неизменные (постоянные) параметры. Это значит, что приведенное вторичное сопротивление r2 / не будет зависеть от частоты цепи вторичной (ротора), а насыщение не будет влиять на реактивное сопротивление статорных и роторных обмоток Х1 и Х2 / ;
- Полная проводимость намагничивающего контура принимается неизменной, а ток намагничивания, независимо от нагрузки, будет всегда пропорционален напряжению, приложенному к обмоткам;
- Потери добавочные не учитываются;
- Паразитные моменты, создаваемые высшими гармониками МДС, также не учитывают.
Следует также помнить и то, что в Г – образной схеме замещения в величины сопротивлений необходимо внести соответствующие поправки:
В выше перечисленных уравнениях величины имеющие индекс «дейст» соответствуют реальным значениям параметров асинхронной машины, а без индексов – те, которые используют в эквивалентной схеме.
Поскольку отношение r1/xμ довольно таки мало, то практически довольно часто принимают:
Обычно δ лежит в пределах 1,05 – 1,1.
Первичный ток I1 будет равен при любом скольжении:
Приведенный роторный ток:
Показанное выше выражение показывает, что ток ротора является функцией скольжения. При s = 0 I2 / = 0. При увеличении скольжения I2 / также будет расти, а при s = 1 достигнет своего максимума, или тока короткого замыкания, или пускового:
Если в роторной цепи отсутствует добавочное сопротивление (АД с КЗ ротором), пусковой ток может достигнуть довольно приличных значений, а именно 5 – 8 раз больше чем его номинальное значение.
Данная зависимость показана ниже:
Отношения пускового значения к номинальному является очень важным параметром для асинхронных машин с короткозамкнутым ротором, так как наличие пусковых токов приводит к просадкам напряжения, что особо ощутимо при использовании электродвигателей средней и большой мощности. Поэтому данная характеристика приводится в каталогах по выбору электрических машин.
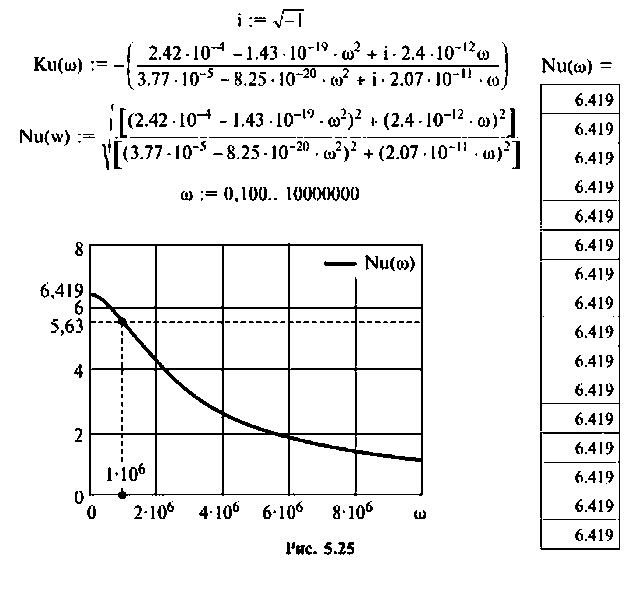
Видео:Задачи по четырехполюсникам. Т-образная схемаСкачать
Режимы работы и схема замещения трансформатора
Схема замещения трансформатора позволяет отдельно расчитывать цепи первичной и вторичных обмоток. В схему замещения трансформатора входят поля рассеивания магнитного потока, а вторичные цепи пересчитываются в первичную через коэффициенты трансформации.
Для составления схемы замещения возьмём трансформатор с двумя обмотками: первичной с количеством витков W1 для подключения к сети питания и вторичной с количеством витков W2 для подключения нагрузки. Его упрощенное устройство показано на рисунке 1.
Рисунок 1 Упрощенное устройство трансформатора
Принципиальная схема подключения нагрузки к источнику питания через трансформатор приведена на рисунке 2.
Рисунок 2 Принципиальная схема подключения нагрузки через трансформатор
Для создания схемы замещения трансформатора нам потребуются три режима его работы: режим холостого хода (ХХ), рабочий режим (номинальный режим) и режим короткого замыкания (КЗ). Режимы холостого хода и короткого замыкания трансформатора позволяют определить значения элементов схемы замещения трасформатора. Рассмотрим работу трансформатора в этих режимах.
Видео:Лекция 184. П - образная схема замещения 4-х полюсникаСкачать

Режим холостого хода трансформатора (ХХ)
В этом режиме сопротивление нагрузки равно бесконечности, в результате чего можно не учитывать вторичную обмотку и трансформатор работает как обычная катушка индуктивности с ферромагнитным сердечником. Кроме того, в режиме холостого хода трансформатора определяют его коэффициент трансформации. Схема замещения трасформатора в режиме холостого хода приведена на рисунке 3.
Рисунок 3 Схемы замещения трансформатора для режима холостого хода:
а — последовательная схема замещения,
б — параллельная схема замещения
На эквивалентных схемах трансформатора, приведенных на рисунке 2, показаны:
Индуктивность первичной обмотки, которая вместе с потерями в сердечнике влияет на к.п.д. трансформатора, можно рассчитать по следующей формуле:

Параллельная эквивалентная схема трансформатора более удобна по сравнению с последовательной для построения векторной диаграммы напряжений и токов для реальной катушки индуктивности. Эта диаграмма приведена на рисунке 3.
Рисунок 3 Векторная диаграмма напряжений и токов трансформатора в режиме холостого хода
Здесь δ — угол потерь в магнитопроводе
X1 — сопротивление индуктивности рассеяния LS1.
Обратите внимание, что в этом режиме работы трансформатора вектор ЭДС индуцированный в обмотке W2 (напряжение во вторичной обмотке) совпадает по фазе с eL, а напряжение U1, подаваемое на первичную обмотку трансформатора, является суммой э.д.с. на индуктивности первичной обмотки и падения напряжения на сопротивлениях индуктивности рассеивания и активного сопротивления первичной обмотки:

Это выражение можно записать немного иначе:
При правильном проектировании трансформатора потери на омическом сопротивлении первичной обмотки малы, поскольку ток холостого хода много меньше номинального. Тогда угол сдвига фаз между током и напряжением (I10 и U1) определяется потерями в магнитопроводе. Это позволяет из опыта холостого хода и найти угол потерь δ и рассчитать потери в сердечнике.
Трансформатор является обращаемым устройством (первичную и вторичную обмотки можно поменять местами!), поэтому для каждой из обмоток записываем основную формулу трансформаторной ЭДС.


Разделив уравнение (3) на (4), получим выражение для коэффициента трансформации:

Подведем итоги Режим работы трансформатора на холостом ходе позволяет определить:
Коэффициент трансформации
Ток холостого хода I10 (для определения к.п.д.)
Видео:Лекция по электротехнике 4.4 - Схема замещения и уравнения Кирхгофа для неразветвленной цепиСкачать

Режим короткого замыкания (КЗ)
Этот режим в условиях эксплуатации является аварийным. Он применяется только для экспериментального определения индуктивности рассеивания трансформатора. Измерения проводят в следующей последовательности. Входное напряжение устанавливают равным нулю. Замыкают выходные клеммы (). Плавно поднимают входное напряжение (U1) до тех пор, пока в обмотках не установятся номинальные токи. Величина называется напряжением короткого замыкания, является паспортной величиной трансформатора и обычно составляет 5. 10% от номинального напряжения U1ном. При этом, ток холостого хода I10 весьма мал по сравнению с номинальным и им можно пренебречь (считать равным нулю). Тогда эквивалентная схема трансформатора в режиме КЗ принимает вид, показанный на рисунке 5.
Рисунок 5 Эквивалентная схема трансформатора в режиме короткого замыкания
Ток холостого хода мы приняли равным нулю , поэтому в эквивалентной схеме трансформатора параллельная цепь L0r0 отсутствует. Входное сопротивление трансформатора полностью определяются индуктивностью рассеивания первичной и вторичной обмоток, а также их омическим сопротивлением:

Результирующее сопротивление — это сопротивление короткого замыкания трансформатора. Зная полное сопротивление короткого замыкания:
можно найти коэффициент передачи трансформатора, а в случае малой индуктивности рассеивания потери мощности в обмотках трансформатора.
Намагничивающая сила, создающая магнитный поток в сердечнике в режиме короткого замыкания (измерительный режим) практически равна нулю:

и если I10 = 0, то откуда находим отношение токов, а значит и коэффициент трансформации по току:

Знак минус в формуле (15) говорит о том, что магнитные потоки Ф1 и Ф2 направлены навстречу друг другу и взаимно компенсируются.
Рабочий режим (нагруженный или номинальный). Если к вторичной обмотке W2 подключить нагрузку Rн, то ее напряжение U2 вызовет ток нагрузки I2, как это показано на рисунке 1б. Токи I1 и I2 ориентированы различно относительно магнитного потока Ф0. Ток I1 создает поток Ф1, а ток I2 создаёт поток Ф2 и стремится уменьшить поток Ф1. Иначе говоря, в магнитопроводе появляются магнитные потоки Ф1 и Ф2, которые на основании закона Ленца направлены встречно и их алгебраическая сумма даёт: — магнитный поток холостого хода трансформатора.
Отсюда можно записать уравнение намагничивающих сил (закон полного тока):

Видно, что изменение тока I2 обязательно приведёт к изменению тока I1. Нагрузка образует второй контур, в котором ЭДС вторичной обмотки е2 является источником энергии. При этом, справедливы уравнения:


где r2 — омическое сопротивление вторичной обмотки
х2 — сопротивление индуктивности рассеяния вторичной обмотки.
По закону Киргофа сумма токов (6) может быть обеспечена параллельным соединением электрических цепей, поэтому в рабочем режиме трансформатор можно представить эквивалентной схемой, приведенной на рисунке 4.
Рисунок 4 Схема замещения трансформатора в рабочем режиме
Эквивалентная схема трансформатора в рабочем режиме, приведенная на рисунке 4 называется Т-образной схемой замещения или приведённым трансформатором. Приведение вторичной обмотки к первичной выполняется при условии равенства полных мощностей вторичных обмоток 






Токи и напряжения приводятся через коэффициент трансформации, а сопротивления — через квадрат коэффициента трансформации. Можно пересчитать вторичную цепь в первичную или наоборот.
Представление трансформатора в виде эквивалентной схемы позволяет методами теории цепей рассчитать любую, сколь угодно сложную схему с трансформаторами.
Если у трансформатора есть несколько вторичных обмоток, как показано на условно-графическом изображении трансформатора, приведенном на рисунке 6а, то пересчитанные сопротивления нагрузки на эквивалентной схеме соединяются параллельно и его эквивалентная схема принимает вид, показанный на рисунке 6б.
Рисунок 6 Схема замещения трансформатора с двумя вторичными обмотками
При этом значение импеданса (полного сопротивления) вторичных обмоток Z2 находится как сумма сопротивлений вторичных обмоток и сопротивления их индуктивностей рассеивания:
Понравился материал? Поделись с друзьями!
- Алиев И.И. Электротехнический справочник. – 4-е изд. испр. – М.: ИП Радио Софт, 2006. – 384с.
- Схема замещения трансформатора
- Режимы работы трансформатора
- Параметры схемы замещения трансформатора
Вместе со статьей «Режимы работы и схема замещения трансформатора» читают:
Видео:Лекция 080-4. Теория четырехполюсников. Схемы замещения четырехполюсниковСкачать

Четырехполюсники
Содержание:
Основы теории четырехполюсников и фильтров:
Электрическая цепь, имеющая два входных и два выходных зажима, называется четырехполюсником. Теория четырехполюсников в общем виде рассматривает основную проблему электротехники: передачу энергии от источника к приемнику через промежуточное звено — четырехполюсник.
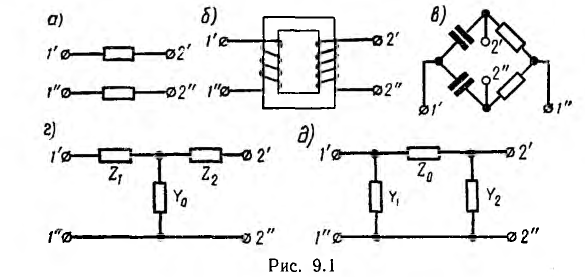
Активные четырехполюсники содержат внутри себя также источники электрической энергии. Далее сначала рассматриваются пассивные четырехполюсники, не содержащие внутри себя источников энергии. Примером их могут служить линия передачи (рис. 9.1, а), трансформатор (рис. 9.1, б), мостовая схема (рис. 9.1, в), а также Т-образная (рис. 9.1, г) и П-образная (рис. 9.1, д) схемы, к зажимам I’, I» которых подключается источник, а к зажимам 2′, 2″ — приемник электрической энергии.
На рис. 9.2, а изображена в общем виде схема четырехполюсника. Здесь
Для вывода уравнений, связывающих входные и выходные напряжения и токи, удобно заменить приемник Z2 с напряжением 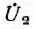
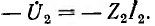
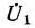
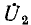
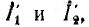
Аналогично, при наличии источника 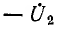
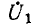
Здесь 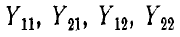
Действительные токи на входе и выходе четырехполюсника
Совместное решение этих уравнений дает
После введения обозначений
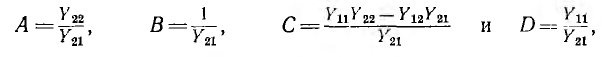
получаются уравнения четырехполюсника:
где комплексы А, В, С, D называются параметрами четырехполюсника. Между ними существует следующая связь:
Следовательно, из четырех параметров независимыми являются три.
Если входные и выходные зажимы поменять местами (рис. 9.2, д), т. е. осуществить обратное питание (индекс «о»), уравнения, очевидно, получатся аналогичными:
а параметры А’, В’, С’, D’ определятся из выражений (9.1), если индекс I заменить индексом 2 и наоборот:
Следовательно, уравнения четырехполюсника, питаемого со стороны выхода, получают вид:
Отсюда следует, что в симметричном четырехполюснике, который со стороны выходных зажимов представляет ту же цепь, что и со стороны входных, А = D и А 2 — ВС = 1.
С помощью уравнений четырехполюсника можно определить нагрузочный режим, т. е. найти 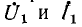
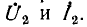
Видео:Решение биквадратных уравнений. 8 класс.Скачать

Холостой ход и короткое замыкание четырехполюсника
При холостом ходе ток на выходе 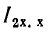
При коротком замыкании напряжение на выходе 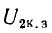
Отсюда видно, что параметр А представляет собой отношение входного и выходного комплексных напряжений при холостом ходе четырехполюсника, a D — отношение входного и выходного комплексных токов при коротком замыкании.
Если при холостом ходе напряжение на выходе будет равно напряжению 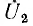
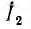
Следовательно, напряжение 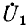
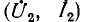
Чтобы осуществить это наложение, надо знать, как расположить друг относительно друга векторные диаграммы холостого хода 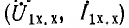
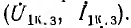
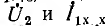
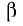
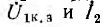
После этого построение ведется в следующем порядке (рис. 9.3): строится заданная диаграмма 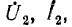
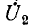
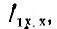
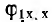
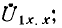
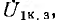
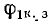
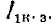
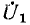
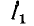
Так как в симметричном четырехполюснике А = D, то
т. е. угол сдвига фаз между векторами 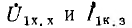
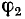
Указанное применение принципа наложения имеет большое значение при испытании мощных электротехнических устройств, описываемых линейными уравнениями, так как позволяет заменить опыт нагрузки, требующий источников большой мощности, опытами холостого хода и короткого замыкания при значительно меньшей мощности.
Видео:10-2 Составление схем замещения и расчет несимметричного ТКЗСкачать

Определение параметров четырехполюсника
Если известны конкретная схема и сопротивления (проводимости) ветвей четырехполюсника, то его параметры могут быть определены расчетным путем по входным и взаимным проводимостям. Можно также исходить непосредственно из зависимостей, устанавливаемых законами Кирхгофа.
Далее в качестве примера рассмотрены простейшие схемы четырехполюсников. Так как из четырех параметров четырехполюсника независимыми являются три, простейшие схемы должны содержать три ветви, т. е. представлять собой соединение звездой (Т-образная схема, рис. 9.1, г) или треугольником (П-образная схема, рис. 9.1, д).
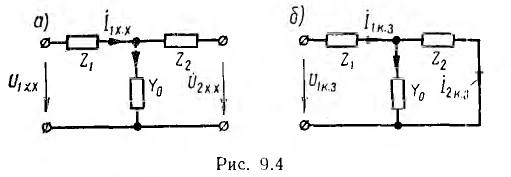
Для Т-образной схемы при режиме холостого хода (рис. 9.4, а) очевидны следующие соотношения:
при коротком замыкании (рис. 9.4, б)
Отсюда параметры этого четырехполюсника
Параметры П-образной схемы могут быть определены аналогичным расчетом (рис. 9.1, д). При холостом ходе
при коротком замыкании
Отсюда параметры П-схемы
Подобно тому, как при расчете цепей любой двухполюсник удобно заменить простейшим эквивалентным двухполюсником — последовательной или параллельной схемой, можно любой сложный четырехполюсник заменить простейшим эквивалентным ему, т. е. Т- или П-схемой. Решая уравнения (9.2) и (9.3), можно найти параметры этих эквивалентных схем, выразив их через параметры четырехполюсника.
Из этих выражений видно, что схемы, эквивалентные симметричным четырехполюсникам, сами тоже симметричны, так как, если А = D, то
Если конкретная схема и параметры ветвей четырехполюсника неизвестны, его параметры могут быть определены из опытов холостого хода и короткого замыкания при питании и измерениях со стороны входа и со стороны выхода. Эти измерения позволяют определить комплексы сопротивлений короткого замыкания 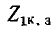
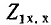
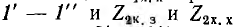
Как видно из этих выражений, полные сопротивления при коротком замыкании и холостом ходе связаны между собой соотношением:
поэтому из четырех вышеупомянутых опытов необходимы лишь три, а четвертый может служить для контроля.
Параметры четырехполюсника находят по формулам, вытекающим из (9.4):
Видео:2. Моделирование асинхронного двигателя на основе Г-образной схемы замещенияСкачать

Повторное сопротивление и коэффициент распространения симметричного четырехполюсника
В технике электросвязи часто применяются симметричные четырехполюсники и такое согласование их с сопротивлением нагрузки Z, при котором сопротивление между входными зажимами также равно Z, т. е.
Сопротивление Z получило название повторного. Уравнения симметричного четырехполюсника после подстановки 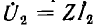
Деление первого уравнения на второе дает:
откуда
и уравнения четырехполюсника, нагруженного повторным сопротивлением, будут иметь вид:
Как видно из этих уравнений, равные между собой отношения напряжений 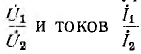
Следовательно, у симметричного четырехполюсника, нагруженного повторным сопротивлением, выходные напряжение и ток меньше входных в 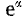
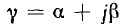
уравнения симметричного четырехполюсника при произвольной нагрузке могут быть переписаны в другой форме:
Видео:Уроки-2 и 3.Схемы замещения и параметры двухобмоточного и трехобмоточного трансформатораСкачать

Передаточные функции и обратные связи четырехполюсников
Как видно из предыдущего, четырехполюсник можно рассматривать как преобразователь входных величин 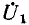
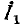
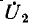
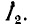
Очевидно, что первая передаточная функция безразмерна, вторая имеет размерность сопротивления, третья — проводимости.
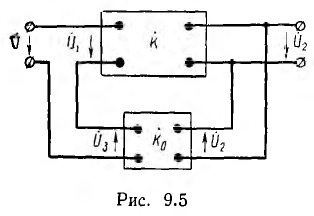
В ряде электротехнических и автоматических устройств необходимо, чтобы передаточная функция зависела от режима цепи на выходе. Для этого схема усложняется обратной связью — дополнительным четырехполюсником, питаемым выходной величиной основного четырехполюсника, например напряжением 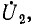
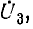
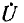
Пусть передаточная функция четырехполюсника обратной связи равна 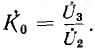
окуда передаточная функция всей системы
Из этого выражения видно, что передаточную функцию К’ системы можно изменять, регулируя передаточную функцию Ко устройства обратной связи.
Цепные схемы и электрические фильтры
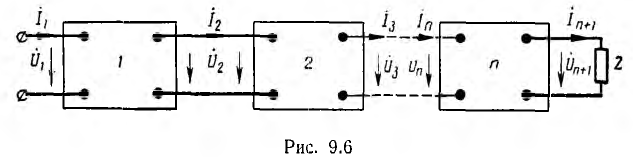
Цепные схемы состоят из каскадно включенных четырехполюсников, называемых звеньями (рис. 9.6).
При этом выходные зажимы каждого предыдущего звена соединяются с входными последующего. Если все n четырехполюсника одинаковы и симметричны, а последний нагружен своим повторным сопротивлением Z, то оно будет также входным сопротивлением последнего звена, нагрузкой предпоследнего звена, его входным сопротивлением и т. д. Величина 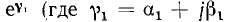
Тогда уравнения n-звенной цепной схемы будут:
В различных электротехнических устройствах между источником энергии и приемником включают электрические фильтры в виде четырехполюсников или цепных схем, чтобы пропустить к приемнику только токи заданного диапазона частоты.
Фильтры различаются по диапазону пропускаемых частот: низкочастотные — от 0 до заданного значения ω, высокочастотные — от ω до 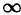
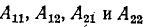
В случае перемены направления передачи электрической энергии, а именно при передаче энергии от выводов 2 к выводам 1, в уравнениях четырехполюсника связывают напряжения и токи 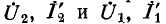
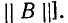
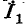
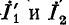
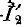
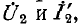
Сопоставляя уравнение (9-18) с уравнениями (9-3), соответствующими направлению передачи энергии от выводов 1 к выводам 2, заключаем, что с переменой направления передачи энергии коэффициенты 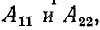
Параметры холостого хода и короткого замыкания
Было показано, что коэффициенты 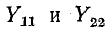
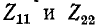
Введя индексы «к» и «х» для обозначения режимов короткого замыкания (выводы замкнуты) и холостого хода (выводы разомкнуты), получим параметры холостого хода и короткого замыкания:
Этих параметров достаточно для составления уравнений обратимого четырехполюсника. Для записи уравнений необратимого четырехполюсника недостаточно параметров холостого хода и короткого замыкания, так как из них только три являются независимыми.
Действительно, на основании (9-19) и таблицы приложения II
и
откуда
Таким образом, параметры холостого хода и короткого замыкания, выражаемые формулами (9-19), принудительно связаны уравнением (9-20).
В случае симметричного четырехполюсника
т. е. симметричный четырехполюсник характеризуется только двумя параметрами.
Параметры холостого хода и короткого замыкания могут быть выражены через любую систему коэффициентов, например через коэффициенты А: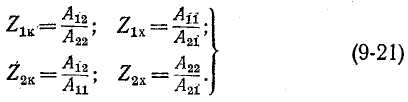
В свою очередь любая система коэффициентов обратимого четырехполюсника может быть выражена через параметры холостого хода и короткого замыкания. Например, для коэффициентов А получаем 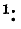
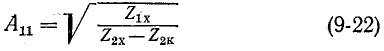
и, используя (9-21), выражаем все остальные коэффициенты через
Схемы замещения четырехполюсника
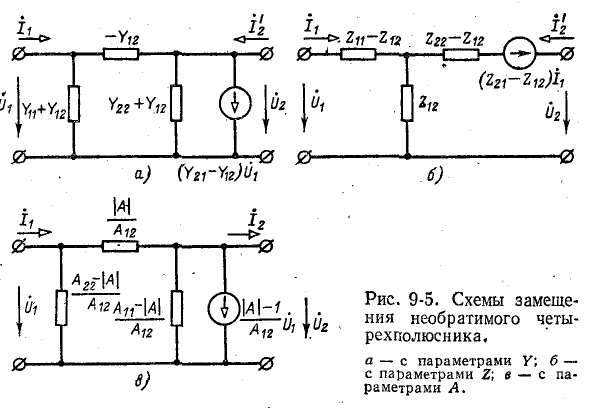
На основании уравнений четырехполюсника могут быть построены различные схемы замещения, которые облегчают исследование общих свойств рассматриваемой цепи. Ниже показаны некоторые схемы замещения четырехполюсника, параметры которых выражаются через коэффициенты У, Z и А.
1 Эта формула дает двузначное решение, так как входящие в нее параметры не меняются от перекрещивания любой пары выводов.
На практике чаще всего пользуются П-образной и Т-образной схемами замещения четырехполюсника.
На рис. 9-5, а показана П-образная схема замещения четырехполюсника, в которой проводимости ветвей выражены через коэффициенты Y. При этом зависимый источник тока 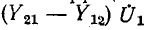
только в случае необратимого четырехполюсника; в схеме обратимого четырехполюсника 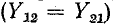
Схема рис. 9-5, о соответствует системе уравнений (9-1). Действительно, по первому закону Кирхгофа ток 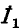
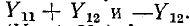
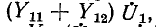
В свою очередь ток 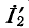
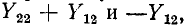
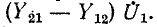
На рис. 9-5, б показана Т-образная схема замещения, в которой сопротивления ветвей выражены через коэффициенты Z четырехполюсника. Применив второй закон Кирхгофа, легко убедиться в тем, что данная схема соответствует уравнениям (9-2).
Схема замещения четырехполюсника содержит зависимый источник э. д. с. или тока в случае, когда четырехполюсник необратим. В схеме обратимого четырехполюсника 
Параметры схемы замещения четырехполюсника могут быть выражены также через коэффициенты А. Так, например, пользуясь таблицей приложения II, можно в П-об-разной схеме (см. рис. 9-5, а) проводимости ветвей выразить через коэффициенты А. при этом получится схема рис. 9-5, в в случае обратимого четырехполюсника будем иметь схему рис. 9-6, а, которая часто применяется для расчета энергетических систем.
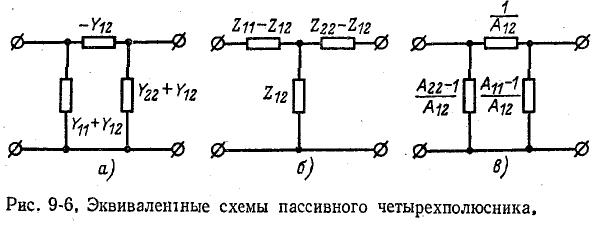
Пассивный П-образный четырехполюсник может быть преобразован в Т-образный (или наоборот) по правилу преобразования треугольника в эквивалентную звезду.
Следует заметить, что П-образ на я и Т-образная схемы замещения четырехполюсника не всегда физически реализуемы
Под физически реализуемой пассивной схемой понимается такая схема, в которой параметры r, L и С положительны. Если в какой-либо ветви схемы данное условие не выполнено, то схема физически нереализуема.
1 Это не относится к четырехполюсникам, не содержащим реактивных элементов.
Например, схема рис. 9-6, б нереализуема при отрицательном знаке действительной части 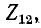
Схемой замещения четырехполюсника может служить и мостовая схема. Мостовая схема является физически реализуемым эквивалентом для любого реально осуществимого симметричного пассивного четырехполюсника.
Схемы замещения необратимых четырехполюсников, описанные выше, применяются для анализа и расчета электрических цепей, содержащих электронные лампы и транзисторы. К этому вопросу предстоит вернуться во второй части курса.
Пример 9-1.
Рассматривая автотрансформатор (см. рис. 8-21, о) как четырехполюсник, построить для него Т-образную схему замещения.
Выбрав положительные направления токов по третьему варианту и воспользовавшись параметрами Z, найдем:
На основании рис. 9-6, б получаются следующие сопротивления ветвей Т-образной схемы:
Полученный результат совпадает с данными (см, рис. 8-21, б).
Входное сопротивление четырехполюсника при произвольной нагрузке
Обозначим через 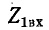
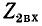
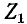
Следовательно, входное сопротивление 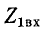
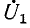
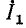
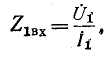
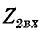
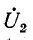
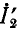
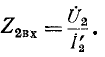
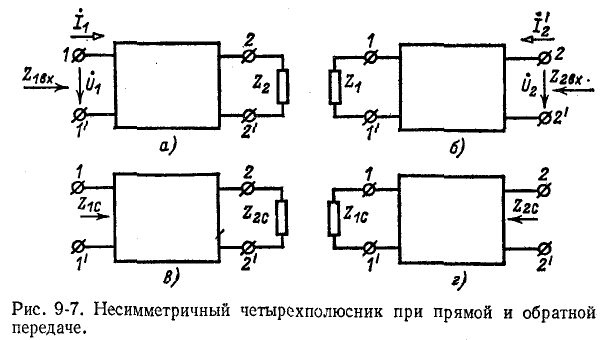
Входные сопротивления четырехполюсника могут быть выражены через любую систему коэффициентов четырехполюсника и комплексные сопротивления нагрузок 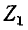
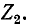
а и б — произвольная нагрузка: в и г — согласованная нагрузка.
Например, если воспользоваться системой уравнений (9-3), то, разделив первое из уравнений на второе, получим:
Аналогично при обратной передаче на основании (9-18)
Если воспользоваться таблицами приложений II и III, то можно выразить 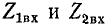
На практике применяются и другие выражения для 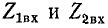
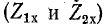
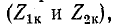
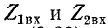
Рассмотренные выше функциональные зависимости 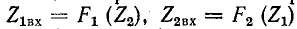
Характеристические параметры четырехполюсника
Положим, что сопротивления 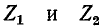
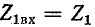
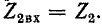
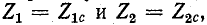
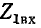
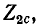
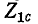
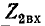
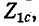
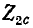
Такие два сопротивления называются характеристическими сопротивлениями несимметричного четырехполюсника.
Условие, когда четырехполюсник нагружен соответствующим характеристическим сопротивлением, называется условием согласованной нагрузки или согласованного включения.
Положив в (9-23) и (9-24)
и
получим
Совместное решение этих уравнений относительно 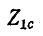
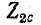
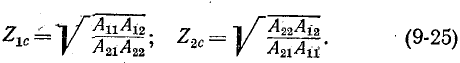
Введем для рассматриваемого обратимого четырехполюсника новый параметр g, удовлетворяющий условиям: 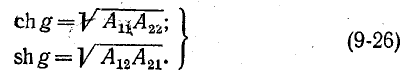
Эти условия всегда осуществимы, так как параметр g может быть комплексным. Кроме того, эти условия взаимно дополняют друг друга, так как имеющая место связь между коэффициентами (9-16) соответствует тригонометрической формуле
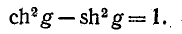
Параметр g в общем случае комплексный; 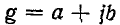
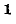
Физический смысл этих коэффициентов будет пояснен ниже. Выразим коэффициенты четырехполюсника формы 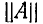
На основании (9-25):
Умножение (9-26) на (9-27) и (9-28) дает:
1 Иногда этот параметр называется коэффициентом передачи, его не следует смешивать с терминами «коэффициент передачи по напряжению» и «коэффициент передачи по току». В литературе ранее применялось обозначение
Деление (9-26) на (9-27) и (9-28) дает:
В результате подстановки (9-29)—(9-32) в (9-3) получаются уравнения несимметричного обратимого четырехполюсника в гиперболической форме, соответствующие положительным направлениям токов 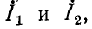
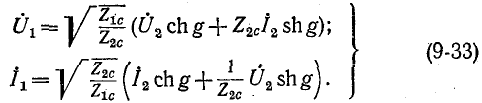
При согласованно подобранной нагрузке 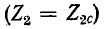
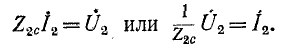
Если воспользоваться известным математическим соотношением
то уравнения (9-33) упростятся:
Отсюда следует, что при согласованно подобранной нагрузке модули напряжений и соответственно токов на входе и выходе четырехполюсника связаны уравнениями:
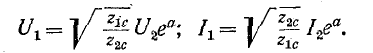
Множитель 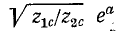
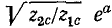
Если аргументы (углы) комплексных характеристических сопротивлений 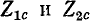
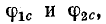
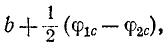
В общем случае коэффициент фазы b может быть определен как полусумма фазовых сдвигов между напряжениями и соответственно между токами на входе и выходе четырехполюсника, нагруженного согласованно. При равенстве углов 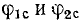
Характеристические параметры 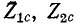
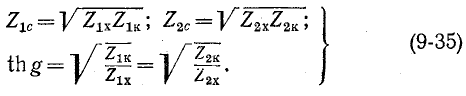
Подстановка (9-26) в формулу ch g + sh g = 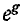
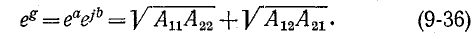
По этой формуле g вычисляется однозначно, если подставлять под радикалы коэффициенты А в показательной форме с последующим сложением углов и делением их суммы на 2. По формуле (9-35) для тангенса принципиально невозможно получить однозначное решение, так как входные сопротивления под радикалом не изменяются от перекрещивания выводов четырехполюсника. Поэтому формула (9-36) предпочтительнее формулы (9-35) для th g.
Вычисление g по формуле для th g ведется в следующем порядке:
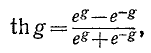
откуда 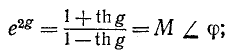
в результате логарифмирования
Следует отметить, что параметр g может быть также получен как половина натурального логарифма отношения произведений комплексных напряжения и тока на входе и выходе четырехполюсника при согласованной нагрузке.
Действительно, на основании (9-34) 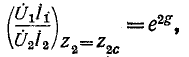
откуда 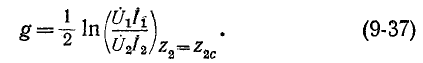
В случае симметричного четырехполюсника 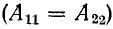
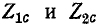
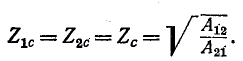
Следовательно, входное сопротивление симметричного четырехполюсника, нагруженного характеристическим сопротивлением 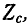
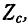
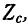
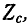
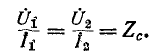
На основании (9-33) уравнения симметричного четырехполюсника при произвольной нагрузке записываются в гиперболической форме (для положительных направлений рис. 9-4) так:
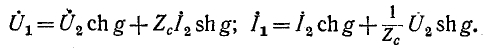
Если нагрузка подобрана согласованно, т. е. 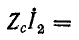
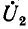
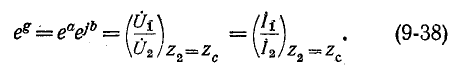
В этом случае амплитудные изменения напряжения и тока определяются множителем 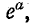
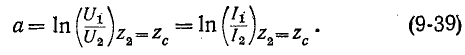
Величины g, а и b — безразмерные. Угол b вычисляется в радианах (рад); собственное затухание а, входящее в (9-39), принято вычислять в б е л а х (Б) или децибелах (дБ), которые определяются следующим образом.
Если полная мощность на выходе четырехполюсника в 10 раз меньше мощности на его входе, то затухание составляет 1-Б если мощность уменьшается в 100 раз, то затухание оценивается в 2 Б и т. д. Поэтому 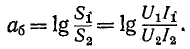
В случае согласованно нагруженного симметричного четырехполюсника
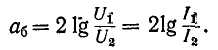
Децибел — единица затухания, в 10 раз мейьшая бела. Затухание 1 дБ соответствует уменьшению полной мощности в 1,26 раза или уменьшению напряжения и тока в 1,12 раза.
Затуханию 1 Нп соответствует уменьшение амплитуды и действующего значения напряжения или тока в е = 2,718 раза (так как при 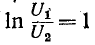
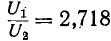
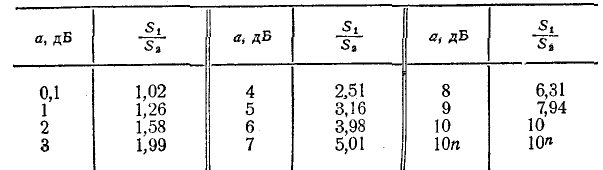
Табл. 9-1 иллюстрирует зависимость затухания в децибелах от отношений полных мощностей 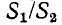
Таблица 9-1
Затухание при различных отношениях 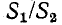
соответствующие им отношения величин напряжений или токов симметричного четырехполюсника, нагруженного согласованно, составляют
Для перехода от децибелов к неперам или обратно можно воспользоваться приведенным выше условием:
Вносимое затухание четырехполюсника
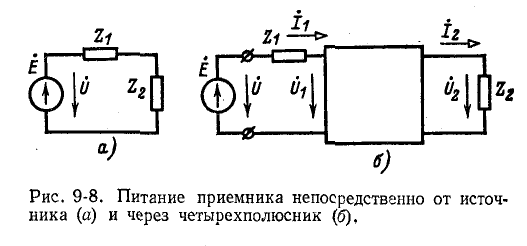
Вносимое затухание (или усиление) является мерой оценки изменения условий передачи при включении четырехполюсника между источником и приемником.
Положим, что между источником напряжения, имеющим внутреннее сопротивление 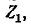
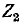
Под вносимым затуханием четырехполюсника подразумевается десятикратное значение десятичного логарифма (в децибелах) или половина натурального логарифма (в неперах) отношения полной мощности 5,. которую непосредственно отдавал бы источник сопротивлению 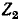
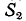
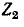

или 
Мощности 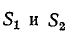
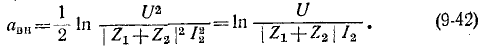
Отношение 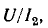
Пользуясь обозначениями рис. 9-8, б и уравнениями четырехполюсника, записанными в форме 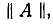
откуда 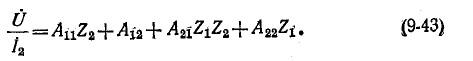
На основании (9-29) — (9-32)
Подстановка (9-44) в (9-43) дает:
После ряда алгебраических преобразований получается: 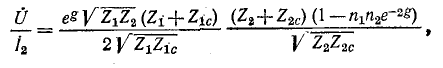
где
— так называемые коэффициенты отражения на входе и выходе четырехполюсника.
В связи с этим выражение (9-42) принимает следующий вид:
Следовательно, вносимое затухание состоит из пяти слагаемых. Первое слагаемое — собственное затухание четырехполюсника, второе — затухание вследствие несогласованности сопротивлений на входе четырехполюсника, третье — затухание вследствие несогласованности сопротивлений на выходе, четвертое — затухание вследствие взаимодействия несогласованностей на входе и выходе и пятое со знаком минус — затухание вследствие несогласованности сопротивлений источника и приемника.
Если вносимое затухание равно нулю, то это означает, что мощности на входе и выходе четырехполюсника равны между собой.
Когда четырехполюсник является усилителем мощности (например, в случае лампового триода или транзистора), выражения (9-40) и (9-41) дают отрицательные значения 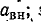
Передаточная функция
Передаточной функцией называется зависимость от частоты отношения комплексных амплитуд или комплексных действующих значений электрических величин 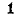
Передаточные функции, соответствующие отношению одноименных электрических величин, — коэффициент передачи по напряжению
и коэффициент передачи по току
представляют собой безразмерные, в общем случае комплексные, зависящие от частоты величины. Применительно к усилительным устройствам они носят название коэффициентов усиления по напряжению и току.
Отношения разноименных электрических величин — передаточное сопротивление 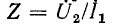
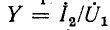
Зависимости модулей комплексных отношений представляют собой амплитудно-частотные, зависимости их аргументов — фазо-частотные характеристики четырехполюсника. 
Эти характеристики имеют важное значение для работы устройств автоматики и радиотехники.
В общем случае четырехполюсника, нагруженного произвольным сопротивлением 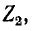
Через коэффициенты формы 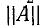
Н
При холостом ходе и коротком замыкании эти коэффициенты примут вид: 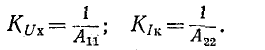
В случае обратной передачи, очевидно, можно написать
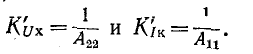
Отсюда видно, что для обратимого четырехполюсника коэффициент передачи по напряжению при холостом ходе и прямом направлении передачи энергии равен коэффициенту передачи по току при коротком замыкании и обратном направлении передачи энергии. В свою очередь коэффициент передачи по току при коротком замыкании и прямом направлении передачи равен коэффициенту передачи по напряжению при холостом ходе и обратном направлении передачи.
Каскадное соединение четырехполюсников, основанное на согласовании характеристических сопротивлений
На практике широко распространено каскадное или цепочечное соединение четырехполюсников, при котором входные выводы каждого последующего четырехполюсника присоединяются к выходным выводам предыдущего четырехполюсника; цепи, служащие для передачи электрической энергии (каналы связи и т. д.) обычно состоят из звеньев, следующих друг за другом.
Каскадное соединение четырехполюсников, выполненное по принципу согласования характеристических сопротивлений, заключается в том, что входное сопротивление на выводах любого четырехполюсника равно характеристическому.
Рисунок 9-9 иллюстрирует каскадное соединение двух четырехполюсников. Ввиду того что комплексное сопротивление нагрузки согласовано с выходным характеристическим сопротивлением 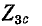
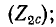
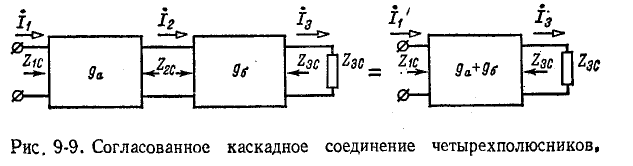
Отсюда следует, что каскадно соединенные четырехполюсники с согласованными характеристическими сопротивлениями могут быть замещены одним четырехполюсником, имеющим характеристические сопротивления, равные входному характеристическому сопротивлению первого и выходному характеристическому сопротивлению последнего четырехполюсников (рис. 9-9). Мера передачи g результирующего четырехполюсника определяется алгебраической суммой мер передачи составных четырехполюсников.
В самом деле, применительно к схеме рис. 9-9 в соответствии с (9-34)
Полученные выражения подтверждают сказанное выше: результирующий четырехполюсник имеет характеристические сопротивления 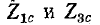
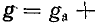
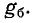
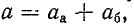
Было показано что передача максимума активной мощности обеспечивается, когда комплексные сопротивления источника и нагрузки являются сопряженными. Это условие не выполняется в случае согласования характеристических сопротивлений каскада в прямом и обратном направлениях, если характеристические сопротивления комплексные. Однако если они активные (включая сопротивление источника), как это нередко имеет место на практике, то обеспечивается оптимальное условие передачи мощности.
Согласование характеристических сопротивлений .широко применяется в автоматике, приборостроении и электронике.
Уравнения сложных четырехполюсников в матричной форме
Для получения параметров результирующего четырехполюсника, составленного из более простых четырехполюсников, параметры которых известны, удобно пользоваться матричной записью,
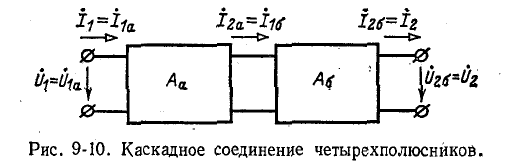
В зависимости от схемы соединения сложного четырехполюсника применяется та или иная форма уравнений, а именно:
- при каскадном соединении (рис. 9-10) —форма
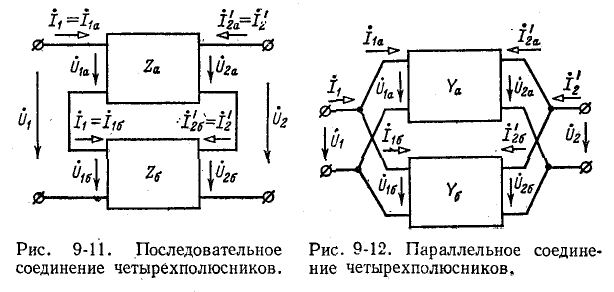
- при последовательном соединении (см. рис. 9-11) — форма
- при параллельном соединении (см. рис. 9-12) — форма
Каскадное соединение четырехполюсников (рис. 9-10). Уравнения
составных четырехполюсников в матричной форме
Здесь индексом а отмечены величины, относящиеся к первому четырехполюснику, а индексом 6 — величины, относящиеся ко второму четырехполюснику.
При каскадном соединении
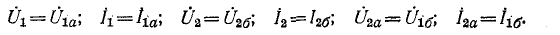
Следовательно,
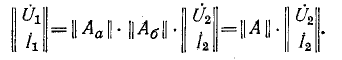
Таким образом, матрица 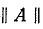
Эго правило распространяется на случай каскадного соединения любого числа четырехполюсника.’ При этом матрицы, подлежащие
перемножению, записываются в порядке следования соответствующих четырехполюсников, так как умножение матриц не подчиняется переместительному закону.
Последовательное соединение четырехполюсников (рис. 9-11) Уравнения составных четырехполюсников в матричной форме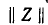
Таким образом, матрица 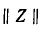
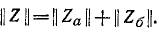
Параллельное соединение четырехполюсника (рис. 9-12)
Уравнения составных четырехполюсников в матричной форме 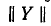
При параллельном соединении четырехполюсников:
При параллельном соединении четырехполюсников:
Таким образом, матрица 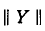
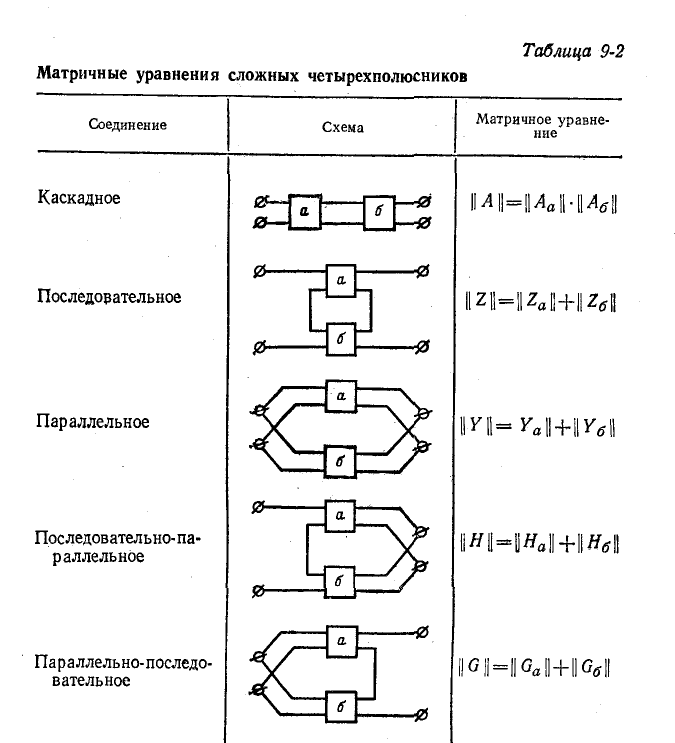
Правила нахождения матриц сложных четырехполюсников сведены в табл. 9-2. Они справедливы при любом числе составных четырехполюсников. Однако правила сложения матриц применимы только при равенстве токов входящего и выходящего в каждой паре выводов составных четырехполюсников, которое должно быть обеспечено тем или иным способом.
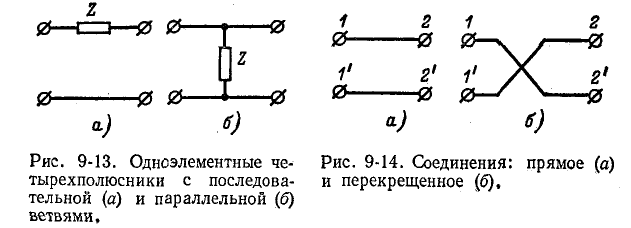
Одноэлементные четырехполюсники
Простейшими четырехполюсниками являются одноэлементные четырехполюсники, состоящие из последовательного (рис. 9-13, а) или параллельного (рис. 9-13, б) двухполюсника.
Уравнения первого из них в форме 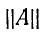
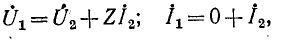
или, что то же, 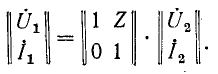
Уравнения одноэлементного четырехполюсника с параллельной ветвью (рис. 9-13, б) в форме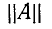
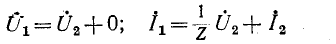
или, что то же,
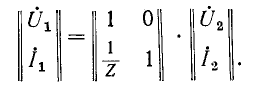
Если в первом четырехполюснике (рис. 9-13, а) положить Z = 0 или, что то же, во втором четырехполюснике (рис. 9-13, б) принять 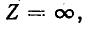
в форме
соответствующее непосредственному прямому соединению, показанному на рис. 9-14, а.

Поэтому при перекрещивании входных или выходных выводов любого четырехполюсника его матрица 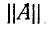
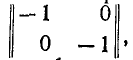
Г-образный четырехполюсник
Коэффициенты Г-образного четырехполюсника (см. рис. 9-15) могут быть получены непосредственно по формулам. Например, для схемы рис. 9-15, а коэффициенты формы ||Л|| согласно формулам будут:
Легко убедиться, что перекрещенному соединению (рис. 9-14, б) соответствует уравнение в форме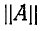
Аналогично могут быть вычислены и другие коэффициенты.
Характеристические параметры Г-образного четырехполюсника могут быть вычислены по формулам (9-25) и (9-26).
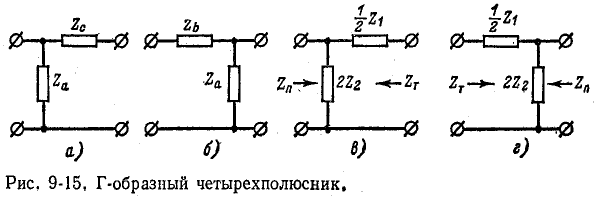
Для схемы рис. 9-15, а:
Для схемы рис. 9-15, б:
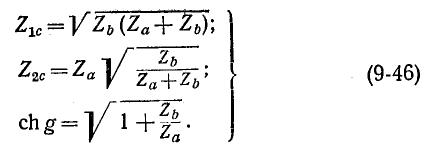
При расчете электрических фильтров и в ряде других случаев за исходные схемы Г-образных четырехполюсников принимаются схемы рис. 9-15, виг, причем мера передачи Г-образного четырехполюсника обозначается через g/2, для того чтобы при согласованном каскадном соединении двух таких четырехполюсников получался Т- или П-образный четырехполюсник с мерой передачи g. При этом характеристическое сопротивление со стороны параллельной ветви обозначается через 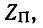
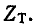
На основании (9-45) или (9-46):
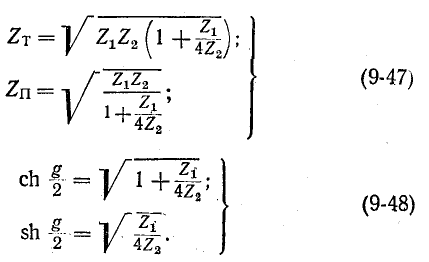
Эти выражения используются в теории электрических фильтров.
Т-образный и П-образный четырехполюсники
Рассматривались схемы замещения четырехполюсника и приводились схемы Т-образного и П-образного четырехполюсников. Коэффициенты таких четырехполюсников вычисляются по общей методике.
Так, для Т-образной схемы рис.
9-16 получим:
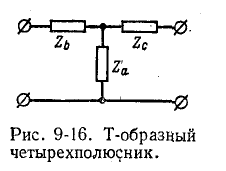
Характеристические параметры находятся по формулам (9-25) и (9-26).
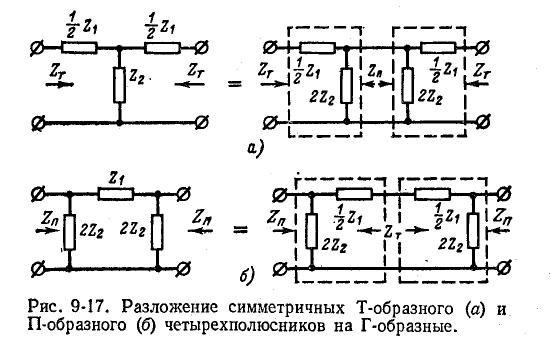
Симметричные Т- и П-образные четырехполюсники можно получить согласованным каскадным соединением двух одинаковых Г-образных четырехполюсников (рис. 9-17, а и б). Результирующие четырехполюсники имеют характеристические сопротивления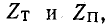
С учетом (9-48) имеем:
Тот же результат получается на основании (9-26).
Симметричный мостовой четырехполюсник
Для симметричного мостового четырехполюсника (см.рис. 9-18) в соответствии с можно получить коэффициенты формы
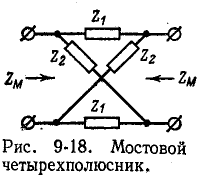
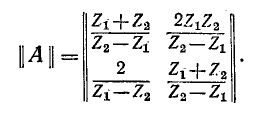
Характеристические параметры симметричного мостового четырехполюсника находятся по формулам:
Как уже отмечалось, мостовой четырехполюсник является физически реализуемым эквивалентом для любого реально осуществимого симметричного пассивного четырехполюсника.
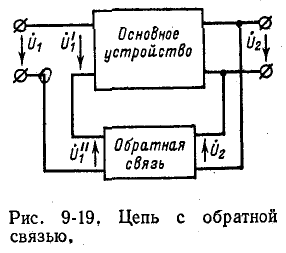
Обратная связь
Последовательно-параллельное соединение двух четырехполюсников представляет собой один из основных видов цепи с обратной связью, в которой напряжение на выходе воздействует на входные напряжения системы. Пусть некоторое устройство, которое назовем основным, представляет собой четырехполюсник с передаточной функцией
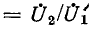
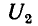
Обозначим передаточную функцию устройства обратной связи через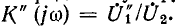
Следовательно, передаточная функция всей системы
или, если разделить числитель и знаменатель на

Если поменять полярность одной из пар выводов устройства обратной связи, то в знаменателе (9-51) вместо знака минус получится знак плюс.
Обратная связь, при которой напряжение, пропорциональное выходному напряжению, добавляется к входному напряжению системы так, что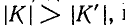
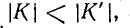
Выражение (9-51) может быть переписано так:
Если 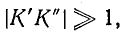
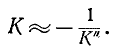
Это выражение показывает, что передаточная функция системы зависит от передаточной функции устройства обратной связи. Регулируя последнюю, можно воздействовать на передаточную функцию всей системы.
Видео:Теоретические основы электротехники 53. Четырёхполюсники. Нахождение сопротивлений схем замещенияСкачать

Методы расчета электрических цепей с использованием теории четырехполюсников
Основные теоретические сведения:
В радиотехнике обычно интересуются прохождением сигналов через произвольную сложную электрическую цепь. При этом важно установить связь между выходными и входными значениями сигнала, не рассчитывая токи и напряжения на элементах внутри цепи.
Для такого анализа цепь (или часть цепи) представляется обобщенной схемой в виде четырехполюсника. Анализ цепи в этом случае производится на основе классической теории четырехполюсников, которая устанавливает связь между токами и напряжениями, действующими на входных и выходных зажимах (полюсах).
Краткая характеристика четырехполюсников
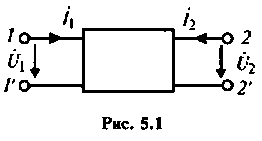
На рис. 5.1. показан неавтономный активный четырехполюсник. В зависимости от того, какая пара переменных величин считается независимой, процессы в четырехполюсниках можно описать одной из шести форм уравнений, приведенных и табл. 5.1.
Коэффициенты уравнений характеризуют свойства четырехполюсника, зависящие только от схемы цепи и параметров ее элементов. Поэтому коэффициенты уравнения называют собственными (иногда первичными) параметрами четырехполюсника. Их можно определить экспериментально или аналитически по известной схеме цепи. Для определения параметров применяют режим холостого хода (XX) или режим короткого замыкания (КЗ) на соответствующих зажимах четырехполюсника.
Режим работы четырехполюсника выбирают так, чтобы одно из слагаемых данных уравнений (табл. 5.1) было равно нулю. Например, для выходных зажимов при XX 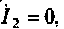
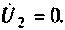
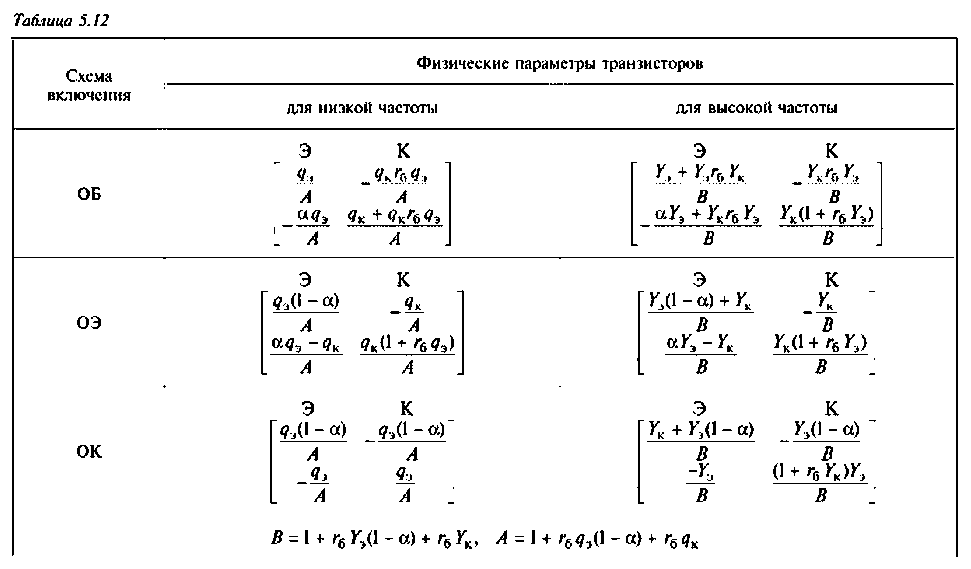
При выбранном режиме работы четырехполюсника каждый коэффициент уравнений имеет конкретный физический смысл. Например, из уравнений в форме Y (табл. 5.1) видно, что каждый коэффициент равен отношению тока к напряжению. Поэтому по физическому смыслу Y-параметры являются входными или передаточными проводимостями. В этом смысле Z- параметры являются входными или передаточными сопротивлениями.
А- и В-параметры называют передаточными, так как по физическому смыслу они являются передаточными сопротивлениями (проводимостями) или коэффициентами передачи по напряжению (току). Параметры вида Н и G называются гибридными, так как они содержат входные сопротивления (проводимости) и коэффициенты передачи по напряжению (току).
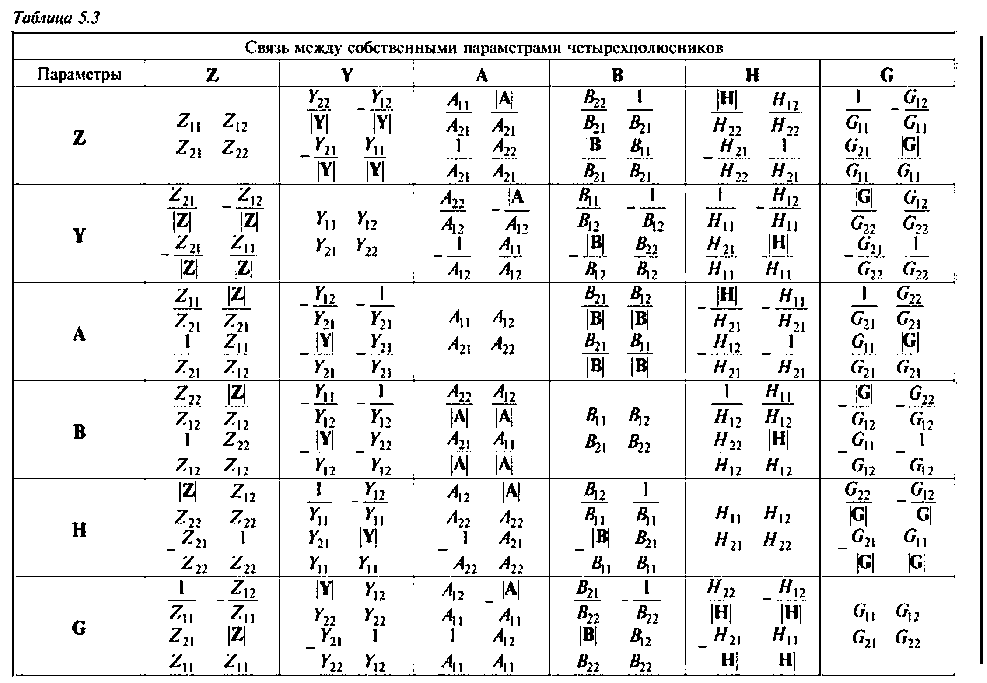
В общем случае четырехполюсник характеризуется четырьмя параметрами. Для взаимных и симметричных четырехполюсников число параметров уменьшается, так как могут быть два параметра, равных по величине. Условия взаимности и симметричности четырехполюсников для различных собственных параметров приведены в табл. 5.2.
Любая система параметров может быть выражена через каждую из других пяти систем (табл.5.3). Например, в справочнике приведены Н-параметры транзистора, а для расчета цепи необходимо знать Y-параметры транзистора. В этом случае необходимо воспользоваться формулами, расположенными на пересечении строки Y и столбца Н (табл. 5.3):
где Н — определитель матрицы Н-параметров.
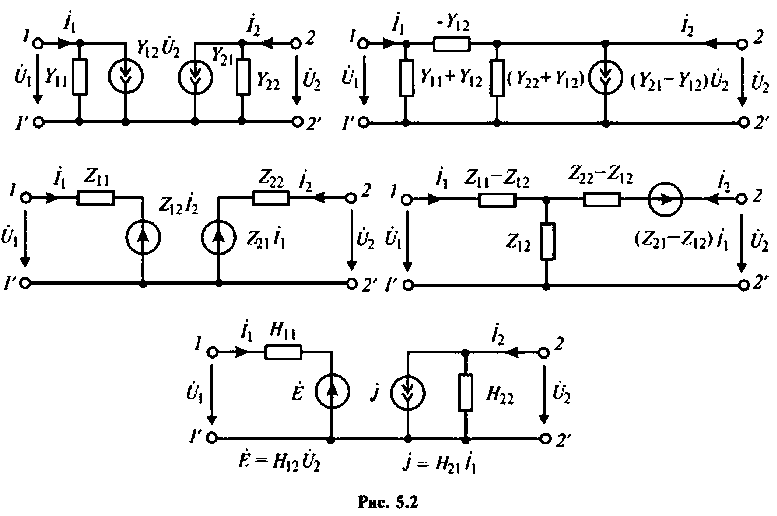
Использование собственных параметров четырехполюсника позволяет при расчете любую электрическую цепь представить эквивалентной схемой замещения.
На рис. 5.2 показаны схемы замещения на базе Y-, Z- и Н-параметров. Наиболее часто схемы замещения применяют для описания электрических приборов (триодов, транзисторов), включенных в электрическую цепь.
Собственные параметры четырехполюсника не учитывают влияние внешних цепей (источника и нагрузки). Для расчета четырехполюсника с учетом этих целей применяют комплексные функции, которые иногда называют вторичными или рабочими параметрами. Эти параметры выражают через собственные параметры Y или Z.
Если источник задан напряжением или током на входе четырехполюсника, то при расчете необходимо учитывать только нагрузку. Комплексные входные и передаточные функции для этого случая приведены соответственно в табл. 5,4 и 5.5.
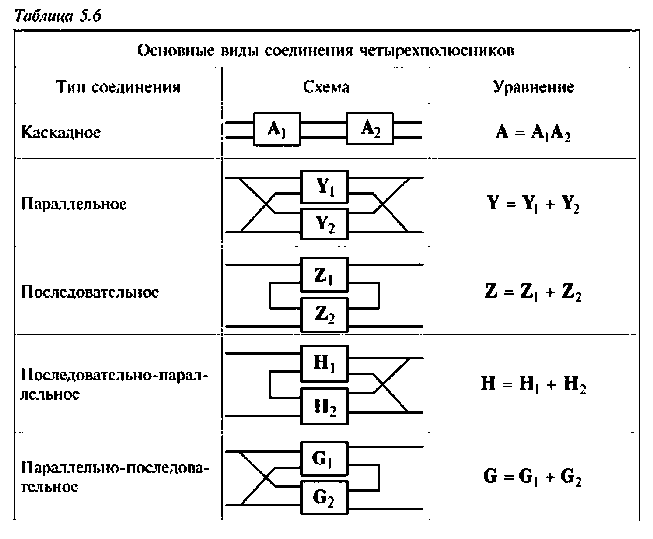
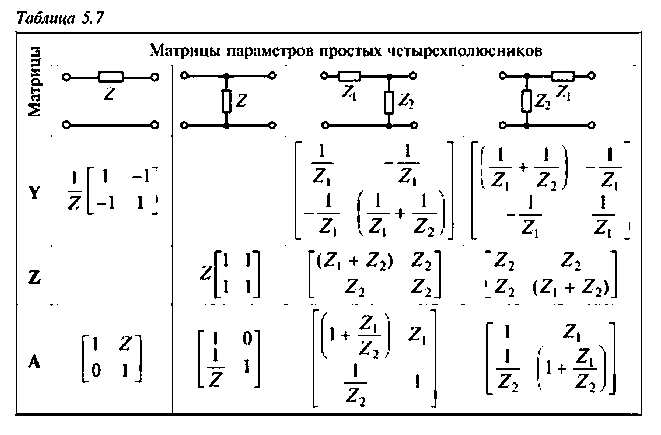
Расчет в ряде случаев удается упростить, если цепь представить в виде сложного четырехполюсника. Основные виды соединения двух простых четырехполюсников показаны в табл. 5.6. Матрицы параметров некоторых простых четырехполюсников приведены в табл. 5.7 и 5.8.
Примеры решения задач:
Пример 5.1.1.
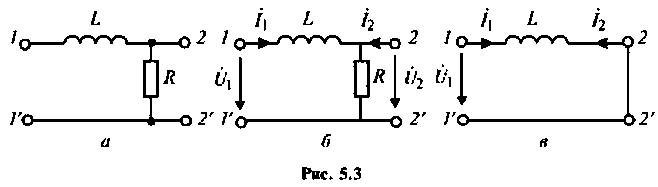
Для четырехполюсника (рис. 5.3, а) определить А-параметры. Y- и Z-параметры найти по связям с полученными параметрами.
Дано:
Решение
1. Строим схемы для холостого хода и короткою замыкания на зажимах 2—2′ (рис. 5.3, б, в).
Для режима холостого хода 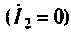
Отсюда 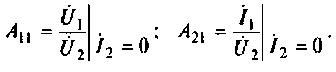
Для определении 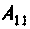
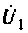
При расчете 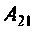
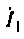
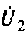
Для режима короткого замыкания 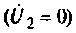
Для определения 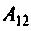
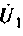
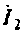
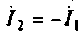
Подставляя по значение в исходную формулу, получаем
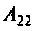
т.е.
2. Рассчитаем Y- и Z-параметры по формулам связи с А-параметрами (см. табл. 5.3):
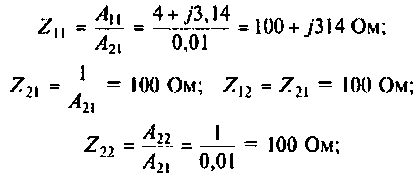
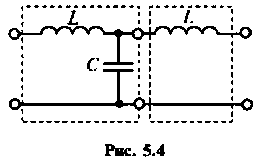
Пример 5.1.2.
Найти матрицу А низкочастотного фильтра, изображенного на рис. 5.4, пользуясь матрицами элементарных четырехполюсников.
Решение
1. Определяем матрицу 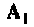
2. Находим матрицу 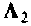
3.Рассчитаем матрицу А сложного четырехполюсника при каскадном включении элементарных четырехполюсников
Пример 5.1.3.
Определить комплексную передаточную функцию по напряжению реактивного фильтра нижних частот (см. рис. 5.4), нагруженного на активное сопротивление 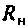
Решение
1. Рассчитаем Y-параметры ненагруженного четырехполюсника. Из табл. 5.8 определим
2.Комплексную передаточную функцию по напряжению нагруженного четырехполюсника определим по формуле (см. табл. 5.5).
Учитывая, что 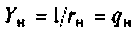
Видео:19-1 Схема замещения асинхронного двигателя, механическая характеристикаСкачать

Методы расчета линейных активных цепей с использованием теории четырехполюсников
Основные теоретические сведения:
Цепи с электронными приборами (электронными лампами, транзисторами, операционными усилителями и т.п.), способные в определенных режимах усиливать по мощности входной сигнал, называются активными. Вследствие нелинейности вольт-амперных характеристик (ВАХ) электронных приборов такие цепи, строго говоря, являются нелинейными. Если амплитуда входного сигнала мала, а рабочая точка выбрана на линейном участке ВАХ прибора, id активные цели можно рассматривать как линейные.
В этом случае их анализ производят методами теории линейных электрорадиоцепей.
Для расчета линейных электрических цепей активные элементы заменяют их моделями, которые с определенной степенью точности отражают происходящие в них физические процессы. Paзличают математические (аналитические) и электрические модели электронных приборов. При расчете линейных активных цепей (ЛАЦ) известными методами теории цепей используют электрические модели, т. е. эквивалентные электрические схемы активных элементов. Обычно применяют два вида эквивалентных схем электронных приборов — физическую и схему на базе собственных параметров четырехполюсника.
Физическая эквивалентная схема строится на основе структуры прибора и принципа его работы, т. е. на основе так называемых физических параметром.
Рассмотрим эквивалентные схемы трех основных видов электронных приборов, применяемых для усиления сигналов. Способность прибора усиливать сигнал отражается включением в эквивалентную схему зависимого источника тока или напряжения.
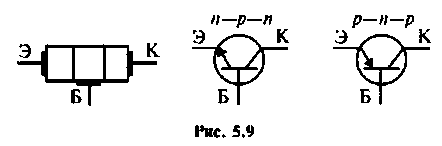
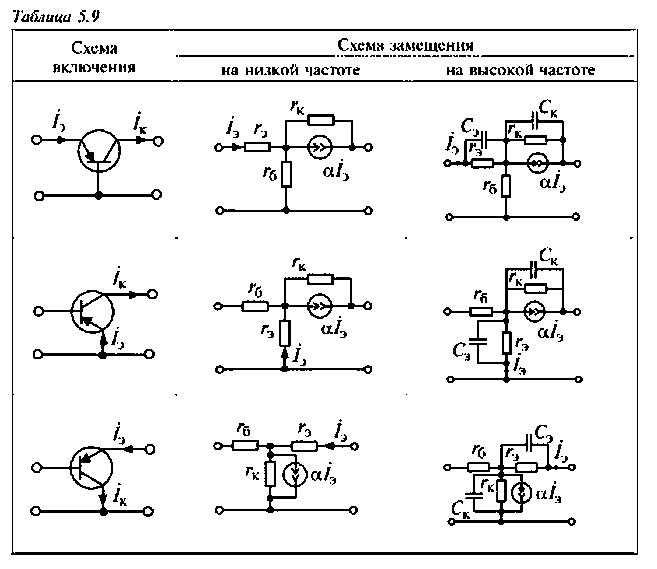
На рис.5.9 схематически показано устройство плоскостного биполярного транзистора и его условное графическое изображение. В электрическую цепь транзистор может быть включен по схеме с обшей базой (ОБ), но схеме с общим эмиттером (ОЭ) или по схеме с общим коллектором (ОК). В табл. 5.9 приведены физические эквивалентные схемы биполярного транзистора для трех схем включения.
Элемент 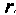
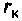
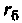
В общем случае все физические параметры являются частотно-зависимыми. Этот факт учитывается включением в электрическую модель емкостей эмиттера и коллектора. Эти емкости достаточно малы, поэтому их влияние необходимо учитывать лишь на высоких частотах. Наиболее вредной является емкость коллектора шунтирующая источник.
В рассматриваемых схемах усилительные свойства отображены зависимыми источниками тока в цепи коллектора, которые выражены через коэффициент передачи тока;
Зависимый источник можно выразить также через коэффициент 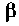
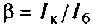
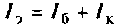
В современных транзисторах ток базы мал по сравнению с током эмиттера. Обычно 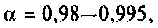
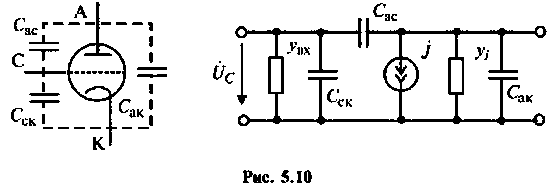
На рис.5.10 приведены условное графическое изображение и физическая эквивалентная схема электровакуумного триода.
Эквивалентная схема характеризуется физическими параметрами: входным и внутренним 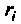
Величины входного и внутреннего сопротивлений зависит от режима работы триода. Обычно на сетку подается отрицательное относительно катода напряжение. При этом ток сетки близок к нулю, а входное сопротивление велико — единицы — десятки мегаом. Внутреннее сопротивление триода при работе в линейном режиме обычно лежит в пределах от 10 до 30 кОм.
Зависимый источник тока в эквивалентной схеме определяется крутизной S вольт-амперной характеристики и напряжением 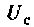
где 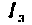
Важным параметром триода является коэффициент усиления
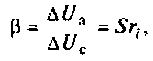
где 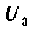
Современные триоды имеют коэффициент усиления от 3 до 100 и крутизну от 1 до 50 мА/В.
Рассмотренная физическая эквивалентная схема соответствует включению триода и цепь по наиболее распространенной схеме с общим катодом. Кроме того, триод может включаться в цепь по схеме с общим анодом или с обшей сеткой.
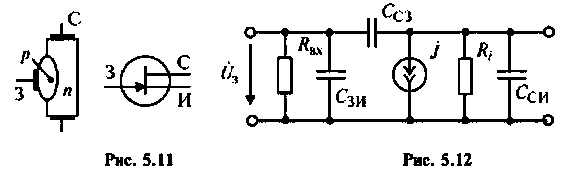
Полевой (униполярный, канальный) транзистор является полупроводниковым аналогом электровакуумного триода. На рис.5.11 схематически показано устройство полевого транзистора с управляющим 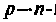
Сетке триода соответствует затвор (3) транзистора, катоду -исток (И), аноду — сток (С).
Физическая эквивалентная схема этого транзистора, включенного на схеме с общим истоком, показана на рис. 5.12. Видно, что эта схема аналогична схеме триода. Зависимый источник тока характеризуется крутизной ВАХ и напряжением 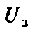
где 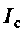
Величина внутреннего сопротивления может достигать сотен килоом.
Второй тип эквивалентных схем электронных приборов основан на представлении их линейными невзаимными четырехполюсниками. В этом случае параметрами активных элементов являются коэффициенты уравнений четырехполюсников (см. табл. 5.1). Поэтому эквивалентными схемами электронных приборов являются схемы замещения четырехполюсников на базе соответствующих параметров (см. рис. 5.2). Аналогично физическим эквивалентным схемам усилительные свойства электронных приборов отражаются зависимыми источниками.
В настоящее время основными параметрами транзисторов считаются гибридные Н-параметры, так как они наиболее просто измеряются. Именно эти параметры приводятся во всех справочниках. При расчете некоторых цепей удобнее применять Y-napaметры. Переход от одних параметров к другим производится по известным формулам связи собственных параметров четырехполюсников разных систем (см. табл. 5.3).
Н- и Y-параметры называются низкочастотными мало сигнальными, так как они справедливы лишь на низких частотах и для входных сигналом с малыми амплитудами. При работе электронных приборов на низких частотах все их параметры являются вещественными.
Параметры электронных приборов как четырехполюсников, в отличие от физических параметров, существенно зависят от схемы включения прибора в цепь. Поэтому к цифровому индексу параметра добавляют соответствующую букву.
Например, матрицы Н-параметров транзисторов, включенных по схеме с ОЭ и по схеме с ОБ, соответственно имеют вид:
Аналогично записываются матрицы Y-параметров.
Зная параметры прибора для одной схемы включения, можно найти его параметры для другой схемы. В табл. 5.10 приведены формулы, связывающие 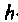
Н-параметры так же, как и Y-параметры, непосредственно связаны с физическими параметрами электронного прибора. Некоторые формулы, определяющие эту связь для биполярных транзисторов, приведены в табл. 5.11 и 5.12.
Отметим физический смысл Н-параметров транзистора, который следует из уравнений четырехполюсника в форме Н (см. табл. 5.1).
В систему Н-параметров входят величины:
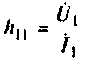
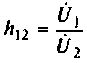
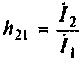
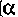
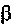
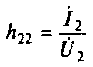
По физическому смыслу выходная проводимость есть внутренняя проводимость транзистора;
Для полевого транзистора или электровакуумного триода эквивалентную схему можно упростить. Наиболее часто эти приборы включают в цепь по схеме с общим катодом (истоком). При этом входное сопротивление велико, поэтому ток сетки (затвора) близок к нулю.
Из уравнений в форме 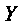
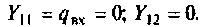
Расчет линейных активных целей (ЛАЦ) с использованием рассмотренных эквивалентных схем активных элементов может производиться по известным методам. В настоящее время наиболее часто применяют MУH, MKT, метод сигнальных графов.
Введение в эквивалентные схемы активных элементов зависимых (управляемых) источников позволяет исключить из расчета независимые источники цепи (источники питания), которые обеспечивают заданный режим работы. При этом зависимые источники работают на частоте сигнала, подаваемого на вход цепи.
Таким образом, при расчете полагают, что в цепи действует один независимый источник сигнала на входе. Поэтому расчет цепи проводят обычным способом, определяя заданные токи (напряжения) или комплексные функции.
Особенность расчета ЛАЦ по MKT или МУН состоит в следующем. Электрическая схема цепи заменяется эквивалентной схемой, в которой активные элементы заменяются физическими эквивалентными схемами или схемами на базе параметров четырехполюсника. Далее, в соответствии с выбранным методом расчета составляются по общим правилам контурные или узловые уравнения.
Например, допустим, что схема имеет три независимых контура. Источник сигнала 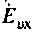
В этом случае матрица контурных сопротивлений описывает только пассивные элементы цепи. Условимся называть такие матрицы матрицами пассивной части цепи и обозначим соответственно 
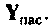
Зависимые источники активных элементов неизвестны, они определяются токами (напряжениями) в цепи. Поэтому их необходимо выразить через контурные токи (при MKT) или через узловые напряжения (при МУН) и перенести в соответствующие элементы правой части уравнений.
После преобразований все уравнения, кроме первого, будут иметь нулевые правые части. При этом матрица Z или Y характеризует цепь с учетом активных элементов. Такую матрицу будем называть полной.
Так как электронной прибор является невзаимным (однонаправленным), то полная матрица будет несимметричной, т. е. в общем случае
Полная матрица Z или Y позволяет но известным формулам через определители рассчитать любую комплексную функцию цепи.
Эти методы расчета обычно называют методами эквивалентных схем. Они отличаются наглядностью, простатой и логичностью действий, позволяют использовать любые эквивалентные схемы активных элементов. Однако их применение ограничено, так как для сложных многокаскадных цепей метод становится громоздким.
Представление зависимых источников через искомые точки или напряжения, перенос этих величин в левые части уравнений имеют общие закономерности. Исследования этих закономерностей позволило обобщить (формализовать) методы расчета. Суть обобщения состоит в том, что можно по известным правилам составлять полную матрицу сопротивлений (проводимостей) цепи, не составляя систему уравнений.
Рассмотрим обобщенный метод узловых напряжений (ОМУН). Сущность этого метода состоит в следующем. Электронные приборы в схеме заменяют физической эквивалентной схемой, затем по известным правилам определяют независимые узлы и для них составляют матрицу 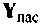
Управляющим параметрам называют коэффициент (по модулю) при узловом напряжении, которое создает ток зависимого источника активного элемента. Он рассчитывается непосредственно из выражения для зависимого источника тока.
Для биполярного транзистора 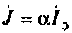
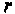
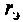
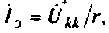
Проводимость 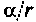
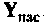
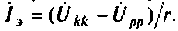
Номера строк этих элементов определяются номерами узлов цепи, к которым подключен зависимый источник тока 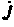
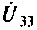
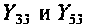
Параметр вписывают со знаком плюс, если источник и напряжение относительно своих углов направлены одинаково. Например, в элемент параметр необходимо вписать со знаком плюс, если ток источника направлен к узлу 5, а напряжение 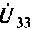
Необходимо помнить, что при определении направления напряжения 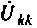
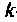
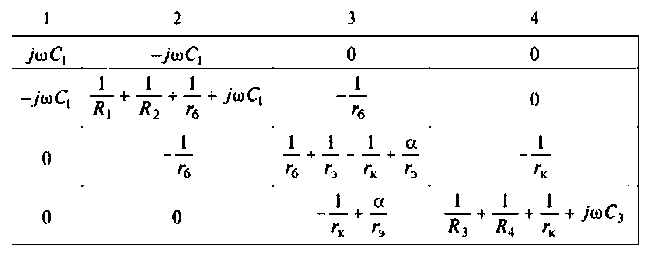
Для расчета ЛАЦ применяют также другой вариант ОМУН, принципиально отличающийся от рассмотренного выше. Сущность этого метода состоит в следующем. Для расчета составляют эквивалентную схему цепи, из которой исключают все активные элементы. Точки включения электродов этих элементов на схеме считаются узлами. Для этой схемы по известным правилам МУН составляют матрицу
Электронные приборы описывают матрицами Y-параметров. Для получения полной матрицы цепи элементы матрицы Y-napaметров необходимо вписать в одноименные элементы матрицы 
Если электронный прибор включен в цепь определенно, т. е. по схеме с общим электродом, то он характеризуется четырьмя параметрами, например:
В общем случае электронный прибор включается в цепь неопределенно, т. е. без общего электрода. При этом на всех электродах имеется напряжение относительно базисного узла (относительно земли).
Пример неопределенного включения транзистора показан на рис. 5.13. В этом случае транзистор описывается не четырьмя, а девятью Y-параметрами. Такая матрица формируется на основе параметров транзистора с определенной схемой включения. Для схемы, прицеленной на рис. 5.13, матрица Y-параметров транзистора имеет вид:
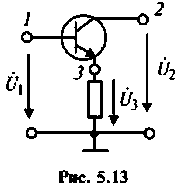
Можно показать, что такая матрица является неопределенной, т. е. суммы ее элементов в каждой строке и в каждом столбце тождественно равны нулю. На основании этого свойства определяют дополнительные параметры. Например: 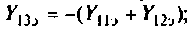
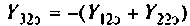
Чтобы получить правильную полную матрицу проводимостей ЛАЦ, необходимо знать правила вписывания Y-параметров электронных приборов. Если, например, электроды транзистора включены к узлам с номерами 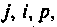
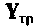
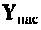
Примеры решения задач:
Пример 5.2.1.
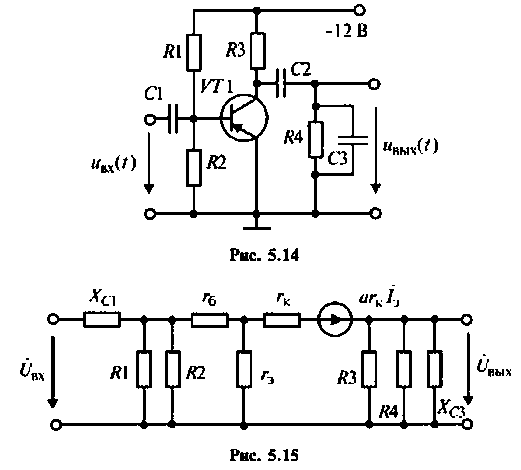
Рассчитать комплексный коэффициент передачи по напряжению однокаскадного транзисторного усилителя (рис. 5.14) методом контурных токов (MKT). Транзистор представить физической схемой замещения.
Решение
1. Составим эквивалентную схему транзисторного усилителя по переменному току (рис. 5.15).
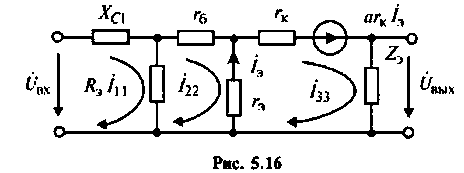
2. Выполним эквивалентные преобразования сопротивлений в схеме (рис. 5.16).
3. Выберем независимые контуры и зададим положительное направление контурных токов в них (рис. 5.16).
4. Составим систему уравнении по MKT:
5. Выразим ток эмиттеpa через контурный ток
6. Подставим ток эмиттера в уравнения
7. Сгруппируем подобные слагаемые в уравнениях
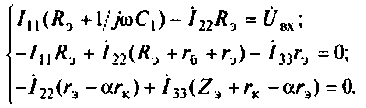
8. Рассчитаем ток 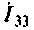
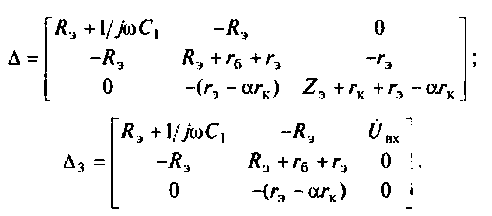
9. Рассчитаем выходное напряжение транзисторного усилителя
10. Рассчитаем комплексный коэффициент передачи по напряжению транзисторного усилителя
Пример 5.2.2.
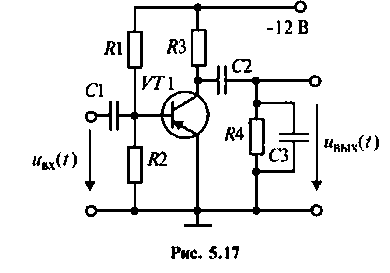
Рассчитать комплексный коэффициент передачи по напряжению однокаскадного транзисторного усилителя (рис. 5.17) MKT. Транзистор представить схемой замещения на базе Н-параметров.
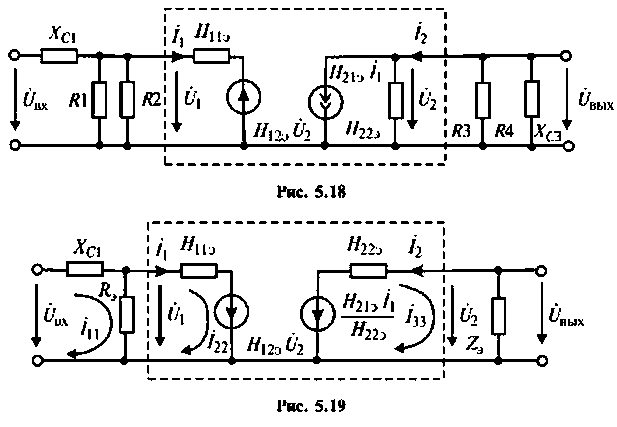
1. Составим эквивалентную комплексную схему транзисторного усилителя по переменному току (рис. 5.18).
2.Выполним эквивалентные преобразования сопротивлений в схеме и преобразуем источник тока в эквивалентный источник ЭДС (рис. 5.19):
3. Выберем независимые контуры и зададим положительное направление в них контурных токов.
4. Составим систему уравнений по MKT:
5. Выразим ток 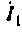
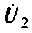
6. Подставим их выражения в уравнения:
7. Сгруппируем подобные слагаемые в уравнениях:
8. Рассчитаем комплексный ток третьего контура
9. Рассчитаем выходное напряжение транзисторного усилителя
10. Рассчитаем комплексный коэффициент передачи по напряжению транзисторного усилителя
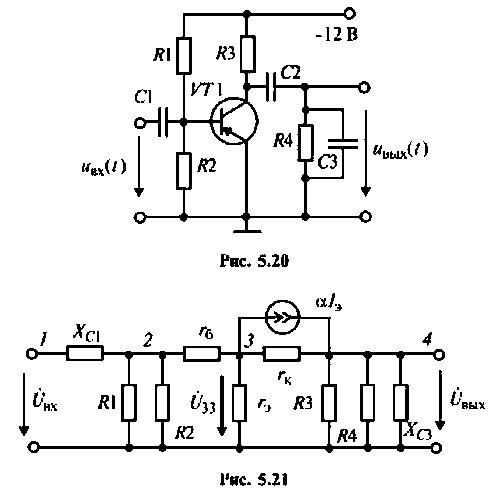
Пример 5.2.3. Рассчитать комплексный коэффициент передачи по напряжению однокаскадного транзисторного усилителя (рис. 5.20) ОМУН. Транзистор представить физической схемой замешения.
Решение
1. Составим эквивалентную комплексную схему транзисторного усилителя по переменному току (рис. 5.21).
2. Выберем независимые углы и зададим положительное направление узловых напряжений.
3. Составим матрицу проводимостей пассивной части схемы.
4. Определим управляющий параметр. Из схемы видно, что 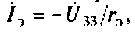
Отсюда получим управляющий параметр:
5. Впишем управляющий параметр в матрицу
Источник тока включен в узлы 3 и 4, а управляется он узловым напряжением третьего узла 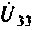
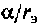
Ток источника направлен от yзла 3, а напряжение 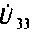
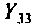
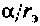
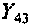
6. Рассчитаем комплексный коэффициент передачи усилителя по формуле (см. табл. 4.1)
где 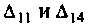
Пример 5.2.4.
Рассчитать Y-параметры транзистора 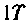
Дано:
Решение
1. Рассчитаем параметр 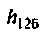
2. Рассчитаем 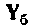
3. Используя основное свойство неопределенной матрицы, составим матрицу Y-параметров транзистора
4. Составим матрицу 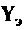
Пример 5.2.5.
Рассчитать комплексный коэффициент передачи по напряжению однокаскадного транзисторного усилителя (см. рис. 5.20) ОМУН. Транзистор описать матрицей Y-параметров.
Решение
1.Составим эквивалентную комплексную схему однокаскадного транзисторного усилителя без учета транзистора (рис. 5.22). 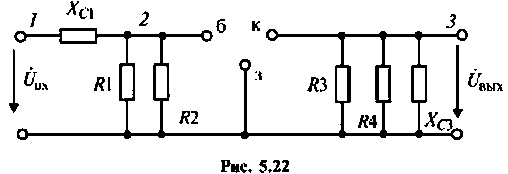
2. Выберем независимые узлы и зададим положительное направление узловых напряжений.
3. Составим матрицу проводимостей пассивной части схемы
4. Впишем матрицу проводимостей пассивной части схемы в матрицу Y-параметров транзистора, включенного по схеме с общим эмиттером
5. Рассчитаем комплексный коэффициент передачи по напряжению
Пример 5.2.6.
Рассчитать комплексный коэффициент передачи по напряжению однокаскадного транзисторного усилители (рис. 5.23) МУН. Транзистор представить схемой замещения на базе Y-параметров. Построить АЧХ усилителя в диапазоне
Дано:
Решение
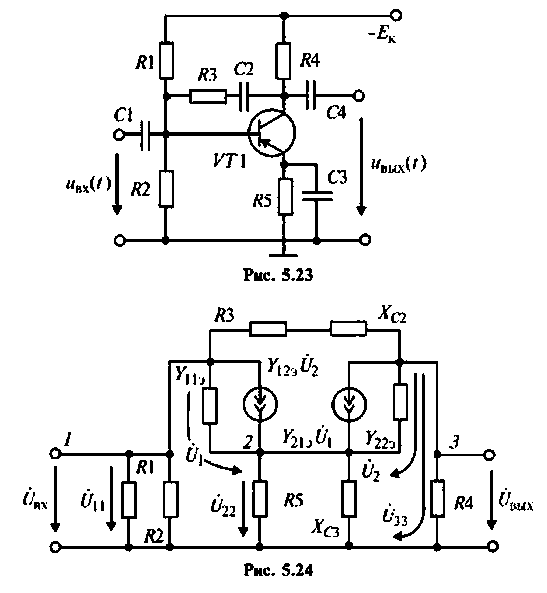
1. Составим эквивалентную комплексную схему транзисторного усилителя по переменному току (рис. 5.24).
2. Выберем независимые узлы и зададим положительное направление узловых напряжений.
3. Составим систему уравнений по МУН
4. Выразим напряжения 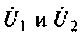
5. Подставим значения напряжений 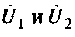
6. Сгруппируем подобные слагаемые в уравнениях (5.3):
7. Запишем матрицу проводимостей из полученной системы уравнений (5.4)
8. Подставим числовые значения и матрицу проводимостей
9. Рассчитаем комплексный коэффициент передачи по напряжению:
После подстановки и преобразований получим
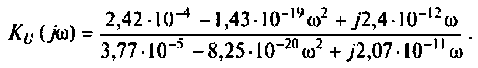
Модуль комплексного коэффициента передачи определяется выражением 
10. Рассчитаем значения модуля комплексного коэффициента передачи по напряжению и диапазоне частот
По результатам расчета построим график АЧХ и среде Mathcad (рис. 5.25).
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Линейные диаграммы
- Круговые диаграммы
- Цепи с взаимной индукцией
- Трехфазные цепи
- Нелинейные электрические цепи
- Магнитные цепи и их расчёт
- Цепи переменного тока
- Символический метод расчета цепей
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
📹 Видео
2 2 Элементы схем замещенияСкачать

3,9 Уравнения состояния АДСкачать

Классификация четырехполюсников. Системы уравнений четырехполюсниковСкачать

26.1 Эквивалентная схема трансформатора.Скачать

1 3 4 Комплексные схемы замещения идеализированных пассивных элементовСкачать

Схемы замещения и соединение источников ЭДС| Физика в техникумеСкачать

1 5 ЧетырехполюсникиСкачать



























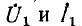
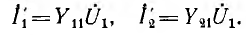
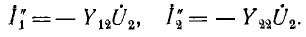

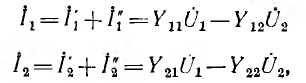
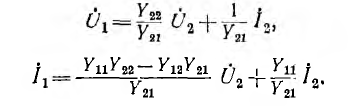
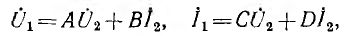
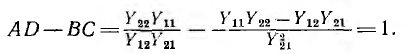
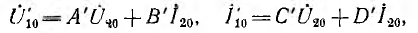
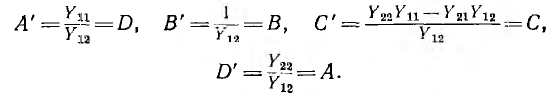
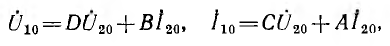
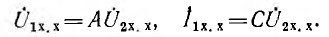

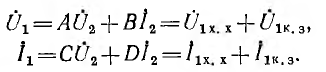
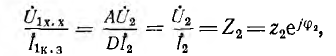
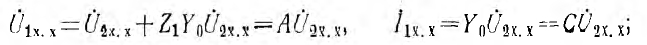
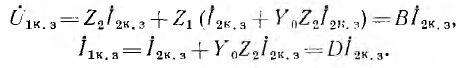
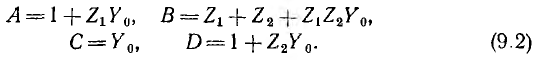
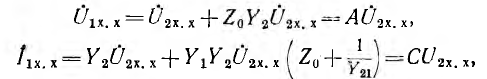
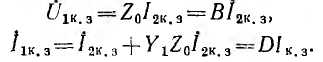
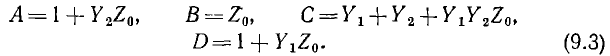
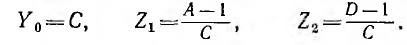
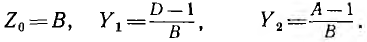
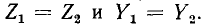
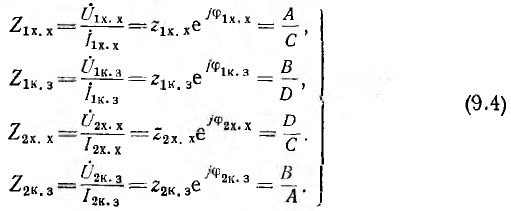
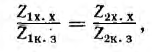
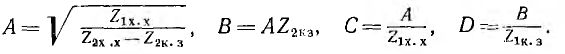
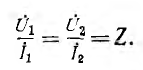
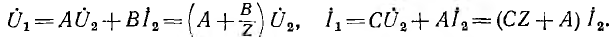
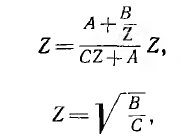

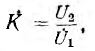
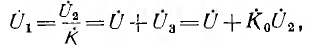
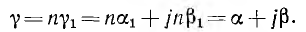
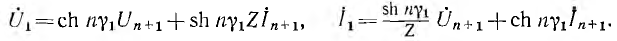
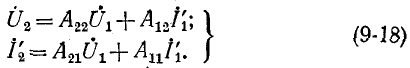
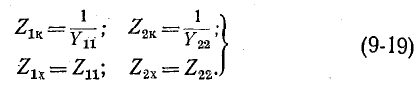
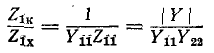
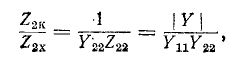

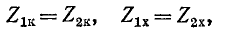

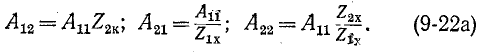
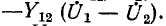
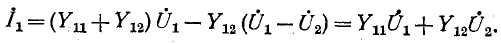
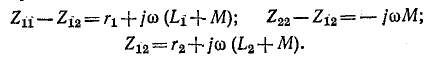
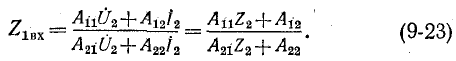
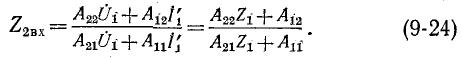
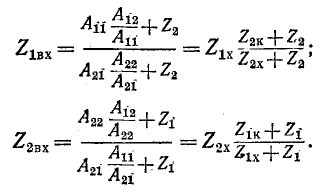
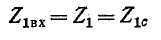
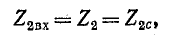
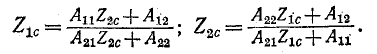
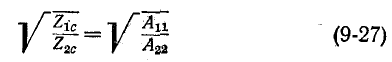
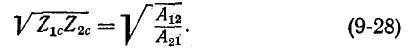
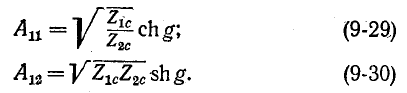
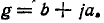
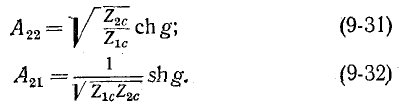
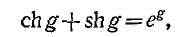
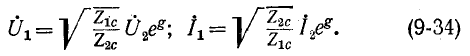
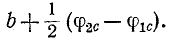
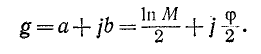
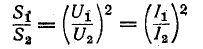
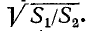
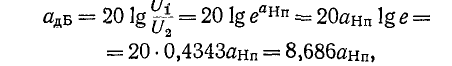
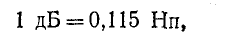
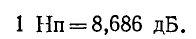
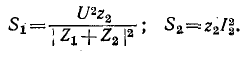
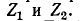
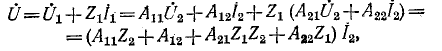
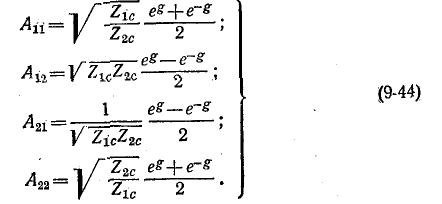
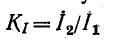
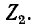
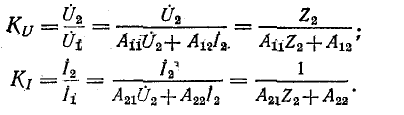
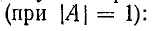
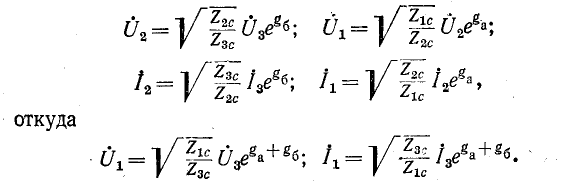
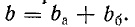
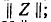
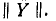 Каскадное соединение четырехполюсников (рис. 9-10). Уравнения
Каскадное соединение четырехполюсников (рис. 9-10). Уравнения